圆锥曲线“定垂轴弦”的一个有趣性质
2022-11-08 09:16山东省邹平双语学校256200姜坤崇
中学数学研究(江西) 2022年11期
山东省邹平双语学校 (256200) 姜坤崇 王 雪
我们把垂直于圆锥曲线对称轴的一条定弦称为圆锥曲线的“定垂轴弦”.关于圆锥曲线的“定垂轴弦”,笔者发现其有如下的一个有趣性质.
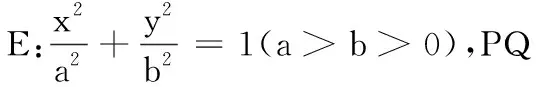

图1
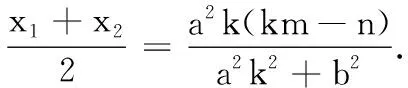
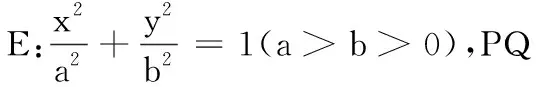
证明可仿照定理1的证明进行,这里从略.
类似地,可以证明在双曲线中有如下两个结论(证明均从略):
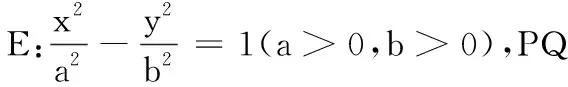
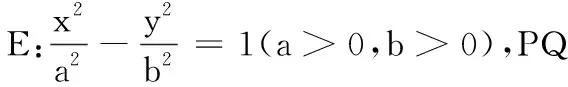
在抛物线中,亦有和椭圆、双曲线类似的如下结论:
定理5 给定抛物线E:y2=2px(p>0),PQ是过定点(m,0)(m>0)且垂直于x轴的“定垂轴弦”,设过弦PQ上的一点M(M不在x轴上)且被M平分的E的弦为AB,则过点M且垂直于AB的直线l恒过x轴上的一定点C(p+m,0).

图2
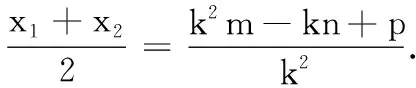
猜你喜欢
语数外学习·高中版下旬(2022年2期)2022-04-09
中学数学研究(广东)(2022年1期)2022-03-14
——阅读《能跑会跳的房子》
作文小学中年级(2020年12期)2021-01-16
——阅读《好天气和坏天气》
作文小学中年级(2020年9期)2020-09-29
中学生英语·教师版(2019年12期)2019-08-03
小学生学习指导(中年级)(2019年5期)2019-04-19
未来英才(2016年17期)2017-01-06
福建中学数学(2016年2期)2016-10-19
数学大王·低年级(2016年10期)2016-09-10
廉政瞭望(2012年1期)2012-02-11

