《数学通报》问题2603号的隔离与改进
2022-11-08 09:16:30福建省福州市书生实验学校350300李云杰
中学数学研究(江西) 2022年11期
福建省福州市书生实验学校 (350300) 李云杰
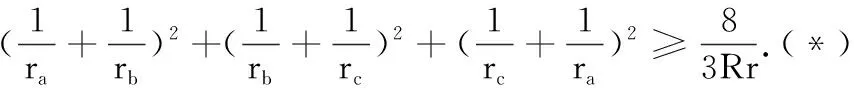
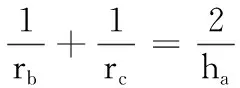
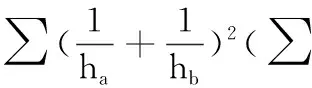
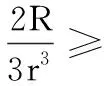
证明:按从左到右的顺序进行.
(1)第一个不等式的证明.

当R-3r≥0时,显然有(R-3r)s2+3r2(4R+r)≥0成立.当R-3r<0时,由于s2≤4R2+4Rr+3r2(Gerrestsen不等式),要证明(R-3r)s2+3r2(4R+r)≥0,只需证明(R-3r)(4R2+4Rr+3r2)+3r2(4R+r)≥0,等价于证明(R-2r)(4R2+3r2)≥0,等价于证明R≥2r,此即欧拉不等式.从而,第一个不等式得证.
(2)第二个不等式的证明.
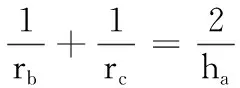
(3)第三个不等式的证明.
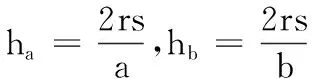
(4)第四个不等式的证明.
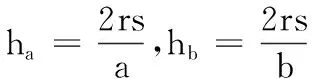
(5)第五个不等式的证明.
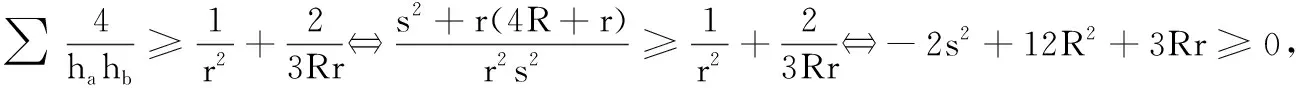
(6)第六至八个不等式的证明.
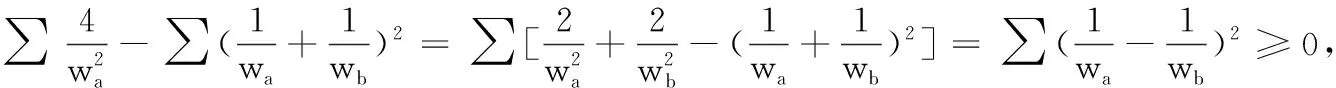
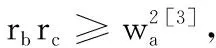
(7)第九个不等式的证明.
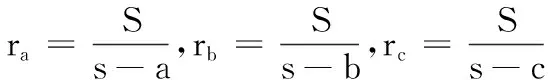
猜你喜欢
汽车观察(2022年12期)2023-01-17 02:20:42
哈哈画报(2022年1期)2022-04-19 11:27:20
车迷(2022年1期)2022-03-29 00:50:26
——福州市冯宅中心小学简介(二)
福建基础教育研究(2020年9期)2020-10-21 02:26:56
——福州市冯宅中心小学简介(一)
福建基础教育研究(2020年9期)2020-10-21 02:26:46
红土地(2019年10期)2019-10-30 03:35:06
意林·全彩Color(2019年9期)2019-10-17 02:26:06
福建基础教育研究(2019年5期)2019-05-28 08:39:49
数学小灵通·3-4年级(2017年9期)2017-10-13 08:11:04
海峡姐妹(2014年2期)2014-02-27 15:08:53

