例谈指对数混合式问题的同构解法

浙江省湖州新世纪外国语学校莲花庄校区 (313000) 孙 平

在数学解题实践过程中，同构法有着重要的作用，对于一些由指数函数、对数函数混合的问题，通过采用移项、加、减、乘、除、乘方、开方、取对数等诸多方式对函数进行变形，使其左、右两边呈现出结构相同的形式，然后重新构造函数，结合导数研究函数性质进行处理，使问题得以顺利解决.具体来说:处理同时涉及指数函数ex与对数函数lnx的相关等式或不等式问题时,往往需要灵活运用对数恒等式alogaN=N,logaaN=N的特例,即elnx=x,lnex=x．涉及到具体解题时,时常还要用到xlnx=lnx·elnx=tet(设t=lnx)，xex=ex·lnex=tlnt(设t=ex)等变式.一般而言，通过构造同构函数解决指对数混合式问题通常有以下三种基本模式，本文例析如下．

1 “和差型”模式

这种模式的解题流程呈现以下特点:

例1 已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1，求a的取值范围．

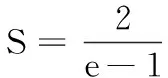
(2)由f(x)≥1可知aex-1-lnx+lna≥1，于是elna+x-1-lnx+lna≥1，则elna+x-1+lna+x-1≥lnx+x=elnx+lnx.令g(t)=et+t，则g′(t)=et+1>0，则g(t)在R上单调递增，而g(lna+x-1)≥g(lnx)，所以lna+x-1≥lnx恒成立.若lna≥lnx-x+1恒成立，只需lna≥(lnx-x+1)max.

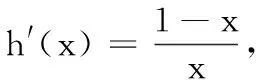
评注：本题第(2)问先运用对数恒等式,对原不等式变形,然后通过移项、将不等式的两边都加上x,使不等式的两边出现同构的形式,进而构造函数,利用导数研究函数的单调性,再将不等式转化,分离参数后二次构造函数,利用“最值法”求出a的取值范围．其中将不等式变形出相应的同构式是求解本题的关键．当然，我们还可以通过aex-1-lnx+lna≥1得到elna+x-1+lnelna+x-1≥x+lnx，然后构造g(t)=t+lnt也可以使问题获解．

2 “乘积型”模式

这种模式的解题流程呈现以下特点:

例2 对任意x>0,不等式2ae2x-lnx+lna≥0恒成立,则实数a的最小值为( ).

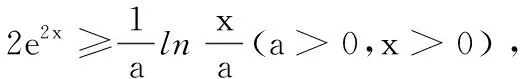
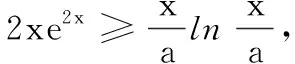
3“作商型”模式

这种模式的解题流程呈现以下特点:

例3 证明: 当x>0时，恒有(ex-1)ln(x+1)>x2．

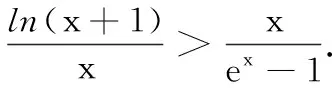
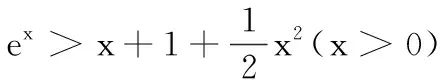
“同构”解题策略，即通过分析代数式的结构特征，从而发现式子结构中蕴藏的同型与共性，并提取相同或相似的结构与模型并予以构造，揭示式子间的内在联系，继而利用同型同构后的模型性质予以解题的数学方法.显然以上运用“同构”策略解决指对数混合式问题的过程及其模式可以说是“提纲挈领、言简意赅”.