“教-学-评一致性”视角下的作业设计实践与反思*

浙江省安吉县高级中学 (313300) 韩志刚浙江省安吉县教科研中心 (313300) 姚文建

一、问题提出

当下，“苦教苦学”教学观的偏移造成作业观的错位，即教师布置作业时奉行“多多益善”，将学生推进题海，学生作业时间长，思考少，作业能引发的学习活动变成了机械训练.这种现象反映了师生缺乏对“教-学-评一致性”的思考.崔允漷及雷浩教授在美国著名教育评价专家韦伯(Webb，N．L．)工作的基础上，将“教-学-评一致性”定义为在整个课堂教学系统中教师的教、学生的学和对学生学习的评价三个因素的协调配合的程度.[1]清晰的目标是“教-学-评一致性”的核心.判断教-学-评是否一致的依据是教师的教、学生的学与教学评价是否都是围绕共同的目标展开.教师能根据教学目标，设计相应的教学活动和作业任务，针对学情反馈给出适当的评价.[2]这也是教师的一项教学基本功.一般地，人们研究“教-学-评一致性”，更多将视角放在教学上，解决“有效教学”的问题.本文试图以围绕和促进“教-学-评一致性”的作业设计为研究载体，探究新课程理念的一种落实途径.

二、作业设计案例

科学合理的作业设计能有效的提升作业质量，从而减轻学生学业负担.笔者以“数学归纳法(第1课时)”为例，在新课程理念下进行了作业设计探究，以此促进“教-学-评一致性”.

(一)目标确定

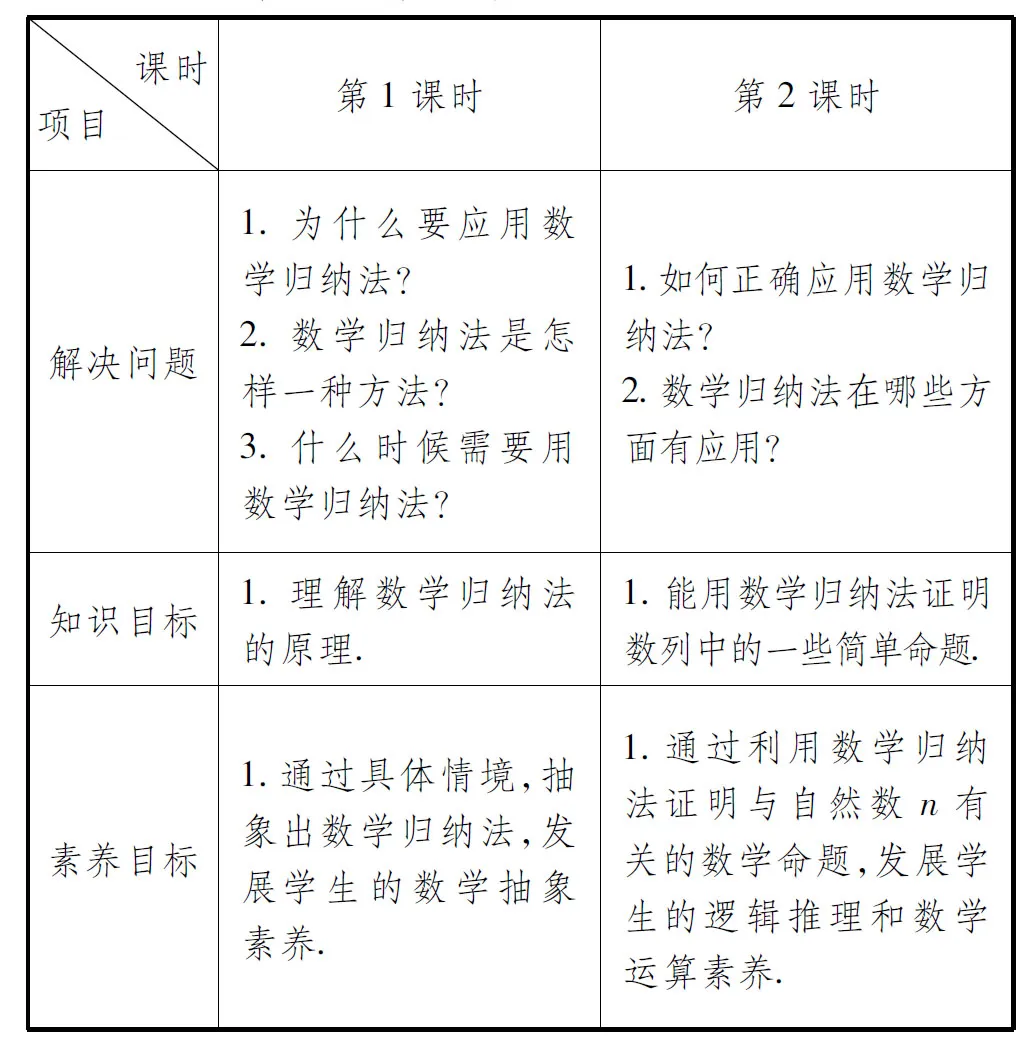
一节课目标的确定要考虑以下几组关系：单元目标与本课目标之间整体与部分的关系，素养目标与知识目标之间隐形和显性的关系，上级目标与下级目标之间逐渐可视化的统领关系.现将《4.4数学归纳法》这一节作为一个单元进行分析，分解为2课时.

1.本单元的地位

教科书将数学归纳法的应用置于“数列”的整体框架之中，适度加强“观察-归纳-猜想-证明”的探索性思维方式的渗透.学习一个方法，都会面临以下三个问题：为什么要学习这个方法？这个方法是怎样的？这个方法怎么运用？因此本单元要从数列中碰到的困难引出先猜后证的思想，从而引出数学归纳法.而本单元的应用要延伸到与正整数有关命题的证明，含有等式和不等式.

2.本单元知识结构框图

3.单元设计理念下本课目标的确定

3.1 单元目标描述

核心知识目标核心素养目标1.理解数学归纳法的原理.2.能用数学归纳法证明数列中的一些简单命题.1.通过具体情境,抽象出数学归纳法,发展学生的数学抽象和逻辑推理素养.2.通过利用数学归纳法证明与自然数n有关的数学命题,发展学生的逻辑推理和数学运算素养.

3.2 单元目标分解

3.3 本课目标的可视化

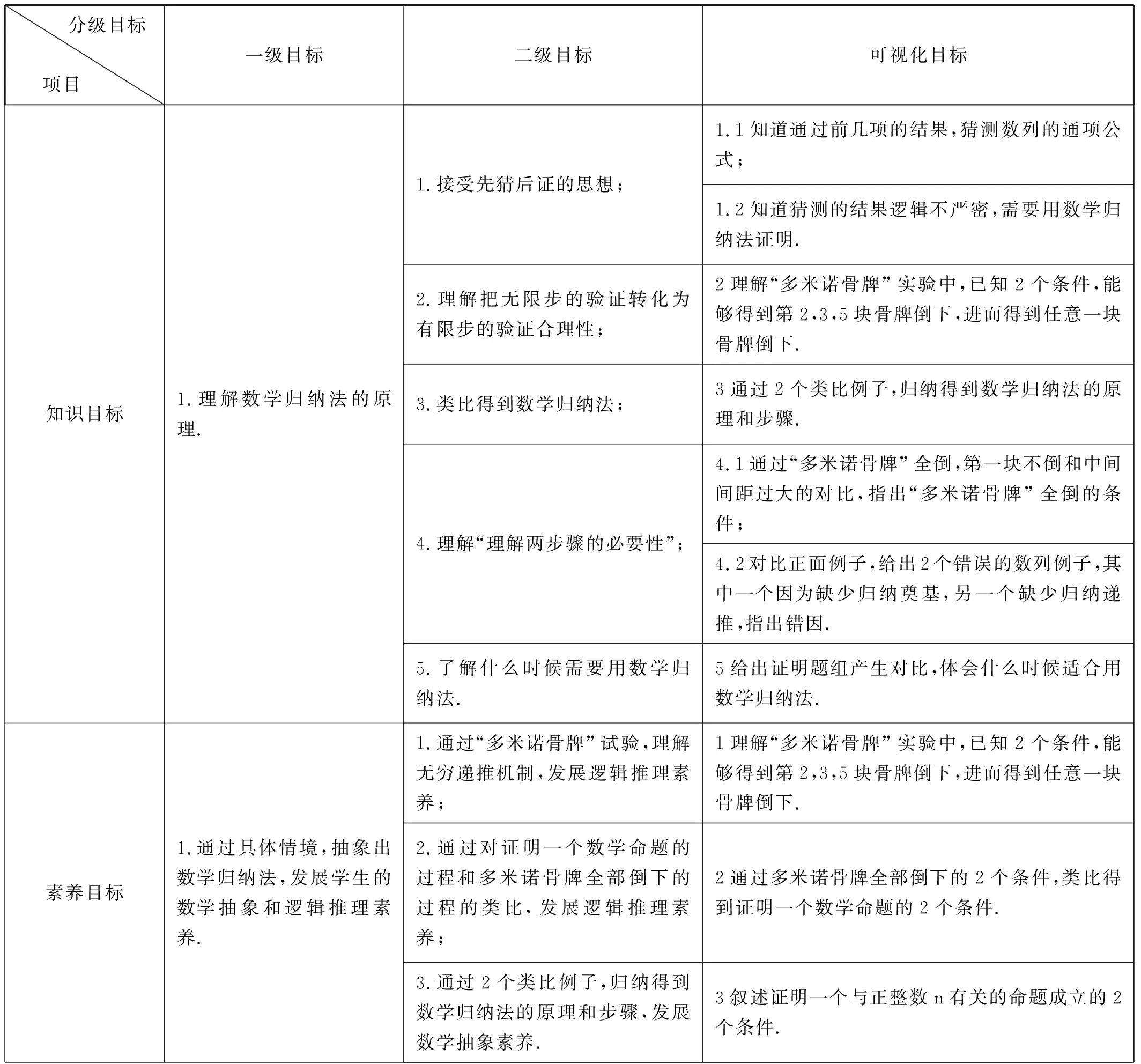
分级目标项目 一级目标二级目标可视化目标知识目标1.理解数学归纳法的原理.1.接受先猜后证的思想;2.理解把无限步的验证转化为有限步的验证合理性;3.类比得到数学归纳法;4.理解“理解两步骤的必要性”;5.了解什么时候需要用数学归纳法.1.1知道通过前几项的结果,猜测数列的通项公式;1.2知道猜测的结果逻辑不严密,需要用数学归纳法证明.2理解“多米诺骨牌”实验中,已知2个条件,能够得到第2,3,5块骨牌倒下,进而得到任意一块骨牌倒下.3通过2个类比例子,归纳得到数学归纳法的原理和步骤.4.1通过“多米诺骨牌”全倒,第一块不倒和中间间距过大的对比,指出“多米诺骨牌”全倒的条件;4.2对比正面例子,给出2个错误的数列例子,其中一个因为缺少归纳奠基,另一个缺少归纳递推,指出错因.5给出证明题组产生对比,体会什么时候适合用数学归纳法.素养目标1.通过具体情境,抽象出数学归纳法,发展学生的数学抽象和逻辑推理素养.1.通过“多米诺骨牌”试验,理解无穷递推机制,发展逻辑推理素养;1理解“多米诺骨牌”实验中,已知2个条件,能够得到第2,3,5块骨牌倒下,进而得到任意一块骨牌倒下.2.通过对证明一个数学命题的过程和多米诺骨牌全部倒下的过程的类比,发展逻辑推理素养;2通过多米诺骨牌全部倒下的2个条件,类比得到证明一个数学命题的2个条件.3.通过2个类比例子,归纳得到数学归纳法的原理和步骤,发展数学抽象素养.3叙述证明一个与正整数n有关的命题成立的2个条件.

(二)作业生成

根据以上一级和二级目标，制定课堂设计和作业设计；根据可视化目标，设计课堂师生活动和选择作业具体题目.

1.课堂设计流程

为了直观体现“教-学-评一致性”，先将课堂主要活动流程设计展现如下：

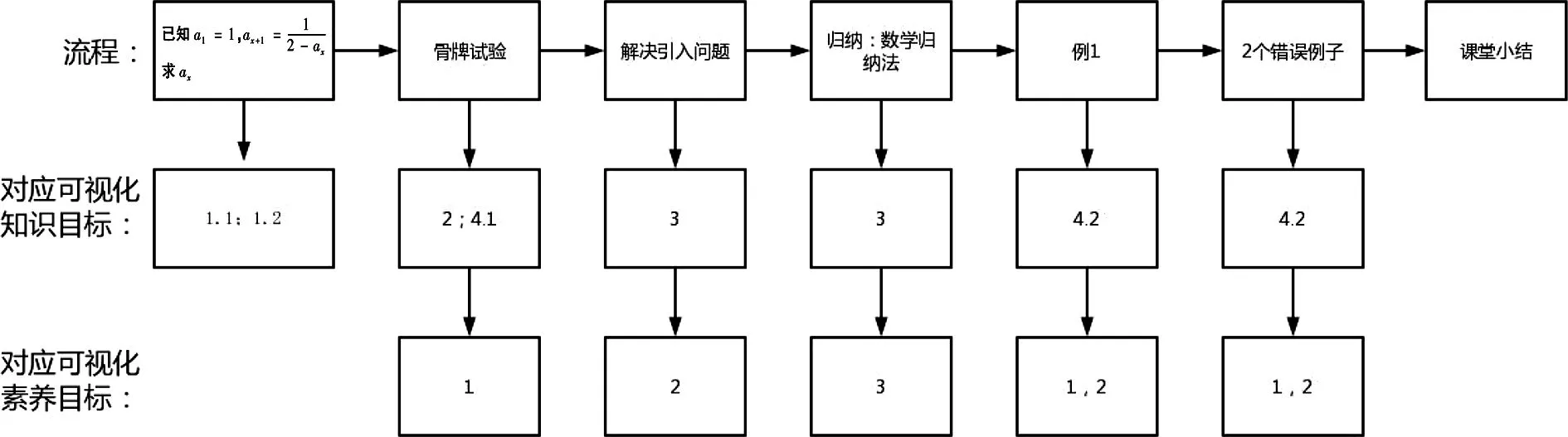
2.作业设计

作业设计主要依据为可视化目标，同时在知识目标达成层面要考虑题目的不同难度选择，在素养目标达成层面要考虑题目的不同情境选择.选出题目如下：

1．现有竖放的若干多米诺骨牌，满足第k块骨牌倒下一定导致第k+1块骨牌倒下(k∈N*)，现已知第5块骨牌倒下，那么可推导出( ).

A．第6块骨牌不倒下 B．第6块骨牌倒下

C．第4块骨牌不倒下 D．第4块骨牌倒下

2．一个与正整数n有关的命题，当n=2时命题成立，且由n=k时命题成立可以推得n=k+2时命题也成立，则( ).

A．该命题对于n>2的自然数n都成立

B．该命题对于所有的正偶数都成立

C．该命题何时成立与k取值无关

D．以上答案都不对

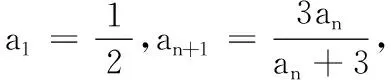
4．用数学归纳法证明1+2+22+…+2n-1=2n-1(n∈N*)的过程如下：

(1)当n=1时，左边=1，右边=21-1=1，等式成立．

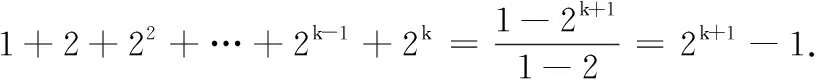
5.以下的2个问题，你能解决吗？哪些你需要用到数学归纳法？

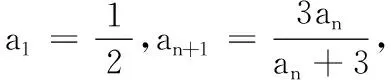
(1)你是否用到数学归纳法？是；否(请在你选择的办法上划“√”)，解决办法为.

(2)你是否用到数学归纳法？是；否(请在你选择的办法上划“√”)，解决办法为.

6.已知首项为a1，公比为q的等比数列{an}.

(1)根据等比数列的定义，用数学归纳法证明{an}的通项公式是an=a1qn-1；

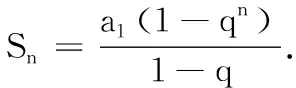
3.作业设计说明

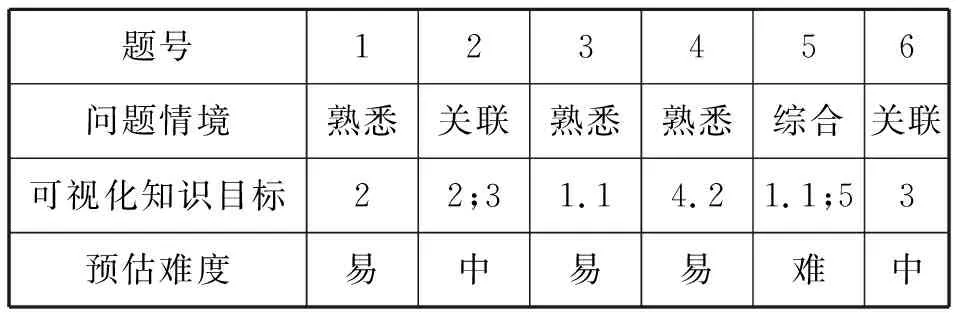
题号123456问题情境熟悉关联熟悉熟悉综合关联可视化知识目标22;31.14.21.1;53预估难度易中易易难中

说明：①熟悉情境、关联情境、综合情境分别简称为熟悉、关联、综合；②1，3，4为课上讲的同类问题，为熟悉情境；2由课中的连续变为跳跃，6由课中的等差变为等比，为关联情境；5由指向性的证明问题转变为先猜后证，且涉及到课中未涉及的策略选择，为综合情境.

(三)作业反馈及评价

1.学情反馈

收集了一个班的作业情况，该班属于县域最好学校，处于学校的平均水平，共43人.信息如下：

题号123456问题情境熟悉关联熟悉熟悉综合关联可视化知识目标22;31.14.21.1;53预估难度易中易易难中

2.多维度评价

2.1知识目标达成度

以二级目标每一项的正确率体现该项的达成度，共5项，正确率如下：

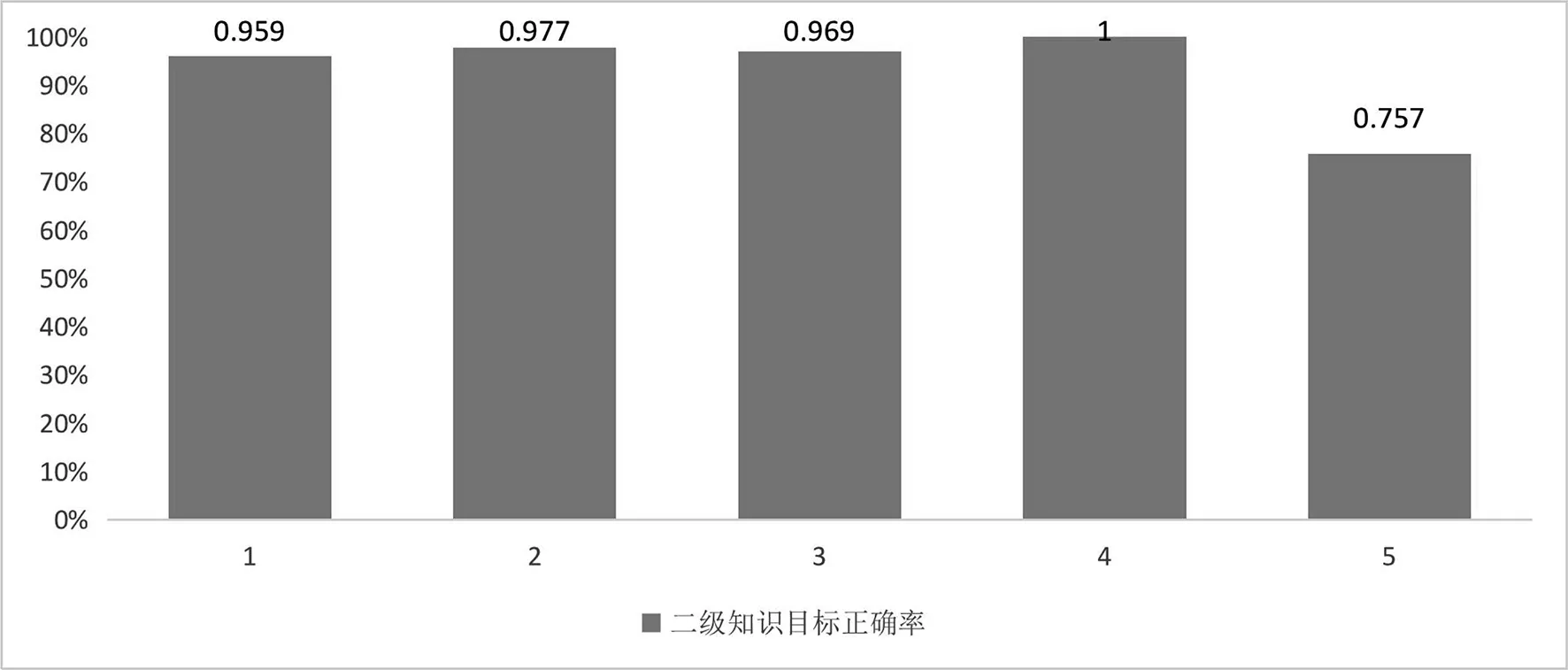
2.2素养目标水平

数学核心素养需要检测学生在熟悉情境、关联情境、综合情境中的真实反应，以区分学生的核心素养水平.以下统计学生在熟悉情境、关联情境、综合情境问题下的作业正确率，体现其素养目标水平.

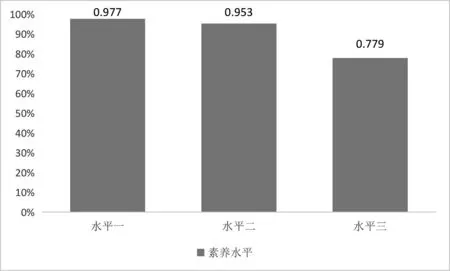
说明：素养水平一、水平二、水平三分别指在熟悉情境、关联情境、综合情境下的学习水平.

从以上两方面分析来看，最值得讲评的是第5题.事实上，第5题的价值也得到了学生的认可，调查结果显示第5题在“哪个题对你理解本课有帮助”评选中排第二.

3.讲评与巩固

3.1讲评目的与策略

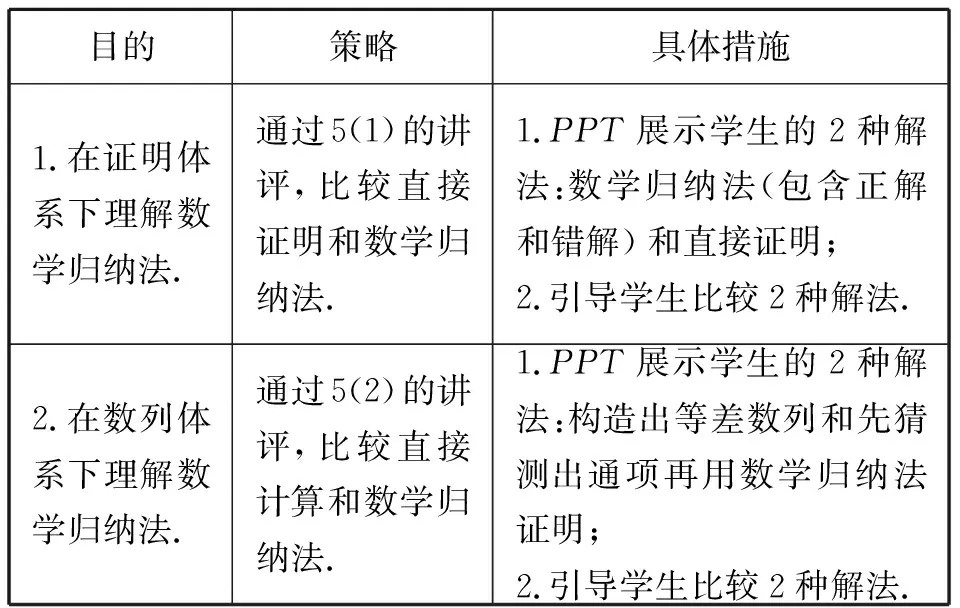
目的策略具体措施1.在证明体系下理解数学归纳法.通过5(1)的讲评,比较直接证明和数学归纳法.1.PPT展示学生的2种解法:数学归纳法(包含正解和错解)和直接证明;2.引导学生比较2种解法.2.在数列体系下理解数学归纳法.通过5(2)的讲评,比较直接计算和数学归纳法.1.PPT展示学生的2种解法:构造出等差数列和先猜测出通项再用数学归纳法证明;2.引导学生比较2种解法.

3.2巩固与效果

在2天后的一次数列综合检测中，布置了以下二道题：

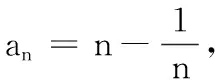
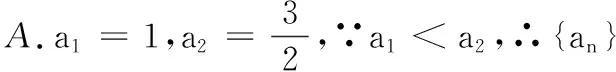
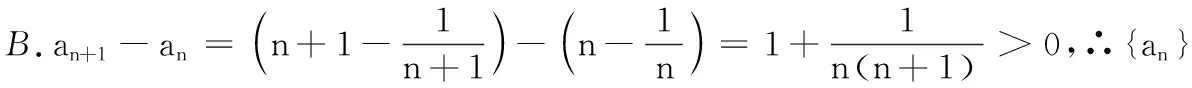
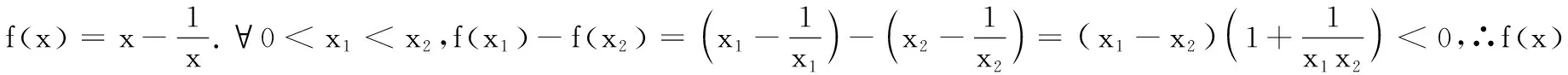
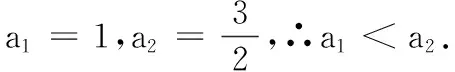
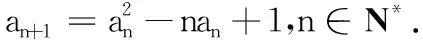
(1)当a1=2时，求a2，a3的值并进一步求an；

(2)当a1≥3时，证明：对所有的n∈N*，有an≥n+2.

统计出答题情况如下：

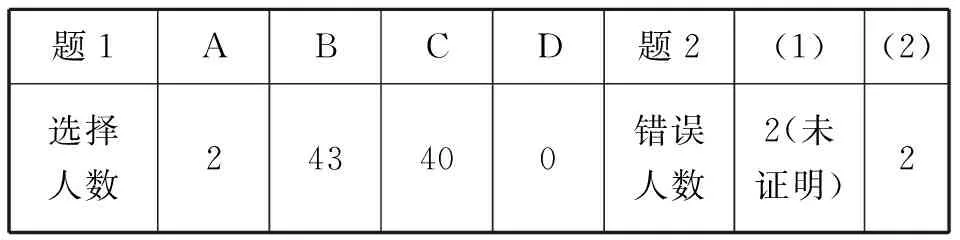
题1ABCD题2(1)(2)选择人数243400错误人数2(未证明)2

三、作业设计反思

科学的作业设计应该能串联起教师的教、学生的学及对教学效果的评价，使其协调统一.并且应有如下特征：

1.作业设计指向教学检测

作为教师，应该始终带有疑问“我课上讲的东西学生学会了吗？”.如此，则应该把作业设计作为解决这一疑问的工具.在教-学-评统一的目标下，选择能够有效检测的问题.无疑，其中最关键的是共享目标的逐级细化，直至分解出可视化目标.

2.作业设计指引学习方向

作为学生，希望明白“我要到哪里去”，作业作为主要的学习载体，和课堂教学一起担负着指明学习方向的任务.科学的作业设计要指明知识的广度和深度，即要掌握哪些知识点，其中核心知识点是什么，每个知识点要掌握到什么程度.同时要蕴含关键技能和思维方法，作为暗线指引学生要掌握的技能和方法.

3.作业设计指向多元评价

现代教育的实施越来越依赖于评价，以评价促成长.教师需要在学生的学习过程中对其学习水平进行评价，以帮助学生认清差距，从而明确学习方向.《普通高中数学课程标准(2017版2020年修订)》指出评价应突出过程性评价和评价的多元性.科学的作业设计应该隐含有评价的多元指标：核心知识、关键技能、思想方法和素养水平.

总之，作业的选材要注重情景化背景、课时作业的评价不止要关注知识性评价，更要关注核心素养评价.新课程理念关注的单元设计、分层作业、情境作业能分别在指向教学检测、指明学习方向、指向多元评价方面起到关键性作用.真正实现在作业层面促进“教-学-评一致性”，提升作业质量，减轻学习负担.