陆地高精度重力观测数据的应用研究进展

韩建成，陈 石*，李红蕾，张 贝，卢红艳，侍 文，徐伟民，贾路路

1中国地震局地球物理研究所，北京100081

2北京白家疃地球科学国家野外科学观测研究站，北京100095

0 引言

重力场是地球的基本物理场，其静态和动态（时变）特征反映了地球内部和表层物质的分布变化和运动状态.重力场观测数据既可为地球内部结构和地球动力学等研究提供基础观测信息（胡明城，2003；许厚泽等，2012；孙和平等，2017），也在经济建设和国家安全等领域发挥重要作用，广泛应用于矿产资源勘探、水资源变化监测、地震活动性分析以及国防军事等领域（Hinze et al.,2013；祝意青,2013a；陈石等,2015；Van Camp et al.,2017；胡敏章等,2019；姚宜斌等,2020）.

陆地重力观测在陆地表面固定测点设置重力仪进行单次、重复或连续的重力测量工作，是获取地球重力场数据的主要手段之一（刘经南等,2000;Niebauer,2015）.陆地重力观测采用的重力仪有两种，分别是相对重力仪和绝对重力仪，其中前者测定重力加速度的相对差值，后者测定的是绝对重力加速度值.实用型高精度重力仪的发展经历了一个长期过程，目前可实现μGal量级（1 μGal= 1×10−8m/s2）陆地重力测量.1970年代，美国LaCoste Romberg公司推出的金属弹簧相对重力仪将陆地重力观测精度由mGal量级（1 mGal=1×10−5m/s2）提升到几十μGal量级（LaCoste Romberg G型标称精度优于20μGal,Crossley et al.,2013），并且便于移动，被广泛应用于大范围重力测量（贾民育，2000）.随着电子机械技术的迅猛发展，高精度绝对重力仪和超导重力仪也逐渐实现了商业化和便携化（Niebauer, 2015），如美国Micro-g公司生产的FG5型绝对重力仪，观测精度约为2μGal（Francis and van Dam,2005;Niebauer et al.,2005;Niebauer,2015）；美国GWR公司生产的OSG（observatory superconducting gravimeter）标准型超导重力仪的观测精度可达0.02μGal，可移动iGrav轻便型超导重力仪的观测精度可达0.05μGal（Crossley et al.,2013）.

根据测量方式的不同，陆地重力观测得到的数据主要有两种，一种是静态的重力异常（以下称陆地重力异常数据）；另一种是重力场随时间的变化（以下称陆地时变重力数据）.陆地重力观测具有距离场源近和测量精度高的特点，观测结果包含丰富的高频信息（Saleh et al.,2012;Bomfim et al.,2013;陈晓东等,2020）.其中，陆地重力异常数据对研究地球内部结构和密度分布有显著贡献（Torge,1989; 马宗晋等,2006;Hinze et al.,2013）；同时，陆地时变重力数据的空间分辨率高、测点可重复性强，适于分析区域性、近地表的质量和应力变化特征（Abe et al.,2012;Kennedy et al.,2014; 许才军和尹智,2014;Chen et al., 2016;Van Camp et al.,2017;陈石等,2018），长期观测资料也为探测地球内部微弱动力学信号提供了新的数据支持（孙和平等，2017）.

随着陆地重力观测技术的迅速发展、观测网络的逐渐完善以及观测数据的不断积累，近年来相关领域基于陆地重力观测的研究成果不断涌现.本文将简要梳理和介绍陆地重力观测在大地测量学和地球物理学（地球内部结构、地球动力学、水资源监测以及地震预测）领域的研究工作.

1 陆地静态重力数据的应用

本文中的陆地静态重力数据，是指地表观测获得的重力异常数据，主要包括：自由空气重力异常（free-air gravity anomaly,FGA）和布格重力异常（Bouguer gravity anomaly,BGA）.地面重力数据经观测改正后，再做空间改正可获得自由空气重力异常FGA.FGA与地形相关性强，对FGA进一步做层间改正和地形改正，可获得适于反映地下密度不均匀性的完全布格重力异常（郭俊义,2001;Hofmann-Wellenhof and Moritz,2006;Fullea et al.,2008;Pašteka et al.,2017）.FGA和BGA在全球变化范围从负几百到近一千 mGal（Balmino et al.,2012）.下文如无特别说明，BGA均指完全布格重力异常.

1.1 构建重力场和大地水准面模型

陆地实测重力异常在物理大地测量学领域的一个重要应用就是构建（精化）重力场及大地水准面模型（李建成等,2003；Hofmann-Wellenhof and Moritz,2006；韩建成,2012）.目前得到广泛应用的EGM2008全球重力场模型（完整展开到2 190阶，2 159次），空间分辨率5′×5′，在构建时采用了陆地重力、卫星重力和卫星测高等多源数据，其中全球地面测量FGA数据约130万（Pavlis et al.,2012,2013）.EGM2008较其上一代全球重力场模型EGM96（完整展开到360阶次）在空间分辨率和精度上都有了巨大提升，在我国大陆地区的整体精度约10 mGal（章传银等，2009）.空间分辨率达2′×2′的XGM2019e全球重力场模型（完整展开到5 400阶次）同样采用多源数据，其中地面测量FGA数据约180万（Zingerle et al.,2020）.XGM2019e较EGM2008在空间分辨率和精度上均有提升，且该模型未来会继续更新（Wan et al., 2020;Zingerle et al.,2020）.目前公开发布的全球地球重力场模型都可在ICGEM（international centre for global Earth models）官方网站（http://icgem.gfz-potsdam.de/）上找到（Ince et al.,2019），官网模型信息页面给出了各模型所用数据源，除仅利用卫星重力数据解算的模型外，基本都采用了陆地重力数据.基于某一地区所测陆地重力数据可以精化区域（局部）重力场模型，如Denker（2013）、Bucha等（2016）和吴怿昊等（2016）.

陆地重力异常数据对建立高精度、高分辨率大地水准面模型至关重要.我国2′×2′ 重力似大地水准面CNGG2011在计算中采用了超过100万点的陆地重力异常数据（李建成，2012）.2017年由国际大地测量协会（International Association of Geodesy）的两个工作组联合发起并组织了“Colorado geoid experiment”（Claessens and Filmer,2020;Jiang et al.,2020;Wang et al.,2020;Işık et al.,2021），美国NGS（National Geodetic Survey）为此实验提供了Colorado地区的多种数据，其中包括近6万点陆地重力观测数据.Hwang等（2020）确定中国台湾区域30″×30″大地水准面时，采用了6 000多点陆地重力异常数据.在2019～2020年珠峰高程测量工作中，建立作为珠峰区域高程基准的重力似大地水准面模型使用了8 000多点陆地重力异常数据（党亚民等，2021）.

陆地重力观测目前仍存在很多数据稀疏区和空白区，以全球来看，EGM2008收集的陆地重力数据约有12% 的数据空白区，主要集中在非洲、南美洲和南极洲（Pavlis et al.,2012）；以我国来看，西部重力数据稀疏，青藏高原存在大面积空白区（李建成，2012）.在重力稀疏区和空白区，重力场和大地水准面模型精度受到明显限制.以我国CNGG2011大地水准面为例，精度评估表明其平均精度为0.13 m，在东部陆地重力数据较为密集的18省平均精度为0.07 m，西部陆地重力较稀疏的9省精度为0.14 m，而存在数据空白区的西藏，精度为0.22 m（李建成，2012）.如何克服陆地重力稀疏区和空白区的影响，是进一步精化重力场和大地水准面模型要面临的主要问题.

1.2 建立地壳物性结构模型

陆地重力异常数据 BGA反映的物质密度分布不均匀性是重力学关注的重要信息.重力反演方法对横向密度变化敏感，是探测地壳密度构造的有效手段之一（Nabighian et al.,2005;Hinze et al.,2013）.BGA的精度受重力测量和各项改正误差的影响.利用BGA研究区域尺度（比例尺大于1:100万）的地壳构造和密度分布等问题时，《区域重力调查规范（DZ/T 0082—2006）》（区域重力调查规范编写组，2006）建议陆地重力测量精度不低于0.4 mGal，BGA精度不低于1 mGal.国外相关研究并无对BGA精度的明确建议，例如Hinze等（2013）仅建议进行重力勘探等研究时陆地重力测量精度应满足0.01～1 mGal.

由于BGA是地球内部密度不均匀和界面起伏的综合反映，需对BGA数据进行处理和分析，分离出岩石圈密度结构产生的重力效应，然后构建重力异常与密度模型的对应关系，最终通过一定算法估计最优的模型参数（王新胜，2012；石磊等，2015；李红蕾等，2017；雷晓东等，2021）.需要指出的是，由于反演问题固有的多解性，数学意义上最优的反演结果可能与真实情形并不相符，此时加入先验约束条件可以改善重力反演的效果（Li and Oldenburg,1998;楼海,2001;陈石等,2014;申重阳等,2015;张晰等,2016;李红蕾等,2021）.除单独利用重力异常进行反演外，还可引入重力梯度数据以进一步提高反演结果的准确性和分辨率（Zhdanov et al.,2004;秦朋波和黄大年,2016;李红蕾等,2017;Tian et al.,2021）.

重力反演方法还适合与其他地球物理学方法（如地震学和大地电磁等方法）进行联合反演，可有效提高反演精度并降低多解性.Maceira和Ammon（2009）发展了一种基于面波与BGA重力异常的联合反演方法，基于此方法获得了塔里木盆地和准噶尔盆地的地壳和上地幔三维S波速度模型.该模型提高了20 km浅层地质结构的分辨率，进而发现塔里木盆地东部和西部的地壳和上地幔S速度存在差异.王新胜等（2013）利用BGA和地震波数据反演了青藏高原东北缘三维密度结构，发现该区域中上地壳存在有利于地震孕育和发生的高低密度异常相间分布.郭震等（2015）利用面波和BGA联合反演方法得到了山西断陷带地壳三维S波速度结构，结果显示该区域上地壳的速度结构与地表地质构造具有较强关联性.Moorkamp等（2011）提出了一个用于地震、大地电磁和重力数据的三维联合反演框架，并利用模拟实验分析了联合反演中各物理参数的不同耦合方法.国内外其他学者也开展了引入重力的地壳密度结构联合反演，取得了一系列研究成果（Bailey et al.,2012;索奎等,2015;Syracuse et al.,2016;Zhao et al.,2018;Afonso et al.,2019;李海龙等,2020;李红蕾等,2021）.

重力反演或联合反演所采用的BGA数据，其计算需要已知大地水准面以上的物质密度.BGA由FGA数据扣去层间改正和地形改正得到，FGA仅与点位高程和纬度相关，但层间改正和地形改正与大地水准面和地表之间的物质密度分布密切相关.目前一般将此密度取为地壳的平均密度，即2.67 g/cm3.当研究区域较大，尤其是跨越多个构造区时，近地表的岩石密度不能简单用地壳密度平均值代替.许多学者提出了基于FGA估计近地表岩石密度的方法和技术（Murata,1993;Nawa et al., 1997;牛源源等,2019）.其中，牛源源等（2019）提出的基于FGA和贝叶斯分析的剖面近地表岩石密度估计方法，在获得较可靠的近地表岩石密度的同时，给出光滑连续分布的BGA.在我国云南地区的应用表明，该方法所估计的地表浅层密度分布与该地区物性资料及地质特征较为吻合.上述工作表明，通过地表重力测量能获得较可靠的近地表岩层参考密度信息，这对于构建浅层地壳密度模型以及精化地壳模型都具有重要意义.例如在我国川滇地区，目前已积累大量μGal级精度的重力探测剖面数据，若能利用更可靠的浅层密度分布来计算BGA，将会为地壳密度结构反演提供更准确的约束，从而获得更优的反演结果.

1.3 反演Moho界面形态

Moho面地球内部最重要的分界面之一，其形态特征与地壳上地幔的密度分布和均衡状态关系密切（冯锐，1985）.应用BGA数据反演Moho面形态，迄今已有大量研究（黄建平等,2006;Shin et al.,2007;Sjöberg and Bagherbandi, 2011;Tenzer and Chen,2014;吴招才等, 2017;鲁宝亮等,2018;王鑫等,2020;张杰等,2020）.此外，也有学者采用重力梯度数据反演Moho面形态（Ye et al.,2016;Chen,2017）.与反演地壳密度结构相似，以地震学方法给出的Moho面起伏作为约束，可获得更优的反演结果（郭良辉等,2012;陈石等,2015;张杰等,2020）.

值得指出的是，将基于BGA反演得到的地壳厚度（Moho面深度与地表高程之和）与基于均衡理论给出的均衡状态下的地壳厚度进行对比，二者差异可反映研究区域构造单元的均衡状态，为分析复杂的深部动力学过程提供重要参考. 王谦身等（2009）研究了四川盆地和龙门山造山带的Airy均衡重力异常，发现成都平原和川西山区均处于较均衡状态、龙门山地区处于不均衡状态，这一结果反映出龙门山断裂体系深部物质的强烈交换与转移，表明该区域存在发生构造运动的趋势背景.对于龙门山区域的上述不均衡状态，张永谦等（2010）、Fu等（2014）和付广裕等（2018）分别进行了验证，得出了与王谦身等（2009）一致的结论.

1.4 估计岩石圈有效弹性厚度

岩石圈有效弹性厚度（effective elastic thickness,Te）是表征岩石圈力学强度的一个定量指标（Forsyth,1985）.定义一个覆盖在非黏性流体之上的弹性板，其在相同载荷下可产生与真实岩石圈相同的弯曲，则该弹性板的厚度即Te（Burov and Diament, 1995;郑勇等, 2012）.Te可反映岩石圈在地质时间尺度的长期载荷作用下抵抗变形的能力（Chen et al.,2013;胡敏章等,2015），Te越大意味着岩石圈抵抗变形的能力越强，即越难发生挠曲变形；反之，岩石圈则越易发生挠曲.对于本文关注的陆地区域，通过估计不同构造和地质演化单元的Te，可为认识大陆岩石圈的长期变形、理解构造运动（如克拉通破坏和青藏高原隆升等）的动力学机制研究提供参考（陈石等,2011,2013;胡敏章等,2020;Shi et al.,2020;杨光亮等,2020;侍文等,2021）.

岩石圈在上部地形负载作用下发生挠曲变形的直接体现是引起重力异常，所以重力异常和地形数据成为估计Te的理想数据.目前基于重力异常和地形数据估计陆地区域Te比较常用的是谱方法（Kirby,2014;胡敏章等,2020），如BGA-地形相干性方法（Forsyth,1985;Pérez-Gussinyé et al.,2004;Chen et al.2013;李永东等,2013）、FGA-地形导纳法等（陈石等,2011;佘雅文等,2018;付广裕和王振宇,2020）、Moho地形导纳法（杨亭等,2013），分别采用导纳法和相干性方法（Pérez-Gussinyé et al.,2009;Chen B et al.,2018）以及导纳法和相干性方法联合反演（Audet,2019;Lu et al.,2020;Shi et al.,2020）.针对谱方法中存在的频率泄露问题，Simons等（2000）以及Kirby和Swain（2011）分别提出了基于多窗分析和Fan小波分析的改进方法.除谱方法外，部分学者通过直接求解岩石圈在地形载荷作用下发生挠曲形变的偏微分方程来计算Te，如空间域的有限差分法（Jordan and Watts,2005;姜效典等,2014;胡敏章等,2020）.

目前对于中国大陆地区Te的计算，由于所用重力数据、处理过程和估计算法上的不同，不同研究给出的Te存在较大差异，并且所得结果的空间分辨率较低，普遍采用的谱方法也不利于对Te的横向变化特征展开研究（胡敏章等，2020）.还需指出的是，目前中国区域Te计算大多基于重力场模型数据计算，缺乏地表实测重力异常的约束；如果采用基于地表实测重力的BGA或FGA数据来估计Te，预期可提高估计精度，为基于Te的地球物理解释和应用提供更加精确可靠的数据支持.

2 陆地时变重力数据的应用

构成地球系统的大气、海洋、地幔和地核（液态外核与固体内核）等圈层，其内部物质在日月等天体引力及各种构造活动的作用下不停地迁移运动，导致地球重力场产生潮汐和非潮汐变化（孙和平等，2017）.图1给出了不同周期、振幅特点的潮汐和非潮汐重力场信号时频特征（Crossley et al.,2013）.其中，地壳长期形变和地震过程等与地壳内部变形相关的非潮汐时变信号多具有低频特征，量级约10μGal甚至更小.由于量级微小，重力场时变信号的观测依赖于高精度重力仪的革新.

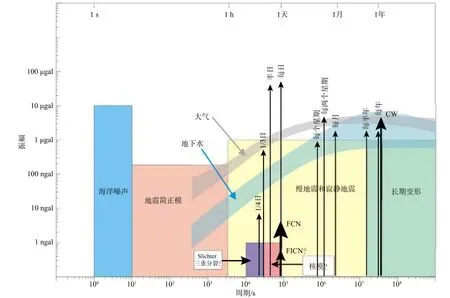
图1 与地面重力变化相关的地球内外部过程示意图（修改自Crossley et al.,2013）Fig.1 A schematic map showing various contributions from Earth's internal or external processes to the time-varying terrestrial gravity measurements (modified from Crossley et al.,2013)

时变重力数据获取的方法主要有两种：一是通过在固定台站设置重力仪连续观测获得连续重力变化；二是通过对野外固定点的定期复测获得重力变化信息.前者具有观测精度高（μGal级）和时变采样率高（可达秒采样）的优势，但建站成本高、台站数量少；后者观测精度在10μGal级且时间采样间隔长（半年至多年），但设站较为自由、观测密度高，有利于区域性重力变化信息的获取.目前在连续重力观测方面，以gPhone弹簧型和GWR超导型为代表的两种相对重力仪是固定台站常用设备，其中GWR（OSG型和iGrav型）也是当前最高精度的重力观测设备，观测精度优于0.05μGal，采样间隔最高可达1 s（Crossley et al.,2013）；在固定点定期复测方面，常用设备包括FG5型和A10型绝对重力仪，以及LaCoste Romberg（G）型、CG5型和Burris型弹簧型相对重力仪（赵云峰等，2018）.其中，FG5和A10的重力测量精度分别可以达到2μGal和10μGal（Crossley et al.,2013）.

2.1 构建时变重力场模型

我国陆地重力观测系统多以绝对和相对重力仪组网、定期复测的形式获得重力场随时间变化，例如“中国地壳运动监测网络”重力观测系统（许厚泽，2003；祝意青等，2012）.各期重力观测数据经各项改正和重力网平差后，通过不同差分方式（两期差分或以某期为基准差分）获得重力场时变信息（李辉等，2009；祝意青等,2012,2013b），可为区域构造活动分析、地震风险性评估、地震前兆特征提取以及水资源变化监测等研究提供数据支持.基于以上信息建立时变重力场模型时，国内学者目前主要采用空间域方法（申重阳等,2009;Shen et al.,2015;Hao et al.,2021），如最小二乘配置法（祝意青等，2013a，2017；徐伟民等，2021）、Kriging 方法（祝意青等，2015，2016）和等效源方法（张贝等，2021）.

除空间域方法外，谱方法也逐渐被应用到时变重力场建模研究中.玄松柏等（2012）基于小波变换方法获得了2000～2007年中国大陆重力场时变信息的多尺度分解，给出了不同小波尺度下的重力场时变信息及其与构造活动的关联. 陈石等（2018）将Slepian 局部谱分析方法引入到地面时变重力场建模中，利用“中国地壳运动监测网络”2005年和2008年两期重力观测数据，建立了我国大陆区域72阶的重力场模型.韩建成等（2021）基于Slepian方法和我国华北重力测网2011～2013年期间多期重力数据，获得了华北地区120阶（约150 km空间分辨率）的2011～2013年变化重力场模型，并与研究区域内基于Slepian方法和GRACE（Gravity Recovery and Climate Experiment）卫星数据得到的重力变化进行了比较.Han等（2021）将Slepian方法应用到我国川滇地区，获得了该地区2015～2017年120阶时变重力场模型，发现2015～2017年同期差分重力变化受西昌—玉溪一带的近南北向构造和北西向的红河断裂控制.

图2所示即为韩建成等（2021）基于Slepian局部谱分析方法获得的120阶华北地区2011～2013年尺度重力变化，所恢复重力场信号较好地都集中在研究区域（洋红色闭合曲线）内部.

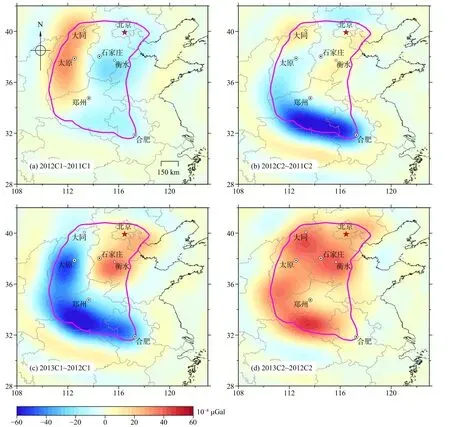
图2 我国华北地区2011～2013年利用Slepian方法确定的120阶1年尺度重力场变化（修改自韩建成等，2021），其中C1和C2分别表示上下半年的不同观测，洋红色线为研究区域边界.单位为μGalFig.2 Spatial pattern of the annual gravity changes up to degree 120 determined by the Slepian method in North China from 2011 to 2013(modified from Han et al.,2021),C1 and C2 denote different campaigns in the first and second half of the year,and the magenta line denotes the boundary of the study area.Units are in μGal

重复重力测点位置空间分布不均匀是目前时变重力场建模面临的主要限制.在点位分布稀疏的地区，不仅重力测网对异常场源的分辨能力受到限制，重力场建模的精度也受到明显影响，韩建成等（2021）报告了在华北地区基于EGM2008模型的模拟实验结果，以研究区域内EGM2008模型120阶FGA（变化范围约58 mGal）模拟重力变化，然后基于Slepian方法解算120阶模型；解算得到的120阶模型的重力变化范围约55 mGal，解算误差为2.50 mGal，在研究区域内观测点位密集的京津地区，解算误差为2.05 mGal；在观测点位较为稀疏的河南、安徽和山东区域，解算误差显著增大至2.98 mGal.综上，在测点分布稀疏地区对重力测网进行加密，将大幅提高重力场建模的精度.

相对重力观测过程中的误差也是影响时变重力场建模精度的重要因素，其中主要包括相对重力仪的非线性漂移和格值系数变化两项误差来源.针对这两项误差源，Chen等（2019）提出了贝叶斯重力网平差模型，该方法可以较好地解决多台相对重力仪器联合平差的权系数优化和非线性漂移估计等问题.王林海等（2020）在此基础上做了改进，将仪器格值的最优化估计问题包含到平差模型中.对我国华南地区2015～2018年实测流动重力观测资料的处理表明，该测网由相对重力仪非线性漂移和格值系数变化导致的不确定性可达20μGal，通过贝叶斯平差模型可以有效抑制这两项误差源的影响（杨锦玲等，2021）.

2.2 探测微弱动力学信号

现代重力观测技术的迅速革新，尤其是超导重力观测技术的成功应用，使得利用地面时变重力数据（主要为台站观测数据）探测地球内部微弱动力学信号成为可能.孙和平等（2017）系统全面地总结了基于现代高精度重力时变观测来探测地球内部动力学信号（地球自由振荡、自由核章动、内核平动振荡等）的研究进展.本节在此基础上，补充一些较新的研究成果与进展.在地球自由振荡方面，王迪晋等（2018）提出了一种具有频率依赖特性的气压改正方法，可精细消除气压变化对超导重力观测的影响，令检测得到的自由振荡各简正模具有更高的信噪比，获得精度更高的基频球型振荡0S2和0S3以及一阶球型振荡1S2分裂谱峰.Sun等（2019）利用低噪声超导重力仪测站的重力记录，讨论分析了BFO（Background Free Oscillations）的激发机制，定性证明了大气干扰是其主要激发源.在自由核章动方面，Cui等（2018）评估了目前超导重力仪观测水平下自由核章动周期变化的可探测性.孙和平等（2018）基于武汉地区高精度重力数据和全球高精度甚长基线干涉（very long baseline interferometry）资料确定了自由核章动本征参数，同时获得了液核顶部的黏滞系数和液核的真实动力学椭率，并基于Monte Carlo方法研究了本征周期的不确定度.

2.3 估计地壳构造变形速率

非潮汐重力变化与地壳物质变形密切相关，其中地表变形的影响较为显著，地表发生隆起或凹陷都会导致地表重力场发生变化.通过分析重力场变化与地表垂向位移变化之间的关系，可研究构造活动区的物质变形和分布规律.Sun等（2009）研究了拉萨、昆明、大理多年连续的GPS和绝对重力时变测量结果，其中，GPS结果表明青藏高原以1.2 mm/a的速率隆升；扣除影响重力变化的垂直位移和剥蚀等因素后，得到绝对重力平均年变化量为−0.78±0.47 mGal/a，表明青藏高原下面的质量在逐渐减少.Sun等（2009）讨论认为青藏高原地壳在长时间挤压下变形，地壳隆升且不断增厚，并以此估算青藏高原底部增厚变形速率为2.3±1.3 cm/a.Sun等（2011）验证了此前在青藏高原的工作，除陆地时变重力和GPS数据外，新增GRACE数据并考虑GIA（Glacial Isostatic Adjustment）效应，更详细地分析研究了青藏高原的构造变形.Sun等（2011）所得陆地重力结果与GRACE结果较为一致，并重新推估地壳增厚速率为1.9±1.4 cm/a.邢乐林等（2011）进行了跟踪性研究，基于拉萨绝对重力资料和GPS数据给出拉萨地壳增厚速率为3.9±0.8 cm/a.邢乐林等（2017）联合绝对重力和GRACE重力多年观测数据，获得了青藏高原5个基准站区域的地壳垂直形变速率.研究结果表明青藏高原平均隆升速率约为1.94±0.17 mm/a，平均增厚速率约为2.35±3.30 mm/a.

陆地时变重力测量还可以用来监测GIA（Lambert et al.,2006;Mazzotti et al.,2011;Sato et al.,2012）.

不管是基于时变重力观测研究深部地壳增厚，还是GIA，都需其他大地测量手段（如GNSS）的辅助，这些辅助观测的不确定度会直接影响整体研究结果的不确定度.

2.4 估计地下水储量变化

给水度（specific yield,Sy）代表地下水位下降后，单位体积含水层所能释出的重力水的体积，是估计地下水储量变化的重要水文地质参数（冯伟等，2017）.通常Sy由抽水试验估算得出，该方法需在研究区新建水井并做跨井抽水实验，成本高昂，不适合对高空间分辨率的Sy进行采样（Chen K-H et al.,2018）.抽水或自然含水层衰退会引起重力变化和地表变形，无需新建地下水井、基于观测已有水井附近的重力变化即可确定Sy的重力法较跨井抽水试验法更经济便捷（Pool and Eychaner,1995;Gehman et al.,2009;Chen K-H et al.,2018,2020）.Chen K-H等（2018）基于2013～2017年中国台湾4处抽水井附近测点的FG5重力仪时变重力测量数据和沉降观测，利用重力法估计了Sy，其中两处Sy估计与常规抽水实验法给出的结果一致.Chen等（2020）收集分析了中国台湾中部浊水河冲积扇和名竹盆地共10个靠近地下水井的重力测点2012～2017年FG5观测数据，基于重力法获得的Sy与跨井抽水试验的Sy值基本一致.Chen等（2020）在不同时间下相同深度范围内的重复试验表明重力法估计Sy值是稳定可复现的.

需要说明的是，根据钻探数据显示，常规抽水实验法和重力法所确定的Sy值代表不同含水层上系数（Chen K-H et al.,2018）.此外，尽管目前重力法能确定与常规抽水方法较为一致的Sy值，而且能经济便捷地提供更高空间分辨率的结果，但重力法并不能完全替代常规方法；常规方法除了给出Sy值外，还能给出其他重要的水文地质参数.

2.5 分析与火山、地震过程的关联

由火山内部岩浆运移引起的陆地重力变化十分显著，通常可以达到百μGal量级. Battaglia（1999）分析了美国加州东部Long Valley火山口附近1982～1998年期间的重复重力观测数据，认为经过各项改正后约60μGal的重力增加与火山口下方高密度的岩浆侵入有关.Branca等（2003）对比了意大利西西里岛东岸的Etna火山2002年10月喷发前后的重力变化信号，结果显示在喷发前1小时内重力减小了约400 μGal，喷发后重力迅速恢复到正常变化水平.Mouyen等（2016）分析了自2005年以来中国台湾大屯火山群连续的超导重力观测时间序列，扣除地下水导致的重力变化后，发现2007年由流体压力引发的地震导致了约35μGal的重力变化.

地面时变重力观测目前是研究地震前兆信息的重要技术方法之一（Zhan et al.,2011;陈石等,2015;毛经伦和祝意青,2018;祝意青等,2018;胡敏章等,2019;申重阳等,2020）.陈运泰等（1980）认为在1975年海城MS7.3和1976年唐山MS7.8地震前都存在地面重力时变现象.祝意青等（2009）以及Zhu等（2010）通过处理分析2008年MS8.0汶川地震前绝对重力和相对重力观测数据，认为区域性的重力场变化可能与地震孕育、发生过程有关.Zhan等（2011）分析了1998年、2000年、2002年和2005年“中国地壳运动监测网络”的陆地重力测量数据，发现2001年11月至2008年8月期间中国大陆和台湾区域共9次大地震发生之前，在较大区域范围内出现了明显的重力变化.基于对一台超导重力仪和11个宽频带地震仪数据的分析讨论，Shen等（2011）发现2008年汶川地震前存在异常信号.Chen等（2016）分析了青藏高原4个绝对重力点（拉萨、那曲、日喀则和仲巴）重复观测结果，发现2015年4月25日尼泊尔MW7.8地震前存在重力增加现象，并估算了该地震前的重力场源范围与震质中位置（图3）.胡敏章等（2019）通过对实际震例的分析，总结了地震孕育与重力变化之间的时空关系，建立了基于重力变化来分析预报地震的经验性依据.

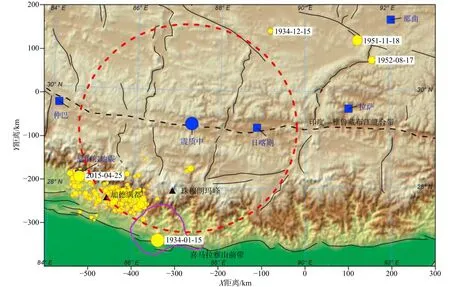
图3 2015年4月25日尼泊尔地震前的重力场源范围（红色虚线以内）和震质中位置（蓝色圆）（修改自Chen等，2016）.其中蓝色方块为绝对重力点，分别为拉萨、那曲、日喀则和仲巴.黄色圆代表震中位置，没有时间标记的黄色圆为尼泊尔地震大于4级的余震震中位置Fig.3 The location of the modeled source region(within the red dashed circle)and its epicentroid(the blue circle)of the April 25,2015 Nepal earthquake(modified from Chen et al.,2016).The blue squares denote the absolute gravity stations,the yellow circles denote the epicenters,and the yellow circles without time stamp denote the epicenters of the aftershocks of the Nepal earthquake (with magnitude> 4)

地震的孕育机制和发生过程均异常复杂，加之地球“不可入性”以及大地震“非频发性”的影响，地震预测是全世界极具挑战性的科学难题之一（陈运泰，2009）.尽管目前基于高精度地面时变重力观测的地震前兆分析以及预报取得了一些有意义的进展，但总体上仍处于经验性的初步研究阶段（胡敏章等，2019）.

3 陆地重力观测的新趋势

3.1 新的观测仪器

陆地重力观测离不开高精度重力仪的支持，重力仪的革新也主导了陆地重力观测数据分析理论和技术的发展（Crossley et al.,2013）.原子干涉重力测量技术经过多年的发展，目前国际上已经成功实现商业化，其产品精度水平与FG5绝对重力仪相当，兼具测量灵敏度高和长期稳定运行的优势（Ménoret et al.,2018），是下一代绝对重力测量仪器的首选.

当前我国高精度重力仪器设备主要依赖进口，不仅容易遭受国外垄断技术“卡脖子”，而且存在国家安全相关数据外泄的隐患.近年来，国内多家单位在重力仪器研究领域取得重大突破，相继研发出不同类型的重力仪，其中包括实用化和小型化的原子干涉重力仪（孙和平等，2021）.尽管我们在发展具备完全自主知识产权的国产重力仪器上迈出了从无到有的关键一步，但国产设备还未实现成熟的商业化，未来仍需要较长时间才能完成大规模列装.

3.2 新的观测方法

在重力观测仪器迅速发展的同时，陆地高精度、可复测的重力观测系统也在不断发展，如组合多种观测设备的陆地重力梯度测量方法（Kennedy et al.,2014）.这种方法也被称为变基线重力梯度方法（variable baseline gravity gradient method），即高精度的地面梯度测量.图4为不同重力测量方法对地下场源的敏感性分析结果，图4a为使用一台重力仪进行测量，图4b为水平距离不同（分别为10 m和80 m）的两台重力仪测量（也可认为是水平梯度测量）.通过对比可以发现，不同距离的水平梯度测量对于场源敏感程度存在显著差别.因此，通过设计多方式组合的重力观测系统，将有利于识别特定时空尺度的场源重力信号（Kennedy et al.,2014;陈石等,2018）.

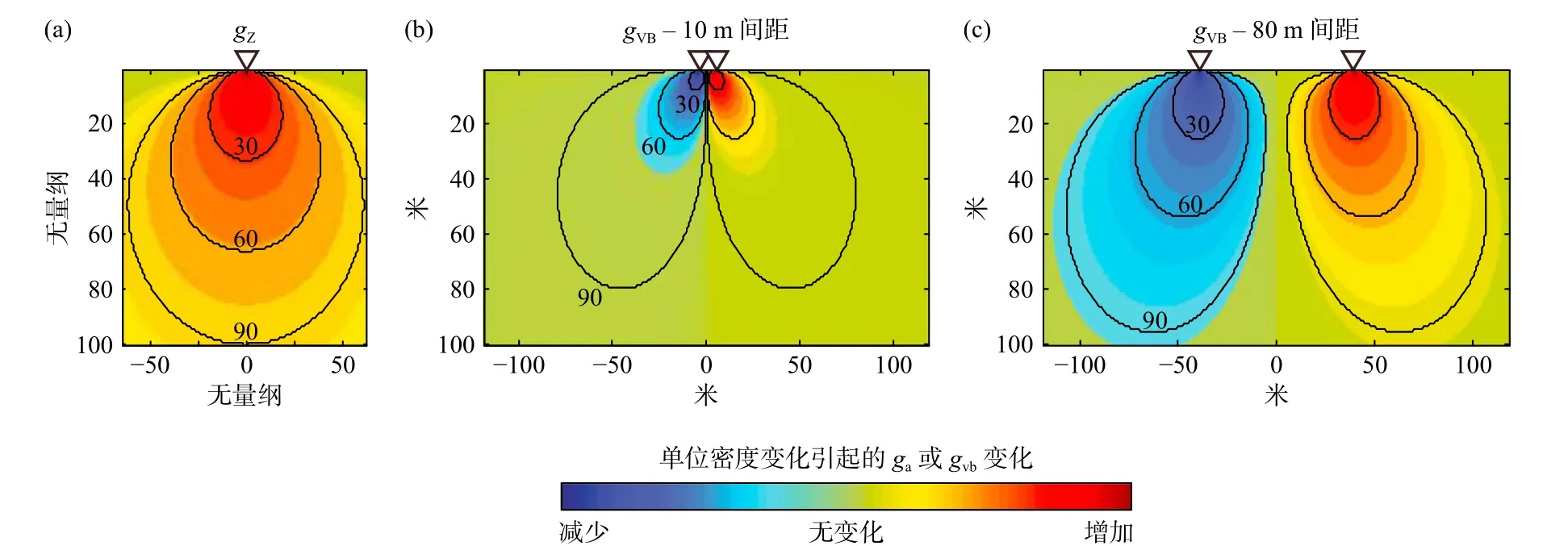
图4 陆地重力测量的敏感度分布.（a）使用一台重力仪；（b）使用水平间隔10 m和80 m的两台重力仪（修改自Kennedy et al.,2014）.三角代表重力仪，30、60和90为敏感度等值线Fig.4 Sensitivity distributions for terrestrial gravity measurement using(a)a single gravimeter,(b)two meters separated by 10 m and 80 m horizontally (modified from Kennedy et al.,2014).The triangles are gravimeters and the lines labeled 30,60 and 90 denote the cumulative sensitivity contours

3.3 新的数据处理技术

在本文第2.1节，我们已经讨论过相对重力观测过程中的主要误差来源，即相对重力仪的非线性漂移和格值系数变化.传统的线性漂移处理和格值标定方法，并不能有效地消除这两项误差.Chen等（2019）提出、王林海等（2020）改进的贝叶斯重力网平差模型，则可较好地解决非线性漂移估计和格值系数优化问题.贝叶斯重力网平差模型为绝对和相对重力仪组网观测数据的处理提供了新的选择，该模型的可靠性和有效性也已被多个应用实例证明（Chen et al.,2019;王林海等,2020;杨锦玲等,2021）.

贝叶斯重力网平差模型已作为功能模块添加到geoist软件包中（Chen et al., 2020），最新版geoist 软件可由网址https://github.com/igp-gravity/geoist 或 https://cea2020.gitee.io/geoistdoc获取.

3.4 现有观测系统的全面升级

经过60多年的持续发展，中国大陆时变重力观测系统已经实现了多次重大升级（祝意青等，2018；申重阳等，2020），目前仍在进一步优化中.中国地震局2020年发布的《中国地球物理站网（重力）规划》（中国地震局，2020）指出，到2030年将建成我国大陆地区相对均匀的基准网和基本网、活动块体边界带和重点地区适度加密的区域网观测系统，对我国大陆及周边岩石圈构造运动实现整体监测，提供μGal级时变重力场变化图像.本次升级将全面提升我国陆地重力观测网络的标准化、信息化和现代化水平，其观测数据不仅满足地震行业需求，还可为地球科学和经济建设等领域提供数据保障.

4 结语

随着重力观测技术的提高和地面观测网络的日益完善，以及观测资料的长期积累，陆地高精度的重力模型产品和时变重力数据在大地测量学和地球物理学领域得到了广泛应用，近十几年来取得了众多的科研成果，深化了对地球基本属性、内部结构和动力学现象的认识和理解.

应用陆地高精度静态重力场的研究方面：

（1）重力场和大地水准面模型方面：近年来的精化过程仍依赖数量更多、覆盖更广的高精度数据，尤其是填补空白区的高精度数据.

（2）地壳物性结构模型方面：联合反演仍是建立可靠地壳结构模型的有效途径，近年来的新发展是利用自由空气重力异常数据估计近地表的密度变化，然后根据密度变化计算更加合理的布格重力异常.鉴于我国很多区域存在μGal级的自由空气重力异常产品，这一新发展未来可能会大幅提升反演得到的地壳结构模型的可靠性.

（3）Moho界面形态方面：附加约束信息仍然是近年来优化反演结果的主要途径.

（4）岩石圈有效弹性厚度（Te）方面：尽管近年来空间域的方法有所发展，谱方法仍是常用方法，但其不利于研究Te的横向变化特征.目前存在的另一个主要问题是不同研究给出的中国大陆地区Te不尽相同，而且空间分辨率较低.

应用陆地高精度时变重力场的研究方面：

（1）时变重力场模型方面：近年来的新进展是基于谱方法确定重力场变化，谱方法可从观测数据中提取所需的信号频段，这一点常用的空间域方法难以实现. 值得指出的是，第2.1节中介绍的Slepian谱分析方法，其展开与同阶次经典球谐展开具有相同的意义，这一点利于联合陆地重力数据和现有球谐重力场模型构建融合模型.

（2）微弱地球动力学信号方面：近年来的发展仍依赖长期的持续观测，以进一步提高数据的信噪比.

（3）地壳构造变形速率方面：量化确定各种辅助数据（如GNSS数据）的不确定度是近年来应用研究的重要环节.

（4）地下水储量变化方面：基于时变绝对重力观测确定给水度Sy是近年来的新进展，该方法较传统方法更加便捷高效，而且可提供更高空间分辨率的结果，局限之处是所确定的水文地质参数较为单一.

（5）火山、地震过程的可能关联方面：近年来的新进展是地震孕育与重力变化之间的经验性时空关系，尽管已取得一些有意义的结果，目前这一关系仍然处在初步研究阶段.

通过梳理总结近十几年来相关领域的陆地重力数据应用成果，本文可为中国大陆重力观测系统的建设、发展和规划提供一定参考.陆地重力测量在观测仪器方面，以高精度激光干涉和冷原子技术为代表的绝对重力观测仪器不断成熟，为研究时变微重力信号提供了可靠的基准.在测量方法和数据处理方面，新的突破也开始出现.在观测网络方面，中国大陆重力观测网络作为目前全球最大规模测网，未来应更注重高质量数据产品和科研成果的产出.陆地重力观测在未来十年将迎来快速发展时期，更多高质量重力观测数据产品会不断丰富，将为以高精度陆地观测数据为支撑的科学研究提供强大助力，势必进一步推动相关领域的发展，为我们揭示更多地球内部的未知信息.

附中文参考文献

陈石，王谦身，祝意青，等.2011.青藏高原东缘重力导纳模型均衡异常时空特征[J].地球物理学报，54（1）：22-34.

陈石，徐伟民，石磊，等.2013.龙门山断裂带及其周边地区重力场和岩石层力学特性研究[J].地震学报，35（5）：692-703.

陈石，王青华，王谦身，等.2014.云南鲁甸MS6.5地震震源区和周边三维密度结构及重力场变化[J].地球物理学报，57（9）：3080-3090.

陈石，徐伟民，蒋长胜.2015a.中国大陆西部重力场变化与强震危险性关系[J].地震学报，37（4）：562-574.

陈石，郑秋月，徐伟民.2015b.南北地震带南段地壳厚度重震联合最优化反演[J].地球物理学报，58（11）：3941-3951.

陈石，龚立卓，徐伟民，等.2018.深部场源变化微重力观测系统设计与模型研究[J].大地测量与地球动力学，38（1）：1-4.

陈晓东，李航，邓明莉，等.2020.用重力测量技术观测城市地表下沉的实验研究[J].地球物理学报，63（8）：2882-2892.

陈运泰，顾浩鼎，卢造勋.1980.1975年海城地震与1976年唐山地震前后的重力变化[J].地震学报，2（1）：21-31.

陈运泰.2009.地震预测:回顾与展望[J].中国科学:地球科学，39（12）：1633-1658.

党亚民，郭春喜，蒋涛，等.2021.2020珠峰测量与高程确定[J].测绘学报，50（4）：556-561.

冯锐.1985.中国地壳厚度及上地幔密度分布（三维重力反演结果）[J].地震学报，7（2）：143-157.

冯伟，王长青，穆大鹏，等.2017.基于GRACE的空间约束方法监测华北平原地下水储量变化[J].地球物理学报，60（5）：1630-1642.

付广裕，金红林，王灼华，等.2018.汶川MW7.9地震周边地区布格重力异常与岩石圈垂向构造应力场[J].地震，38（2）：28-36.

付广裕，王振宇.2020.新疆精河6.6级地震周边地区密度构造、均衡异常以及岩石圈挠曲机理[J].地球物理学报，63（6）：2221-2229.

郭俊义.2001.地球物理学基础[M].北京：测绘出版社

郭良辉，孟小红，石磊，等.2012.优化滤波方法及其在中国大陆布格重力异常数据处理中的应用[J].地球物理学报，55（12）：4078-4088.

郭震，陈永顺，殷伟伟.2015.背景噪声面波与布格重力异常联合反演:山西断陷带三维地壳结构[J].地球物理学报，58（3）：821-831.

韩建成.2012.基于地球重力场模型和地表浅层重力位确定大地水准面[D].武汉：武汉大学.

韩建成，陈石，卢红艳，等.2021.基于Slepian方法和陆地重力观测确定时变重力场模型:以2011–2013年华北地区数据为例[J].地球物理学报，64（5）：1542-1557.

胡明城.2003.现代大地测量学的理论及其应用[M].北京:测绘出版社.

胡敏章，李建成，李辉，等.2015.西北太平洋岩石圈有效弹性厚度及其构造意义[J].地球物理学报，58（2）：542-555.

胡敏章，郝洪涛，李辉，等.2019.地震分析预报的重力变化异常指标分析[J].中国地震，35（3）：417-430.

胡敏章，金涛勇，郝洪涛，等.2020.青藏高原东南缘岩石圈有效弹性厚度及其构造意义[J].地球物理学报，63（3）：969-987.

黄建平，傅容珊，许萍，等.2006.利用重力和地形观测反演中国及邻区地壳厚度[J].地震学报，28（3）：250-258.

贾民育.2000.微重力测量技术的应用[J].地震研究，23（4）：452-456.

姜效典，李德勇，宫伟，等.2014.青藏高原东西向差异形变与隆升机制[J].地球物理学报，57（12）：4016-4028.

雷晓东，戚帮申，关伟，等.2021.北京平原区断裂构造重力异常识别研究[J].地球物理学报，64（4）：1253-1265.

李辉，申重阳，孙少安，等.2009.中国大陆近期重力场动态变化图像[J].大地测量与地球动力学，29（3）：1-10.

李红蕾，方剑，王新胜，等.2017.重力及重力梯度联合反演青藏高原及邻区岩石圈三维密度结构[J].地球物理学报，60（6）：2469-2479.

李红蕾，陈石，庄建仓，等.2021.贝叶斯同化重力反演方法构建龙门山地壳密度模型[J].地球物理学报，64（4）：1236-1252.

李海龙，吴招才，纪飞，等.2020.南海北部地壳密度结构:基于约束三维重力反演[J].地球物理学报，63（5）：1894-1912.

李建成,陈俊勇,宁津生,等.2003.地球重力场逼近理论与中国2000似大地水准面的确定[M].武汉：武汉大学出版社.

李建成.2012.最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J].测绘学报，41（5）：651-660,669.

李永东，郑勇，熊熊，等.2013.青藏高原东北部岩石圈有效弹性厚度及其各向异性[J].地球物理学报，56（4）：1132-1145.

刘经南，罗志才，李建成.2000.从第22届IUGG大会看现代大地测量的进展[J].武汉测绘科技大学学报，25（1）：12-17,48.

楼海.2001.重力方法在地壳结构研究中的应用[D].北京：中国地震局地球物理研究所.

鲁宝亮，王万银，赵志刚，等.2018.南海深部构造特征及其地质意义:来自重磁位场反演的认识[J].地球物理学报，61（10）：4231-4241.

马宗晋，高祥林，宋正范.2006.中国布格重力异常水平梯度图的判读和构造解释[J].地球物理学报，49（1）：106-144.

毛经伦，祝意青.2018.陆地重力观测数据在地震预测中的应用研究与进展[J].地球科学进展，33（3）：236-247.

牛源源，郭良辉，石磊，等.2019.近地表密度估计的重力贝叶斯分析方法及在云南地区的应用[J].地球物理学报，62（6）：2101-2114.

秦朋波，黄大年.2016.重力和重力梯度数据联合聚焦反演方法[J].地球物理学报，59（6）：2203-2224.

区域重力调查规范编写组.2006.区域重力调查规范(DZ/T 0082—2006)[S].中华人民共和国国土资源部.

佘雅文，付广裕，高原，等.2018.华北地区中东部岩石圈挠曲与均衡特性以及地震活动性分析[J].地球物理学报，61（11）：4448-4458.

申重阳，李辉，孙少安，等.2009.重力场动态变化与汶川MS8.0地震孕育过程[J].地球物理学报，52（10）：2547-2557.

申重阳，杨光亮，谈洪波，等.2015.维西—贵阳剖面重力异常与地壳密度结构特征[J].地球物理学报，58（11）：3952-3964.

申重阳，祝意青，胡敏章，等.2020.中国大陆重力场时变监测与强震预测[J].中国地震，36（4）：729-743.

石磊，楼海，王谦身，等.2015.攀西地区重力场特征及地壳密度结构[J].地球物理学报，58（7）：2402-2412.

侍文，陈石，韩建成，等.2021.中国大陆岩石圈有效弹性厚度与强震构造区力学特征研究[J].地震，41（1）：1-12.

孙和平，徐建桥，崔小明.2017.重力场的地球动力学与内部结构应用研究进展[J].测绘学报，46（10）：1290-1299.

孙和平，刘清超，崔小明，等.2018.利用重力和VLBI技术检测地球液态核的动力学效应[J].武汉大学学报·信息科学版，43（12）：2058-2063.

孙和平，孙文科，申文斌，等.2021.地球重力场及其地学应用研究进展——2020中国地球科学联合学术年会专题综述[J].地球科学进展，36（5）：445-460.

索奎，张贵宾，江国明，等.2015.重震反演中国东北地壳上地幔三维密度结构[J].地球物理学报，58（7）：2436-2444.

王迪晋，刘子维，韦进，等.2018.基于EEMD分解的气压改正方法研究[J].地球物理学报，61（2）：504-520.

王林海，陈石，庄建仓，等.2020.精密重力测量中相对重力仪格值系数的贝叶斯估计方法[J].测绘学报，49（12）：1543-1553.

王谦身，滕吉文，张永谦，等.2009.四川中西部地区地壳结构与重力均衡[J].地球物理学报，52（2）：579-583.

王鑫，姜文亮，张景发，等.2020.青藏高原东北缘重力场深部结构及其动力学特征[J].地球物理学报，63（3）：988-1001.

王新胜，方剑，许厚泽，等.2012. 华北克拉通岩石圈三维密度结构[J].地球物理学报，55（4）：1154-1160.

王新胜，方剑，许厚泽.2013. 青藏高原东北缘岩石圈三维密度结构[J].地球物理学报，56（11）：3770-3778.

吴怿昊，罗志才，周波阳.2016.基于泊松小波径向基函数融合多源数据的局部重力场建模[J].地球物理学报，59（3）：852-864.

吴招才，高金耀，丁巍伟，等.2017.南海海盆三维重力约束反演莫霍面深度及其特征[J].地球物理学报，60（7）：2599-2613.

邢乐林，孙文科，李辉，等.2011.用拉萨点大地测量资料检测青藏高原地壳的增厚[J].测绘学报，40（1）：41-45.

邢乐林，王林海，胡敏章，等.2017.时变重力测量确定青藏高原地壳隆升与增厚速率[J].武汉大学学报(信息科学版)，42（5）：569-574.

许才军，尹智.2014.利用大地测量资料反演构造应力应变场研究进展[J].武汉大学学报(信息科学版)，39（10）：1135-1146,1178.

许厚泽.2003.重力观测在中国地壳运动观测网络中的作用[J].大地测量与地球动力学，23（3）：1-3.

许厚泽，陆洋，钟敏，等.2012.卫星重力测量及其在地球物理环境变化监测中的应用[J].中国科学:地球科学，42（6）：843-853.

徐伟民，陈石，阮明明，等.2021.川滇地区陆地流动重力测网场源分辨能力评估[J].地震，41（1）：191-204.

玄松柏，邢乐林，谈洪波，等.2012.中国大陆2000-2007年重力场变化多尺度分解[J].大地测量与地球动力学，32（3）：7-16.

杨光亮，申重阳，黎哲君，等.2020.巴颜喀拉地块东部及邻区重力均衡与岩石圈有效弹性厚度[J].地球物理学报，63（3）：956-968.

杨锦玲，陈石，王林海，等.2021.华南陆地时变重力观测数据质量评估[J].测绘学报，50（3）：333-342.

杨亭，傅容珊，黄金水.2013.利用Moho地形导纳法 (MDDF)反演中国大陆岩石圈有效弹性厚度[J].地球物理学报，56（6）：1877-1886.

姚宜斌，杨元喜，孙和平，等.2020.大地测量学科发展现状与趋势[J].测绘学报，49（10）：1243-1251.

张贝，陈石，李红蕾，等.2021.时变重力场球面模型反演算法和模拟实验[J].地震，41（1）：13-24.

章传银，郭春喜，陈俊勇，等.2009.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报，38（4）：282-289.

张杰，杨光亮，谈洪波，等.2020.基于接收函数约束的川滇地区莫霍面深度反演研究[J].地球物理学报，63（7）：2579-2591.

张晰，王芃，邓阳凡，等.2016.利用重力异常构建壳幔密度结构方法及应用[J].地球物理学进展，31（1）：143-151.

张永谦，王谦身，滕吉文.2010.川西藏东地区的地壳均衡异常及其与地震分布的关系[J].地球物理学报，53（11）：2631-2638.

赵云峰，祝意青，梁伟锋，等.2018.Burris型重力仪性能分析[J].地震地磁观测与研究，39（2）：178-185.

郑勇，李永东，熊熊.2012.华北克拉通岩石圈有效弹性厚度及其各向异性[J].地球物理学报，55（11）：3576-3590.

中国地震局.2020.中国地球物理站网（重力）规划（2020-2030）[R].北京.https://www.cea.gov.cn/cea/xwzx/zyzt/5576318/5576317/5576635/index.html.

祝意青，徐云马，吕弋培，等.2009.龙门山断裂带重力变化与汶川8.0级地震关系研究[J].地球物理学报，52（10）：2538-2546.

祝意青，梁伟锋，湛飞并，等.2012.中国大陆重力场动态变化研究[J].地球物理学报，55（3）：804-813.

祝意青，闻学泽，孙和平，等.2013a.2013年四川芦山MS7.0地震前的重力变化[J].地球物理学报，56（6）：1887-1894.

祝意青，闻学泽，张晶，等.2013b.华北中部重力场的动态变化及其强震危险含义[J].地球物理学报，56（2）：531-541.

祝意青，刘芳，李铁明，等.2015.川滇地区重力场动态变化及其强震危险含义[J].地球物理学报，58（11）：4187-4196.

祝意青，李铁明，郝明，等.2016.2016年青海门源MS6.4地震前重力变化[J].地球物理学报，59（10）：3744-3752.

祝意青，梁伟锋，赵云峰，等.2017.2017年四川九寨沟MS7.0地震前区域重力场变化[J].地球物理学报，60（10）：4124-4131.

祝意青，申重阳，张国庆，等.2018.我国流动重力监测预报发展之再思考[J].大地测量与地球动力学，38（5）：441-446.