计及需求响应的峰谷分时电价研究

张效言，李先允

(南京工程学院 电力工程学院， 江苏 南京 211167)

0 引 言

智能电网和新能源的发展使需求响应(demand response，DR)越来越多地受到人们的重视[1]。作为需求响应的重要措施，峰谷分时电价政策在国内外已经推广并逐渐普及[2]。通过价格杠杆激励用户改变用电方式，实现对需求侧资源的调度，达到转移负荷的目的，提高了系统的可靠性和经济性[3]。国内外学者对需求响应进行了相关研究。文献[4]提出了可以代表用户行为的综合需求响应模型，并以此建立实时电价优化模型进行日前定价。文献[5]基于实时电价，提出了一种住宅能源消耗调度模型，根据用户的需求在最小化支付和最小化家用电器运行的等待时间之间实现权衡。相较于国外大多使用实时电价(real-time electricity price, RTP)进行调控，我国主要采用相对折中的分时电价(time-of-use electricity price, TOU)进行调控。文献[6]考虑边际电价，建立了基于负荷率分档模型并划分了峰谷时段。文献[7]首先分析不同用户的用电特性，然后基于博弈模型，提出了一种同时考虑电网和用户利益的分时电价制定方法。

本文基于需求响应理论，首先建立了分时电价模型，然后提出了一种改进粒子群算法对建立模型进行求解，该算法在粒子群全局最优粒子周围随机取点，用支持向量机回归(support vector machine regression, SVR)预测最优随机点，将其替换原种群中一个非最优粒子，随着迭代过程的增加，粒子群粒子不断更新，从而实现迭代寻优。算例分析表明建立的分时电价模型促进了负荷曲线削峰填谷，同时减少了用户的成本，提出的改进粒子群算法能更快、更精确地对模型进行求解，具有很好的应用价值。

1 基于需求响应的分时电价优化模型

以负荷曲线标准差最小为优化目标，考虑用户获益，多时段用户需求响应等为约束条件，建立分时电价优化模型。

1.1 目标函数

目标函数如式(1)、式(2)所示。

(1)

(2)

式中：E(t)为t时刻的用电量；Eav为负荷曲线平均值；T为典型小时数。

1.2 约束条件

1) 用电量约束

实施分时电价前后应保证用户负荷总量不变，如式(3)所示。

E0=ETOU

(3)

式中:E0、ETOU分别为原用电量和采用分时电价后的用电量。

2) 成本约束

考虑发电成本及用户的承受能力，必须对电价进行约束，计算式如式(4)所示。

eiTOU min≤eiTOU≤eiTOUmax

(4)

式中:eiTOU为i时段分时电价；eiTOUmin和eiTOUmax分别为分时电价的最大及最小值，由该时段的边际电价成本及消费水平决定。

3) 用户获益

在分时电价下，用户将一部分高峰负荷转移到低谷以减小电费支出，因此有:

CTOU≤C0

(5)

式中:C0、CTOU分别为实施分时电价前后用户的总电费。其中：

(6)

(7)

式中:e0为原电价；Ei0、EiTOU为采用分时电价前后i时段的用电量。

4) 多时段用户需求响应约束

电能是一种商品，其值会随着价格上下波动，需求价格弹性系数表示用电量对价格的灵敏度，如式(8)所示。

(8)

式中:E、e为电量和电价；ΔE、Δe为电量和电价的相对增量。

考虑用户在受价格刺激时，负荷可以转移到其他时段的多时段需求响应，如式(9)所示[8]。

(9)

式中:εii、εij为自弹性、互弹性系数；eiTOU、ejTOU为采用分时电价之后i、j时段的电价。

2 基于支持向量机回归的改进粒子群算法

建立的分时电价模型是一个非线性模型，常用粒子群等算法求解。Eberhart和Kennedy受鸟群觅食行为的启发于1995年提出粒子群算法(particle swarm optimization, PSO)[9]。核心公式如下：

(10)

(11)

式中:ω为惯性权重；c1、c2为学习因子；r1、r2为[0，1]间的随机数；vid、xid为粒子i在d维的速度、位置；Pid、Gid为在粒子i在d维的个体极值、群体极值；k为迭代次数。PSO易操作、收敛快，但也有易于陷入局部极值等缺点。

采用SVR对粒子群算法进行改进。核心思想为在粒子群全局最优粒子位置周围任取随机点，用SVR预测适应度最优的随机点，将其替换原种群中的一个非最优粒子，然后继续迭代，随着输入回归信息的不断增加，预测越来越精确。步骤如下：

步骤1：初始化粒子群，SVR参数。

步骤2：计算粒子适应度值，得到个体极值Pid和群体极值Gid。记录每个粒子位置和对应的适应度值，并将其分别作为SVR的训练集和训练标签。随后通过PSO计算出支持向量机惩罚系数c和gamma值[9]。

步骤3：计Gid对应的最优位置为Xbest，并在其附近任取随机位置Xran=Xbest+Xbest×Zn，Zn为n个[-1，1]间的随机数。

步骤4：将所取位置Xran作为验证集输入SVR中，得到回归适应度值，比较得出最优回归适应度值及对应位置，并作为新粒子。

步骤5：将新粒子替代原种群中一个非最优适应度粒子。

步骤6：更新粒子的位置和速度。

步骤7：循环执行步骤2～6，直至最大循环次数。输出最后一代中适应度值最优的个体。

3 算例分析

3.1 参数设置

将浙江省某工业园区电网典型日作为分析对象，其负荷曲线如图1所示。原电价e0为0.425 元/kWh, 用户的弹性系数如表1所示[10]。采用模糊C均值聚类对峰谷时段进行划分，得到峰时段为08∶00—11∶00，17∶00—21∶00；平时段为12∶00—16∶00，21∶00—23∶00；谷时段为23∶00—08∶00。

图1 工业园典型日负荷曲线

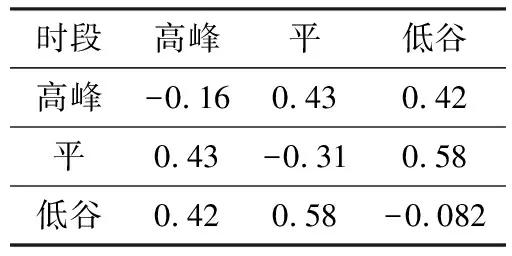
表1 需求弹性系数

由图1可以看出，园区存在高峰和次高峰，且因中午工人午休时出现低谷，峰谷差较大。考虑采用分时电价来引导用户，实现削峰填谷。

3.2 结果分析与比较

采用改进PSO对分时电价定价模型进行求解。粒子群种群为50，c1=c2=1.496 2，ω从0.8到0.4递减，迭代200次，选择应用回归问题的e-SVR，e-SVR中损失函数p=0.1。为了有更好的性能，针对非线性问题选择RBF核函数。

分别采用PSO算法及改进PSO算法对分时电价模型进行求解，设置三种场景进行对比分析，场景1电价为原电价；场景2电价为PSO求解的分时电价；场景3为改进PSO求解的分时电价。改进PSO求解得到峰、平、谷电价分别为0.602 元/kWh，0.366 元/kWh，0.168 元/kWh；采用PSO算法进行求解，得到的峰、平、谷电价分别为0.595 元/kWh，0.382 元/kWh，0.151 元/kWh。三种场景对比如图2所示。

图2 三种场景负荷曲线对比图

由图2可以看出，采用了分时电价之后，负荷曲线实现了一定程度的削峰填谷。三种场景相关参数对比如表2所示。

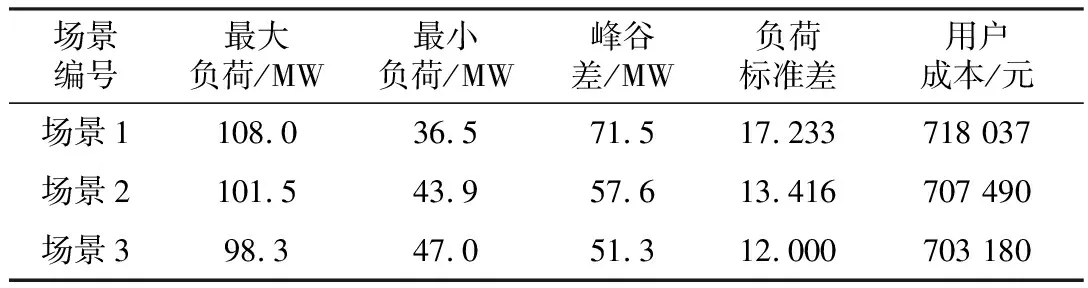
表2 场景对比

通过场景1和场景2对比可以看出，采用分时电价后，负荷曲线的峰谷差从71.5 MW下降到57.6 MW，负荷标准差从17.233下降到13.416，实现了削峰填谷的目的，同时用户支出电费也下降了10 547元，减少了用户的购电成本。通过场景2和场景3对比可以看出，采用改进粒子群算法计算得到的分时电价，更好地实现了削峰填谷目标，得到了更小的峰谷差和标准差，同时用户成本也进一步下降，因此提出的改进PSO算法相比于PSO算法有更好的性能。

4 结束语

本文基于需求价格理论，以削峰填谷为目标，考虑用户获益和电价成本等约束条件，建立了峰谷分时电价优化模型。同时提出了一种基于SVR的改进粒子群算法，可以更快速、精确地制定出合理的分时电价。通过算例分析证明，分时电价可以实现削峰填谷，同时可以减少用户的购电成本，使得电网的可靠性和经济性进一步提高。