一种“源-网-荷-储”协同优化调度模型

王季， 陈瑞

(1.甘肃省机械科学研究院有限责任公司，甘肃 兰州 730030； 2.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050；3.甘肃省工业过程先进控制重点实验室，甘肃 兰州 730050)

0 引 言

智能电网的出现使“源-网-荷-储”协调互动变成了可能，由原来单一简单的传统潮流变为复杂的双向潮流，负荷的主动参与增加了电网调度灵活性[1]。为提高可再生能源的消纳能力，构建清洁能源供应体系，主动配电网环境下“源-网-荷-储”协同优化调度模式应用而生[2]。在配电网规划中，很难通过考虑单个实体或几个实体的利益来最大化每个资源的价值。目前，关于分布式发电、储能和需求响应的优化规划研究很多[3]，但缺乏对“源-网-荷-储”协调规划的综合考虑。

本文提出了一种基于“源-网-荷-储”协同的配电网双层规划模型，并采用了实时优化的协调优化策略，结合遗传随机权重粒子群算法(genetic random weighted particle swarm optimization algorithm，GA-RWPSO)求解规划模型。最后，利用IEEE 33节点系统对模型进行仿真分析，验证了模型的有效性和经济性。

1 “源-网-荷-储”协同的双层优化模型

在“源-网-荷-储”协同优化问题中，既要考虑综合成本和稳定性，又要考虑可靠性[4]。考虑到分布式电源的随机性与波动性对负荷的影响，再加上分布式电源的接入位置与储能的容量大小都会对负荷优化特性曲线产生影响，从而影响调度成本。因此建立了“源-网-荷-储”协同优化调度的双层模型，尽可能达到优化负荷特性曲线的同时，使得系统整体的经济效益和可靠性最优。“源-网-荷-储”协同的双层优化模型，如图1所示。

2 双层优化模型

2.1 上层优化模型

上层计划以最低年度综合成本为目标，包括年度投资成本、年度维护成本和年度网络损耗成本。

图1 “源-网-荷-储”协同的双层优化模型

综合目标函数式如式(1)所示。

minf=Cinv+Cm+Closs

(1)

式中:Cinv为年度投资成本;Cm为年度维护成本;Closs为年度网络损耗成本。计算如式(2)～式(6)所示。

(2)

(3)

(4)

(5)

(6)

2.2 下层优化模型

下层优化模型以负荷变化量最优为目标函数，评价指标为配电网侧综合负荷的波动幅度和波动率，体现了配电网的供电可靠性。

(7)

(8)

minf=η1T+η2T

(9)

2.3 约束条件

“源-网-荷-储”协同优化模型还需满足一定的约束条件。

1) 分布式电源有功出力约束

PDG.min≤PDG(t)≤PDG.max

(10)

式中:PDG.min、PDG.max为分布式电源输出有功功率的最小值和最大值；PDG(t)为配电网中分布式电源实际输出的有功功率。

PDG(t)=(1+μfore)PDG.fore(t)

(11)

0≤μfore≤μfore.max

(12)

式中:μfore为光伏和风电出力的预测误差系数，越接近0说明预测精度越高；PDG.fore(t)为分布式电源有功出力的日前预测值;μfore.max为预测误差系数最大值。

2) 节点电压约束

Ui.min≤Ui≤Ui.max

(13)

式中：Ui.max、Ui.min为节点i允许电压的上下限；Ui为配电网中第i个节点的电压幅值。

3) 支路电流约束

0≤Il≤Il.max

(14)

式中：Il为支路l流过的电流幅值；Il.max为支路l满足条件的最大幅值。

4) 储能响应约束

保证储能工作在正常状态，满足荷电状态SOC约束和充放电功率约束。

(15)

5) 可靠性约束

R≥Rmin

(16)

式中:R为当前系统的可靠性值；Rmin为系统可靠性要求的最低值。

3 模型求解方法

采用GA-RWPSO对“源-网-荷-储”协同优化调度双层模型求解。上层目标为最低年度综合成本，包括年投资成本、年度维护成本和年度网络损耗成本，变量为储能出力和负荷出力；下层目标为负荷变化量最优，变量为日负荷功率。

具体步骤如下：

(1) 输入分布式电源出力和负荷有功功率预测值。

(2) 上层粒子群初始化，储能出力与负荷出力作为粒子。

(3) 下层粒子群初始化，配电网日负荷功率作为粒子。

(4) 利用潮流计算得到粒子适应度值，初始化局部最优值pbest和全局最优值gbest。

(5) 更新迭代惯性权重、粒子的速度和位置。

(6) 对更新后的粒子按照速度和位置约束进行相应处理。

(7) 用改进的选择交叉变异机制对更新后的粒子进行操作。

(8) 进行潮流计算，更新pbest和gbest。

(9) 比较计算下层粒子的适应度，目标为负荷变化量最小。

(10) 如果达到迭代次数则比较计算上层粒子的适应度，如果没有达到迭代次数，则返回第二步。

(11) 判断储能系统和柔性负荷可调用剩余容量，并更新下一时刻优化中相应粒子的取值范围。

(12) 如果达到迭代次数，则输出该时刻储能系统和柔性负荷有功出力，如果没有达到迭代次数，则返回第四步。

4 算例分析

本文在IEEE 33节点配电系统基础上构建了含有分布式发电、储能以及负荷接入的配电网模型进行仿真分析，如图2所示。该系统有33个节点，32条支路，5条联络开关支路，选取基准电压Ub=12.60 kV,三相功率基准值SB=10 MVA,网络总有功负荷5 082.16 kVA，在节点3、30分别接入容量为1、0.5 MW的分布式光伏电源，在节点16、26分别接入容量为1、1.5 MW的分布式风力电源，节点17接入储能系统。设置仿真步长为15 min，一个调度周期为24 h共96个时段，一个仿真步长中分布式电源和负荷出力是不变的。

图2 IEEE节点配电系统结构图

在实时调度中，风机、光伏以及基础负荷出力是重点。某日配电网中风机、光伏与基础负荷出力预测值如图3所示。

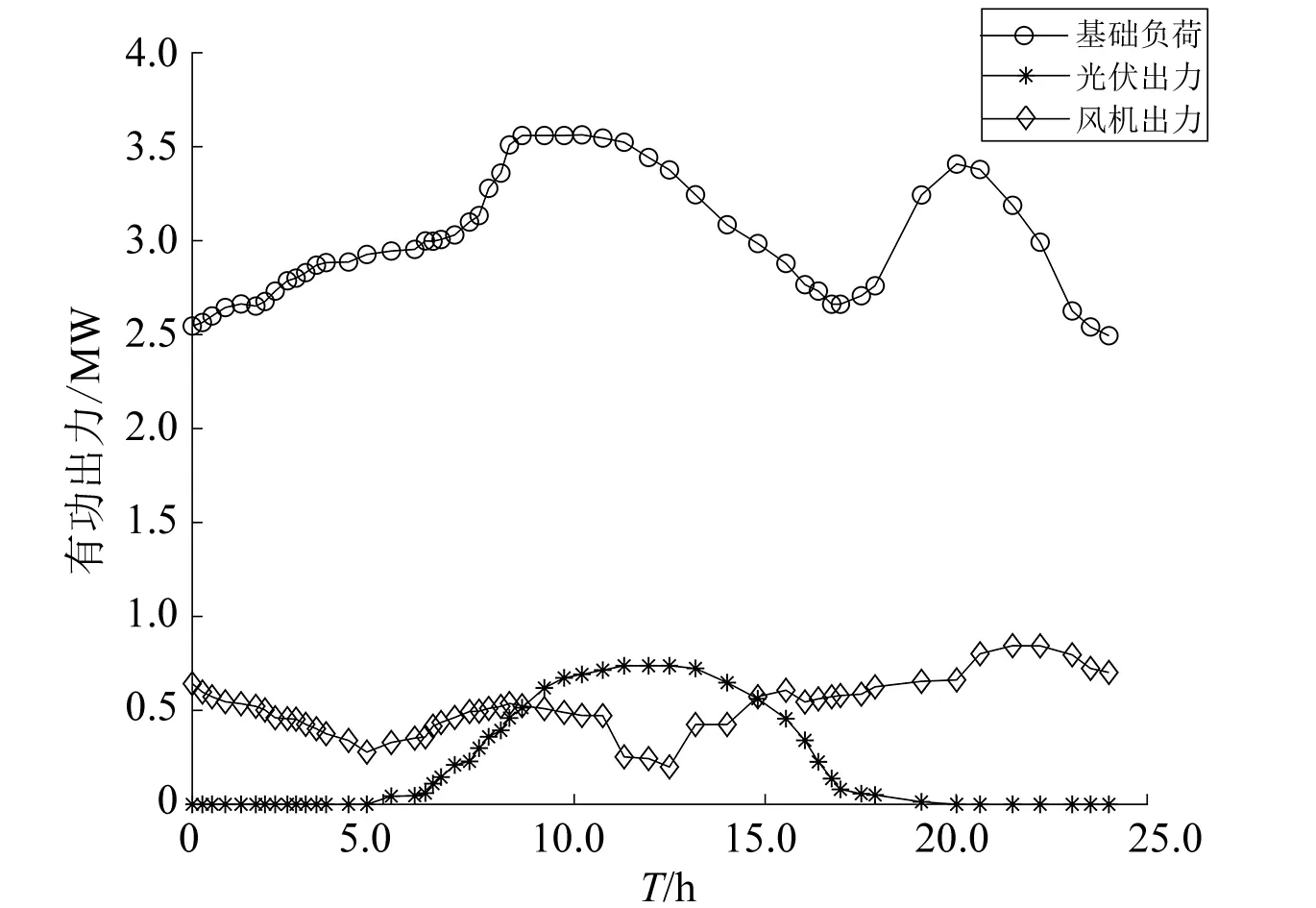
图3 风机、光伏与基础负荷出力预测值

由图3可知，光伏出力随机性和波动性较弱。与光伏相比，风电接入量更大，波动性更强，随机性更大，对配电网有着更强的扰动性。基础负荷出力相对稳定，波动性不大。

为了验证模型的有效性和经济性，设置了3个优化场景进行比较。

场景1：“源-储”协同优化。

场景2：“源-荷”协同优化。

场景3：“源-网-荷-储”协同优化。

场景1忽略可控负荷的参与，考虑系统在实时调度阶段的综合负荷情况，直接设置储能系统的充放电出力，“源-储”协同优化结果如图4所示。

图4 “源-储”协同优化结果

场景2忽略储能系统的参与，负荷以签订合同的方式参与调度，负荷响应调度安排以合同中单位时刻可调用负荷容量为准，每个时刻调度的合同不同，负荷响应调度也不同，“源-荷”协同优化调度结果如图5所示。

图5 “源-荷”协同优化结果

场景3“源-网-荷-储”协同互动，包括分布式电源、网络、可控负载和储能系统，综合考虑其优化效果，如图6所示。

图6 “源-网-荷-储”协同优化结果

由图4～图6可以看出：

(1)场景1中储能系统受到荷电状态约束不能及时削减负荷，负荷的波动较大，当及时充电之后，降低了负荷的波动性。

(2)场景2由于没有储能的参与，再加上可控负荷的调度成本较高，参与调度的可控负载大多为可削减负载，削减了综合负荷有功功率的峰值，与优化前的实际值相比，优化后的幅值曲线波动较低。

(3)场景3的可控负荷仍然以可削减负荷为主，削峰填谷作用在3个场景中最明显，是3个场景中优化效果最好的。

5 结束语

本文对于配电网中“源-网-荷-储”协同优化问题，采用了实时优化的优化调度策略，通过建立双层模型，运用GA-RWPSO对模型进行求解，能够更快速、准确地找到最优解，实现配电网的综合优化调度。同时将该算法应用于IEEE 33节点中进行验证，对比分析了不同场景下协同优化的差异性。结果表明，基于双层模型的“源-网-荷-储”协同优化效果最佳。