轿车车窗上升过程振动响应及噪声仿真

李文平，何川林，张 帅，陈 朝，田亚坤

(燕山大学 车辆与能源学院， 河北 秦皇岛 066004)

0 引言

随着人们生活品质的提高，汽车消费者对汽车车内听觉舒适度的要求也逐渐提高。车窗升降系统作为一个日常用车中被频繁操作的系统，其NVH(noise vibration harshness)性能对车内听觉舒适度有十分重要的影响[1]。目前，各主机厂对车窗升降系统噪声的控制主要是在有试制车之后，通过试验测试分析产生噪声的原因[2]，再反馈到设计部门做优化，这种方法耗时耗力。为避免车窗系统噪声控制过程中烦冗的噪声测试再优化的过程，本文通过对车窗上升过程进行结构动力学仿真和声学仿真，探究了无实车阶段对车窗系统噪声进行预测的方法。

目前已有学者对车辆各子系统NVH性能预测做了大量的研究。赵业淼等[3]对发动机进行多体动力学仿真，得到频率响应结果；将频率响应结果导入发动机有限元模型作为激励，计算出了发动机的激励位移响应；通过声学仿真软件建立发动机边界元模型，导入激励位移响应，计算出了发动机的声压分布，贡献量分析得出油底壳声压贡献量最大，对油底壳进行结构优化成功地降低了发动机总体辐射噪声。Copiello等[4]建立了排气管道的声学有限元模型，在声学软件中定义了一个标准声源振幅，对排气管道模型进行了准确性验证并计算了其声传递损失；再以试验测出的发动机噪声为声源，计算得到了排气噪声响应；分析了排气管道几何形状及内部多孔材料对排气噪声的影响。王欢等[5]建立商用车驾驶室有限元模型并求解其自由模态，与试验自由模态进行对比修正了驾驶室有限元模型；运用Virtual Lab软件建立驾驶室声学仿真模型，采集各内饰部件的声阻抗参数导入模型作为边界条件，将试验采集的驾驶室悬置点加速度作为模型激励，仿真计算出驾驶室声学响应；通过板件贡献量分析确定了噪声贡献最大的板件，通过添加自由阻尼层有效地降低了驾驶室内声压级。Jean-Dupont等[6]对电动汽车的电机噪声进行了研究，根据麦克斯韦原理计算了由电磁现象引起的激励力，通过电机结构动力学仿真得出此激励力下电机的振动响应；将电机振动响应导入声学仿真模型作为边界条件计算出了电机噪声，并对其进行了准确性验证；在此基础上，对电机模型进行缺陷验证，得到了电机结构缺陷对电机辐射噪声的影响。

本文在前人研究基础上提出了一种通过结构动力学仿真及声学仿真在车型开发数模阶段预测车窗上升过程NVH性能的方法。通过对密封条进行单轴拉伸试验及CLD(压缩载荷)试验，仿真修正了密封条的有限元模型；以试验采集的玻璃升降电机本体振动加速度为激励[7]，建立车窗上升过程的动力学仿真模型，从仿真结果中提取内板对标点的振动加速度与该处试验值进行对比，验证了动力学仿真模型的准确度[8]；将车门系统上所有节点的仿真振动加速度导入声腔模型中作为边界条件，导入试验测出的升降电机本体噪声为声源，建立车窗上升过程声学仿真模型，从仿真结果中提取主驾左耳处声压响应与该处试验值进行对比，验证了声学仿真模型的准确性。

1 密封条有限元模型

1.1 密封条单轴拉伸试验及本构模型拟合

本文考虑导槽密封条和水切密封条与玻璃的摩擦振动响应，需要对密封条进行精准建模[9]。密封条的材料是三元乙丙橡胶，为超弹性材料，其应力和应变的关系需用应变能函数进行描述[10]。

根据国标《GB/T528—2009》用万能材料试验机进行密封条单轴拉伸试验，将密封条原件用裁刀裁成哑铃状，用测厚计测量其厚度，用打标器标定试验段长度为25 mm，将制成的密封条样件对称地夹持在试验机上、下夹持器上，夹持位置如图1所示。

图1 密封条单轴拉伸试验装置图

试验过程中，设置拉伸长度为25 mm，即变形率为100%，反复拉伸试样20次以消除Mullins效应[11]，第21次将试样拉断。若试样在标定段内被拉断，则作为试验结果，反之，则重复进行试验。5组有效试验数据中，在一致性较好的几组中任选一组作为最终试验结果，见表1所示。

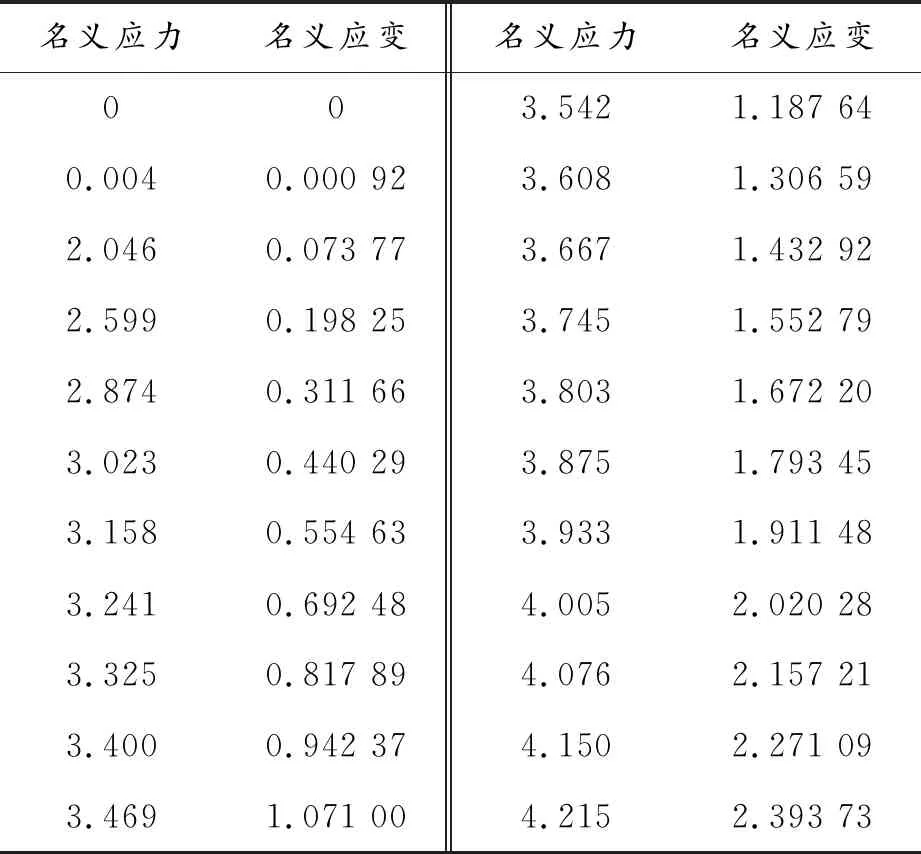
表1 名义应力-名义应变

将表1中的试验数据导入Abaqus软件中进行密封条本构模型的拟合[12]，材料类型选择超弹性材料，试验数据类型选择单轴拉伸试验数据。

拟合得出Ogden3阶模型和MARLOW模型与试验数据相关性较高，拟合结果如图2所示。

图2 本构模型拟合曲线

1.2 密封条压缩载荷(CLD)测试

根据标准QCT 710—2004用万能材料试验机对密封条进行压缩载荷测试。从密封条原件上截取长度为(100±2)mm的5个试样，将试样固定在试验机下工装的上表面，使之与上工装压板平行，保证试验中所施加的载荷作用线与试样的中心线一致，安装位置如图3所示。

图3 密封条CLD试验装置图

试验之前，手动调整试验机上压板至接近密封条上部但不接触的状态，设置下压速度为 30 mm/min，密封条压缩量为4 mm时停止压缩。共进行5组试验，在一致性较好的几组中任选一组作为最终试验结果。

1.3 密封条有限元模型标定

密封条与玻璃之间为摩擦振动，两者刚度相差很大，振动主要由密封条单元微小且急速地蠕变产生，根据工程经验进行橡胶材料摩擦振动有限元仿真时，需要精度极高的橡胶有限元模型。本文通过密封条CLD仿真并与试验值对比来确定影响其模型精度的各项因素，这个过程即对密封条有限元模型的标定。

根据密封条CLD测试样件的实际几何尺寸及约束建立密封条CLD仿真有限元模型，见图4所示。

图4 密封条有限元模型

密封条材料为拟合得出的超弹性材料本构模型，模型底部为全约束固定，调整压板单元的位置至刚要接触密封条的状态，对压板施加垂向30 mm/min的速度，仿真时间设置8 s，即压缩位移为4 mm。提取压板上的压缩反力，此压缩反力即密封条的CLD值。

影响密封条有限元模型精度的主要因素为材料本构模型、密封条单元类型、密封条和压板的单元尺寸。本文拟合得出的密封条本构模型为Ogden3阶模型和MARLOW模型；Abaqus软件中超弹性材料的单元类型为杂交单元，由于所能提供的参数限制，单元类型只能在C3D8H、C3D8RH、C3D8IH中选择。根据工程经验密封条单元尺寸选择0.5 mm，压板单元尺寸为1 mm。

分别将2种本构模型和3种单元类型组合代入密封条CLD仿真模型中，计算得出6种情况下的密封条仿真CLD值。将试验CLD值与仿真CLD值对比，得出当密封条本构模型为Ogden3阶，结构单元类型为C3D8IH的情况下，密封条CLD仿真值与试验值误差最小，见图5所示。

图5 CLD仿真值与试验值曲线

由图5中可以看到：最大误差百分比为8.3%，压缩位移在3 mm以下时，仿真值与试验值的误差很小，玻璃与密封条的压缩距离一般为2.5 mm，因此可以认为该密封条有限元模型能用于车窗上升过程动力学仿真分析。

2 车窗系统动力学仿真模型

2.1 升降电机本体及内板对标点振动加速度采集

玻璃升降电机通过3个安装点固定在车门内板上，电机运行过程中，其本体振动通过3个安装点对车门内板持续激励，本文通过试验采集升降电机本体振动加速度作为车窗系统动力学仿真模型的激励[13]为验证所建动力学模型的准确性，在车门内板上远离电机安装点处确定一点为对标点。通过试验采集玻璃上升过程中对标点的振动加速度，将对标点的振动加速度试验值与仿真值进行对比用以指导动力学仿真模型的修正和准确度验证。对标点振动测试位置及仿真值提取位置见图6所示，仿真值提取点节点编号为1886747。

图6 对标点位置示意图

运用LMS信号采集系统和三向加速度传感器分别采集车窗上升过程升降电机本体和车门内板对标点的振动加速度[14]。

2.2 建立车窗系统有限元模型

车窗系统主要包括车门钣金、车窗玻璃、车门内饰板、导槽密封条及水切密封条，将上述部件运用hypermesh软件进行网格划分，车门钣金用8 mm的壳单元模拟，车窗玻璃和车门内饰板用 6 mm的壳单元模拟，密封条用0.5 mm的六面体实体单元模拟。建立的车窗系统有限元模型见图7所示。

图7 车窗系统有限元模型示意图

模型中的连接关系主要有焊点、焊缝、粘胶、螺栓，其中焊点用faster类型中的CONN3D2单元模拟；焊缝用beam类型中的COUP_KIN单元模拟；螺栓用rbe2单元模拟；胶粘用六面体单元C3D8/C3D6模拟，需保证六面体单元节点与连接钣金壳单元节点对应。

2.3 仿真参数及边界条件的设置

车窗玻璃在正确的安装位置时，密封条唇边对玻璃有夹持作用，本文在Abaqus软件中使用2个分析步来保证玻璃处于正确安装状态，step1对密封条施加微小的压力使其唇边张开，step2释放唇边压力使密封条唇边自动回弹与玻璃接触，该过程完成了玻璃与密封条的正确装配，在此状态下密封条对玻璃有预压力，如图8所示。

图8 玻璃与水切密封条装配示意图

车门通过铰链和门锁与车身相连，车门边缘其他部分则是通过车门密封条与车身密封条弹性接触，仿真模型中通过约束车门铰链和门锁处的3个平动自由度和3个转动自由度来固定车门系统[15]。车窗玻璃上升行程位移为425 mm，上升时间为3.1 s，本文考虑车窗玻璃匀速上升，对车窗玻璃施加位移约束，使其在3.1 s的时间内上升到指定位置。仿真中将试验采集到的升降电机本体振动加速度激励通过安装点输入仿真模型。

2.4 计算结果分析及模型验证

仿真计算得出车窗上升过程车门系统上所有节点的振动加速度。车门法向振动加速度响应云图如图9所示。

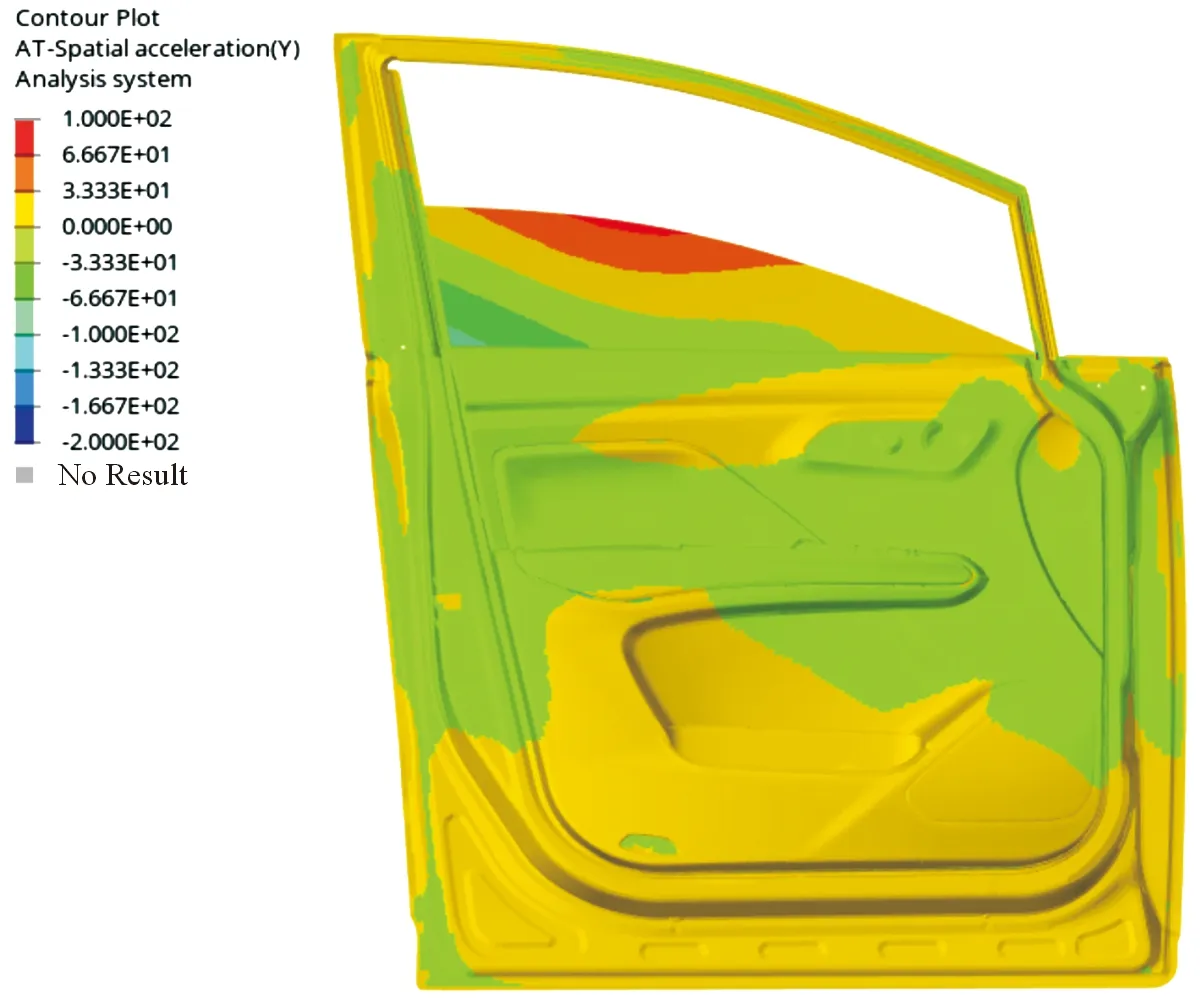
图9 车门振动加速度响应云图

为验证动力学仿真模型的准确度，在仿真模型中提取内板对标点处的振动加速度仿真值与试验值，如图10所示。

图10 振动加速度仿真值与试验值曲线

由图10可以看出，仿真值与试验值在趋势上较为一致，在幅值上有一定的误差，计算得出振动加速度平均误差为8.9%。由于建立动力学仿真模型时对模型进行了简化，去掉了对结构刚度影响不大且自身振动较小的零部件，因此出现误差是合理的，可以认为该模型正确。

3 车窗系统声学仿真模型

3.1 升降电机单体及主驾左耳处噪声测试

本文考虑结构振动噪声，将升降电机近场噪声测出，以噪声源的形式输入声学模型中与结构网格做声振耦合分析。运用LMS信号采集系统和声学麦克风对升降电机近场噪声进行采集[16]，得到升降电机单体噪声信号。

为验证声学仿真模型的准确性，运用人工头信号采集系统采集车窗玻璃上升过程中主驾左耳处的噪声信号[17]，通过信号处理软件计算出该处噪声信号的声压级曲线，后续用来进行声学模型准确性对标。

3.2 仿真模型搭建及边界条件设置

将包含车窗系统网格节点振动信息的动力学仿真结果导入声学仿真软件中，基于动力学结构网格建立声学耦合面，将结构网格上的振动信息映射到声学耦合面上[18]。声学耦合面为结构网格的包络网格，其网格尺寸大小依据求解的最高频率确定，一般要求一个波长包含6～8个网格，网格尺寸计算公式为

(1)

式中：λ为波长，m；c为空气域声速，m/s；f为求解的最高频率，Hz；L为声学耦合面单元尺寸，m。 车窗上升过程的噪声主要集中在4 000 Hz以内，根据式(1)计算得出L为0.014 m。

考虑车窗上升过程中车内的声学响应，建立四分之一车身的声腔有限元网格，声腔网格的尺寸要求与声学耦合面网格要求一致。在声腔有限元网格的外表面上定义声学无限元边界面，即声波可以无反射地穿过该边界向外自由扩散。建立的声学仿真模型如图11所示。

图11 四分之一车身声学仿真模型示意图

将动力学仿真得到的振动响应结果导入模型定义振动声源，将试验测出的升降电机单体噪声导入模型定义点声源。声腔中主驾左耳处设置为声学响应输出点，求解模型4 000 Hz以内的声学响应。

3.3 仿真结果分析及验证

声学仿真计算得出车窗上升过程中四分之一车身内部各处的声学响应，车窗玻璃平稳运行时的声压云图如图12所示，可以看到声压级在50 dB附近变化，与试验结果相符。

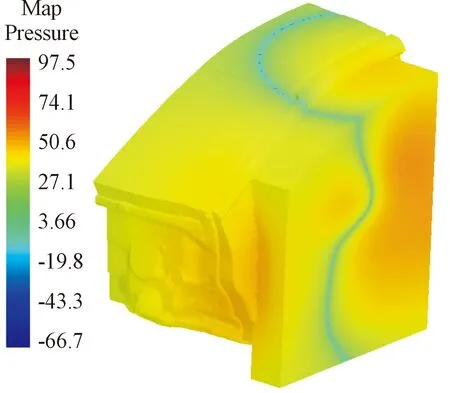
图12 四分之一车身声压云图

从声学响应输出点提取车窗玻璃上升过程主驾左耳处的声压级仿真值与试验值[19]，如图13所示。

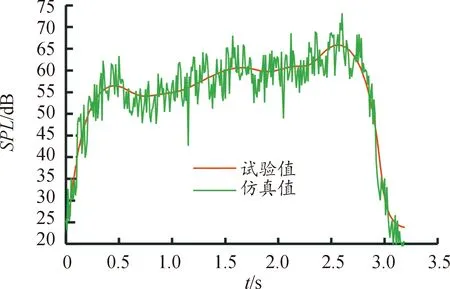
图13 主驾左耳声压级仿真值与试验值曲线

从图13中可以看出仿真值与试验值趋势一致，但有一定的误差。由于进行声腔建模时，去掉了车内所有零部件，没有考虑零部件及汽车内饰的声反射问题，将声腔作为自由场进行计算。计算得出平均声压级误差在10%以内，考虑到模型的简化可以认为仿真结果正确，模型能对车窗上升过程产生的噪声进行有效预测。

4 结论

通过试验和仿真结合的方法标定密封条，得到了准确的密封条有限元模型；建立了车窗上升过程的动力学仿真模型并进行了验证；以动力学仿真结果为振动声源，以升降电机本体噪声为点声源，建立了声学仿真模型，仿真计算得到了车窗上升过程中主驾左耳处的声压变化曲线。结论如下：

1) 对密封条进行拉伸试验拟合出本构模型，通过密封条试验CLD值与仿真CLD值对比标定密封条有限元模型，得到较为准确的密封条有限元模型。

2) 对车窗系统进行简化并建立了车窗上升过程的动力学仿真模型，误差在合理范围内，其仿真结果对车门系统的结构设计有一定的参考价值。

3) 通过对车窗上升过程进行动力学和声学仿真，得到了主驾左耳处准确的声压响应，运用该方法可以在车型开发前期预测车窗升降系统的NVH性能，节省开发成本。