基于博弈论的车辆转向与驱动稳定性协同控制

陈亚伟，甘桦福

(1.汽车噪声振动和安全技术国家重点实验室， 重庆 401122；2.中国汽车工程研究院股份有限公司， 重庆 401122；3.柳州铁道职业技术学院， 广西 柳州 545616)

0 引言

近年来，以线控底盘为基础的主动安全技术得到了快速发展，多种电控系统得到了广泛应用[1-2]，如防抱死制动系统(ABS)、电动助力转向(EPS)、牵引力控制系统(TCS)、主动前轮转向(AFS)、差分制动系统(DBS)等，可以有效提高不同紧急情况下的车辆安全性和稳定性。然而，这些基于转向或基于驱动/制动的主动控制系统大多是独立设计和实现相关功能，每一个主动控制系统都是为了解决一个特定的问题而设计的，没有考虑其他共存系统相互耦合影响。因此，不同主动控制系统之间可能会产生冲突，例如，基于转向的稳定控制系统(AFS)，在车辆遇到紧急情况时会产生额外的转向角度来避免发生碰撞事故。与此同时，存在于车辆上的基于制动/驱动的控制系统(DYC)也会向相应的执行机构发出控制命令，由于没有考虑多个控制子系统耦合影响问题，2个不同的子系统的响应动作最终可能在一定程度上相互抵消，使车辆的主动安全性能有所降低。因此，基于车辆底盘的子系统协调控制成为主动安全控制技术发展的重点[3-5]。

同时，分布式四轮独立驱动车辆具有制动、驱动、转向等执行系统可以独立调节的特点，所以各个子系统的控制形式也更加灵活，如果能实现各个子系统之间的动态交互和协同控制，则这些子系统之间的耦合问题可以被很好的解决，从而能够更好地提高极限工况下的性能。另外，协同控制则可以在全局上整合控制系统、执行机构和传感器等资源，从而消除底盘控制的局限作用，从而有效改善各子系统之间的干涉和耦合，使其协调工作，从而实现整车性能的高度集成化管理和整车性能的最优。所以底盘转向与驱动协同控制对于提高整车的安全性能有着重要的意义。

国外方面，日本Nissan公司提出基于CPU进行信号传输的智能控制技术，对TCS/ABS/4WS及主动悬架进行了集成控制，在一定程度上提高了车辆的综合性能[6]。美国德尔福公司提出了基于顶层观测器的汽车集成控制架构，集成控制了汽车的主动制动和四轮转向系统。德国大陆公司开发的第二代ESP控制系统在发动机干预和差动制动的基础上加入了电控空气悬架系统、主动横向稳定杆和主动转向系统等多种主动控制系统，并通过底盘集成控制器对底盘各个子系统进行协调控制[7]。德国BOSCH公司开发出了车辆动力学管理系统，通过相应的智能控制算法将所需的横摆力矩分配到制动、转向和悬架控制系统中，有效地促进了车辆集成控制技术的发展[8]。He等[9]针对DYC 系统与AFS控制系统的协调控制，提出了一种新的规则将2个子系统的工作区域划分开来，减少了2个控制子系统的耦合作用，减少了制动对车辆纵向动力学的影响，同时提升了车辆在中低侧向加速度时的转向性能和在大侧向加速度时车辆的动力学稳定性。但是，当AFS和DYC在同一工作区间作用时仍然无法避免2个子控制器之间的冲突，所以整车的稳定控制效果在一定程度上仍然会受到影响。

国内方面，主要是采用线性控制、非线性控制和智能控制等方法[10]对车辆底盘子系统进行协调控制。

沈晓明[11-12]建立了分层式协调控制体系，分别通过伺服环路和主环路控制系统实现4WS和LSC的协调控制，其中主环路控制系统分别采用了标准H∞最优控制和混合灵敏度H∞控制进行反馈控制器的设计。在伺服环路主要利用序列二次规划算法实现广义轮胎力的分配。武建勇等[13-14]提出采用线性矩阵不等式(LMI)的H∞控制方法实现四轮转角和DYC的协调控制，提高车辆的操纵稳定性。殷国栋等[15]通过H∞鲁棒控制理论实现4WS和DYC的协调控制，该控制器采用前馈和反馈相结合的方法对理想的线性2自由度模型的理想输出进行跟踪，仿真结果表明该控制策略能有效地降低驾驶员的负担和提高车辆的操纵稳定性。

罗剑[16]利用模型预测控制设计了四轮制动/驱动的协调控制来提高车辆在非线性工况下的横向稳定性。李刚[17]采用模型预测控制算法实现了AFS和DYC系统的集成控制，通过分层式控制结构实现车辆的横向稳定性控制，上层控制器主要通过模型预测控制优化得到车辆的附加横摆力矩和前轮转角，下层控制器分别利用基于规则和优化的驱动力分配方法实现上层控制器的虚拟控制量，进而实现AFS和DYC的协调。宋攀等[18]采用多层次系统设计方法对全线控电动汽车的底盘集成控制器进行设计，在上层控制器中采用滑模控制方法提高车辆的轨迹跟随能力，在底层控制器中，考虑了车体侧倾和俯仰等运动导致的负载转移，采用多边形简化的方法解决轮胎附着极限问题，并通过计算每一车轮的电机力矩和转角来使4个车轮总负荷达到最优。朱茂飞[19]详细地分析了车辆关键子系统之间的耦合机理，并将其具体关系表现在数学模型中，利用非线性解耦控制理论实现ESP和ASS等车辆关键子系统的集成控制，使车辆的操纵稳定性和行驶平顺性得到了提升。

余卓平等[20]从提高车辆响应速度和稳定性的角度出发，分别利用模糊控制和最优控制理论实现车辆的直接横摆力矩(DYC)的分配和车轮的变滑移率控制，最终通过建立参考模型实现制动力分配和变滑移率的协调控制，并提高了车辆的操纵稳定性。卢少波[21]基于对车辆悬架和转向系统之间的侧垂向运动学关系的研究，提出了基于智能模糊控制和灰色预测控制理论对车辆的悬架和转向系统的集成控制策略，来达到提高车辆横向稳定性和舒适性的目标。

博弈理论近年来在控制领域得到了广泛的应用，它主要是用来解决多个体、多系统之间有冲突的决策问题。近年来，博弈论在汽车领域中的应用逐步增多[22-23]。Tamaddoni等[24]将驾驶员模型和横摆力矩控制模块看作2个博弈者来实现无人驾驶车辆路径跟踪系统和DYC的综合控制,这是博弈论在车辆集成控制领域较早的应用。随之，Na等[25]将主动转向系统(AFS)和驾驶员模型看作2个博弈者，从非合作博弈的信息框架下实现驾驶员和主动转向系统之间的交互合作，这是汽车领域较早成功实现人车博弈的一项新技术，在很大程度上提高了汽车的安全性和智能性。国内陈无畏等[26]利用博弈论对汽车转向/制动/悬架等子系统的功能指标进行博弈，从而作为整车集成控制的指标，有效提高了整车控制性能。

由于博弈论适用于解决多个决策者之间的冲突问题，将底盘控制中的多个子系统合作控制问题转化为多个参与者的博弈问题[27]。针对四轮转向系统(FWS)和主动驱动控制系统(ADC)之间的潜在冲突问题，将FWS和ADC视为博弈论框架中的2个参与者，在实际应用中，采用线性二次微分方法处理2个子系统任务分配的冲突问题，以便通过解析和数值求解得到最优解[28-30]。

为了进一步提高车辆的主动安全和横向稳定性，基于博弈论对车辆的转向与驱动协同控制问题进行深入研究，主要的创新点有3个方面：首先，采用博弈论方法处理2个并行的底盘稳定控制系统。其次，采用考虑负载转移影响的加权转矩分配方法对内环进行控制。最后，采用内-外环结构实现了所提出的底盘协同控制方法。

1 全局策略和参考

1.1 全局协同控制策略

本文所提出的协同控制策略全局控制结构如图1所示，它主要由2个控制回路组成：一个外环控制器和一个内环控制器。外环控制器基于博弈论思想，根据驾驶员的输入和车辆/道路情况，计算出期望的横摆力矩和前轮转角。在内环控制器中通过4个独立驱动轮之间的转矩分配来实现对橫摆力矩的控制，所需的转向角度将根据前轮和后轮转向比执行。

注：FWS表示四轮转向；ADC表示主动驱动控制；SBW表示线控转向；DBW表示线控驱动

此外，设计了对比控制器。对底盘控制系统中的FWS和ADC子系统采用线性二次调节(LQR)控制，比较2种控制方法下的车辆主动安全和横向稳定性，以评价所提协同控制策略的有效性。

1.2 车辆动力学模型

控制器设计采用具有横向运动和橫摆运动的单轨模型作为参考模型[31]。选择侧偏角β和横摆角速度γ表示车辆的横向动力学，如下所示。

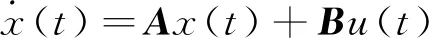
(1)

式中：x=[βγ]T为状态变量，u=δf为前轮转向输入。假设轮胎模型为线性模型，在小转向角情况下保持恒定的纵向速度，则可导出如下常数矩阵：

式中：Cf和Cr分别为前后轴的车轮侧偏刚度；m为车辆质量；Iz为横摆转动惯量；lf和lr分别为质心到前后轴的距离；vx为恒定纵向速度。

2 基于博弈论的协同策略

2.1 外环控制器

根据单轨车辆动力学建立线性二次微分博弈模型[32]，其中2个参与者分别为FWS和ADC。已知初始状态x(t0)=x0时，其状态变量x=[βγ]T，计算表达式为：

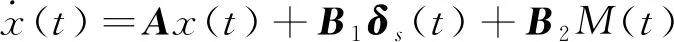
(2)

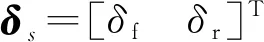
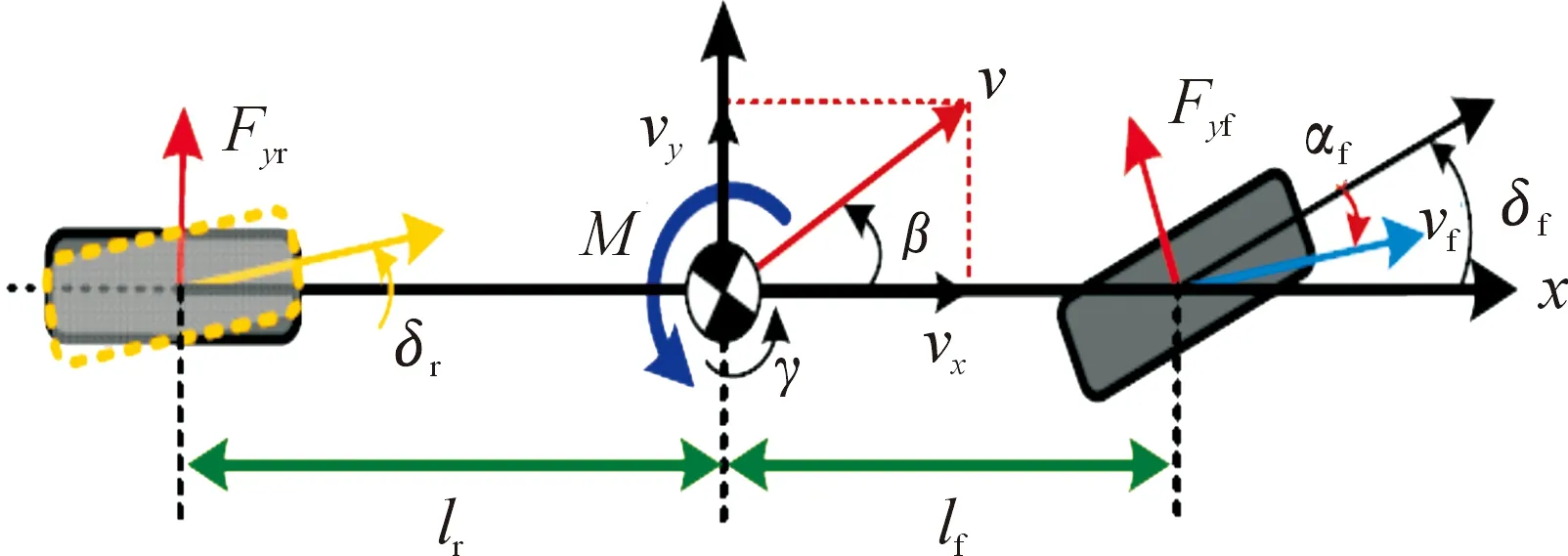
图2 单轨车辆动力学模型示意图

对于每个参与控制者(i=1，2)，二次成本函数为

(3)

式中：对于i=1,2时，有Qi≥0,Rij>0，所有加权矩阵是实对称的。

(4)

式中，上标*表示基于博弈问题的纳什均衡解。

求解线性二次博弈模型，定义哈密顿函数为：

(5)

根据庞特里亚金最小原理，应满足以下必要条件：

(6)

根据式(2)和式(3)定义的线性二次微分博弈策略，可导出一个唯一的开环纳什均衡解，如式(7)所示。

(7)

式中：Li满足耦合的非对称riccati型微分方程，具有自由终态时间和开环结构，如式(8)(9)所示。

L1A+ATL1+Q1-L1C1L1-L1C2L2=0

(8)

L2A+ATL2+Q2-L2C2L2-L2C1L1=0

(9)

式(7)中Φ(t,0)满足如下的转换方程：

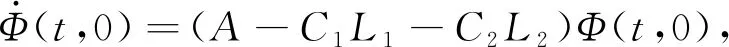
Φ(t,t)=In

(10)

此时，只有当耦合Riccati方程(8)和(9)具有稳定性解并且式(11)中2个正态代数Riccati方程(11)具有对称稳定解时，给定初始状态的纳什均衡解存在。

LiA+ATLi+Qi-LiCiLi=0 (i=1,2)

(11)

在求解交叉耦合的代数Riccati方程(8)和(9)的过程中引入博弈论方法[33]，考虑了FWS和ADC相互耦合对车辆稳定性控制的影响，能够使FWS和ADC这2个底盘稳定性控制子系统协同工作。

为简化计算过程，将前后轮转向角设定为比例关系，即δr=k×δf，其中定义的k可使稳态侧偏角收敛到零，其计算表达式如下[34]。

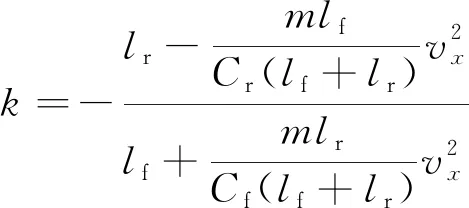
(12)

通过求解上述耦合代数Riccati方程，可以得出基于微分博弈的协同策略控制变量：

(13)

为了说明基于博弈论的控制策略优势，采用基于LQR的控制策略进行比较，其二次成本函数定义如下：

(14)

式中，权矩阵Q、R为实对称，且Q≥0,R>0。假设前后转向角成比例关系，将输入简化为ulqr=[δf,M]T，后轮转向仍由式(12)确定，则最优LQR反馈控制解满足如下形式：

(15)

对于式(1)所示的系统动力学模型，系统常数矩阵Blqr可以转换为：

式(15)中L满足Riccati方程，即有：

LA+ATL+Q-LBlqrR-1BTL=0

(16)

2.2 内环控制器

将横摆力矩M*的转矩分配问题转化为约束优化问题，结合轮胎利用率[35]的概念，将目标函数定义为：

(17)

式中:Tci是分配给第i个轮胎的转矩，i=1,2,3,4分别表示左前，右前，左后和右后。Tci≥0表示驱动，Tci<0表示制动。Fzi是每个车轮的法向载荷，0≤ξi≤1是权重系数，λ是道路附着系数，r是车轮有效半径。其目的是通过仅假定纵向轮胎力来实现外环控制器中导出的期望横摆力矩M*，以最大程度地减少轮胎的使用。

式(17)函数优化目标为在仅考虑轮胎纵向力的情况下使轮胎利用率最小化，以实现外环控制器中所需的期望横摆力矩M*。

车轮转矩应满足以下约束条件[36]：

(18)

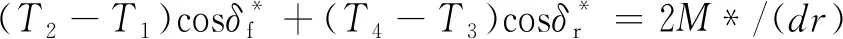
(19)

|Ti|≤min(λrFzi,Tmax)

(20)

式中：d是轴距;Tmax是轮内电动机可以提供的转矩峰值。为了简化和减少变量，根据等式(18)和(19)，可以分别用T4和T1表示T2和T3：

(21)

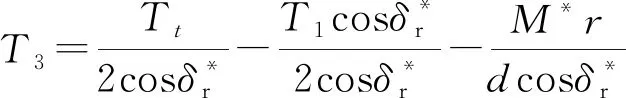
(22)

将目标函数式(17)变换为：

(23)

为了简化和便于计算，将同一侧车轮分为一组，每一侧车轮都视为一个单轨模型。因此，分别推导Jc1和Jc2相对于T1和T4的正定函数，则最优解可推导为：

(24)

(25)

权重系数ξi(i=1～4)根据横向荷载转移确定[11]，假设每一边有相同的权重，即ξ1=3和ξ2=4。

分配给其他2个车轮的转矩可根据式(21)(22)计算，与分配转矩相对应的每个车轮正常载荷可以通过以下公式计算[37]：

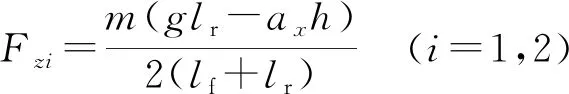
(26)

(27)

式中：h为车辆质心高度；ax为纵向加速度，可以直接测得。假设为单轨模型仅需考虑车辆纵向动力学。

由于实际情况并不一定满足式(18)(19)(20)的约束条件，当上述最优问题无解时，转矩分配将简化为简单的比例分配策略，即除了式(18)(19)(20)的基本约束外，每个车轮的转矩分配正比于每个车轮的法向载荷，满足以下方程式[38]：

(28)

结合式(18)(19)(20)(26)(27)(28)，按比例分配的车轮转矩可推导为[39]：

(29)

(30)

3 仿真结果及其分析

通过与CarSim/Simulink的联合仿真验证了该协同控制方法的有效性。在初始速度为80 km/h的低附着系数路面上进行了双移线工况测试(DLC)，CarSim中内置的驾驶员模型用于执行DLC控制操作。仿真主要参数如表1所示。

表1 仿真主要参数

为了验证所提控制策略的性能，设置驾驶员预瞄时间为0.5 s，并将仿真结果与基于微分博弈的控制以及传统LQR控制进行对比。假设同一轴车轮转向角相同，则δf=δ1=δ3,δr=δ2=δ4，如图3所示。

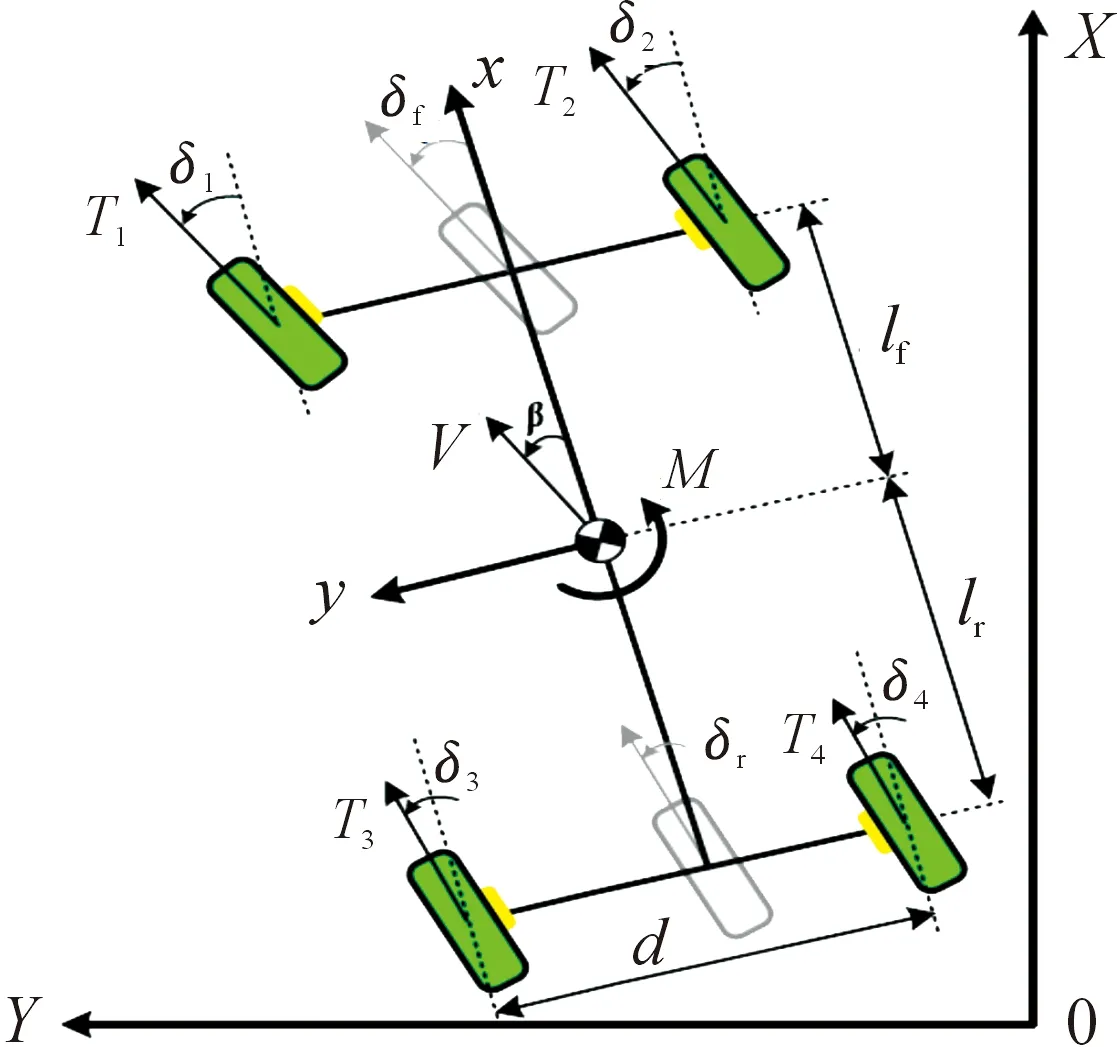
图3 平面运动中的车辆动力学模型示意图

图4为双移线工况(DLC)时驾驶员模型中的方向盘转角曲线。图中DGC表示基于微分博弈的控制方法，LQR表示传统的LQR控制，NoC是指没有特殊控制，只有CarSim内置驾驶员模型施加的转向输入情况。

图4 CarSim中不同控制方法的方向盘转角曲线

由图4可知，DGC和LQR两种情况下的驱动转向输入在幅值上非常相似，相位相差较小。在第一次转弯时，LQR转向系统性能较好，而在第二次转弯时，基于微分博弈的转向系统性能较好。Carsim内置控制条件下，驾驶员模型的输出角度在第一次转弯时变得非常大，表明车辆在双移线工况下已失去横向稳定性。

图5和图6分别给出了不同控制策略下的侧滑角和横摆角速度响应。与驾驶员模型转向角相对应，在没有特殊控制的情况下，车辆会出现较大的侧滑角和横摆角速度响应。而对于基于微分博弈控制和LQR控制的情况，系统仍能保持稳定且响应速度快。相比之下，微分博弈控制的响应幅值比LQR控制的响应幅值要小，在侧滑角和横摆角速度方面，响应相位与驱动模型输入相位基本保持一致。另外，由于2个并行子系统之间合理分配了控制权限，基于微分博弈的控制稳定性优于LQR控制。

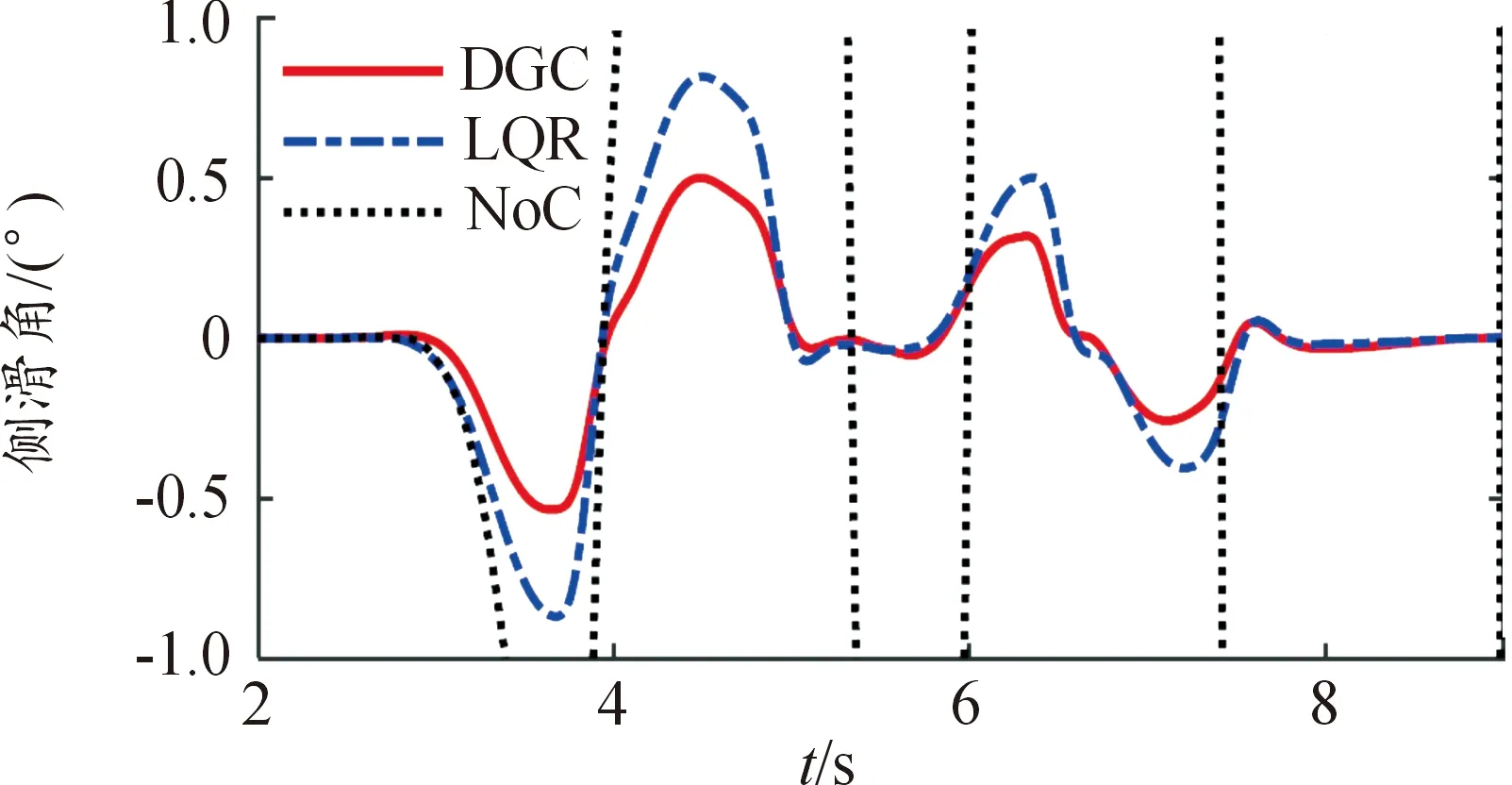
图5 不同控制策略下的侧滑角响应曲线

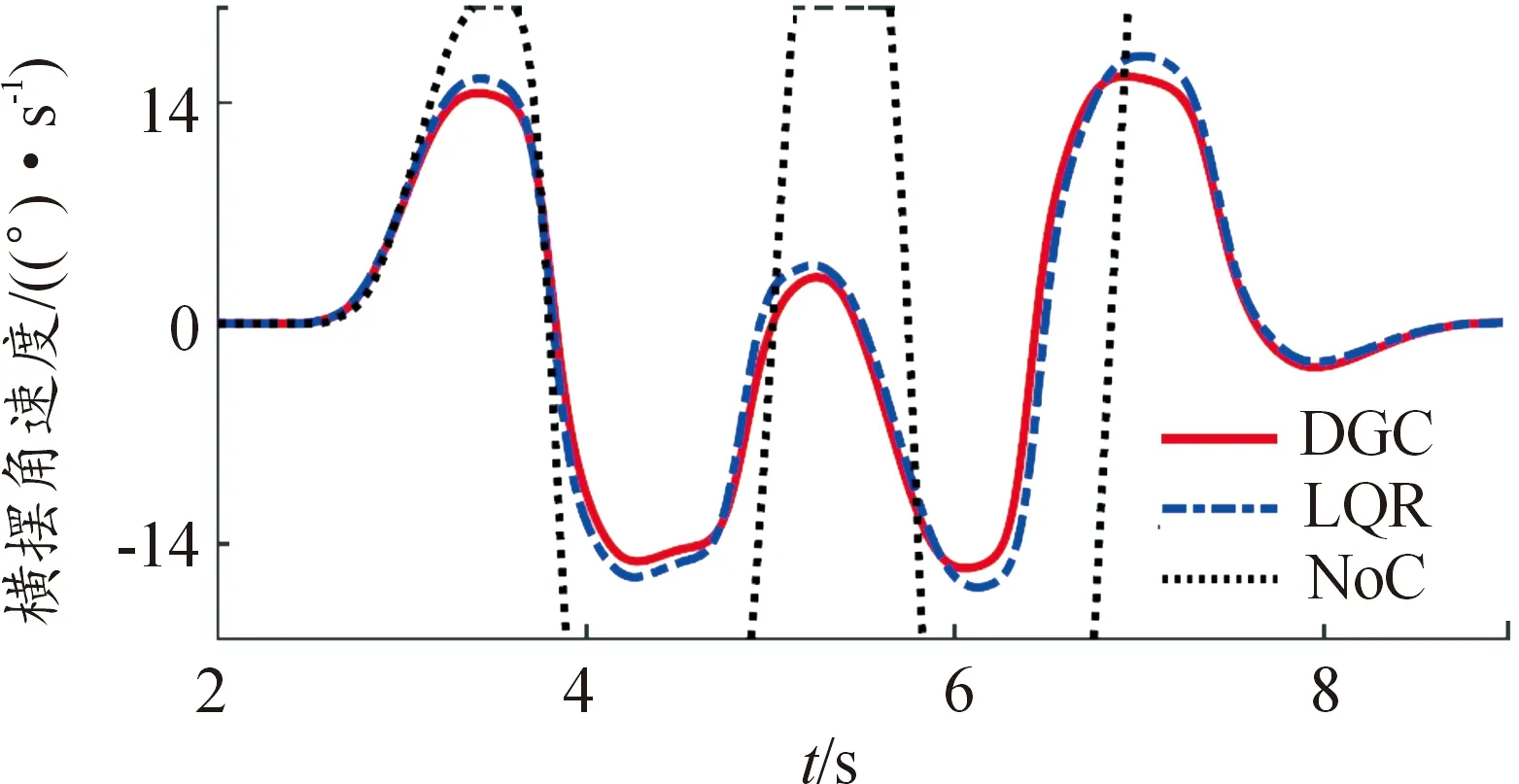
图6 不同控制策略下的横摆角速度响应曲线

图7为可控前轮转向角度曲线。结果表明，与基于微分对策的控制相比，LQR控制具有更大的控制权限。由于后轮的转向角与前轮转向角变化相似，只是振幅略有不同，故图7中仅画出了前轮转向角变化情况。图8显示了前轮和后轮之间的转向角比。由图8可知，相变的特征速度约为59.3 km/h。当纵向速度大于59.3 km/h时，后轮转向角与前轮转向角保持相同的相位。当纵向速度小于59.3 km/h时，后轮转向角与前轮转向角相位相反。

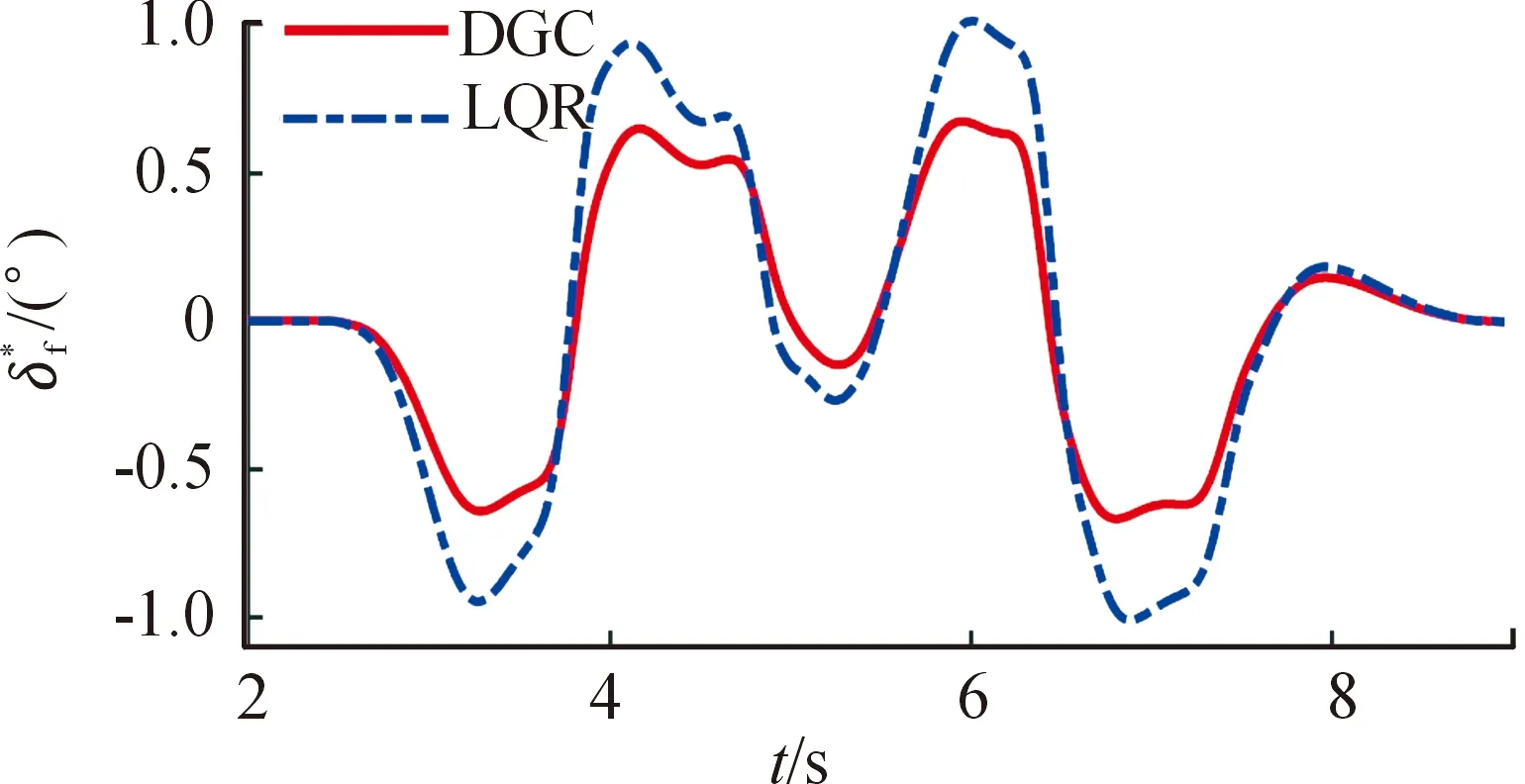
图7 可控前轮转向角度曲线

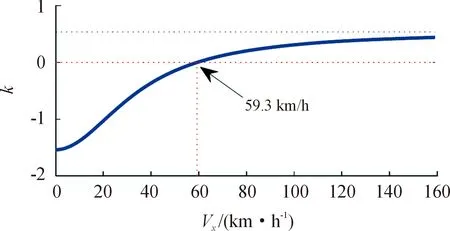
图8 前轮和后轮之间的转向角比曲线

图9为橫摆力矩控制曲线。该控制变量的精准控制将通过外环的主动驱动控制(ADC)系统来实现。显然DGC对M*的控制范围要比LQR大得多，表明在微分博弈控制的情况下，基于ADC的橫摆力矩控制具有更大的权限，横向稳定性更好。

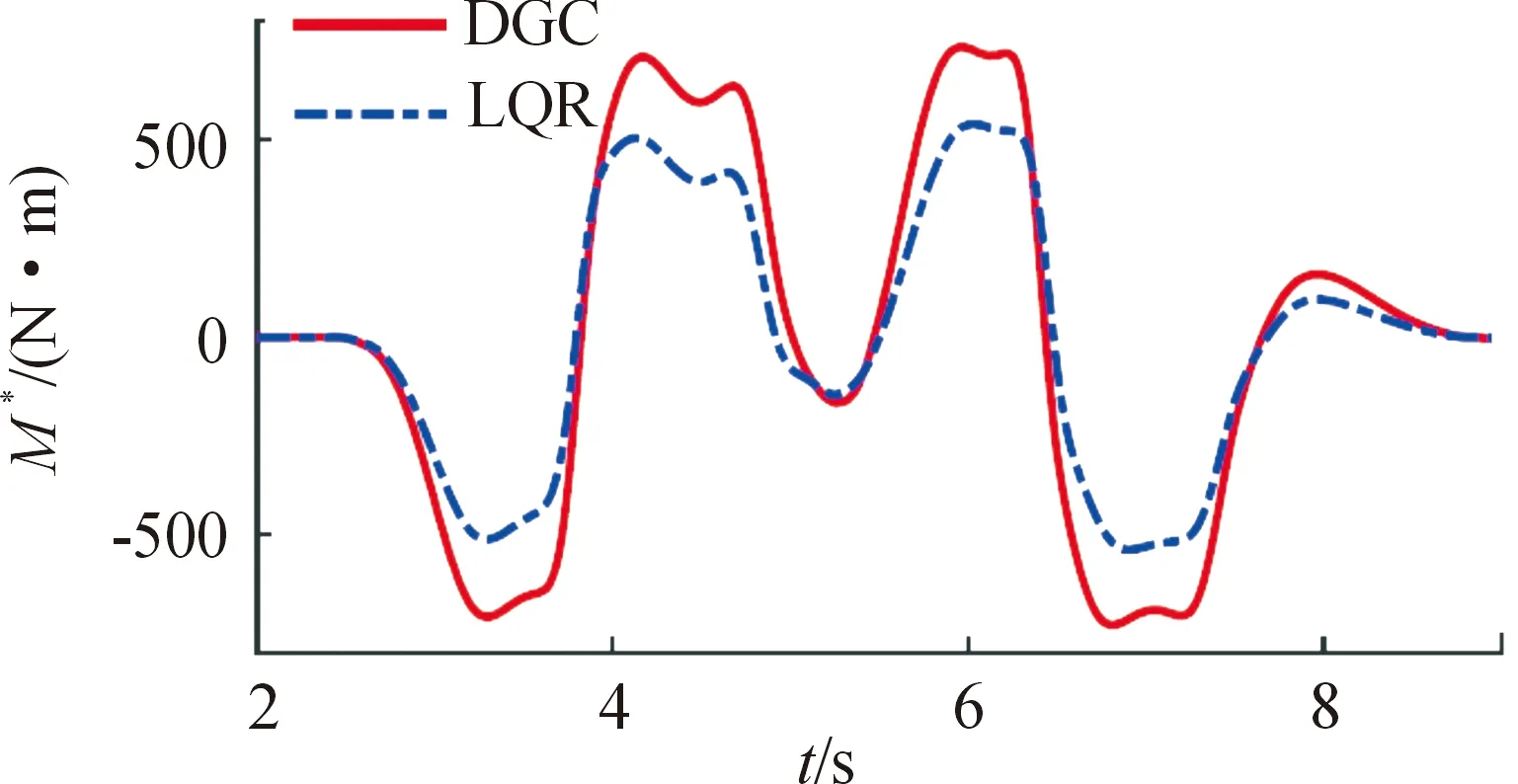
图9 橫摆力矩控制曲线

图10显示了DGC和LQR控制策略下每个车轮分配的驱动力矩。这里，Ti>0表示行驶，Ti<0表示制动。从DGC控制情况下的控制转向角和橫摆力矩可以看出，与LQR控制情况相比，ADC子系统分配了更大的功率。因此，在相同的作用顺序(转矩形状)下，DGC分配的转矩幅值大于LQR分配的转矩幅值。另外，左前轮和右后轮以及右前轮和左后轮均是同步运动的，两组车轮分别通过驱动和制动进行反相位动作，在外环产生合适的修正横摆力矩。

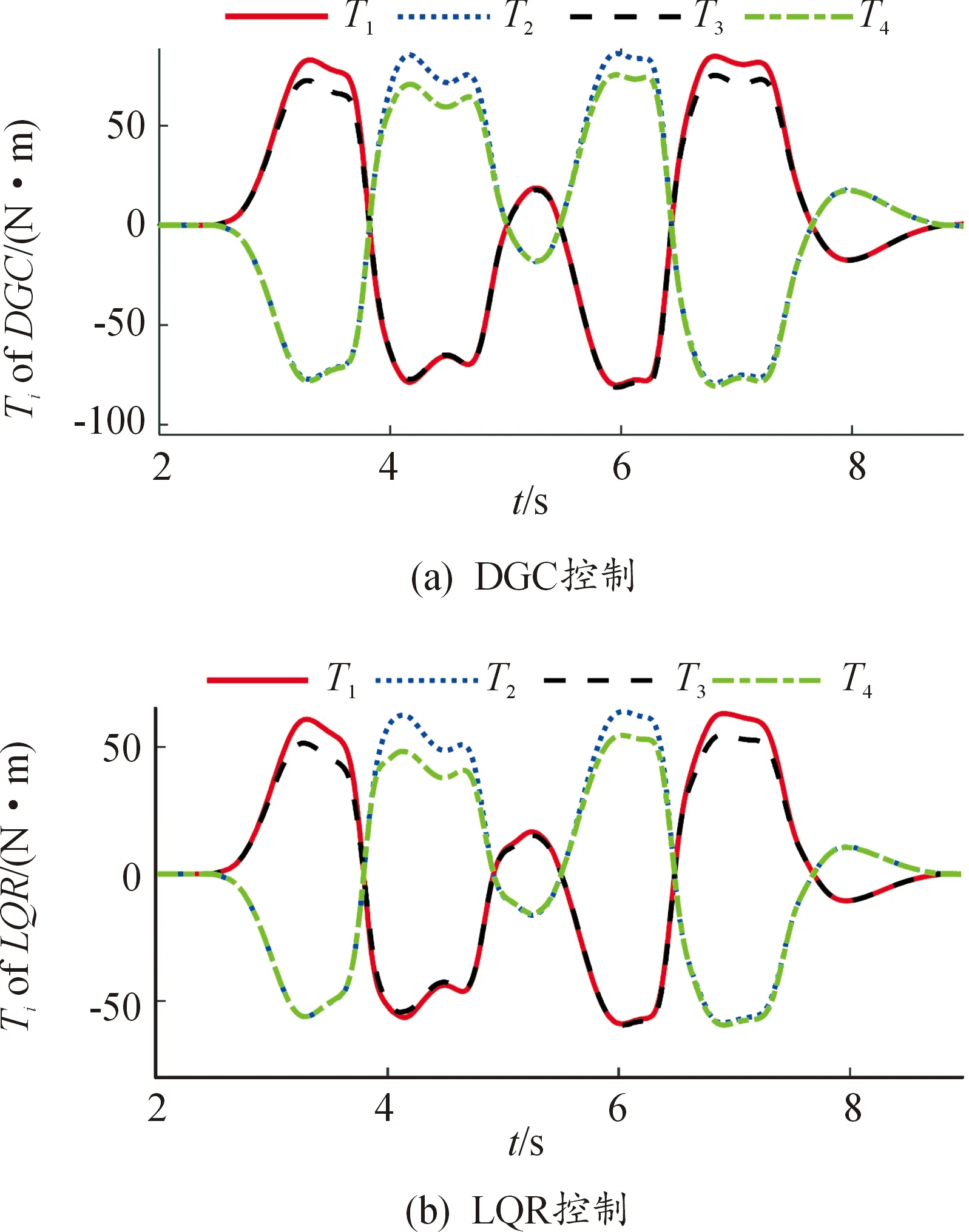
图10 不同控制策略下每个车轮分配的驱动力矩曲线

图11为不同情况下的纵向速度变化曲线。在较大转矩干预下，微分博弈控制对纵向动力学的影响小于LQR控制，说明微分博弈控制(DGC)的稳定性优于LQR控制。

图11 不同情况下的纵向速度变化曲线

图12显示了不同情况下的车辆运动轨迹，BAS表示车辆期望运动轨迹。由图12可知，尽管没有施加特殊控制情况下车辆也可以跟踪所需的轨迹。但是，在没有施加控制情况下，车辆在最终转弯结束之前就超出了预定的车道，这对于实际情况是危险的。对于DGC和LQR控制策略来说，虽然DGC和LQR控制策略都可以确保车辆沿着预定车道行驶，但DGC控制下的车辆可以更准确的沿着期望轨迹行驶，车辆的安全性和横向稳定性较高。

图12 不同情况下的车辆运动轨迹曲线

对图12中的不同控制方法选取均方根误差(RMASE)、平均绝对误差(MAE)、平均绝对值百分比误差(MAPE)、平均均方误差(MSE)以及决定系数(R2)评价控制结果，计算表达式如下：

(31)

(32)

(33)

(34)

(35)

表2为不同控制方法的误差指标对比结果。从表2可知，NoC、LQR以及DGC 3种控制方法中，从控制误差评价指标进行分析，误差由小到大依次为DGC、LQR、NoC，本文提出的DGC控制方法由于考虑了底盘转向子系统和驱动/制动子系统的耦合影响，其控制精度最高，车辆的安全性和舒适性更优越。

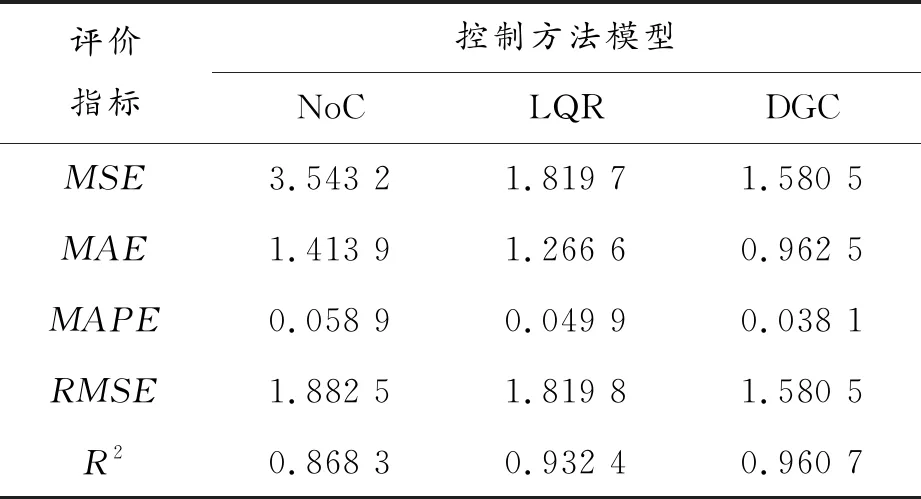
表2 不同控制方法的误差指标对比结果

4 结论

将四轮转向(FWS)和主动驱动控制(ADC)2个底盘稳定系统的协同控制问题转化为具有无限边界和开环信息结构的两者博弈问题，提出了一种多个稳定性控制子系统协同控制策略。

以基于转向控制的FWS子系统和基于驱动控制的ADC子系统分别作为系统的2个博弈者，并与传统的LQR控制方法进行对比，验证了所提出微分博弈控制方法的有效性。通过采用内环加外环控制回路将博弈论的思想引入到协同控制系统中，实现了基于博弈的2种底盘控制系统的协同配合控制。

在CarSim/Simulink的联合仿真环境下，对该协同控制策略在双移线(DLC)工况下的性能进行了测试。仿真结果表明，与LQR控制方法相比，微分博弈控制方法可以对四轮转向(FWS)和主动驱动控制(ADC)进行控制权限分配，有效提高车辆的主动安全和横向稳定性能。