非齐次拟线性双曲方程组Goursat问题解的整体存在性*

窦浩楠, 刘存明

(曲阜师范大学数学科学学院,273165,山东省曲阜市)

0 引言与主要结果

考虑一阶非齐次拟线性双曲方程组

(1)

其中u=(u1,…,un)T是关于(t,x)的未知函数,A(u)是一个n×n矩阵,其中元素aij(u)(i,j=1,…,n)关于u适当光滑,B(u)=(B1(u),…,Bn(u))T是u的已知光滑向量函数.

由严格双曲型方程组的定义,对所考察区域上任意u,A(u)有n个互异的实特征值,

λ1(u)<λ2(u)<…<λn(u).

(2)

设li(u)=(li1(u),li2(u),…,lin(u))(ri(u)=(r1i(u),r2i(u),…,rni(u))T) 是对应于λi(u)(i=1,…,n)的左 (右)特征向量,即li(u)A(u)=λi(u)li(u)(A(u)ri(u)=λi(u)ri(u)),则det|lij(u)|≠0(det|rij(u)|≠0). 在严格双曲型假设下,li(u),ri(u)及λi(u)与A(u)有相同的光滑性. 不失一般性,设

li(u)rj(u)=δij,i,j=1,…,n,

(3)

ri(u)Tri(u)=1(i=1,…,n), 其中δij表示Kronecker符号.

对任意i=1,…,n,若沿着u-空间中过原点u=0 的第i特征轨线u=ui(s):

(4)

成立,∇λi(ui(s))ri(ui(s))≡0, ∀|s|≪1, 即

λi(u(i)(s))≡λi(0), ∀|s|≪1,

(5)

则称式(1)是弱线性退化[1]. 非齐次双曲方程组(1)右端项B(u)满足匹配条件,即过原点的任一特征轨线成立

B(ui(s))≡0, ∀|s|≪1,

(6)

其中ui(s)由式(4)给出.

考虑方程组(1)满足如下条件

u=φ(t):x=x1(t);u=ψ(t):x=xn(t)

(7)

的特征边值问题,其中x=x1(t)及x=xn(t)分别是过(t,x)=(0,0)的第1,n条特征线,即

(8)

(9)

其中φ(t)=(φ1(t),…,φn(t))T,ψ(t)=(ψ1(t),…,ψn(t))T是给定的C1函数,且在(0,0)处满足C1相容性条件

B(φ(0))(λn(φ(0))-λ1(ψ(0)))=b0;φ(0)=ψ(0),

(10)

其中b0=λn(φ(0))φ′(0)-λ1(ψ(0))ψ′(0)+A(φ(0))(ψ′(0)-φ′(0)).

对齐次双曲方程组(B(u)≡0)Cauchy问题已经做了广泛地研究[2,3]. 对Goursat问题(1)及式(7)～(10),在线性退化条件下,当给定的特征边值数据的BV范数充分小时,存在唯一的整体经典解[4]. 在文献[5-7]中作者得到了拟线性双曲方程组Goursat问题的C1解的整体存在性及渐近性态. 这些结果均是对齐次双曲方程组研究的,即方程组(1)无右端项的情况.

本文考虑方程组特征边值问题(1)及式(7)～(10)的光滑解. 在方程组弱线性退化条件及B(u)满足匹配条件下,若给定的特征边值数据W1,1范数充分小,证明了整体C1解的存在性,见定理1.

由双曲方程组特征边值问题C1解的局部适定性理论[8]知,若φ(t),ψ(t)∈C1,并且在(0,0)处满足C1相容性条件,则存在T*>0,使得方程组(1)及式(7)～(10)在DT*≜{(t,x)|0≤t≤T*,x1(t)≤x≤xn(t)}上存在唯一的C1解u=u(t,x). 我们得到如下的C1解的整体存在性.

定理1 假设方程组(1)是严格双曲,弱线性退化,且右端项B(u)满足匹配条件(6). 对于满足C1相容性条件(10)的特征边值φ(t),ψ(t),令

(11)

则存在与M无关的正常数ε>0,当

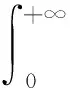
(12)

(13)

时,则问题(1)及式(7)～(10)存在唯一的整体C1解u=u(t,x),(t,x)∈{(t,x)|t≥0,x1(t)≤x≤xn(t)},且对任意t≥0,成立

‖u(t,·)‖C0≤Cε, ‖ux(t,·)‖C0+‖ut(t,·)‖C0≤CM.

(14)

1 预备知识

首先,在正规化坐标下[1],条件(5)与(6)化为

(15)

为整理波分解公式，引入如下引理.

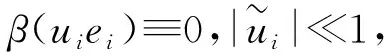
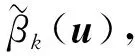
(16)

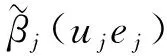
(17)

从而

(18)

下面引入波分解公式[9-11]. 令

wi=li(u)ux,βi=li(u)B(u),i=1,…,n.

(19)

由式(3),得

(20)

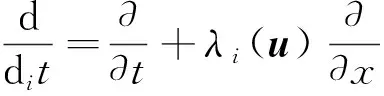
(21)

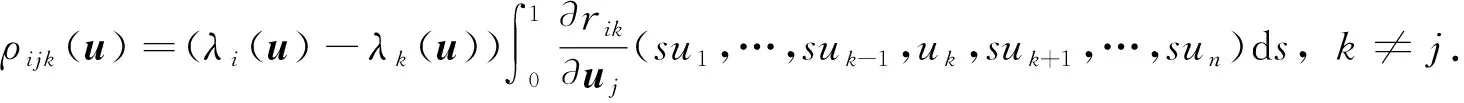
(22)

其中Fijk(u)=ρijk(u)+∇λi(u)rk(u)δij.显然

Fijj(u)≡0, ∀j≠i.

(23)

在弱线性退化条件下,若u是正规化坐标,有

Fiii(uiei)≡0, ∀i.

(24)

由方程组(1)及式(20)得

(25)

对式(25)关于x求导且由式(20),得

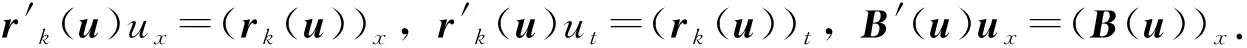
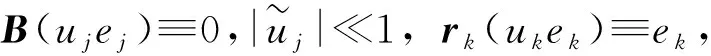
(26)

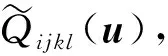
(27)

其中

(28)

从而

(29)

其中γijk(u)=(λj(u)-λk(u))li(u)∇rk(u)rj(u)-λ′i(u)rj(u)δik.在弱线性退化条件下,若u是正规化坐标,有

γiii(uiei)≡0, ∀i.

(30)

2 定理1的证明

不妨假设u=(ui,…,un)T是正规化坐标. 由C1解的局部适定性理论,为证明定理1,只需在C1解u=u(t,x)的任何存在区域上,建立u及ux的C0模一致先验估计即可.

假设Goursat问题(1)及式(7)～(10)的C1解u=u(t,x)满足

|u(t,x)|≤δ.

(31)

要得到u及ux的C0估计,只需对u和w建立C0模估计即可. 由式(2)知,存在足够小的正常数δ1和δ2,使得

λi+1(u)-λi(u)≥δ1, ∀|u|,|v|≤δ2,i=1,…,n-1.

(32)

对任意T>0,在解u(t,x)的存在区域D(T),令

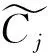
要证明我们的结果,需要下面的引理,其证明见文献[5].

引理2[5]设φ(1)=φ(1)(t,x),φ(2)=φ(2)(t,x)∈C1,分别满足

φ(1)(t,x1(t))=g1(t),φ(1)(t,xn(t))=gn(t),φ(2)(t,x1(t))=y1(t),φ(2)(t,xn(t))=yn(t),

其中λ,μ∈C1且存在正常数δ0,使得μ(t,x)-λ(t,x)≥δ0, 则

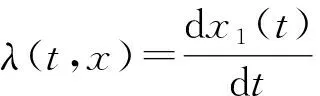
应用引理2,得到QUU(T),QUW(T)及QWW(T)的估计.

引理3 存在正常数C>0,使得

(33)

证明对公式(22)应用引理2,得

其中φ(t),ψ(t)由式(7)定义,F=(F1,…,Fn) 由式(22)给出. 在正规化坐标u下,由弱线性退化条件,对式(24)由Hadamard公式,得

(34)

从而,有

C((1+U∞(T))QUW(T)+QUU(T)).

(35)

由式(13),得

(36)

对公式(27)应用引理2,得

(37)

其中H=(H1,…,Hn)由式(27)给出. 由式(19),得wi(t,x1(t))=li(u(t,x1(t)))ux(t,x1(t)), 再由式(1)及式(7),得

wi(t,x1(t))(λ1(u(t,x1(t))-λi(u(t,x1(t))))=li(φ(t))φ′(t)-li(φ(t))B(φ(t)),i≠1.

(38)

上式关于t在[0,+∞)积分,由式(12),(13)及引理1,得

(39)

(40)

又由式(27)～(28),得

C(QWW(T)+(1+U∞(T))QUW(T)),

(41)

从而

QWW(T)≤C(ε+QWW(T)+(1+U∞(T))QUW(T))2.

(42)

对式(22)和式(27),利用引理2,同理可得

结合式(31),(36)和(42),即证明引理3.

为证明C1解的整体存在性,只需证明如下命题.

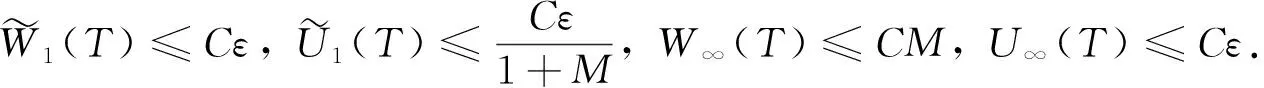
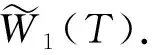
(43)

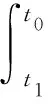
(44)

当j≠i时,将式(32),(34)及(41)代入式(44),得

(45)

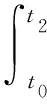
(46)

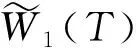
(47)

由式(30)及Hadamard公式,得

(48)

对式(38),由式式(11),式(31)～(32)及引理1,得

(49)

同理,得

|wi(t,xn(t))|≤CM,i=1,…,n-1.

(50)

将式(48)～(50)代入式(47),得

(51)

从而W∞(T)≤CM.

由式(12)、(13),得

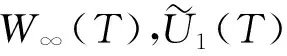
(52)

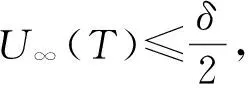
‖ut‖C0≤C‖ux‖C0+C‖u‖C0≤CM.

定理1得证.