基于自适应线性自抗扰控制的飞机防滑刹车系统重构控制
刘舒畅 ,杨 忠 ,张 钊 ,陈 爽 ,张小恺
(1.南京航空航天大学自动化学院,江苏南京 211100;2.航空机电综合航空科技重点实验室电子工程部,江苏南京 211100)
1 引言
具有良好性能的飞机防滑刹车系统(aircraft antiskid braking system,AABS)是成功完成飞行任务的关键,它与飞机和机组人员的安全密切相关[1].随着航空工业的快速发展,对大吨位高速度飞机的需求越来越大,该类型飞机的着陆过程对AABS提出了更高的性能要求[2].此外,AABS是强非线性、强耦合的,并且易受跑道环境在内的许多不确定性因素影响,这使得AABS控制器设计十分具有挑战性[3].
近年来,针对AABS的传统PID+PBM控制方式在有干扰的跑道上制动效率不高,并且伴有低速打滑现象等问题[4],研究者们提出了许多先进的控制方法,如:混合滑移差PID控制[5]、动态面反步控制[6]、最优模糊控制[7]、自学习滑模控制[8]、直接自适应神经网络控制[9]等.文献[10]提出了一种基于非对称势垒Lyapunov函数的控制器,有效地将AABS的运行状态约束在健康区域和轻滑移区域.考虑到AABS在刹车过程中易受不确定性干扰影响,文献[11]设计了一种非线性观测器用于在线估计扰动,并引入了快速终端滑模控制器来跟踪时变的最佳滑移率.上述工作对AABS控制进行了较深入的研究,但却忽视了执行器失效等典型组件故障产生的影响:国内AABS设计主要是基于液压控制系统,较长的液压管道存在油液混入空气以及内泄露危险,如果没有定期维护,很容易引起功能退化甚至失效,这将会导致许多安全隐患[12-13].执行器故障发生后如何保证AABS稳定性以及令人满意的制动性能是目前迫切需要关注和解决的问题.
为了真正提高AABS的安全性与可靠性,一方面可以从硬件层面进行设计和配置[14-15],但是苛刻的硬件测试及实验条件限制了该方法的发展;另一方面,可以将容错控制概念引入到AABS控制器设计中,这也是未来AABS的主要发展方向和急需关注的关键技术[16].重构控制作为容错控制的一个热门分支,目前已被广泛应用于一些安全关键系统,特别是航空航天工程领域[17-18].重构控制实质上是把被控系统可能发生的故障考虑在控制器设计过程中,在系统的元部件或子系统出现故障时,利用故障系统的信息合理地动态配置控制器结构或参数,抑制或消除故障带来的不利影响,进而实现闭环系统渐近稳定和可接受的工作性能.常见的重构控制可以分为以下几类: 自适应控制[19-20]、模糊控制[21]、多模型切换控制[22]、滑模控制[23]以及其他鲁棒控制[24]等.此外,考虑到AABS本身是一个强非线性系统,尤其是内部子系统间又存在耦合,这些都增加了系统精确建模的难度.同时,很多非线性重构控制算法较为复杂,在工程领域实现相对困难.因此,设计一种结构明确、不依赖模型、抗故障干扰能力强且易于工程实现的重构控制器具有重要意义.
韩京清研究员继承了经典PID控制器的精华,提出了对模型精度要求低且易于实现的自抗扰控制(active disturbance rejection control,ADRC)技术[25].ADRC不仅具有控制响应速度快、无超调、可安排过渡过程以及参数适应对象范围大等优点,还能够观测与补偿系统所受内外扰动[26-27].因此,ADRC已被广泛应用于容错控制系统设计[28-30].然而,ADRC需要整定的参数较多,使得实际应用难度增加.随后,高志强教授团队提出了线性自抗扰控制[31](linear active disturbance rejection control,LADRC).LADRC基于线性形式的扩张状态观测器,控制律采用PD线性结构,同时通过“带宽法”整定控制器参数,大大简化了ADRC的结构和参数[32].目前,LADRC已经被应用于多种工程领域[33-35].
针对受执行器故障和不确定性干扰影响的AABS,本文提出一种基于自适应线性自抗扰(adaptive linear active disturbance rejection control,ALADRC)的重构控制方法,旨在保证系统发生故障后的稳定性以及可接受的刹车性能.与现有部分研究成果相比,所提出的重构控制方法主要贡献归纳为如下几个方面:
1) 该控制方法将AABS扩展出了一个新的状态变量,该状态变量是无故障系统描述中未注意到的所有未知动态和干扰的总和,这在很大程度上间接简化了模型;
2) 设计了自适应线性扩张状态观测器和自适应线性状态误差反馈律,利用二者分别对总扰动进行观测和补偿.主要设计思路是结合了智能控制思想,基于BP神经网络,利用状态误差反馈和系统输出信息,在线自动调整观测器和反馈律参数.这不仅减少了手动调参的繁琐,而且大大增强了所提出的重构控制器在面对故障和干扰时的适应性和鲁棒性;
3) 该方法本身是一种鲁棒控制策略,不需要额外的故障检测与识别(fault detection and identification,FDI)模块,并且控制器是自适应的.因此,该方法属于主动重构控制和不依赖FDI重构控制的一种新颖结合,这使得其成为未知故障条件下一种有趣的重构控制方案.
2 飞机防滑刹车系统建模
2.1 飞机防滑刹车系统组成结构及工作原理
如图1所示,AABS主要由以下几部分组成: 飞机机体、起落架、机轮、液压伺服系统、刹车装置、防滑刹车控制器.AABS各子系统之间存在强关联耦合,并表现出强非线性和强复杂性等特征.
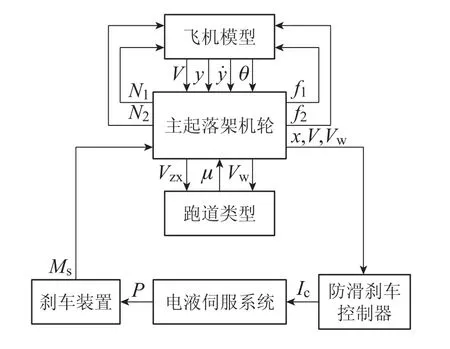
图1 飞机防滑刹车系统组成结构Fig.1 AABS composition structure
AABS工作原理为:飞机着陆后,防滑刹车控制器根据速度传感器提供的机轮速度信息,产生防滑电流控制液压伺服系统产生刹车压力,进而通过刹车装置转换为刹车力矩作用在机轮上使其减速,从而使机轮和地面之间产生相对滑动,由此产生的摩擦力给飞机一个沿纵向向后的力,即结合力.结合力与机轮滚动半径的乘积就构成结合力矩,机轮的转动速度就是由结合力矩和刹车装置产生的刹车力矩来共同控制的.AABS的作用就是在保证不出现深度打滑的情况下,最大限度利用地面的结合力,提高飞机刹车效率,缩短落地滑跑时间与距离.
2.2 飞机机体动力学
根据防滑刹车的实际过程和客观事实,可以做出如下合理假设:
1) 将飞机机身视为集中质量的刚体;
2) 飞机刹车过程中不考虑发动机转子产生的陀螺力矩;
3) 飞机刹车过程中忽略侧风影响;
4) 飞机刹车过程中忽略轮胎变形;
5) 所有受刹机轮的刹车机构性能一致,且同步控制.
飞机机体受力图如图2所示,图中具体参数见表1.

表1 飞机机身动力学参数Table 1 Parameters of the aircraft fuselage dynamics
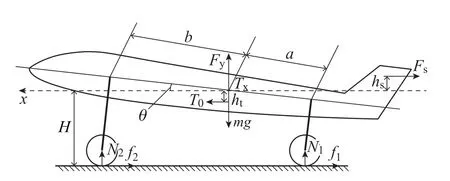
图2 飞机机体受力图Fig.2 Force diagram of aircraft fuselage
飞机纵向运动方程、垂直方向平衡方程和质心力矩平衡方程分别为
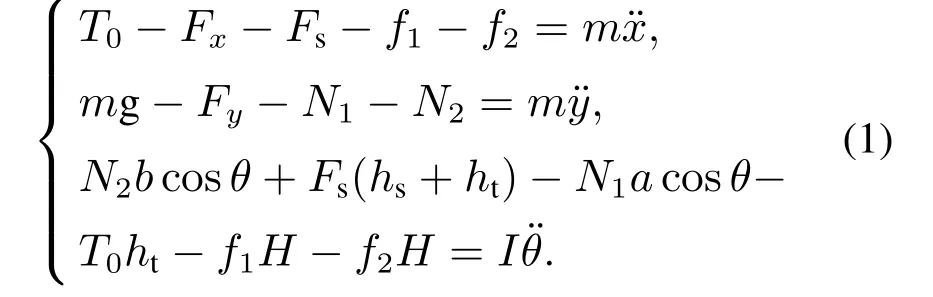
根据空气动力特性影响,可以得到
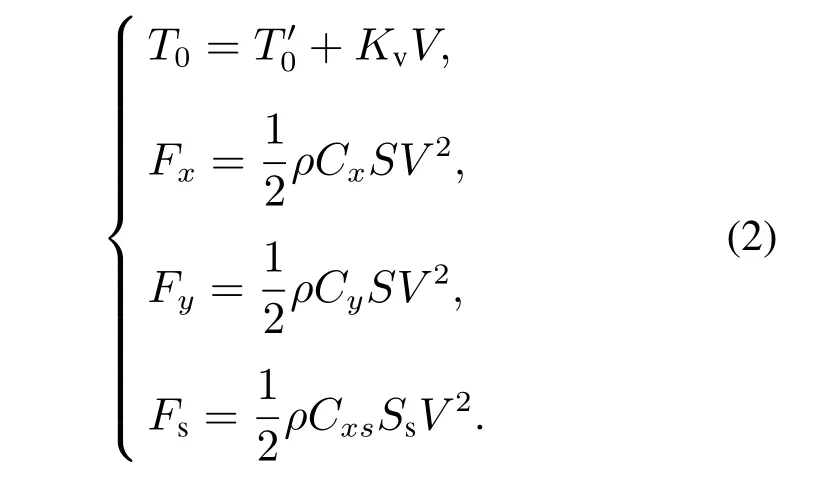
轮胎-跑道结合系数μi定义为

式中i=1,2.
2.3 起落架动力学
起落架的主要功能是支撑和缓冲,用来改善飞机纵向和垂直方向上的受力情况.除了机轮和刹车装置外,支柱、缓冲器和扭力臂也是起落架的主要组成部分.在本文中,假设扭力臂的刚度足够大,并且忽略了机轮相对于支柱和缓冲器的扭转自由度,所以不考虑扭力臂.
缓冲器可以合理地简化为一个质量-弹簧-阻尼系统[36],缓冲器作用在机体上的力可以描述为
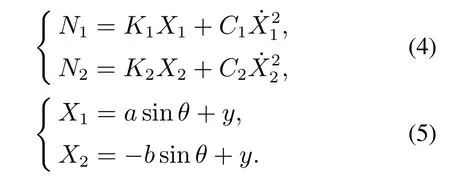
式中参数描述见表2.

表2 缓冲器参数Table 2 Parameters of the buffer
由于起落架和机体之间为非刚性连接,在刹车力的作用下会产生水平位移和角位移.但支柱是悬臂梁,其角位移非常小,可以忽略不计.因此起落架的横向刚度模型可用以下等效的二阶方程表示:

式中参数描述见表3.

表3 起落架横向刚度模型参数Table 3 Parameters of the landing gear lateral stiffness model
2.4 机轮动力学
主轮刹车的受力分析如图3所示,可以看出在飞机滑行过程中,主轮受到刹车力矩Ms和地面摩擦力矩Mj的共同作用.由于考虑了起落架横向刚度的影响,所以就存在一个沿机体纵向的轮轴速度Vzx,它是由飞机速度V和轮轴处起落架变形引起的航向振动速度dV叠加而成的.主轮的动力学方程为
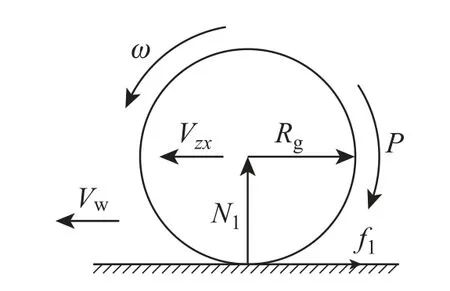
图3 主轮受力图Fig.3 Force diagram of main wheel
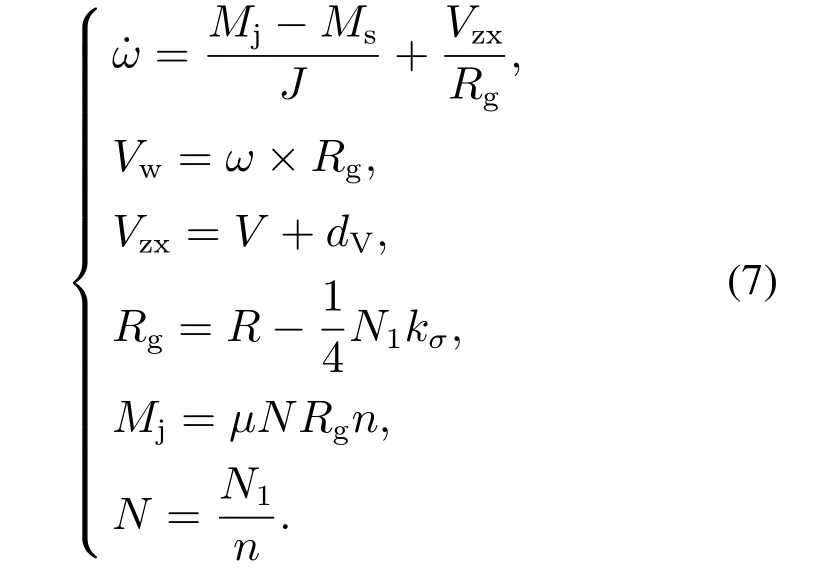
式中参数描述见表4.

表4 主轮参数Table 4 Parameters of the main wheel
在刹车过程中,轮胎受到刹车力矩作用,使得飞机速度始终大于机轮速度,即V >Vw.由此定义滑移率λ,表示机轮相对跑道的滑动运动比率.由文献[36]可知,对于受刹主轮来说,利用轮轴速度Vzx代替飞机速度V来计算滑移率,可避免因起落架变形引起的误松刹,从而有效地改善起落架走步现象.因此本文采用下式计算滑移率:
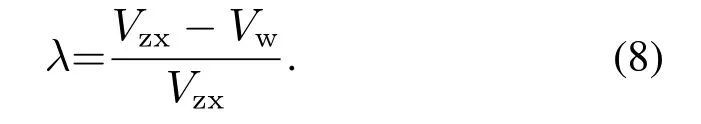
轮胎-跑道结合系数μ和许多因素相关,包括实时跑道状态、飞机速度V、滑移率λ等.由Pacejka[37]开发的一种简单的经验公式-“魔术公式”被广泛应用于计算结合系数,表示为

式中:τj(j=1,2,3),τ1,τ2,τ3分别为峰值因子、刚度因子和曲线形状因子,表5列出几种不同跑道状态下的具体参数.
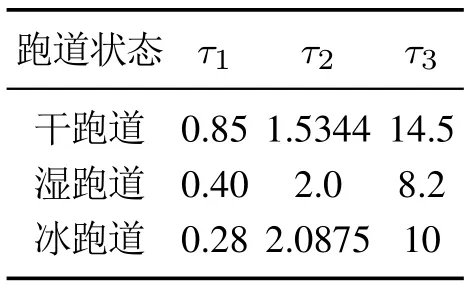
表5 跑道状态参数Table 5 Parameters of the runway status
2.5 液压伺服系统与刹车装置建模
由于液压伺服系统结构复杂,本文对其进行简化,只考虑电液伺服阀和管道,它们的传递函数表示如下:
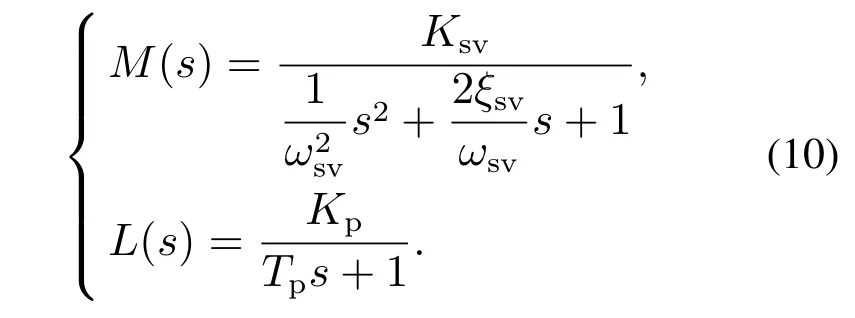
式中参数描述见表6.

表6 液压伺服系统参数Table 6 Parameters of the hydraulic servo system
值得注意的是,防滑刹车控制器应该同时实现刹车控制和防滑控制,因此控制器期望执行器输出的刹车压力P和控制电流Ic之间应存在如下近似的线性关系:
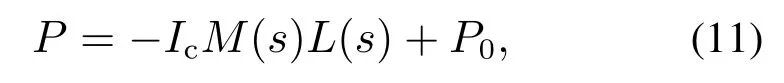
式中P0=1×107Pa.
刹车装置的作用是将刹车压力转化为刹车力矩,其计算方法如下:
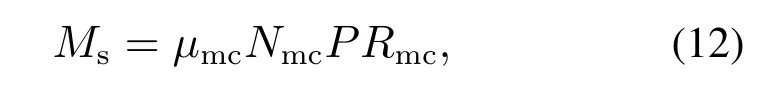
式中参数描述见表6.
液压伺服系统作为AABS的执行器,不可避免地受到一些潜在故障的影响,诸如液压油混入空气、内部渗漏以及振动等问题严重影响了液压伺服系统的工作效率[14].因此,在本文中引入了效率损失(loss of effectiveness,LOE)来代表刹车系统执行器故障,其特点是执行器增益从额定值下降[28].在AABS执行器发生LOE故障的情况下,液压伺服系统产生的刹车压力偏离了控制器所期望的指令输出,即
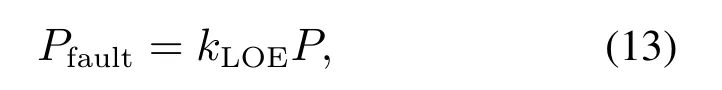
式中:Pfault表示执行器真实输出压力,kLOE∈(0,1]表示LOE 故障因子.
注1n%LOE等 同kLOE=1-,kLOE=1表示执行器无故障.
注2需要注意的是,如果组件并不总是具有与无故障相同的特性,就有必要建立故障模型.这不仅为下一步的重构控制器设计提供了精确的模型,而且还确保了故障-扰动引起的不利影响能够被有效地观测和补偿.
因此,式(12)改写成如下形式:
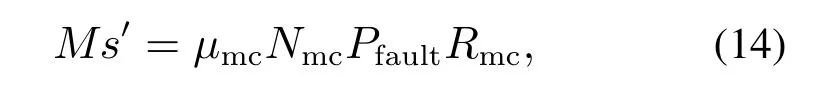
式中是真实刹车力矩.
从上述整个建模过程可以看出,AABS非线性和耦合性很强,执行器故障发生后导致模型参数发生大跳变,相对于无故障系统来说,其内部扰动更大.同时,跑道环境等外部干扰同样不可忽视.
3 重构控制器设计
3.1 问题描述
尽管机体有3个自由度,但AABS只关注纵向滑跑.根据第2节,AABS纵向动力学模型可改写为下式:
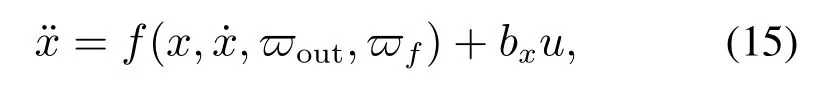
式中:f(·)为被控对象动态,表示外部扰动,为包括AABS所受组件故障在内的不确定项,bx为控制增益,u为系统输入.
本文中AABS采用滑移速度控制类型[1],以飞机速度V作为参考输入,通过控制机轮速度Vω实现防滑刹车.因此系统(15)可以改写为

式中σ1,σ2均为正数.
针对受总扰动影响的系统(17),设计自抗扰重构控制器来抑制或消除故障带来的不利影响,进而实现闭环系统渐近稳定和可接受的工作性能.
3.2 ALADRC重构控制器
建立如下形式LESO:

进一步采用文献[31]中的极点配置法,将系统配置为重根形式,可得
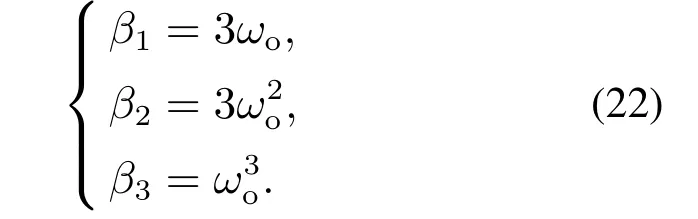
式中:ωo为观测器带宽,ωo越大,LESO观测误差越小,LADRC的控制精度越高,但是会提高系统对噪声的敏感度,因此ωo的选择需综合考虑.
类似地,根据参数化方法及工程经验[33]可选取式LSEF参数为
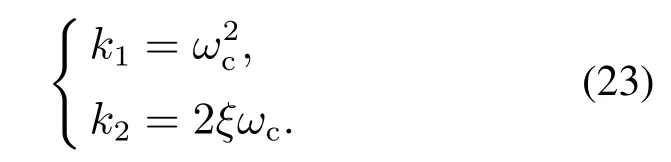
式中:ωc为控制器带宽,ξ为阻尼比,本文取ξ=1.由此LADRC控制器参数整定问题简化为观测器带宽ωo和控制器带宽ωc的配置.
考虑到参数固定的控制器缺乏适应性、控制性能差、鲁棒性弱,在组件出现故障时可能无法使受损系统保持可接受的(额定或降级)性能[39].因此,本节结合了智能控制思想,对传统LADRC方法进行改进,提出了一种基于ALADRC的重构控制器,其实际控制原理图如图4所示.该控制器使用了自适应线性状态观测器(adaptive linear extended state observer,ALESO)和自适应线性状态误差反馈律(adaptive linear state error feedback,ALSEF),二者都是基于BP神经网络,利用状态误差反馈和系统输出信息,实时自动优化观测器和控制器参数.这不仅在带宽法基础上更进一步,消除了手动调参的繁琐,而且使控制器具有重构能力,能够更精确地观测与补偿总扰动带来的不利影响,极大地提升了控制器在面对故障时的适应性和鲁棒性.
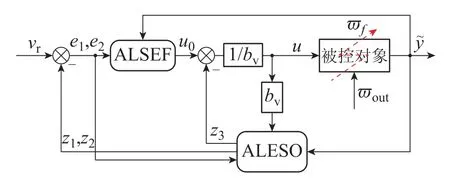
图4 自适应线性自抗扰控制原理图Fig.4 Schematic diagram of ALADRC
下面介绍ALESO结构及算法原理.ALESO内部结构如图5所示,本文采用三层BP神经网络,以状态误差e1、状态微分误差e2、系统输出和1作为神经网络的4个输入节点,观测器带宽ωo作为输出节点,结合AABS模型并经过多次尝试,确定隐含层节点数为5个.
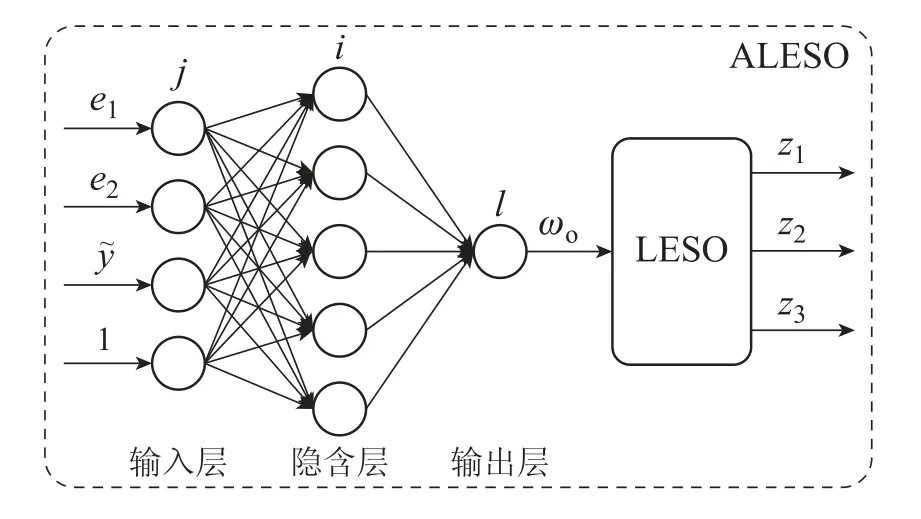
图5 自适应线性扩张状态观测器结构图Fig.5 Structure of ALESO
BP神经网络输入层为

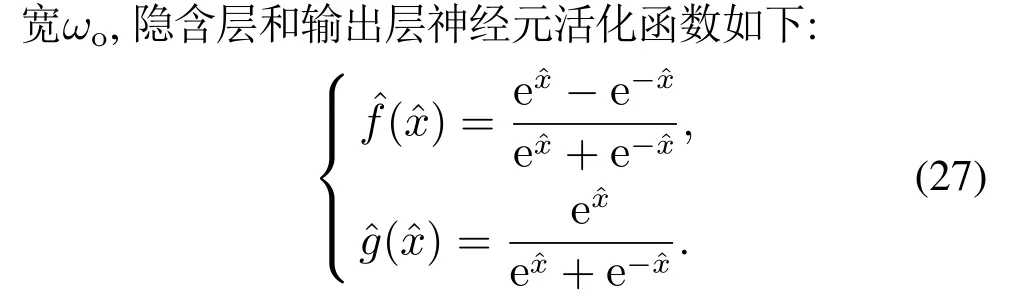
取性能指标函数为
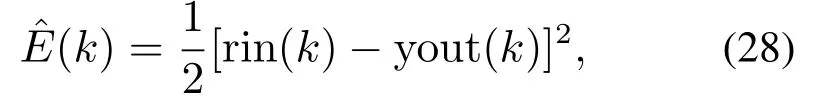
式中:rin=V是系统期望值,yout=Vω是系统输出值.

在给定观测器初始带宽ωo-int后,ALESO可以自动在线更新带宽值来实现状态最优估计.这种方法比传统的手动调节更方便,具有更好的观测性能.同理,ALSEF结构及算法原理与ALESO类似,唯一区别在于控制器带宽ωc作为输出节点,这里不再赘述.
3.3 ALESO估计能力分析
为证明所提出的ALADRC闭环系统稳定性,首先要结合假设1对ALESO的收敛性进行分析[40].
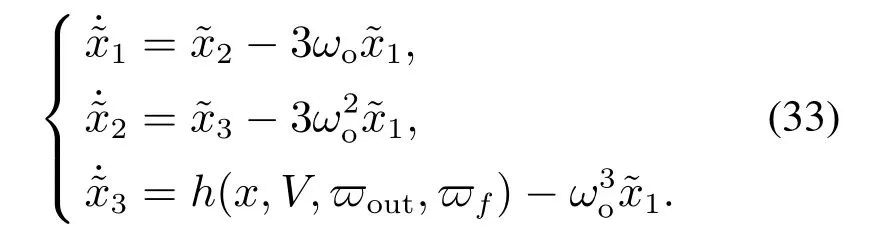

根据假设1和参考文献[41]的定理2,可得如下定理.
定理1在有界的条件下,防滑刹车系统的自适应线性扩张状态观测器的估计误差有界,且其上界随观测器带宽ωo单调递减.
证明见附录.由此可知,存在正数υi,i=1,2,3,使得状态估计误差||≤υi成立,即ALESO估计误差有界,能够有效估计被控对象各状态及总扰动.
3.4 ALADRC的闭环稳定性分析
控制律(19)-(20),被控对象(21)组成的闭环系统为

结合假设1、定理1,以及文献[41]中的定理3和定理4,对闭环系统稳定性进行分析,提出如下定理.
定理2当自适应扩张状态观测器估计偏差有界时,存在控制器带宽ωc,使得闭环跟踪误差有界,对于有界输入,系统输出有界,即闭环系统是有界输入有界输出(bounded input and bounded output,BIBO)稳定的.
证明见附录.因此存在正数υ′,使得闭环跟踪误差|ε(t)|≤υ′成立,即闭环跟踪误差有界,从而闭环系统BIBO稳定.
综上,本文提出的ALADRC利用BP神经网络,根据状态误差和系统输出信息,在线实时动态优化观测器带宽和控制器带宽,在保证闭环系统BIBO稳定的前提下,提高了控制器对总扰动的观测补偿精度,进而增强整个闭环系统的容错能力.该方法赋予了传统鲁棒控制LADRC基于数据驱动的自适应能力,算法简单有效,具有工程应用前景.
4 仿真验证
为了验证所提出方法的重构能力和抗干扰性,本节进行了仿真验证,并与传统PID+PBM以及LADRC进行对比分析.开始时间设置为0,仿真强制结束时间设为50 s,仿真步长采取定步长,步长设为0.001 s,仿真算法为四阶Gunge-Kutta方法.飞机着陆初始速度V(0)=72 m/s,重心初始高度为Hh=2.178 m,俯仰角初始值θ0=0.02 rad,=0 rad/s,刹车装置在1.5 s开始起作用.当飞机速度小于2 m/s,认定防滑刹车控制结束.ALADRC参数如表7所示.
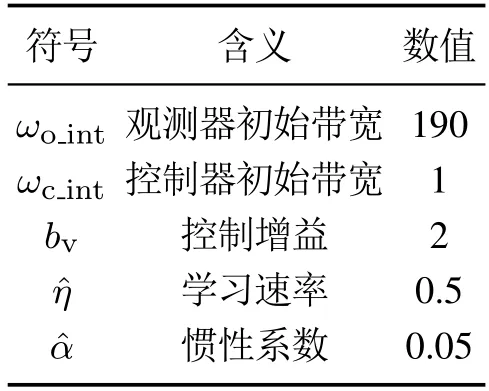
表7 自适应线性自抗扰控制器参数Table 7 Parameters of ALADRC
本文主要选取刹车时间与刹车距离作为刹车效率的依据,通过滑移率变化情况观察系统稳定性.
4.1 干跑道状态下无故障仿真分析
干跑道正常情况下的仿真曲线如图6所示,将3种控制方法在性能方面进行比较,结果如表8所示.可以看出,与传统的PID+PBM相比,LADRC和ALADRC有效缩短了飞机的刹车时间和刹车距离.从图6(c)看出,在刹车初始阶段,PID+PBM有短暂的打滑现象,而LADRC和ALADRC的车轮滑移率平稳.从图6(f)-6(g)可以看出,ALADRC通过在线自动调整参数,实现参数自适应,进而提高了刹车系统性能.从图6(e)可以看出,ALADRC可以精确地观测刹车过程中系统所受扰动.总的来看,ALADRC赋予了观测器和控制器自适应能力,有效地提高了估计和补偿精度,刹车性能明显优于LADRC.

表8 干跑道下无故障AABS性能指标Table 8 Fault-free AABS performance index under dry runway
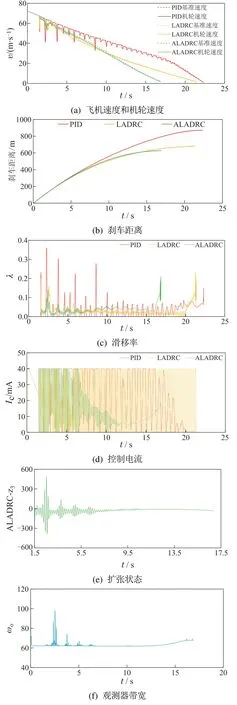
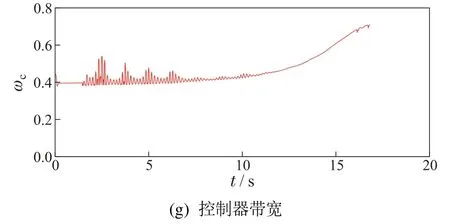
图6 干跑道下无故障仿真结果Fig.6 Fault-free simulation results under dry runway
4.2 干跑道状态下故障–扰动仿真分析
在干跑道状态下进行执行器故障仿真研究:0 s<t≤5 s,无故障;5 s<t≤10 s,执行器LOE 20%;t>10 s,执行器LOE 50%.同时加入一个采样频率为0.001 s,平均幅值为0.07的白噪声作为测量噪声.仿真结果如图7所示,将3种控制方法在性能方面进行比较,结果如表9所示.

表9 干跑道下故障-扰动AABS性能指标Table 9 Fault-perturbed AABS performance index under dry runway
结合图7(a)(c)可以看出,在传统的PID+PBM控制下,连续执行刹车和松刹的操作,导致刹车效率降低,甚至可能造成爆胎,严重威胁了飞机安全.LADRC在前期跟踪效果较好,但在10 s发生了更严重的执行器失效故障后,控制电流不断升高,刹车系统失效,出现了飞机无法刹停的现象.显然,传统PID+PBM 与具有固定参数的LADRC都无法应对严重的组件故障.从图7(e)-(g)可以看出,本文提出的ALADRC面对故障及测量噪声构成的总扰动时,能够迅速在线优化参数,实现控制器重构,提高控制器的抗扰性及鲁棒性,进而更加精确地观测并补偿总扰动带来的不利影响.并且飞机速度和机轮速度自始至终减速平稳,机轮没有出现大幅度打滑现象,刹车效果令人满意.
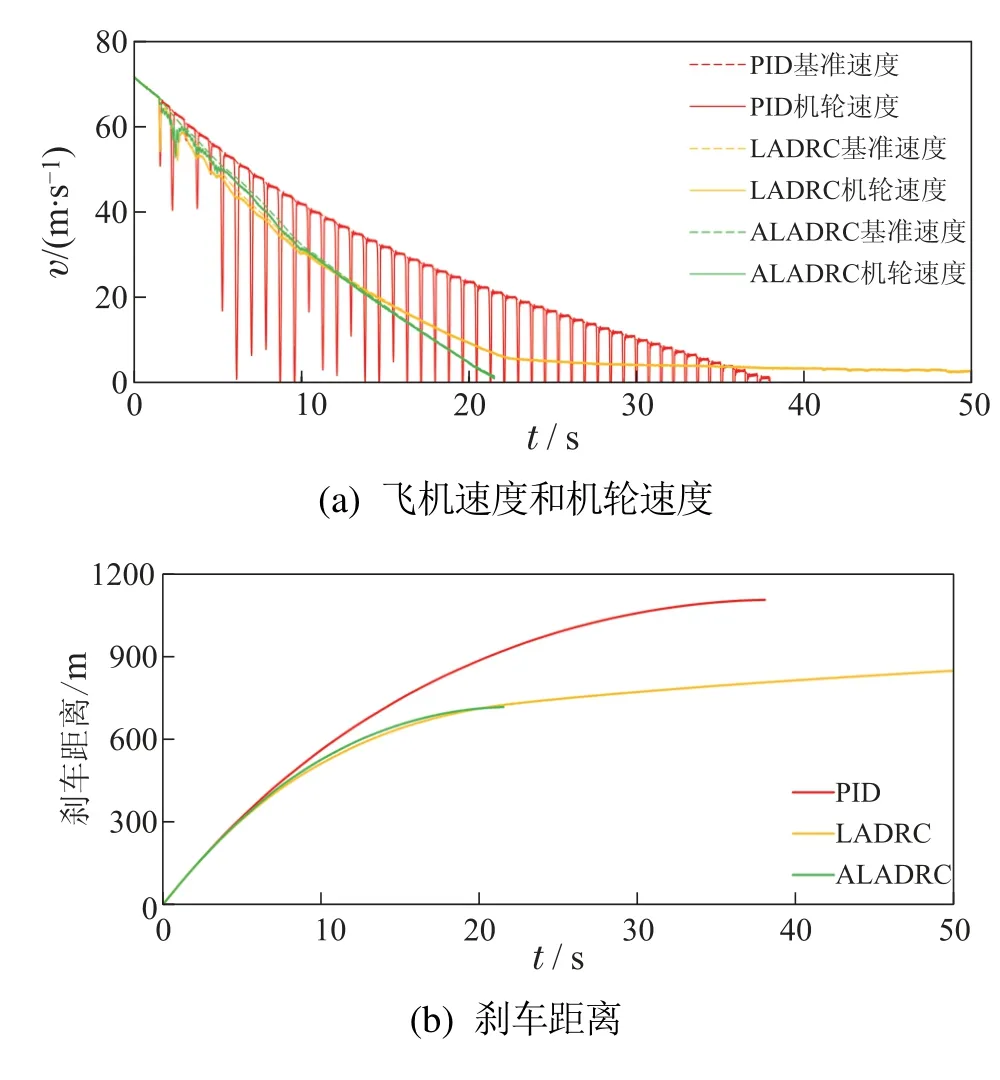

图7 干跑道下故障-扰动仿真结果Fig.7 Fault-perturbed simulation results under dry runway
4.3 混合跑道状态下故障–扰动仿真分析
为验证所提出的ALADRC重构控制器在面对混合跑道时的刹车效果,本节在混合跑道状态下进行组件故障仿真研究:0 s<t≤5 s,干跑道;5 s<t≤10 s,湿跑道;t>10 s,冰跑道.t>5 s时,执行器LOE 50%.同时加入一个采样频率为0.001 s,平均幅值为0.07的白噪声作为测量噪声.仿真结果如图8所示,将3种控制方法在性能方面进行比较,结果如表10所示.从图8(a)可以看出,PID+PBM以及LADRC在50 s内未能使飞机刹停,这在实际应用中是不被允许的.图8(e)-(g)显示,ALADRC仍能实现参数自适应,并且ALESO仍可以精确观测总扰动,整个重构控制系统可以良好地适应跑道变化.总体来说,ALADRC显著提高了故障-扰动下AABS的安全性和可靠性.
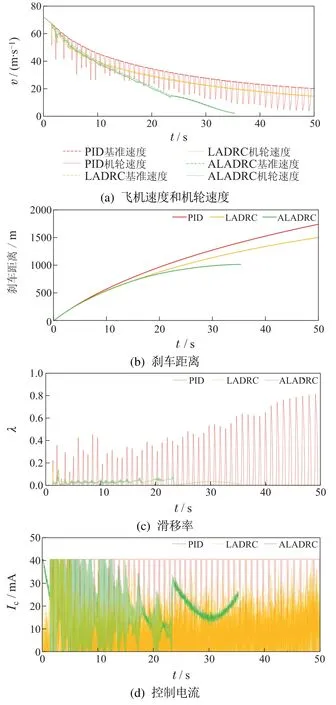
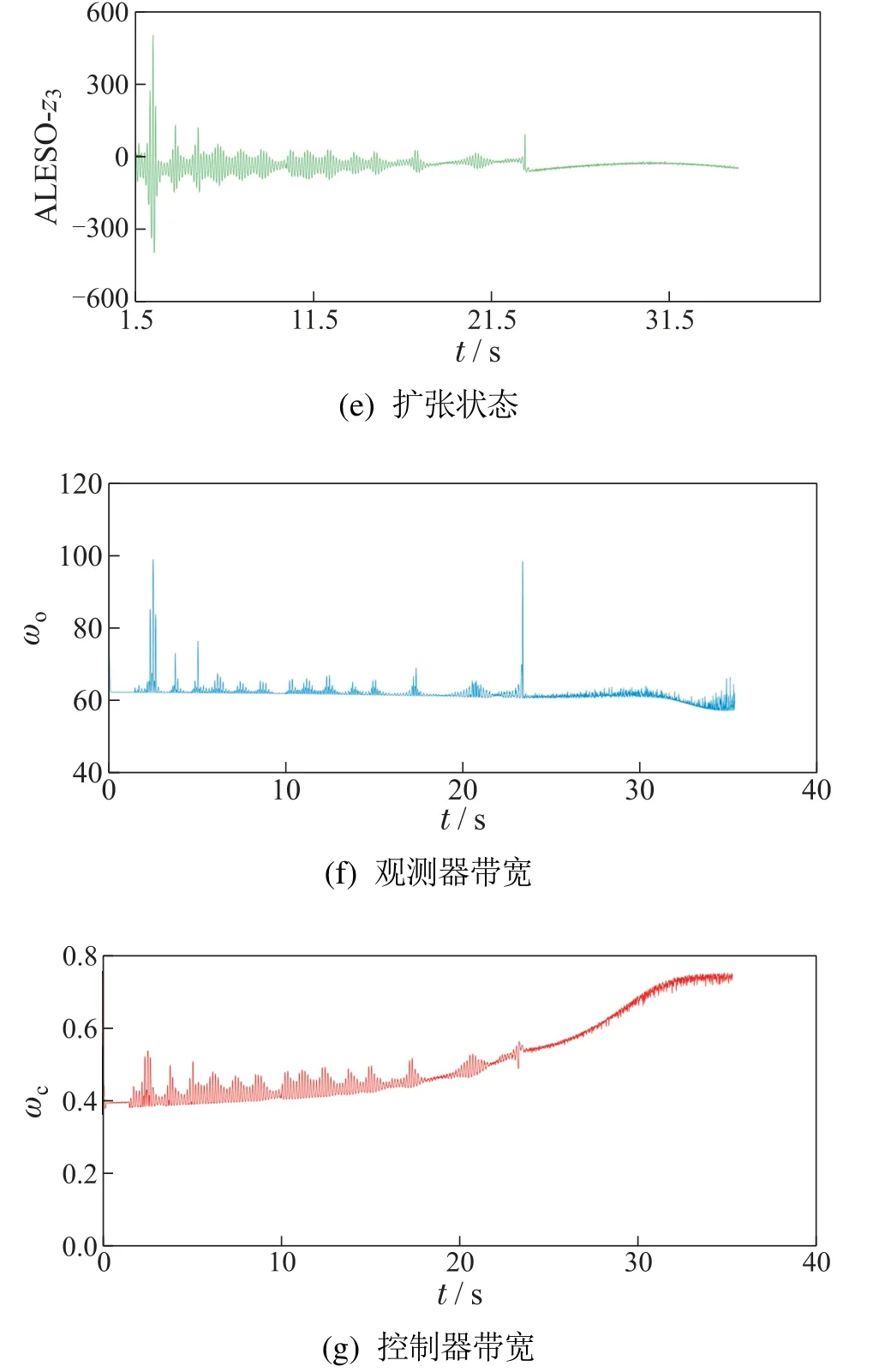
图8 混合跑道下故障-扰动仿真结果Fig.8 Fault-pertured simulation results under mixed runway

表10 混合跑道下故障-扰动AABS性能指标Table 10 Fault-perturbed AABS performance index under mixed runway
5 结论
针对飞机防滑刹车系统易受执行器故障和外部扰动影响的问题,本文研究了一种基于自适应线性自抗扰控制的重构控制方法.根据飞机防滑刹车系统的组成结构和工作原理,建立其数学模型.提出了一种新型的自适应线性自抗扰重构控制器,利用BP神经网络在线调整LESO和LSEF的参数,增强了飞机防滑刹车系统的环境适应性、抗扰性以及鲁棒性.最后,通过在不同跑道环境下的模拟仿真,验证了所提出的重构控制器在故障-扰动状态下能够保持良好的刹车性能,有效地提高了飞机的安全性和可靠性.考虑到微分器对采集信号中的噪声干扰十分敏感,未来工作将尝试引入二阶或高阶跟踪微分器[42]以获得准确的微分信号.此外,半物理仿真实验也同样是未来研究重点.
附录A 定理1的证明
对式(34)进行求解可得
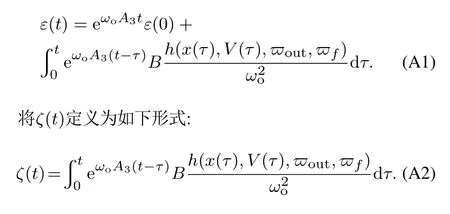

附录B 定理2的证明
根据式(37)和定理1,可得




