非线性时滞系统基于降阶观测器的反步镇定控制

李文杰,张正强

(曲阜师范大学工学院,山东日照 276826)

1 引言

时滞特性和非线性特性在实际系统中普遍存在,譬如,通讯系统、电力系统、网络传输系统等.时滞的存在可使系统的动态性能变差甚至导致系统不稳定[1-2].文献[3]首次将Backstepping方法扩展到非线性时滞系统中且使用Lyapunov-Krasovskii泛函方法设计了无记忆状态反馈控制器.随后文献[4]利用Backstepping方法设计了无记忆状态反馈控制器,研究了一类具有多重时滞的不确定系统的镇定问题.文献[5]通过低增益缩放和Backstepping方法,解决了一类非线性时滞系统的全局自适应输出反馈调节问题.

状态反馈和输出反馈是系统控制设计中两种主要的反馈策略.相对比而言,状态反馈控制的控制率设计有更大的可选择范围,闭环系统能达到更佳性能.文献[6]引入了基于控制增益函数的具有积分型函数的新型Lyapunov-Krasovskii泛函,解决了一类具有时滞和死区输入的非线性系统的状态反馈跟踪控制问题.随后此控制技术被应用于文献[7]中,研究了一类具有互联时滞和多个死区输入的大型系统的模型跟踪控制问题.文献[8]利用一种基于无明确表达形式的控制增益函数的状态反馈控制方法设计了无记忆状态反馈控制器,使得所得到的闭环系统是渐近稳定的.输出反馈所受限制条件较少且不依赖于状态信息,更容易实现.在实际系统中不易获得所有状态信息时,输出反馈控制成为主要控制方法.

本文旨在解决一类具有状态时滞的非线性系统的输出反馈控制问题.通过设计一种新的基于控制增益函数的具有积分型函数的新型Lyapunov-Krasovskii泛函处理时变时滞,并给出控制增益函数的具体表达式.通过Backstepping技术设计无记忆输出反馈控制器,通过仿真结果验证了输出反馈控制的有效性.

为增加文章简洁性,定义如下缩写:

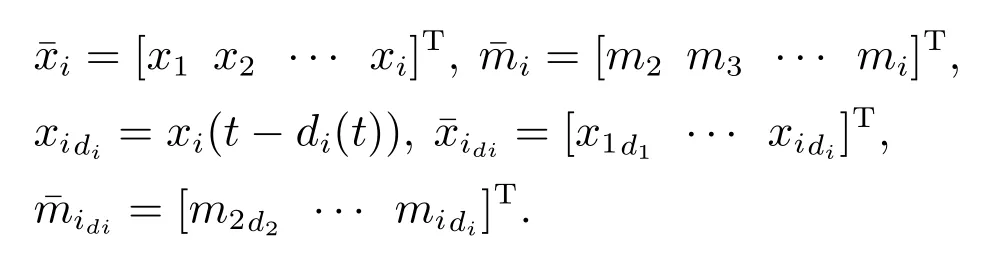
2 问题描述与观测器设计

2.1 问题描述

考虑如下严格反馈非线性时滞系统:

控制目标是设计无记忆输出反馈控制器使得闭环系统的所有信号有界,同时使系统(1)的状态x(t)渐近趋于0.

2.2 观测器设计

由于输出状态x1为唯一的可测状态,可设计降阶观测器以估计不可测状态.首先将系统(1)改写为如下形式:

重新定义观测器的状态以避免上式中输出量y的微分

其导数为如下形式:

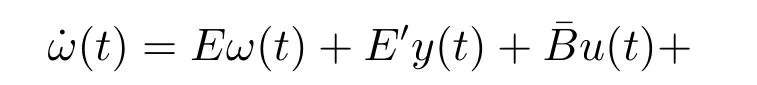
3 控制器设计与稳定性分析

3.1 静态增益函数设计

3.2 控制器设计

对于状态估计误差系统,考虑以下Lyapunov候选泛函:

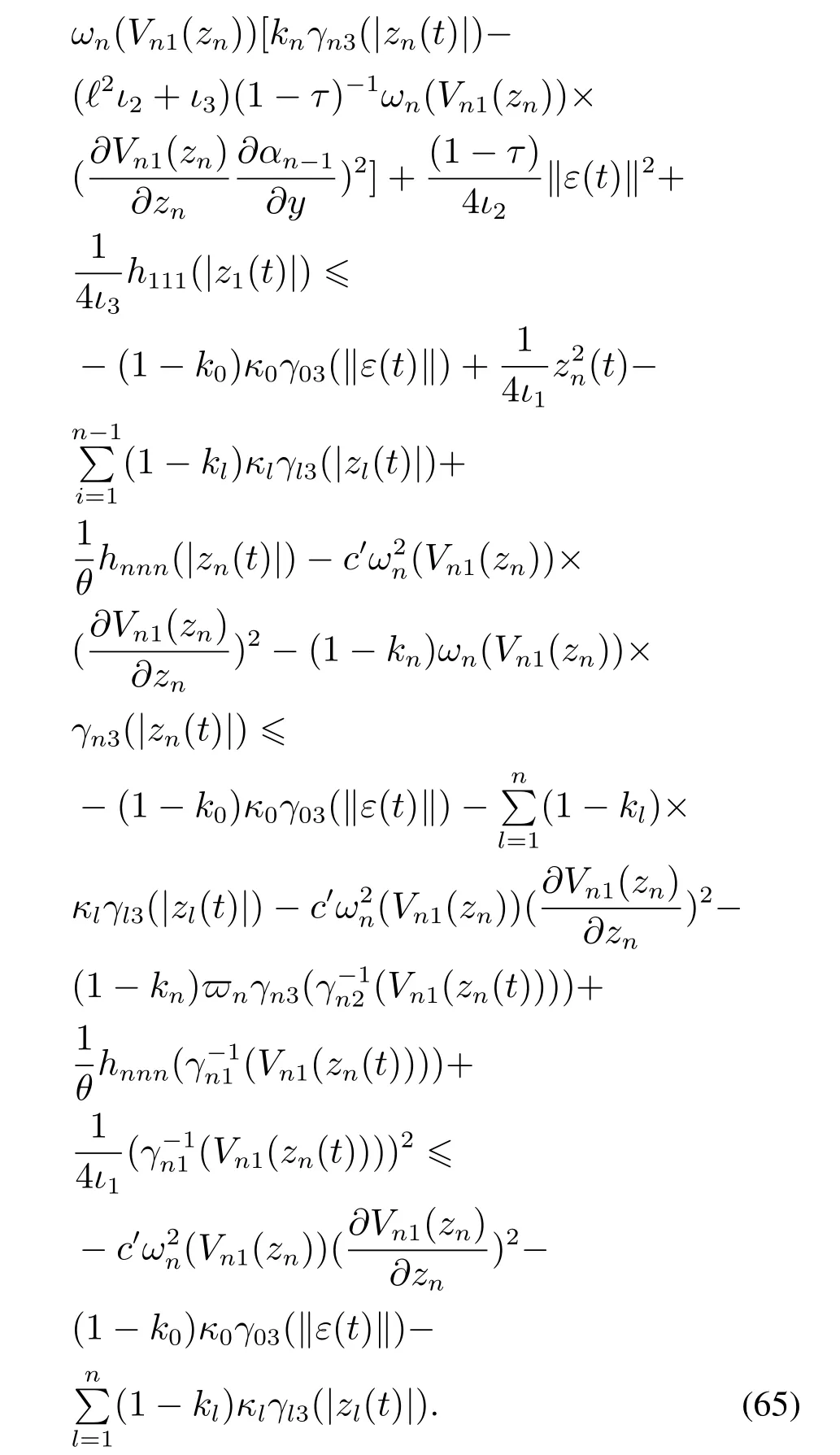
3.3 稳定性分析

定理1由系统(1)、降阶状态观测器(9)、虚拟控制率(14)-(16)、控制器(63)构成的闭环系统在满足假设1-5的条件下,所有闭环信号是有界的并且系统(1)的状态x(t)渐近趋于0.

证对式(65)两端求t0到t定积分,可得

4 仿真

考虑严格反馈非线性时滞系统如下:

其中参数c′=12.初始值定为x1(t)=0.5,x2(t)=-0.5,t ∈[-τ,0],m(0)=0.5.状态响应曲线如图1所示,系统状态x1(t),x2(t)渐近收敛于0,未知状态x2(t)及其估计(t)渐近收敛于0,图1(c)描述了控制输入u(t).仿真结果验证了控制器的有效性.

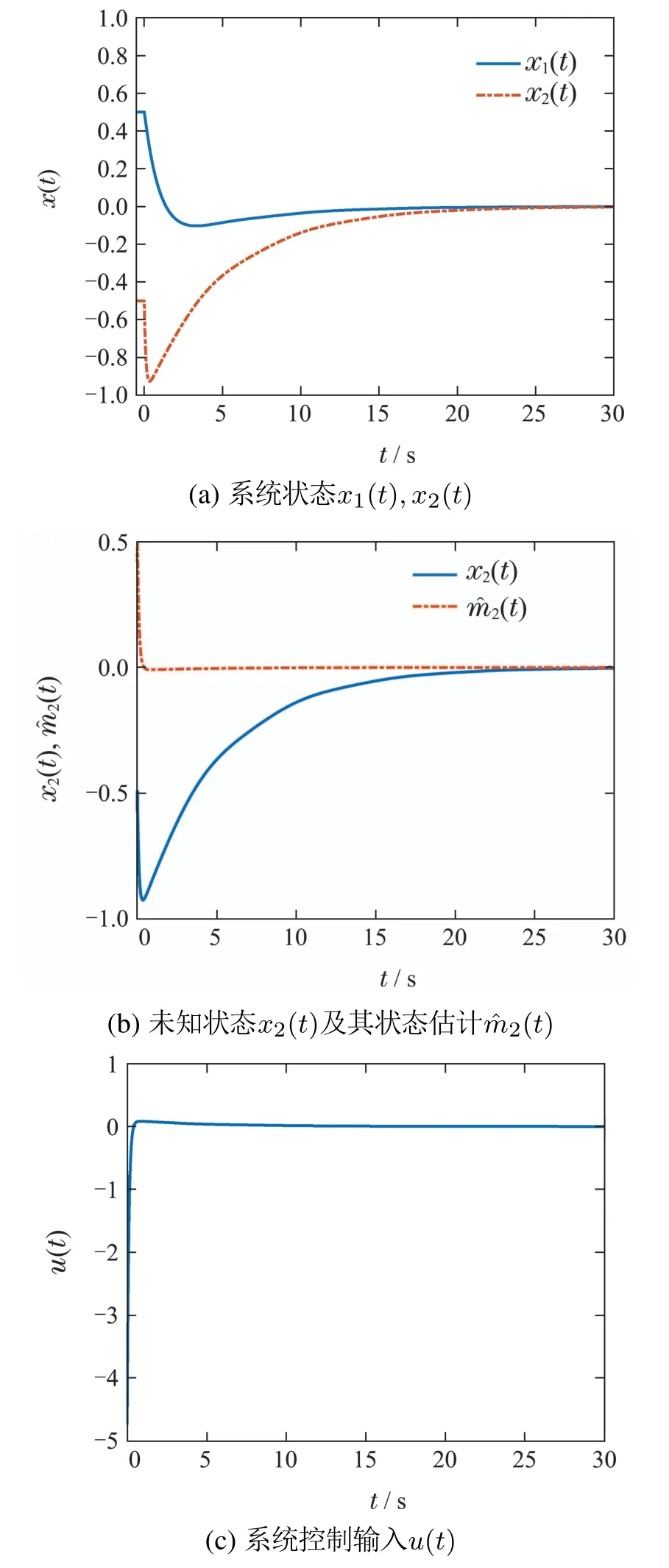
图1 闭环系统响应Fig.1 Closed-loop system response

5 结论

本文研究了一类具有未知时滞的非线性系统的渐近稳定问题.本文采用了降阶观测器估计不可测状态.提出了新的Lyapunov-Krasovskii函数补偿未知时滞函数,设计了控制增益函数处理非匹配项以及Lyapunov-Krasovskii函数补偿时滞时产生的非负项.详细地证明了基于静态增益函数的的输出反馈控制方案可以实现所有闭环信号的有界性以及系统的渐近稳定性.仿真结果验证了此控制方案的有效性.如何放宽假设条件值得进一步研究.