勒让德多项式拟合IGS 精密星历的算法改进

申少飞，雷伟伟，李振南

(河南理工大学 测绘与国土信息工程学院,河南 焦作 454003)

0 引言

在进行GPS 精密单点定位(PPP)时，需要用到卫星的精密在轨位置.目前有两种获取卫星轨道坐标的方法，分别是通过广播星历和事后发布的精密星历获得[1].广播星历是通过瞬时参数求得卫星速度与位置，计算复杂且精度较低，精密星历的卫星位置和钟差精度要高于广播星历求得的卫星位置和钟差精度两个数量级[2].因此，广播星历求得的卫星轨道坐标精度在实际应用中难以满足高精度用户的需求.精密星历由国际GNSS 服务(IGS)提供，是由若干卫星跟踪站的观测数据，经事后处理算得的用于卫星精密定位等使用的卫星轨道信息，其精度可达5 cm 甚至更高.IGS 发布的精密星历采样数据间隔为15 min，而接收机的采样率通常为30 s、15 s甚至更短的时间间隔[3]，因此需采用轨道逼近的算法求取时间间隔更短的卫星轨道坐标.目前用于轨道逼近的方法主要分为插值法和拟合法[4].

常用的插值方法有拉格朗日插值法、牛顿插值法、Neville 插值法和三角插值[5-7].常用的拟合方法包括切比雪夫多项式拟合和勒让德多项式拟合[8].目前最常用的插值方法是拉格朗日插值法，但是当改变插值点的个数时，需要重新计算，且计算量大，为此引入了牛顿插值法和Neville 插值法.文献[9]说明拉格朗日插值法与Neville 插值法实质是一致的，但当阶数增加时，Neville 插值法原有计算仍然可用，插值公式不需要全部建立.文献[10]指出当取合适的阶数时，三种插值方法的插值精度都能达到毫米级.当卫星插值的轨道弧段较长，需要将公式展开到较高的阶次，此时，拉格朗日插值容易在区间两端出现龙格震荡现象.为解决这个问题，文献[11]采用滑动式拉格朗日插值方法对GPS 精密星历进行插值，插值精度较好，即使阶数较高，也不会出现龙格现象.文献[12]采用一种新方法，即三角插值，得到的插值精度和滑动式拉格朗日插值相当.文献[13]采用改进的切比雪夫多项式拟合法，在进行高阶次的轨道拟合时，也能保持较高的精度和稳定性.文献[14]采用勒让德多项式拟合法，并与拉格朗日插值法进行比较，结果表明勒让德多项式拟合能达到毫米级精度且不会出现龙格震荡之类的现象.文献[15]指出用拟合法在计算系数时需要对法方程进行求逆，阶数过高容易使矩阵出现奇异，使法方程变为病态方程，系数的微小变动都会对解产生较大的误差.

常规的勒让德多项式方法在高阶求逆时会产生较大的误差，稳定性差.对此，本文使用改进的勒让德多项式拟合法求解，采用LU 分解(LU Decomposition)算法和奇异值分解(SVD)算法求解轨道拟合，与常规算法相比具有更高的精度和稳定性.

1 改进的勒让德多项式拟合法数学模型

1.1 勒让德多项式拟合法

设拟合区间的初始历元为t0，拟合长度为 Δt.在时间段 [t0,t0+Δt] 内，以n阶勒让德多项式为基函数拟合卫星轨道坐标时，使用转换公式[14]

将变量t归化到区间 τ∈[-1,1]，卫星轨道坐标的勒让德多项式拟合函数为

式中：n为勒让德多项式的阶数；分别为卫星轨道X、Y、Z坐标分量的多项式系数.其中，Pi递推公式为[16-17]

1.2 常规算法求解多项式系数

以式(2)中GPS 卫星坐标X分量中的系数为例，由式(2)～(3)可求得GPS 卫星拟合坐标.设IGS提供的GPS 卫星X坐标分量的精密星历为Xi，则观测值向量的误差方程为[14]

将式(4)简化为矩阵形式

式中：m为计算过程中用到的IGS 精密星历的个数；X(τi)为对应历元时刻的精密星历.

根据最小二乘原理VTPV=min 可得

直接求逆，解得多项式系数矩阵C为

各历元坐标可视为是等权观测值，所以P为单位矩阵，则求解多项式系数矩阵C可以写为

将式(7)中求得的多项式系数矩阵代入式(2)中，即可求得GPS 卫星轨道在X方向坐标的拟合多项式.同理可求得GPS 卫星在Y方向和Z方向的坐标拟合多项式.

1.3 LU 分解法求解多项式系数

根据普通最小二乘原理得到法方程式(6)，P为单位矩阵，可化简为

设A=BTB，式(9)可写为

用高斯消去法对式(10)求解，可用矩阵表示为[18]

式(11)中，把方阵A分解为一个下三角矩阵和一个上三角矩阵，称为 LU分解.P为初等变换矩阵.

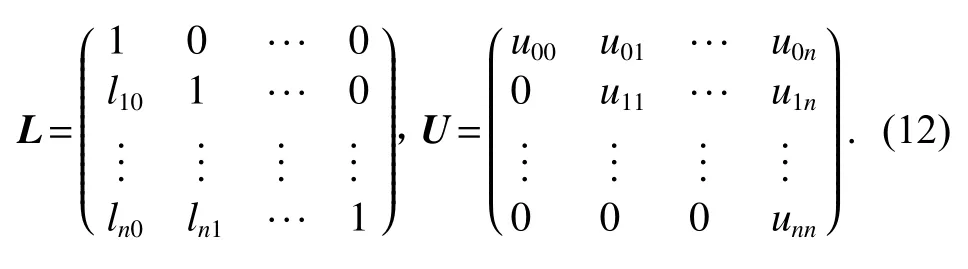
则方程(10)可以改写为

令b=BTX，则

令UC=Y，则有LY=b.那么由此把原方程的求解变为求解系数矩阵为三角阵的方程，很容易实现.以上过程即，首先计算A的 LU分解，由LY=b可得Y，接着由UC=Y求得多项式系数向量C.

1.4 SVD 分解法求解多项式系数

通过以矩阵SVD 分解为基础的Moore-Penrose伪逆矩阵法求解GPS 卫星轨道坐标拟合函数系数C，系数C为

式中，B+为矩阵B的Moore-Penrose 伪逆矩阵，其Moore-Penrose 伪逆矩阵求解方法如下.

1.4.1 对矩阵B进行SVD 分解[18]

式中：

U为(m)×(m)维正交矩阵，V为(n+1)×(n+1)维正交矩阵，ui和vi为各自矩阵内部两两正交的单位向量，S为(m)×(n+1)维对角矩阵，Si为矩阵的奇异值(并且S0≥S1≥···≥Sn≥0)，以上三个矩阵的维数是通过矩阵B的维数所确定的.

1.4.2B的Moore-Penrose 伪逆矩阵

式(17)中的S+为矩阵S的伪逆矩阵，是矩阵S的非零元素取倒数之后再转置得到的，所以S+为(n+1)×(m)的矩阵，其形式为

至此根据式(15)和(17)即可求得GPS 卫星轨道坐标拟合函数系数C.将求得的系数C代入式(2)中，可求得任意时刻的卫星坐标.

2 勒让德多项式拟合改进算法分析

本文从IGS 官网下载2019 年9 月29 日的卫星精密星历作为计算数据，历元时刻为00:00:00—23:45:00.采样间隔为15 min，以拟合时段3 h 为例，采样点所对应时刻为0 min、15 min、30 min、45 min、···、180 min.为了验证拟合精度，选取采样点相同时刻的拟合点，运用多项式求出轨道坐标拟合结果，并与拟合点处历元所对应的卫星坐标进行作差比较，求出误差绝对值的最大值和误差中误差，并求出每种拟合方法的点位中误差.

选取3 h、6 h、12 h 三个拟合时段进行拟合分析，采样初始时刻为00:00:00，对3 种算法的拟合结果进行对比分析，运算环境在MATLAB 9.8 下进行.IGS 精密星历提供的坐标误差一般小于5 cm，因此3 种算法的拟合精度至少要小于5 cm.表1、表2 中差值是指拟合结果与对应历元卫星坐标X方向差的绝对值的最大值；均方根(RMS)是卫星坐标X分量拟合结果的中误差；点位中误差是卫星坐标X、Y、Z方向中误差和的平方根.

2.1 拟合时段为3 h 的勒让德多项式拟合精度分析

表1 给出勒让德多项式拟合时段为3 h 的X方向拟合误差绝对值的最大值和中误差，可以看出3 种拟合方法无论是误差绝对值的最大值还是中误差结果一致，都随着阶数的增大而减小.在第8 阶时，3 种拟合方法误差绝对值的最大值均为69.01 mm，中误差均为44.52 mm.在第9 阶时，误差绝对值的最大值和中误差精度都迅速提高，达到了毫米级.随着阶数的增大，在11 阶时误差绝对值的最大值和中误差达到最小，分别为0.08 mm 和0.04 mm.拟合时段为3 h的Y方向勒让德多项式拟合误差绝对值的最大值与中误差和Z方向勒让德多项式拟合误差绝对值的最大值与中误差，与X方向的规律大致一样.图1 给出了3 种拟合方法的点位中误差变化曲线，和表1 一样，3 种拟合方法的精度变化完全一样，都随着拟合阶数的增大而不断提高.这说明在拟合时段较小，阶数较低时，3 种拟合方法的精度完全一样.

表1 X 方向勒让德多项式拟合(拟合时段3 h) mm

图1 点位中误差变化曲线(拟合时段3 h)

2.2 拟合时段为6 h 的勒让德多项式拟合精度分析

由表2 可知，在拟合时段为6 h 的勒让德多项式拟合中，采用常规算法的误差绝对值的最大值与中误差随着阶数的不断升高呈现先减小后增大的趋势.在10～21 阶时，误差绝对值的最大值与中误差不断减小，在第10 阶时分别为402.82 mm 和205.97 mm，误差精度较低.随着阶数的升高，在第21 阶时精度达到最高，分别为0.27 mm 和0.15 mm，精度达到亚毫米级.接着随着阶数的升高精度不断降低，在23 阶时，常规算法的误差绝对值的最大值和中误差分别为319.34 mm 和102.68 mm，精度达到了分米级，达不到卫星轨道坐标的精度要求.LU 分解法和SVD 分解法的误差绝对值的最大值与中误差则随着阶数的升高不断减小，且精度几乎一致，在第10 阶时，分别为402.82 mm 和205.97 mm.随着阶数的不断增大，两种算法的精度不断提高，在第23 阶时精度达到了最高，LU 分解法误差绝对值的最大值与中误差分别为0.21 mm 和0.08 mm，SVD 分解法误差绝对值的最大值与中误差分别为0.20 mm 和0.08 mm，精度均较高.可以看出在拟合阶数较高时，LU 分解法与SVD分解法明显比常规算法精度高.拟合时段为6 h 的Y方向勒让德多项式拟合误差绝对值的最大值与中误差和Z方向勒让德多项式拟合误差绝对值的最大值与中误差，与X方向的规律大致一样.图2 给出了3 种拟合方法的点位中误差变化曲线，其结果和表2中3 种方法的规律相似，也进一步验证了LU 分解法与SVD 分解法在高阶时比常规算法更有优势.

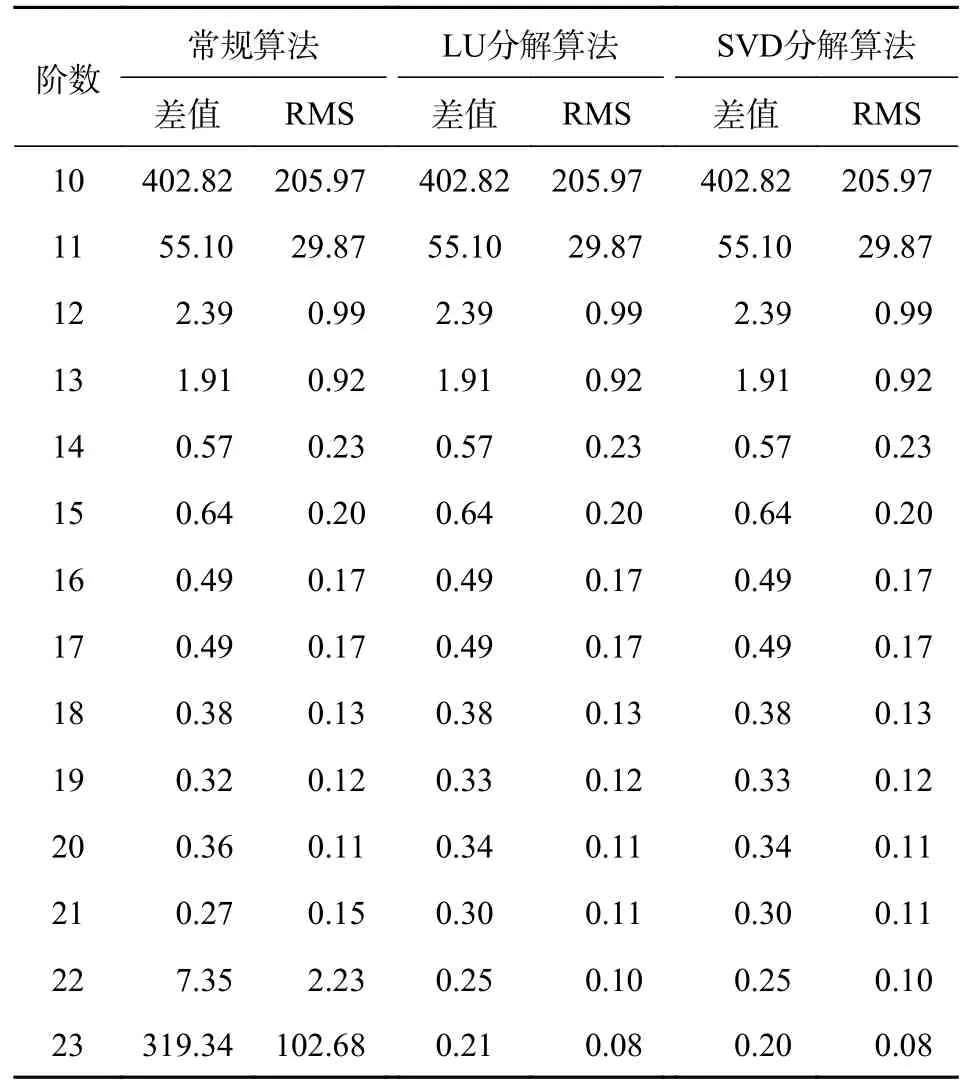
表2 X 方向勒让德多项式拟合(拟合时段6 h) mm

图2 点位中误差变化曲线(拟合时段6 h)

2.3 拟合时段为12 h 的勒让德多项式拟合精度分析

由图3～4 可知，当拟合时段为12 h，拟合阶数较低时，3 种拟合方法在X方向误差绝对值最大值和中误差变化曲线一致，随着阶数的增大而不断减小，趋近于0.从34 阶开始，常规算法误差绝对值的最大值和中误差则随着拟合阶数的增大精度不断降低，LU分解法和SVD 分解法的变化曲线则继续趋近于0.从42 阶开始，LU 分解法的精度开始降低，曲线趋于发散.而SVD 分解法不会出现类似的情况，随着阶数的增大，误差绝对值的最大值和中误差不断减小，拟合精度越来越高，在拟合的最大阶数处，精度最高，拟合曲线趋于收敛.图5 是拟合时段为12 h 的点位中误差，拟合曲线变化趋势和图3～4 大致一样.从3 张图中可以看出，拟合精度最高最稳定的是SVD 分解法.

图3 X 方向误差最大值变化曲线(拟合时段12 h)

图4 X 方向中误差变化曲线(拟合时段12 h)

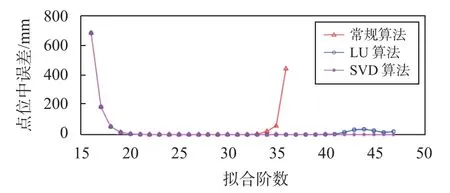
图5 点位中误差变化曲线(拟合时段12 h)

2.4 从条件数角度对结果进行分析

在拟合时段为3 h、6 h 和12 h 时，3 种拟合方法的拟合精度并不完全一样.在拟合时段为3 h 时，3 种拟合方法的精度完全一致.在拟合时段为6 h 时，常规算法的误差在阶数较高时开始增大，而另外两种拟合方法则能保持较高的精度.在拟合阶数较高，即拟合时段为12 h 时，LU 分解法的精度在高阶时也开始降低，SVD 分解法无论低阶还是高阶都能保持较高的精度.这是因为在拟合时段较短，即3 h 时，法方程系数矩阵BTB维数较低，不易成为奇异矩阵，因此用常规算法对BTB求逆时，精度较高，与LU 分解法和SVD 分解法的精度相当.当拟合时段为6 h 时，法方程系数矩阵BTB维数超过了20，此时矩阵很容易成为奇异矩阵，因此再用常规算法进行多项式系数求解时，很容易出现较大的误差.采用LU 分解法和SVD分解法不需要对矩阵求逆，而是分别对BTB和B矩阵进行分解，因此两者精度都远远高于用常规算法求得的系数C的精度.

在拟合时段为12 h 时，此时拟合阶数较高，矩阵B和BTB的维数变得很大，因此在拟合过程中除了要解决满秩矩阵，还要解决病态矩阵的问题.由于在计算病态性矩阵方程的解时误差几乎是不可避免的，所以在可能的时候识别并避免病态性的矩阵是重要的，一般以条件数来衡量矩阵的病态性.由表3 可知，随着阶数的升高，矩阵B和BTB的条件数越来越大.在第40 阶时，BTB的条件数已经达到了1013，按照双精度，我们会得到16-13=3 位正确数字的解C[18].LU 分解法是通过对矩阵BTB进行LU 分解来求得多项式系数C，因此拟合阶数过高，精度就会出现一定程度的下降.而SVD 分解法实则是对矩阵B进行SVD 分解来求得系数C，所以即使在第47 阶时，条件数也只是达到了1011，还能保持较高的精度.因此用SVD 分解法无论是低阶还是高阶都能保持较高的精度.

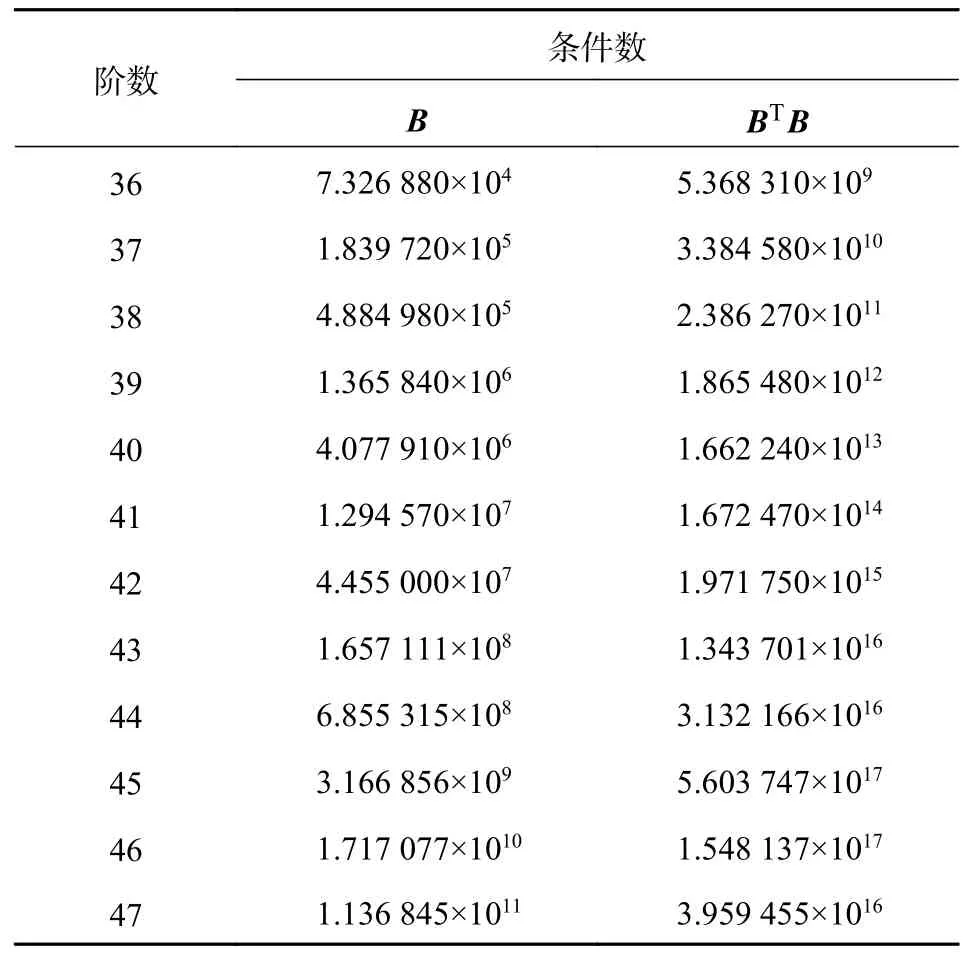
表3 矩阵条件数(拟合时段12 h)

3 结束语

计算表明，3 种勒让德多项式拟合卫星轨道坐标的求解方法在不同拟合时段和拟合阶数精度各不相同.在拟合时段为3 h，即拟合阶数较低时，3 种拟合方法精度相当.在拟合时段为6 h 时，由于拟合阶数较高，常规算法已不能满足卫星轨道坐标的精度，改进的LU 分解法和SVD 分解法对奇异矩阵都有较好的解决方法，因此精度相当.在拟合时段为12 h 时，拟合阶数进一步提高，此时在拟合过程中不仅存在奇异矩阵，还存在病态矩阵的问题.SVD 分解法对两种问题都能较好的解决，所以在高阶拟合时，无论是在精度还是稳定性方面都要优于LU 分解法和常规算法，具有较好的优势.数字拟合精度越高，表明拟合求得的多项式越逼近卫星轨道坐标，则对原星历的精度影响越小.因此以后在采用勒让德多项式对GPS 卫星轨道坐标进行拟合时，可以优先采用SVD 分解法进行轨道坐标拟合.