广义热弹模型的热力学基础与瞬态响应1)
吴 华 邹绍华 徐成辉 尉亚军,†,2) 邓子辰,3)
* (西北工业大学力学与土木建筑学院,复杂系统动力学与控制工信部重点实验室,西安 710129)
† (西安交通大学机械结构强度与振动国家重点实验室,西安 710049)
引言
热传导理论是热弹耦合理论的重要基础,经典傅里叶热传导定律为
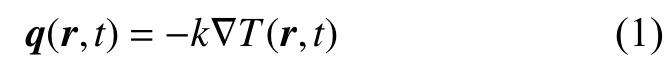
其中,k为热传导系数,q为热流,T为温度.傅里叶定律及其热弹耦合理论被广泛用于描述热力共同作用下材料/结构的热传导和变形行为.同时,傅里叶定律表明[1-3]: 热以无限大速度传导,即一点的温度变化能瞬间传导到无穷远处.解决这一理论“悖论”成为不断推动热传导方程深入发展的动力.同时,飞速发展的激光、集成电路等技术领域,具有作用载体和作用环境极小、作用时间极短的特点,使得器件在极小空间、极短时间内产生大量热量.建立在宏观、近平衡态的经典热传导和热力耦合关系不再适用于此类以微纳尺度和超快热冲击为代表的极端非平衡态问题[4-6].
为此,国内外学者提出了多种广义热传导模型,并建立了相应的广义热弹性理论.Cattaneo[7]和Vernotte[8]提出了CV (Cattaneo-Vernotte)热传导模型
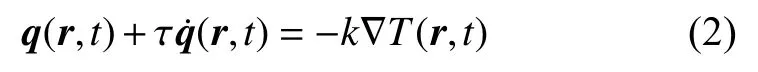
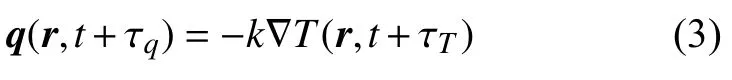
其中,τq,τT分别为热流相、温度梯度相的松弛时间.若左右两端分别按一阶泰勒级数展开,可得到
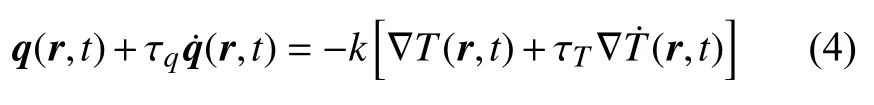
Green 等[10-11]提出了GN (Green-Naghdi)热传导模型
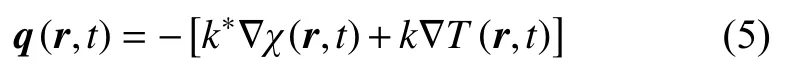
其中,k*为导热比,χ为热位移:χ˙=T.当k*=0 时,该式退化为傅里叶定律.对式(5)求导,可得
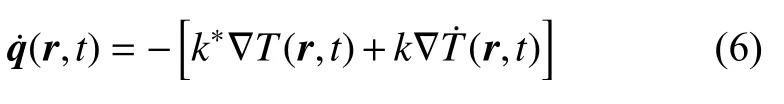
通过量纲分析,引入关系式k*=k/τ,则GN 热传导方程可进一步改写为
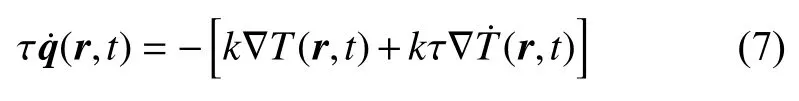
在GN 模型(5)中也考虑热流率和松弛时间,可以得到MGT (Moore-Gibson-Thompson) 热传导方程[12-13]
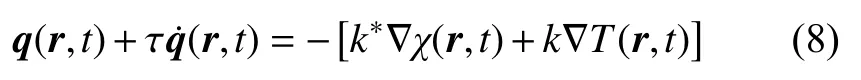
同样地,考虑到关系式k*=k/τ,则有
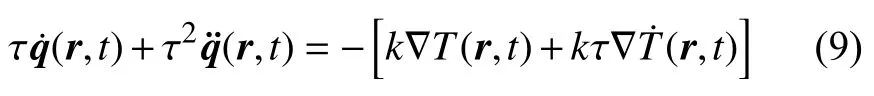
其他的广义热传导模型包括: Cao 等[14]基于相对论理论,并计及声子质量,建立的热质热传导方程;Kuang[15]通过引入惯性熵的概念,建立的惯性熵理论等.
广义热传导的研究直接推动了广义热弹耦合理论的发展.Lord 等[16]在CV 热传导模型的基础上,建立了LS 广义热弹性模型;Bazarra 等[17]在该模型的基础上探讨了材料孔隙率对瞬态响应的影响;Green 等[11]建立了无耗散的GN 热弹性理论;El-Karamany 等[18]考虑了滞后效应,建立了GN 模型Ⅱ型和Ⅲ型的单相滞后、双相滞后模型;Alizadeh Hamidi 等[19]探讨了GN 模型在Euler-Bernoulli 梁的运用;Tzou[20-21]由理论推导建立了DPL 热弹耦合理论,针对瞬态响应和滞后效应开展了大量实验研究;Singh[22]模拟了平面波在横观各向同性双相滞后广义热弹性固体中的传播,以图形方式显示了双相滞后热弹性和LS 广义热弹性情况下的传播角度;Quintanilla[23]发展了MGT 热弹性理论,并考虑了双温下的扩展,证明了解的多项式衰减;Youssef[24]基于热质热传导方程,构建了双温度广义热弹性理论;文献[25-27]建立并发展了GL 热弹耦合理论,讨论了应变率的影响,证明了解的唯一性定理.此外,考虑空间尺度效应和时间记忆效应的热弹耦合理论也已取得较大进展,如分数阶微积分[28-31]和非局部效应[32-33]的引入等.
综上,广义热传导模型的形式多样,对应的热弹耦合理论也很丰富.因此,存在的问题有: (1) 如何从连续介质力学视角,建立起相关理论模型的热力学基础;(2) 各模型之间存在怎样的关联,如何揭示之.
基于拓展热力学原理,本文建立了广义热弹耦合理论的新模型,是现有相关模型的统一形式,可通过参数赋值实现模型的退化.此外,提出了热学“弹性”单元和“黏性”单元,通过串并联模式实现了上述模型的重构,从而揭示了已有模型间的关系.结合数值分析结果,研究了各模型中松弛时间等对瞬态响应结果的影响规律.
1 拓展热力学和广义热弹耦合理论
根据连续介质力学,热力学第一定律为
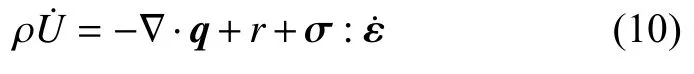
其中,ρ 为密度,U为比内能,r为内热源,σ 为应力张量,ε 为应变张量.热力学第二定律为
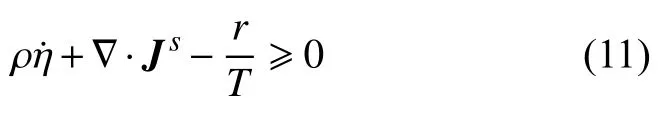
其中,η为比熵,Js为熵流矢量.引入比亥姆霍兹自由能ψ

由式(10)~式(12),有
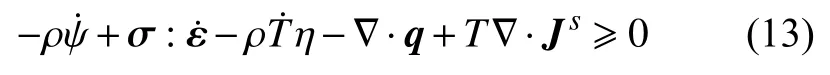
根据拓展热力学,现引入高阶热流[34]
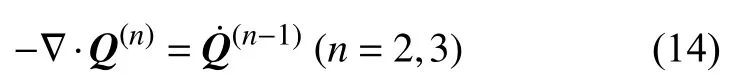
其中一阶热流Q(1)是经典热流q=Q(1).经典热力学中,熵ρη 是比内能和应变的函数.对于拓展热力学,假设其也是各阶热流、温度梯度的函数,则拓展的吉布斯方程为

由式(12)进一步可知,比亥姆霍兹自由能 ψ 是温度、应变、各阶热流和温度梯度的函数,故有
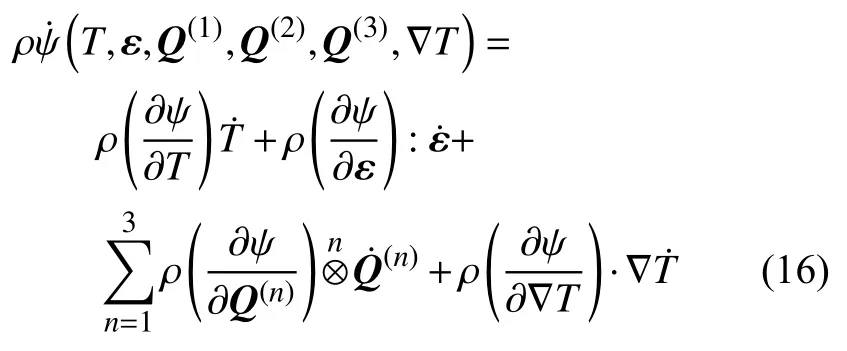
其中
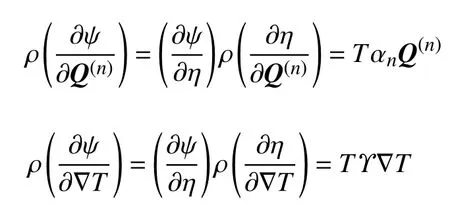
代入式(16),有
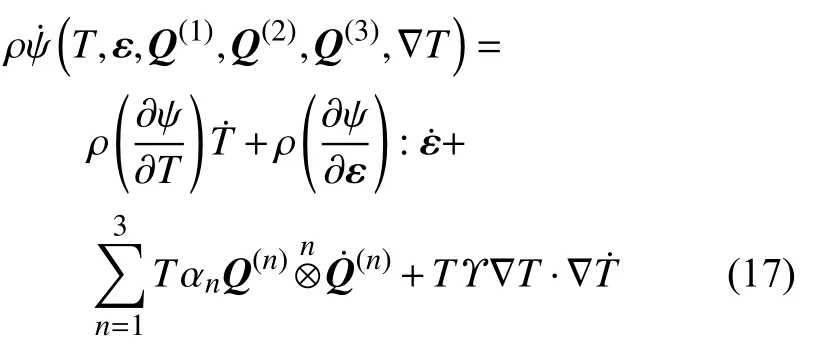
由式(13)和式(17)可得

可得

经典热力学的熵流为Js=T-1q,通过考虑高阶热流项,将其拓展为
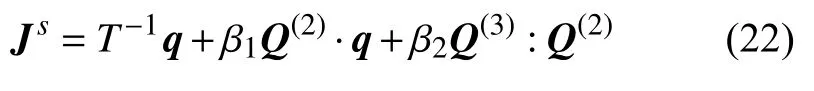
上式代入式(21),并由正定性得
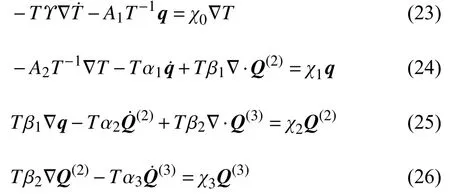
其中,A1和A2满足A1+A2=1 ,χi(i=0,1,2,3)≥0 .考虑式(14),并由式(26)可得
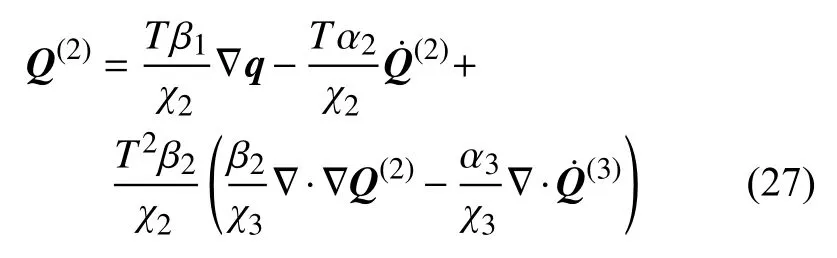
将上式代入式(24),有
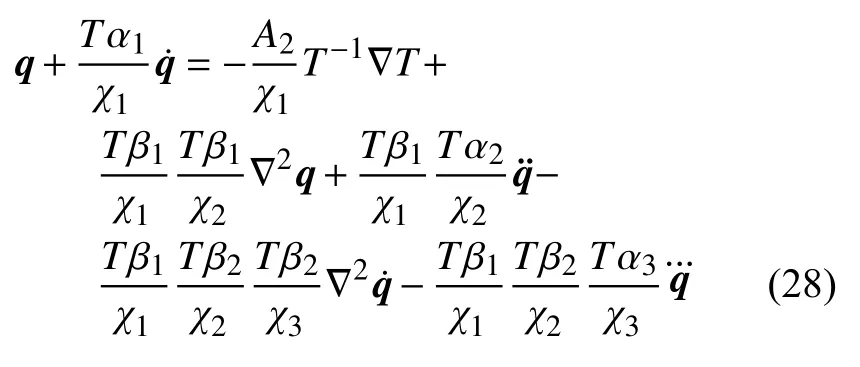
考虑到A1+A2=1,则式(23)可改写为
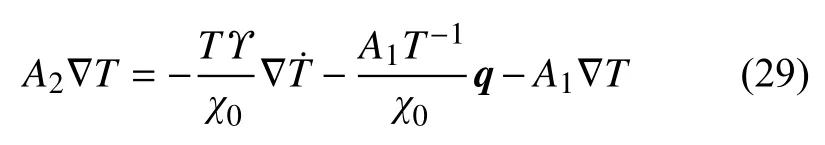
代入式(28)

若取

以及
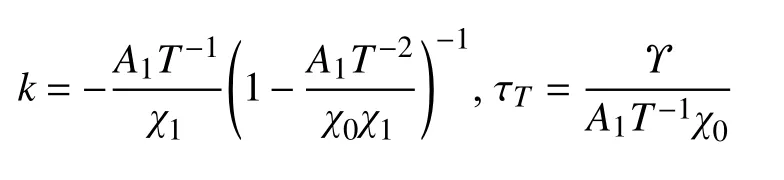
式(30)可更新为
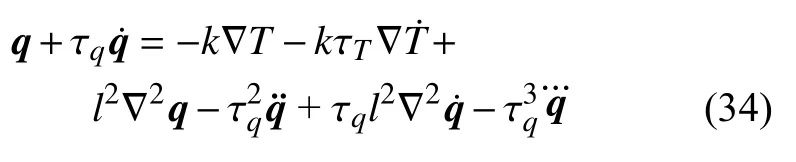
至此,得到了广义热传导方程.虽然,本文中自由能ρψ与应变、温度以及各阶热流相关,但由式(19)和式(20)可看出,应力和熵本构关系具有经典热弹耦合理论的形式.广义热传导方程(34)同时考虑了时空尺度效应,若忽略空间尺度效应,可得
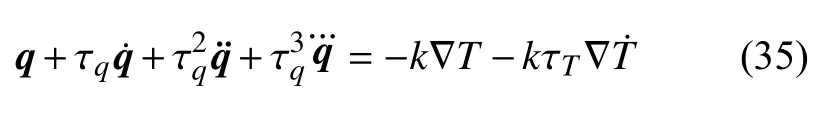
显然,上式可退化为CV 模型(2)、DPL 模型(4)、GN 模型(7)和MGT 模型(9).
2 热学“弹性”单元和“黏性”单元及广义热传导方程的重构
上节中,基于拓展热力学,通过考虑热弹耦合得到了应力、熵本构关系和广义热传导方程.若将其与运动学方程、能量守恒方程和应变-位移关系结合,则可建立广义热弹耦合模型.同时发现,本文得到的广义热传导模型可退化为CV,DPL,GN,MGT 等模型.
为了进一步阐释各模型之间的内在关联,类比于黏弹性力学,本节提出热学“弹性”单元和热学“黏性”单元,并通过串并联方式,实现各广义热传导模型的重构.为此,在一维问题中,考虑GN 模型(5)中热位移χ的概念(=T),热位移梯度记为 ω=∇χ,则傅里叶定律(1)可写作

GN 模型(5)中若忽略k∇T项,可得

类比于力学,称式(37)为热学“弹性”单元,式(36)为热学“黏性”单元.其中q为热流,k*和k分别为热学“弹性”单元和热学“黏性”单元的传热系数,满足关系式k*=k/τ .基于以上单元,现通过串并联模型,揭示广义热传导模型间的关联.基本模型如图1 所示.
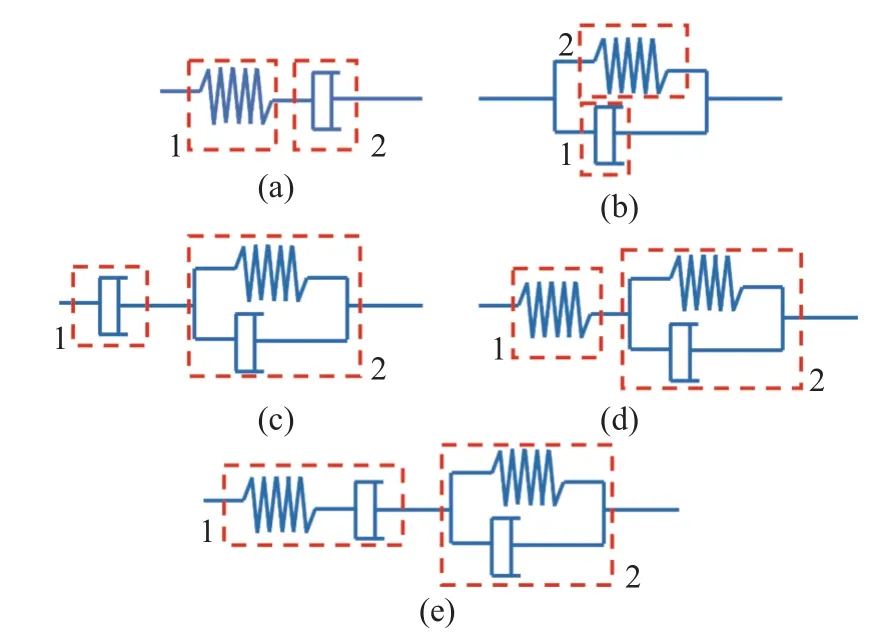
图1 热学黏弹性单元组合模型Fig.1 Combination model of thermovisco and thermoelastic elements
2.1 CV 模型
如图1(a)示,热弹性单元和热黏性单元串联组合,其结构与黏弹性理论中的Maxwell 模型一致.模型两端的热流相等,即

而模型的总热位移χ为各单元热位移之和,则

对式(39)求导

其中
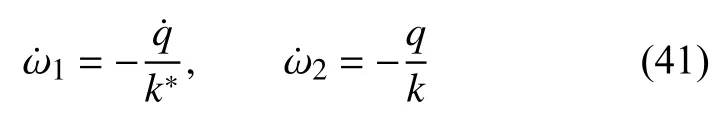
因此

整理后可得CV 热传导模型

2.2 GN 模型
如图1(b)示,热弹性单元和热黏性单元并联组合,其结构与黏弹性理论中的Kelvin 模型一致.模型的热位移与各单元的热位移相等,而总热流为各单元热流之和
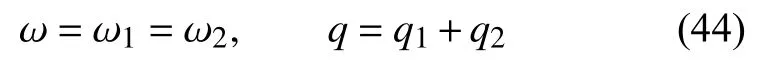
可得到
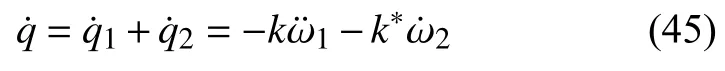
整理后可得GN 热传导模型
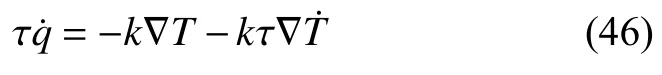
2.3 DPL 模型
如图1(c)所示,两端总热流和各部分的热流相等,总热位移为各单元热位移之和
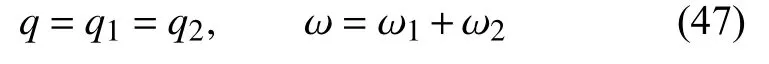
对第1 部分有

对第2 部分有
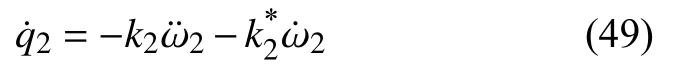
联立式(47)~式(49),可得
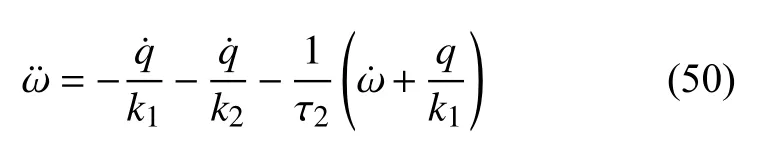
整理可得DPL 型热传导方程
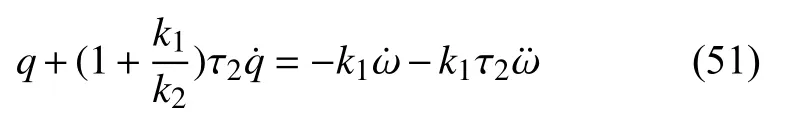
进一步,若设定第1 和2 部分的单元参数一致,即k=k1=k2,τ2=τ,方程改写为
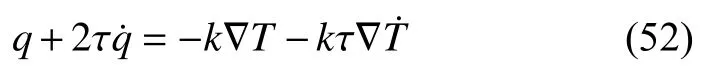
值得指出的是,该方法推导出的DPL 模型是特殊形式,和一般形式(具有两个松弛时间,热流相松弛时间 τq和温度梯度相松弛时间 τT)存在差异,这是因为推导过程中假定了两个黏性单元参数保持一致.
2.4 MGT 模型
如图1(d)示,两端总热流和各部分的热流相等,总热位移为两部分之和
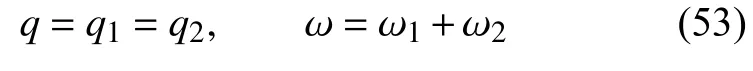
对第1 部分有

对第2 部分有
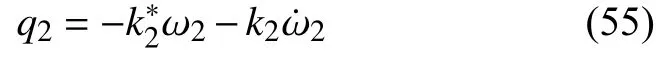
联立式(53)~式(55)可得
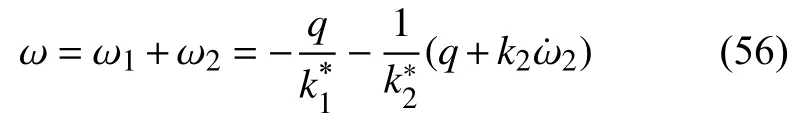
其中
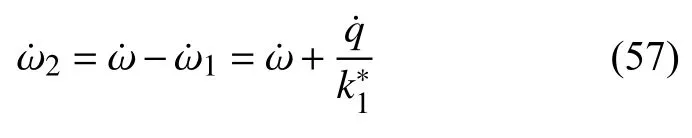
联立式(56)和式(57)有
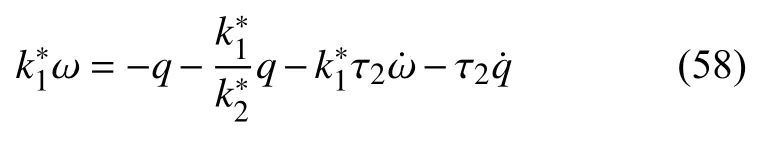
同样地,若k=k1=k2,τ2=τ,,则式(58) 整理为
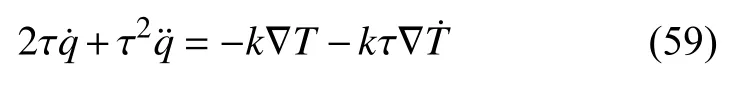
虽然式(59)和MGT 方程的一般形式仍有差别,但两式都是由等分别作为函数构成的等式,仅仅是系数的差异.而这一问题可以通过对常系数的赋值加以解决.事实上,区分热传导模型也可以通过对比所含的函数这一方法来完成.
2.5 新模型——热场Burgers 模型
基于以上的组合思想,自然可以形成一种新的模型.如图1 (f)示,该模型在结构上是由Maxwell 模型和Kelvin 模型串联组合形成,与黏弹性理论中的Burgers 模型的结构一致.在前文推导的基础上,可以直接得出第1 和第2 部分的方程分别为
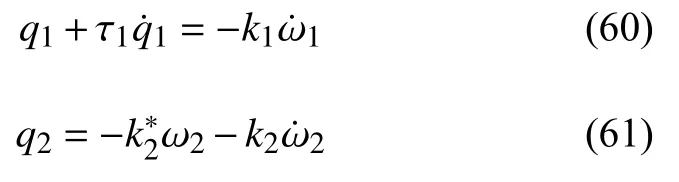
而对于该模型,两端总热流和各部分两端热流仍然相等,总热位移为各部分热位移之和
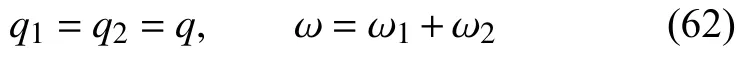
联立式(60)~式(62)并求导可得

至此,通过热学“弹性”和“黏性”单元的串并联组合,重构了CV,GN,DPL,MGT 热传导模型,并通过Burgers 模型得到了第1 节基于拓展热力学的广义热传导模型.特别指出的是,串并联模型给出了广义热传导方程中各松弛时间的关系.综合2.1~2.5 节的推导,广义热传导各模型的控制方程如表1 第2 列所示.

表1 广义热传导模型的变换和统一化Table 1 Transformation and unification of generalized heat conduction models
3 算例计算
考虑一维半无限的材料受边界热冲击和移动热源的作用,假设无穷远处不受扰动,且左侧边界无应力,因此,边界条件可表达为
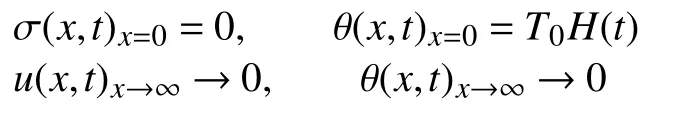
其中,θ=T-T0为温度变化值,T0为起始温度,H(t)为Heaviside 单位阶跃函数,u为位移.一维问题下,运动平衡方程为

考虑了热力耦合的应力本构方程为

其中,λ 和 μ 是拉梅常数,αθ是热膨胀系数.几何方程为

能量守恒方程为
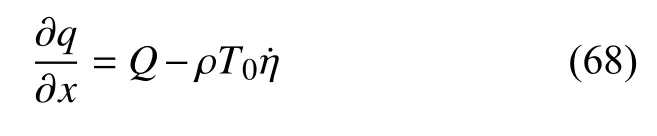
其中Q为热源.熵本构方程为
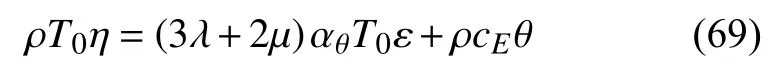
为简单起见,表1 中的广义热传导方程统一写为

其中,M和N是微分算子,如表1 第2 列所示: 对于CV 模型,有M=1+τ∂t,N=1 ;对本文新建模型,有M=1+3τ∂t+τ2∂tt,N=1+τ∂t.热传导方程经拉普拉斯变换后的变换方程如表1 第3 列所示.
联立式(65)~式(70),可得位移和温度的控制方程
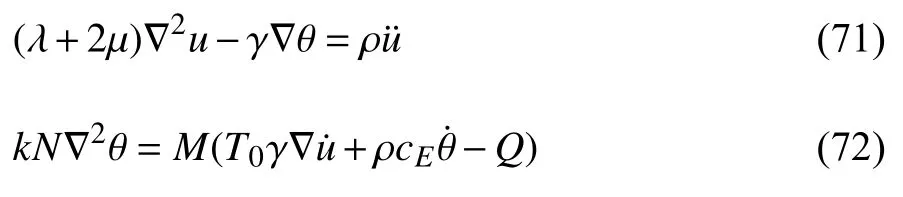
定义无量纲变量如下


其中
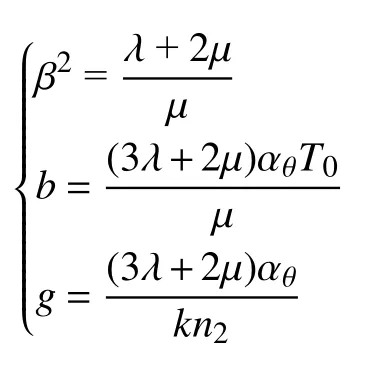
本文运用拉普拉斯变换方法求解这一问题,为此对式(73)~式(75)做拉普拉斯变换,可得
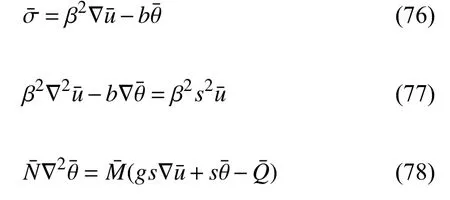
其中,变换后的M和N(即和) 如表1 第4、5 列所示.联立式(77)和式(78)可得
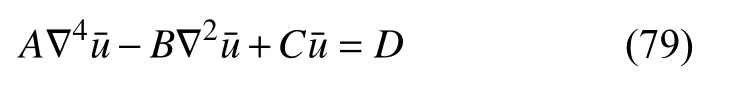
其中

至此,可以通过设定不同的热源函数求解不同条件下的式(79).
3.1 热源函数=0
式(79)退化为
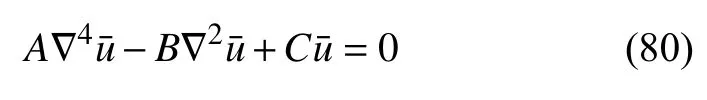
该方程的特征方程有4 个根,考虑到一维半无限问题下,无穷远处不受扰动,故舍去两个正根.位移、温度、应力解的形式为

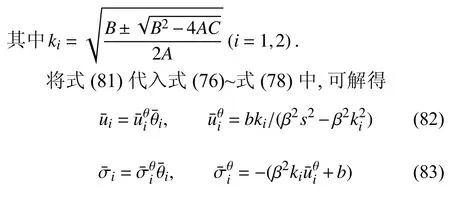
边界条件经拉普拉斯变换后为
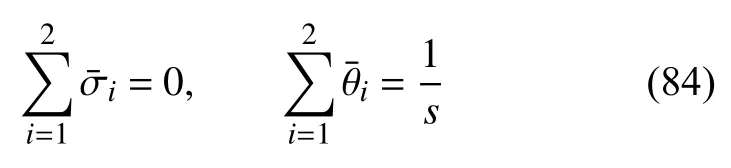
联立式(82)~式(84),可得方程组

联立式(83)和式(85),可解得温度表达式为

3.2 移动热源=L(Q)=
式(79)具体表示为

拉普拉斯域中的温度、应力解同样可表示为
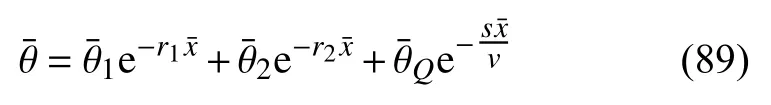

将式(88)和式(89)代入式(76),可得

联立式(76)、式(88)、式(91)和式(92),可解得
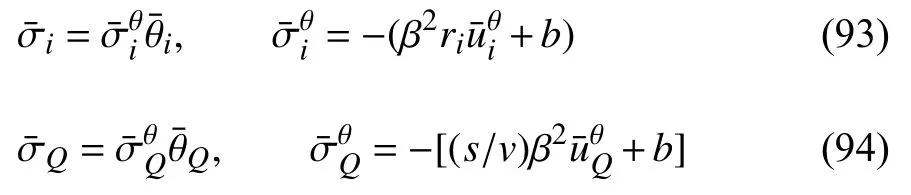
边界条件经拉普拉斯变换为
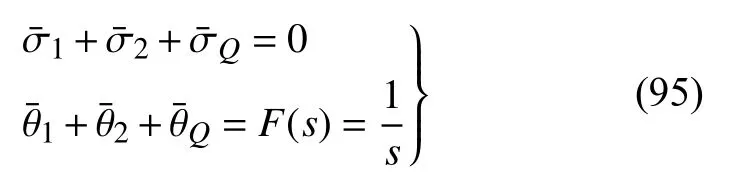
联立式(94)和式(95),可得
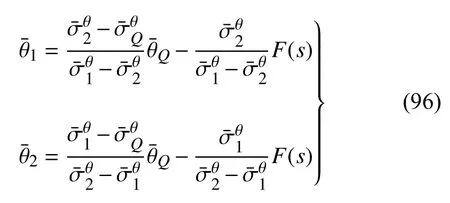
其中

4 结果与分析
在上一节中对问题进行了描述并给出了数值方法.本节将对所得数据进行讨论.(1)在无热源的情况下,将对四个基本模型和新模型的温度、位移、应变响应进行对比;(2) 在移动热源下的各模型温度、位移、应变响应对比;(3)对比不同热源移速下x=0.12处DPL 模型和新模型温度、位移、应变的时间演化特征.材料常数如表2 示.

表2 材料常数表(铜)Table 2 Material constants (copper)
通过对M和N的不同赋值可以实现不同模型的转化,由此可以计算得到无热源状态下各模型t=0.06时刻的空间响应如图2 所示.图2(a)为无热源状态下各模型位移响应的空间分布特征.新模型表现出相比于其他模型更为激进的变化,而GN 模型则更趋保守.具体为: 新模型会发生更大的峰值位移,同时位移在空间上递减更快,至热波边界x=0.3处为0,变形区域更小.相反地,GN 模型产生最小的峰值位移响应,位移递减的曲线也最为平缓,变形区域最大.图2(b)为无热源状态下各模型应力响应的空间分布特征.各模型均在约产生突变,CV,MGT和新模型在约x=0.3,即热波边界处产生突变,x=0.3处以外的区域热波尚未到达,不产生应力响应.而GN 和DPL 模型并没有清晰的波前突变,反映出光滑连续的分布特点.新模型相比于CV 和MGT 模型在波前产生的应力更小.图2(c)为无热源状态下各模型温度的空间分布特征.与应力特征类似,CV,MGT 和新模型在约x=0.3,即波前处的温度并不连续,热边界条件对x=0.3 以外的区域不产生温度影响.新模型在波前的温度响应更小,而GN 和DPL 模型的温度分布光滑连续,逐步归于无响应.综合以上信息,新模型在热波到达时,位移与应力响应峰值更大,但响应区域更小.新模型和CV,MGT 模型均有明显的波前突变,在热波未达区不产生响应,但新模型的波前突变更小.GN 和DPL 模型则呈现光滑连续的变化,响应区域更大.

图2 无热源下各模型位移、应力、温度响应Fig.2 Displacement,stress and temperature responses of each model without heat source
在移动热源移速v=2 的作用下,各模型位移、应力、温度的空间分布如图3 所示.图3(a)为移动热源下各模型位移响应的空间分布,相比于无热源状态,各模型的位移均有较大增加,尤其在x=0.12处即移动热源作用处,位移达到最大值.新模型仍然具有各模型中最大的位移,同时位移在空间上的递减也更快,变形区域最小.图3(b)为移动热源下各模型应力响应的空间分布,热源作用下的应力峰值相比于无热源状态明显增大.无热源状态下的应力峰值约为0.05,移动热源下的峰值应力已跃升至约0.125,且应力峰值出现在移动热源作用处.新模型表现出最大的峰值应力,而GN 模型应对热源作用产生的应力变化则最小.图3(c)为移动热源下各模型温度的空间分布.热源作用下必然会引起各模型温度峰值的上升,其中尤为明显的是CV,MGT 和新模型.其温度曲线也在,即波前处发生突变,回复为常温状态.GN 和DPL 模型的温度曲线是光滑连续的,温度沿空间逐步降至常温,故温度变化的区域更广.由于移动热源的作用,导致各模型无论在波前、波后均产生更大的位移、应力和温度响应,同时在移动热源作用点x=0.12 处相比无热源情况明显升高.同无热源状态的响应特点相似的是: CV,MGT 和新模型在波前的响应也存在突变,新模型的突变更小.与无热源状态的响应特点不同的是: CV,MGT 和新模型在热源作用点x=0.12 处也产生了突变,GN 和DPL 模型无论在热源作用点和波前处,均呈现光滑连续的变化特点.
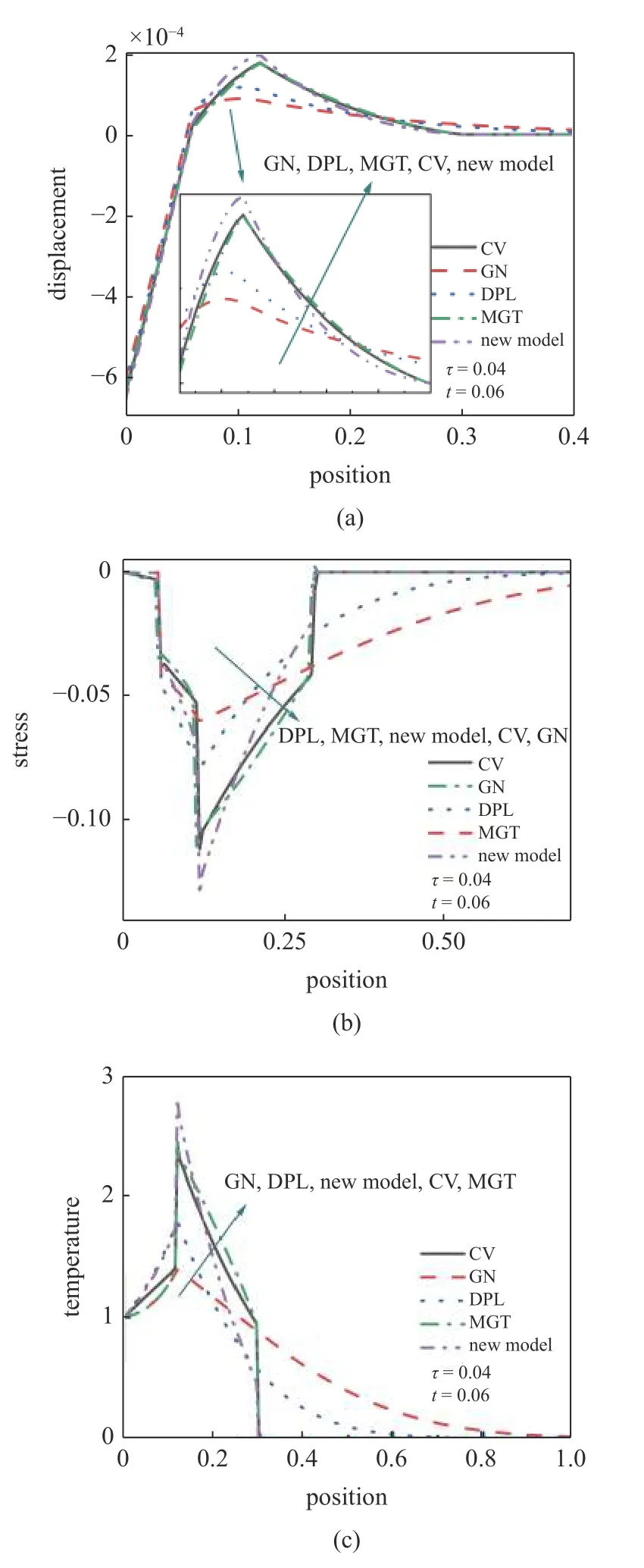
图3 移动热源下各模型的位移、应力、温度响应Fig.3 Displacement,stress and temperature responses of each model under moving heat source
DPL 模型和新模型在x=0.12处受v=2和v=4的移动热源作用,移动热源到达该点的时间分别为t=0.06和t=0.03,其时间演化特征如图4 所示.图4 (a)为该作用环境下位移随时间演化的规律.两模型均在经历过移动热源的加热后产生较大位移,其中v=2热源作用下的位移响应更大.
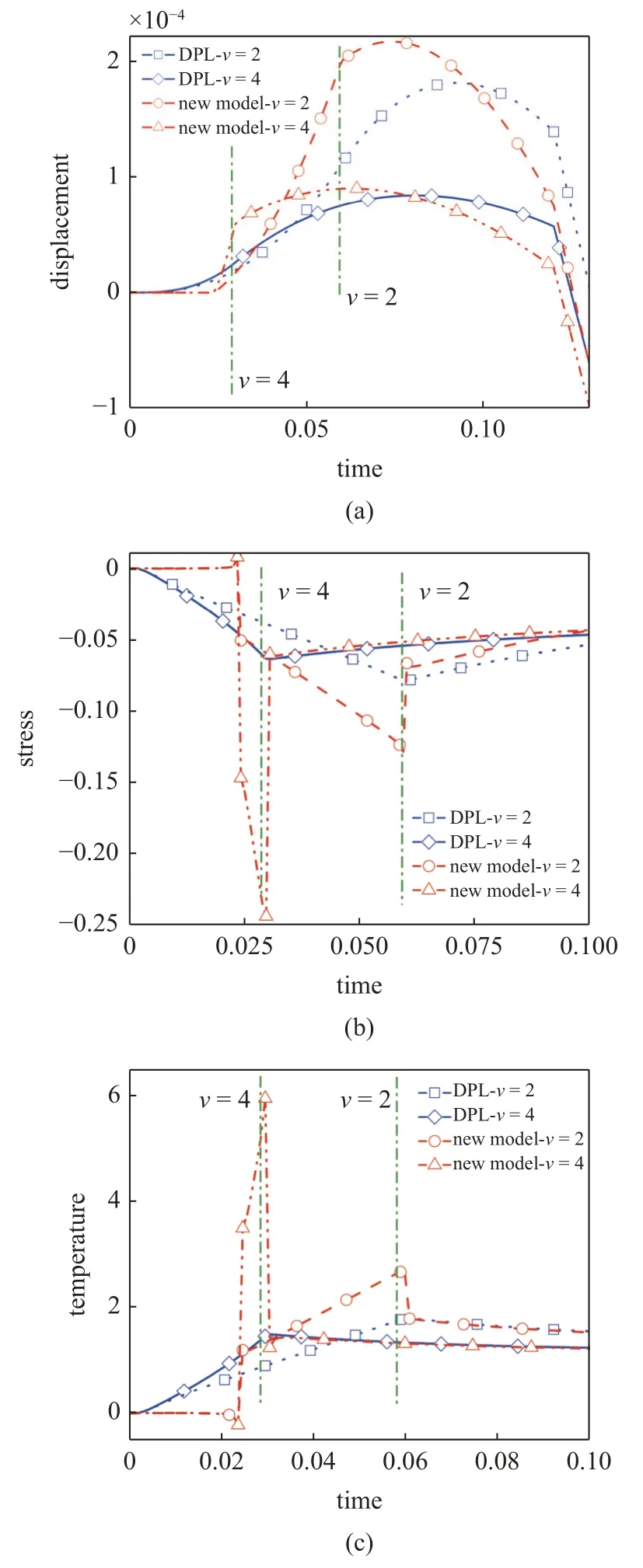
图4 移动热源下DPL 模型和新模型位移、应力、温度的时间演化特征Fig.4 Evolution laws of displacement,stress and temperature of DPL model and new model under moving heat source
新模型的位移响应较DPL 模型峰值更高.图4(b)为DPL 和新模型的应力时间演化曲线.由于移动热源的加热作用,DPL 和新模型均在热源到达时取得极值.新模型具有比DPL 模型更大的峰值应力.在移动热源离开该点后,新模型的应力响应迅速回复至与DPL 模型相近的水平.图4(c)为该作用环境下温度的时间演化曲线.与图4(b)类似,DPL 和新模型经历热源作用后,温度均有明显上升.在温度上升阶段,新模型表现出比DPL 模型更大更快的变化,拥有更高的峰值温度.新模型的温度回复也较快,与应力时间演化曲线呈现的特点一致,新模型在受热源作用前后产生了突变.离开移动热源作用后,新模型的温度响应迅速回复至与DPL 模型相近的数值,之后两模型以较为近似的曲线缓慢下降.热源移速的变化,使得各项数据的达峰时间随移速的增大而提前.在时间演化特征曲线上,可以明显看到新模型在热源作用时产生的响应突变,而DPL 模型则呈现为光滑连续的变化,这一点和空间响应呈现的特征是一致的.
5 总结
超快热冲击等极端热作用环境下,以傅里叶定律为代表的经典热传导理论不再适用,为发展非平衡态热弹耦合新理论提出迫切需求.学者们通过拓展经典热传导方程,已提出多种广义热传导模型,并通过热力耦合建立了广义热弹性理论.为了阐清已有各模型间的内在关联,并进一步发展极端热弹耦合理论,本文基于拓展热力学原理,建立了考虑高阶项的广义热传导理论,其可退化为已有相关理论.同时,类比于黏弹性力学理论,本文抽象出热学“弹性”单元和“黏性”单元模型,基于串并联方式实现了已有各广义热传导方程的重构,并通过Burgers 模型得到了本文新建立的热传导方程,又利用拓展热力学原理,在原理层面上推导支撑了新模型的理论基础.广义热传导方程的重构过程也揭示了部分模型中,热流率相与温度梯度率相的松弛时间的比例关系.如对DPL 模型而言,热流率相与温度梯度率相的松弛时间的比例为2:1.数值结果表明: 无移动热源作用时,新模型得到的位移、应力、温度响应峰值更大,影响范围较小;在移动热源作用下,新模型预测的响应峰值明显升高,且高于其他模型.对比DPL 模型,新模型在拥有DPL 模型双相滞后特点的同时,解决了热波速度无限大的悖论,在响应曲线上反映出清晰的波前突变.本研究将推动远离平衡态极端热弹耦合理论的发展,并为相关问题的求解提供了分析方法.

