针对典型凹腔结构的三维柱面精准成像算法

司炜康 诸葛晓栋 苗俊刚

（北京航空航天大学电子信息工程学院 微波感知与安防应用北京市重点实验室,北京 100091）

引 言

微波成像技术是对目标微波波段的散射或辐射场进行探测并通过成像算法重构出目标图像的技术.凭借近年来微电子技术的不断进步和相关成像理论研究的不断深入，各种高分辨率微波成像设备已被广泛应用于近距离探测应用中.微波成像技术受天气影响较小，能够全天时、全天候工作，且具备一定的穿透能力，受到了包括公共场所安检成像[1-2]、探地雷达[3-4]、无损检测[5]等多个领域的青睐.但是，现有的成像理论出于简化模型的目的，都将目标视为彼此独立的散射点来进行图像反演，忽略了电磁波在目标内部的多次反射过程，简单的点散射理论模型与复杂的实际传播情况间的出入导致了传统成像结果往往伴随着强烈的图像伪影，尤以面对复杂凹腔目标成像时最为严重.在安检成像领域中，已经注意到了相关问题[6].由于电磁波在人体四肢与躯干间的多次反射，小臂下方及双腿之间的伪影为后续的精准检测与识别造成了极大的困扰.因此，解决包含多次反射特性凹腔目标的精准成像问题是微波成像技术实现广泛应用的一个关键.

在微波成像与检测领域，探测信号的多次反射效应带来了两类问题.第一类中，电磁波的耦合发生在目标和环境之间，如穿墙雷达等室内成像应用，墙体和地面对探测信号的反射多会导致伪目标的出现，致使对观测目标的数量和位置估计出现偏差[7-8].由于这种类型的图像干扰通常不会与目标真实位置混叠，因此学界通常着眼于利用干扰抑制[9]或目标精确提取技术[10]来解决这类问题，包括阵列测试或极化测试手段，都能有效地提升检测、识别精度.与第一类问题不同，第二类问题面对的是来自目标自身结构内部的多次反射.由于电磁波在目标内部的耦合，致使目标成像结果发生严重形变，具体表现为与目标真实结构位置临近甚至重合的伪影，以及目标真实轮廓的大面积缺失.对于这类问题，已有学者提出了多种精确路径补偿方法，在一定程度上扩展了成像范围[11-12].其中比较具有代表性的距离点徙动(range points migration,RPM)算法适用于大多数凹腔结构，且不需要额外的积分计算，具有十分高效的运算效率[13].然而受限于实际测试中多次反射过程的复杂性，通常仅有二次反射路径是可求解的[14].

本文主要致力于探究第二类问题，即电磁波在被测目标内部耦合所产生的图像伪影问题.传统成像理论中通常采用波恩近似 (Born approximation)假设来简化散射过程的描述.在波恩近似假设中，认为目标自身的散射场强度远弱于入射场，忽略了多次反射对总散射场的贡献.该假设对于简单凸体目标是成立的，但对于具备对称结构的凹腔目标来说，其多次反射分量不仅不能忽略，有时其强度还能与入射场相比拟.正是由于传统成像对多次反射信号传播路径差异的忽略，导致了凹腔目标成像结果中伪影的出现[15].二面角作为一种简单且典型的凹腔结构，广泛存在于各种应用场景，可以被视为组成更复杂凹腔结构的一个基本元素.图1 展示了45°二面角的传统柱面合成孔径(cylindrical aperture synthesis,CAS)成像算法结果，二面角边长0.2 m、高度0.3 m，圆柱测量半径为0.6 m，其中各平面视图均为最大值投影.从图1 成像结果可以看出，此时的成像伪影包含了两种：一种是位于二面角交线位置的强散射点，另一种为45°真实二面角结构外侧的两条夹角更大的短边.这些伪影导致了目标真实轮廓图像的动态范围降低和结构的严重畸变.在之前的工作中[16]，我们已经提出了一种有效的二维凹腔目标精准成像算法.本文将在之前工作的基础上，将该算法扩展至三维空间.

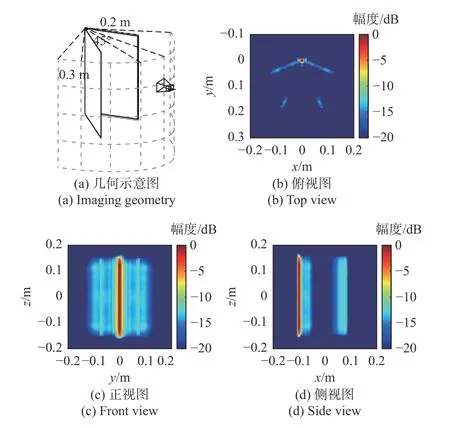
图1 柱面成像几何示意图和传统CAS 算法对45°二面角成像结果Fig.1 Illustration of cylindrical imaging geometry and reconstruction of dihedral (with 45° opening angle) using a conventional CAS algorithm

1 典型凹腔目标精准成像算法原理

对于雷达成像来说，成像系统接收的是目标对入射波的散射场，因此为了分析伪影的成因，首先需要建立正确的凹腔目标散射模型.为了表征电磁波在腔体内部多次反射的过程，借鉴弹跳射线(shooting and bouncing rays,SBR)理论中的一些经典概念，使用射线传播来近似表征电磁波的辐射过程，从而简化多次反射过程的分析，便于探求伪影形成的规律.为使上述假设成立，通常要求被测目标为电大目标，即

式中：k为信号波数；a为目标口径长度.

根据SBR 中的相关理论，将信号的传输过程分为两个部分.第一部分包含了电磁波从发射天线和在凹腔内部多次反射的整个过程，传播路径记为d1.在该过程中使用射线追踪法，路径长度的计算符合镜像原理.第二部分为信号离开凹腔目标向自由空间辐射，对应的传播距离为出射前与凹腔结构最后一次反射点至接收天线间的距离，记为d2.这两部分传播距离之和d1+d2即为需要补偿的总传播路径.

在三维空间中直接对多次反射特性进行分析是较为复杂的，为了解决这一困难，首先将射线路径分别投影到xoy与yoz平面，并结合之前的工作导出电磁波在二面角目标内部的三维传播公式.如图2(b)所示，在xoy平面内，电磁波从点Axoy(r0,θ0)发射，并经过多次反射后到达最后一次反射点Cxoy(r,θ)处.对于二面角类结构，其最大反射次数Nm仅取决于二面角的开角 2φ[15]：

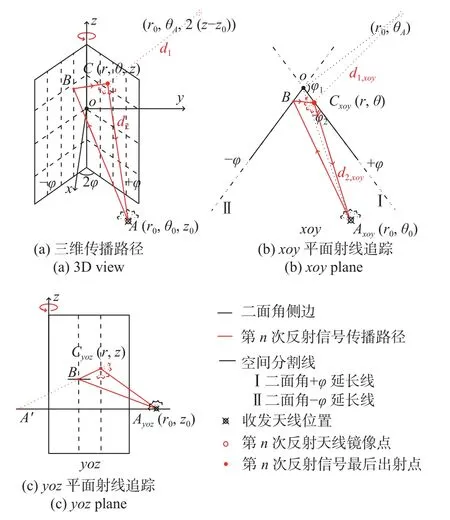
图2 基于三维圆柱测量条件的二面角成像几何示意图Fig.2 Imaging geometry of concave structure based on 3D cylindrical measurement

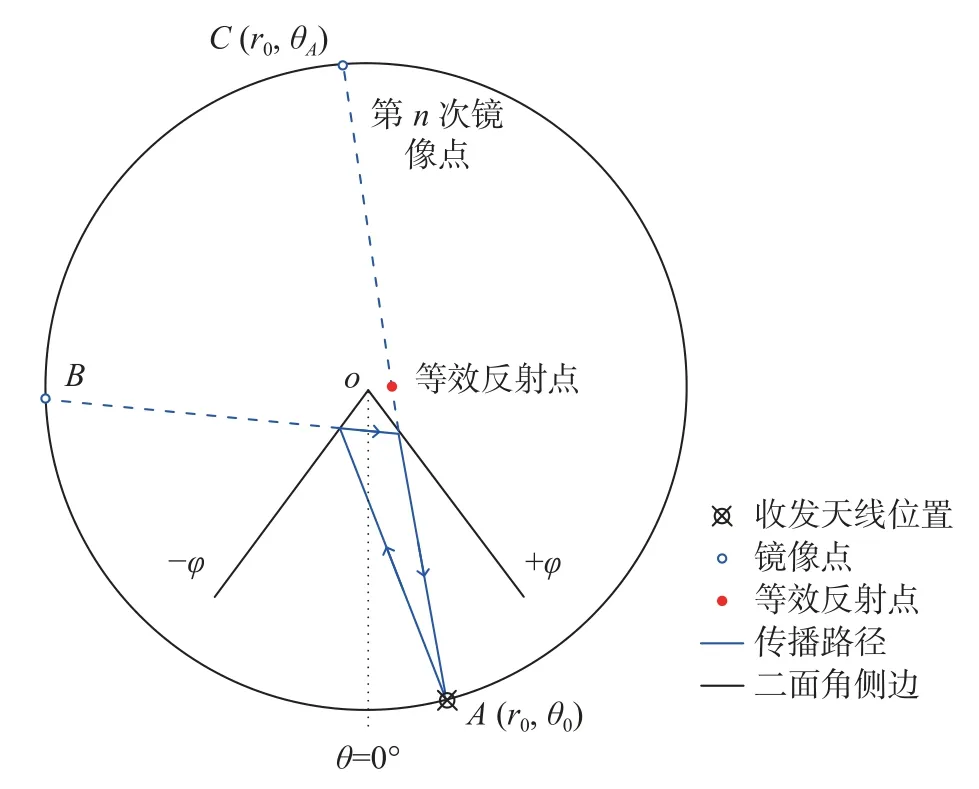
图3 射线在xoy 平面上的镜像反射方法示意图Fig.3 Schematic of the mirror reflection method on xoy plane

这里我们使用 θA表示A点的第n次镜像点.根据镜面反射原理，如果第一次镜像点 θA1与原物点关于θ边对称，则 θA1与θ 之和为 2θ；第二次镜像点与第一次镜像点关于边 -θ对 称，则 θA2与θA1之和为 -2θ.依次类推，最后一次反射点 θA可表示为

式中，θ=±φ.在图3 中，点A和点C之间距离中点可看作为等效的双程散射点，显然由于多次反射原因，等效反射点的位置将偏离二面角的真实结构位置.

根据上述分析，可以进一步导出二面角的正向散射模型.在图2(b)中，φ1为镜像点、原点连线与最后一次反射边间的夹角，φ2为接收天线、原点连线与最后一次反射边间的夹角，可分别表示为：

因此，可推导出传播路径d1和d2在xoy平面的投影d1,xoy和d2,xoy为：

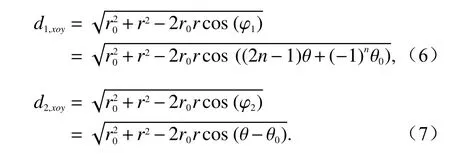
式中，r为二面角上一点到z轴的距离.

而在yoz平面上，点Ayoz(r0,z0)和 点Cyoz(r,z)之间的纵向距离并不会随着多次反射而改变，三维传播路径d1和d2可表示为：

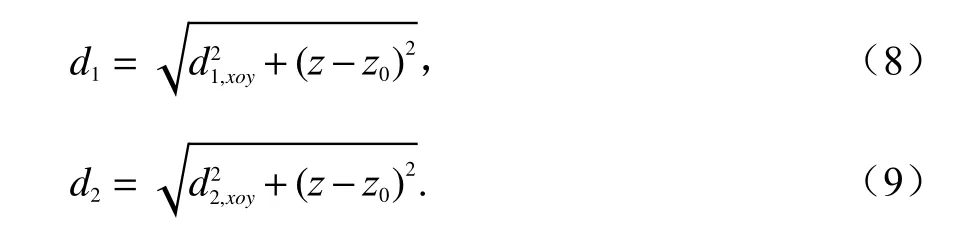
因此，可以建立二面角目标的正向传播模型为

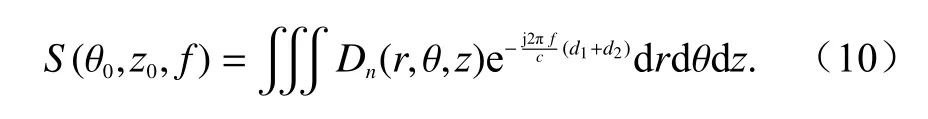
基于反向投影(back projection,BP)思想，离散化的反向求解模型如下：

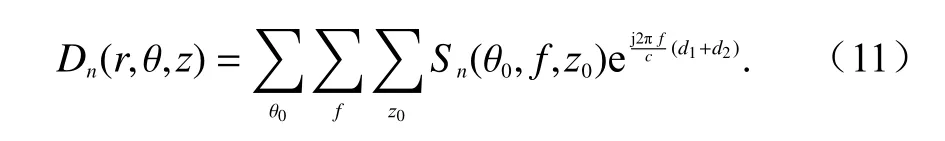
除了准确的反向模型以外，针对包含多次反射特性凹腔目标的精准重构还有赖于对不同反射次数信号的准确分离.这种操作可以通过圆极化测量来精确实现[17].由于圆极化信号的极化在入射到光滑反射表面后会发生反转，因此相同圆极化特性的收发天线仅能收到奇数次反射信号，而不同极化特性的收发天线仅能接收偶数次反射信号.在对奇数次、偶数次信号进行分离以后，通过二者的图像，可以进一步迭代分离各个反射次数的信号.

信号的分离步骤过程(图4)如下：首先通过偶次反射数据In和传统成像算法得到的奇次反射信号图像I0确定最大偶次反射次数.以45°二面角为例，在奇次反射信号的传统成像结果中，包含开角为45°的真实二面角图像和开角为45°×3=135°的二面角伪影图像.而对于偶次反射信号，仅有最高次能够被接收到[15]，对偶数次信号按n=2,4,6,···通过式(11)进行重构，得到的偶次图像In中二面角的开角分别为90°,45°,30°,···.In与I0相似度最大时所对应的n值即为最大偶次反射次数，图5 给出了确定最大偶次反射次数的示意图(以xoy切面为例).

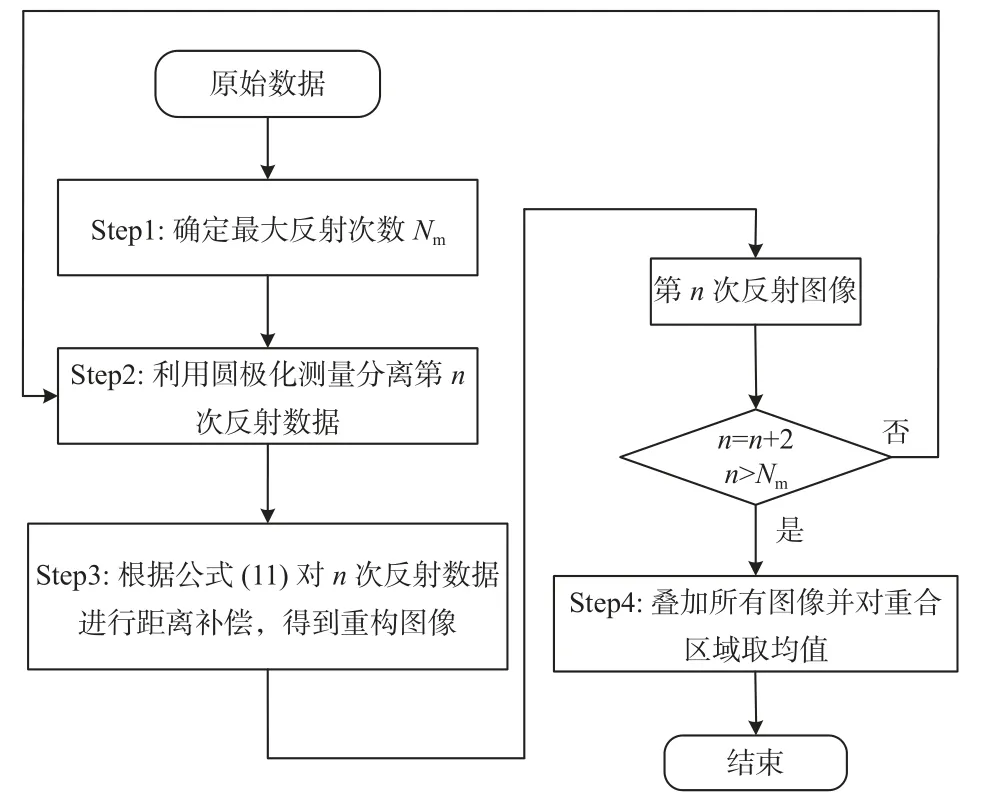
图4 针对多次反射特性的精准成像算法流程Fig.4 Flowchart of proposed image reconstruction algorithm considering multiple scattering

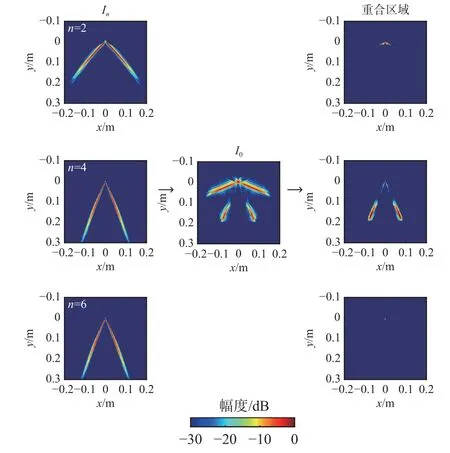
图5 确定最大偶次反射次数过程示意图Fig.5 Process of determining the maximum even reflection times

在确定了最大偶次反射次数后，其对应的偶次图像为我们提供了一个可用的图像滤波窗口，依次按照n=1,3,5,···对奇次数据进行重构，并利用偶次图像分离其与各奇次图像的重叠区域，再利用式(10)回推至频域，最终得到分离后的各反射次数信号.

需要注意的是，由于凹腔结构的遮挡效应，各反射次数信号可以照射到的区域是不同的.第n次反射信号的区域如下：

例如，在图1 所示的结构中，1 次反射信号可以照亮的区域为0.14～0.2 m，3 次信号可以照亮的区域为0～0.2 m，如图6 所示.

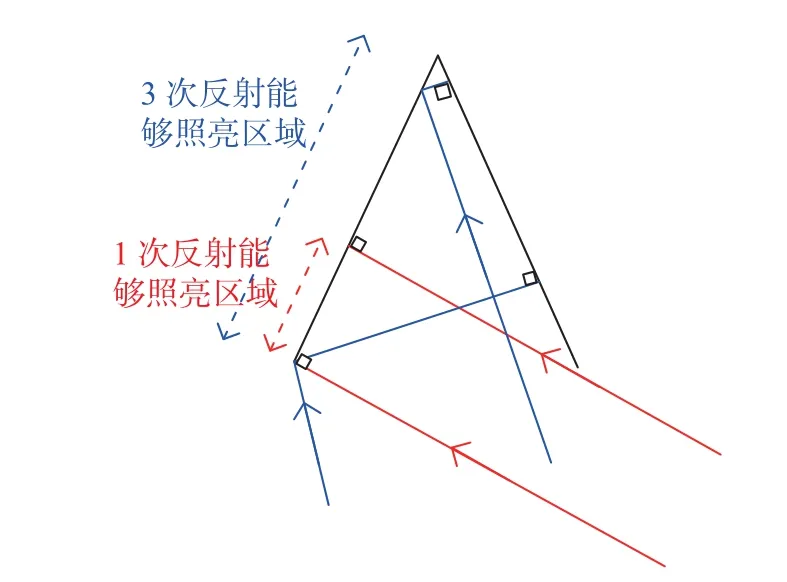
图6 45°二面角1 次、3 次反射照射区域示意图Fig.6 The illuminated region by 1RT and 3RT signals of 45° dihedral

该情况下，尽管凭借3 次信号就可能重建出整个目标轮廓，但1 次反射信号也包含了二面角靠外区域的信息.因此，最终图像通过对所有反射次数图像叠加而得到，并且需要对重叠区域图像取均值以避免该区域的幅值倍增.均值计算式为

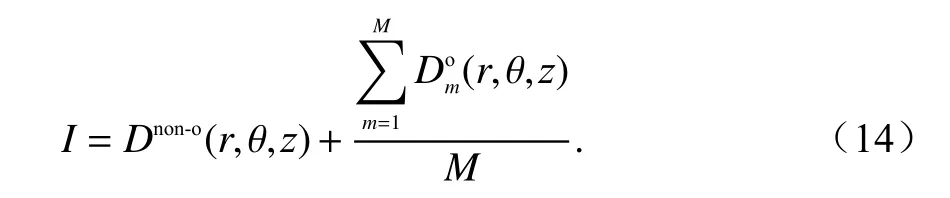
式中：Dnon-o和Do分别表示非重叠区域和重叠区域图像；M为重叠图像数量.

2 仿真与实验结果验证

2.1 算法仿真与分析

在本小节中，通过仿真验证所提出算法的性能.仿真的二面角目标如图7 所示，二面角高度0.3 m、边长0.2 m，并在二面角右半平面剖除了“BH”字母图案.

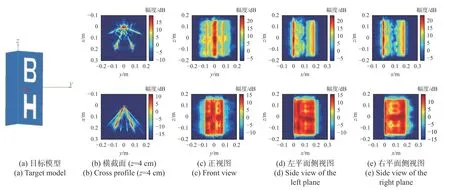
图7 目标模型及使用传统CSA 算法(上)和本文算法(下) 对仿真三维45°二面角数据的成像结果比较Fig.7 Comparison between the imaging results of simulated 3D 45° dihedral data using the conventional CAS algorithm(top) and the proposed algorithm (bottom)

在传统成像结果中，4 次反射信号在二面角顶角区域形成了强散射点，降低图像的动态范围.此外，3 次反射信号还形成了一个开角为135°的二面角伪影，在侧视图中可以看到目标的图像被分成了两个部分.

相较于传统CAS 成像算法，本文所提出的算法不仅能正确地重建物体轮廓，并且保留了大量的图像细节，如图7 第2 行中的右平面测试图所示，剖除的“BH”图案也被精准地恢复出来.与传统的CAS算法相比，重建图像的动态范围提高了约10 dB.为了进一步说明所提出成像算法的性能，使用均方根误差(root mean square error,RMSE)定量评估重构算法精度，结果见表1.

表1 45°二面角两种算法重构的RMSETab.1 Reconstructed RMSE of 45° dihedral with 2 algorithms dB

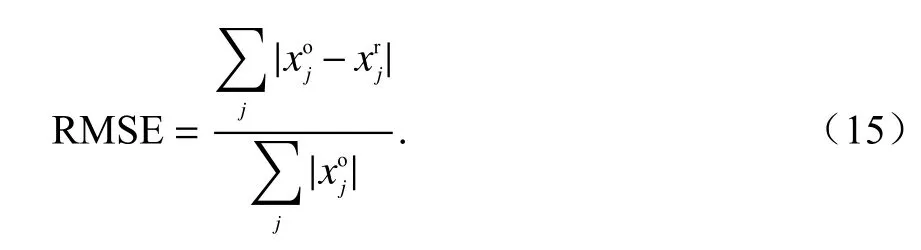
2.2 实验验证

本节通过成像实验进一步验证所提出算法的性能.在第一个例子中，使用两块尺寸为0.3 m×0.3 m的光滑金属平板拼接成一个34°二面角，并在二面角的左平面边缘上粘贴了一层薄膜吸波材料，如图8所示，实验中使用Rohde &Schwarz 生产的ZVA24矢网进行数据采集.实验中使用的测试天线为一对极化相异的圆极化天线(工作频率6～18 GHz)，因此矢网测试S21时连接的收发天线极化特性相反，仅能接收奇次反射信号；测试S11时连接的收发天线极化特性相同，仅能收到偶次反射信号.实验的测试频率为6～18 GHz，频率步进间隔0.1 GHz 二面角的顶点(圆周旋转中心)与收发天线距离约为0.7 m，通过转台完成对目标的圆周扫描.圆周扫描范围为-90°～90°，其中0°对应二面角的中轴线，扫描步进为0.5°.实验中使用较为精细的频率间隔和扫描间隔，以保证成像结果中不会出现方位向和距离向的混叠.对于圆极化天线，其各频点的相位中心偏差较大，为保证重构图像效果，首先测试一组金属球的回波数据用于信号频域响应校准.校准前后的测试数据时域信号如图9 所示.

图8 实验设置和部分包裹吸波材料的34°二面角(例1)Fig.8 Picture of experimental setup and a 34° dihedral partially wrapped by a thin absorbing material

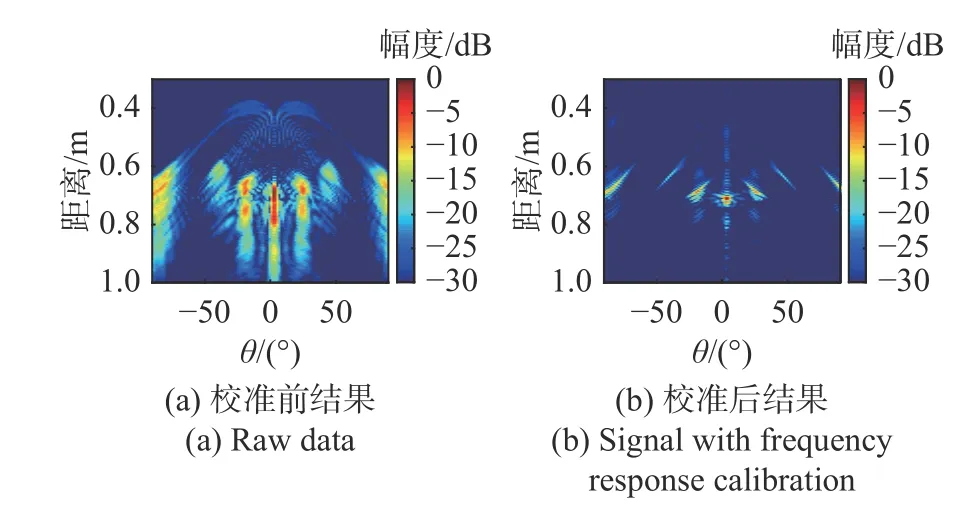
图9 接收信号时域响应Fig.9 Time domain response of received signal

图10 展示了34°二面角传统CAS 算法和本文算法的成像结果.在CAS 成像结果中，除了最下方较短的两条边为真实的目标轮廓，还形成了开角为34×3=102°和34×5=170°的两组二面角伪影.而使用本文所提出的算法，恢复出了准确的二面角轮廓，且成像结果中左平面边缘幅度比右平面边缘更低，符合吸波材料粘贴位置.

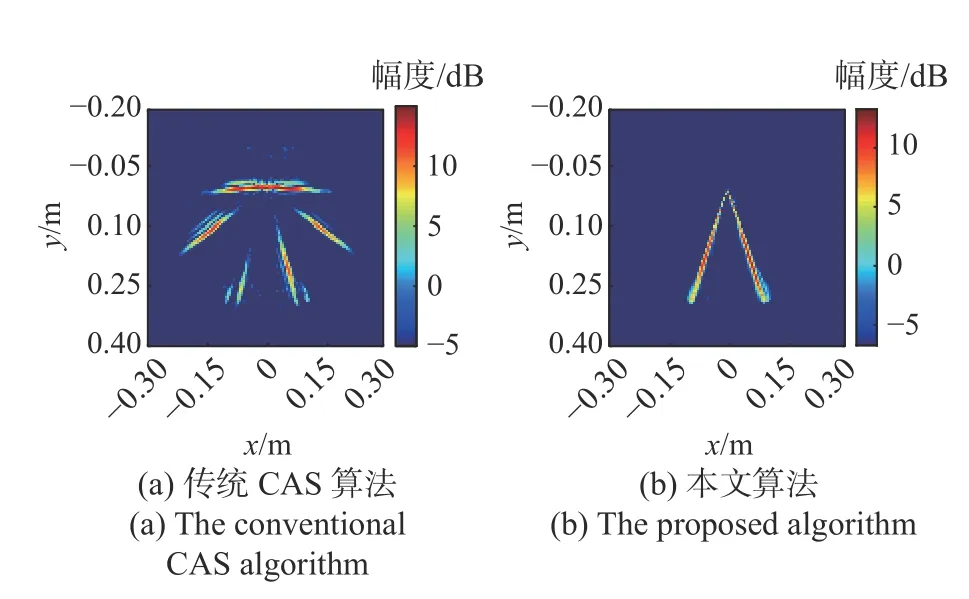
图10 34°二面角两种算法实测成像结果Fig.10 Experimental imaging results of a 34°dihedral with 2 algorithms

在第二个例子中，使用相同的金属平板拼成60°二面角，并在金属平板右侧使用吸波材料拼接出“T”状图案，如图11(a)所示；通过扫描平台和转台协同工作完成柱面数据采集，如图11(b)所示.实验选择与之前相同的频率采样参数，柱面测量的旋转半径约为0.6 m.实验在z方向上采集80 cm 范围的数据，步进间隔为0.8 cm.在水平方向上，圆周扫描范围为-80°～80°，扫描间隔0.8°.

图11 实验设置与测试目标(例2)Fig.11 Experimental setup and measured object (sample 2)

图12 比较了传统三维CAS 算法和本文所提出三维精确成像算法的成像结果.图12(a)展示了z=5 cm 处的横截面图像，由于三次反射信号影响，传统CAS 算法的结果中形成了180°开角的二面角伪影；图12(b)和图12(c)分别展示了通过最大值投影得到的正视图和侧视图.在传统CAS 成像结果的前视图中，也可以观察到“T”字母的大致轮廓，这是由于对于60°二面角，仅三次反射信号就能够照射到完整的内部结构.但如图12(a)和(c)所示，传统CAS 结果中3 次反射图像实际上偏离了其正确位置，这将严重影响对目标的检测和识别.而本文所提出的算法恢复出了更准确的二面角结构，并能更清晰地观察到“T”型图案.

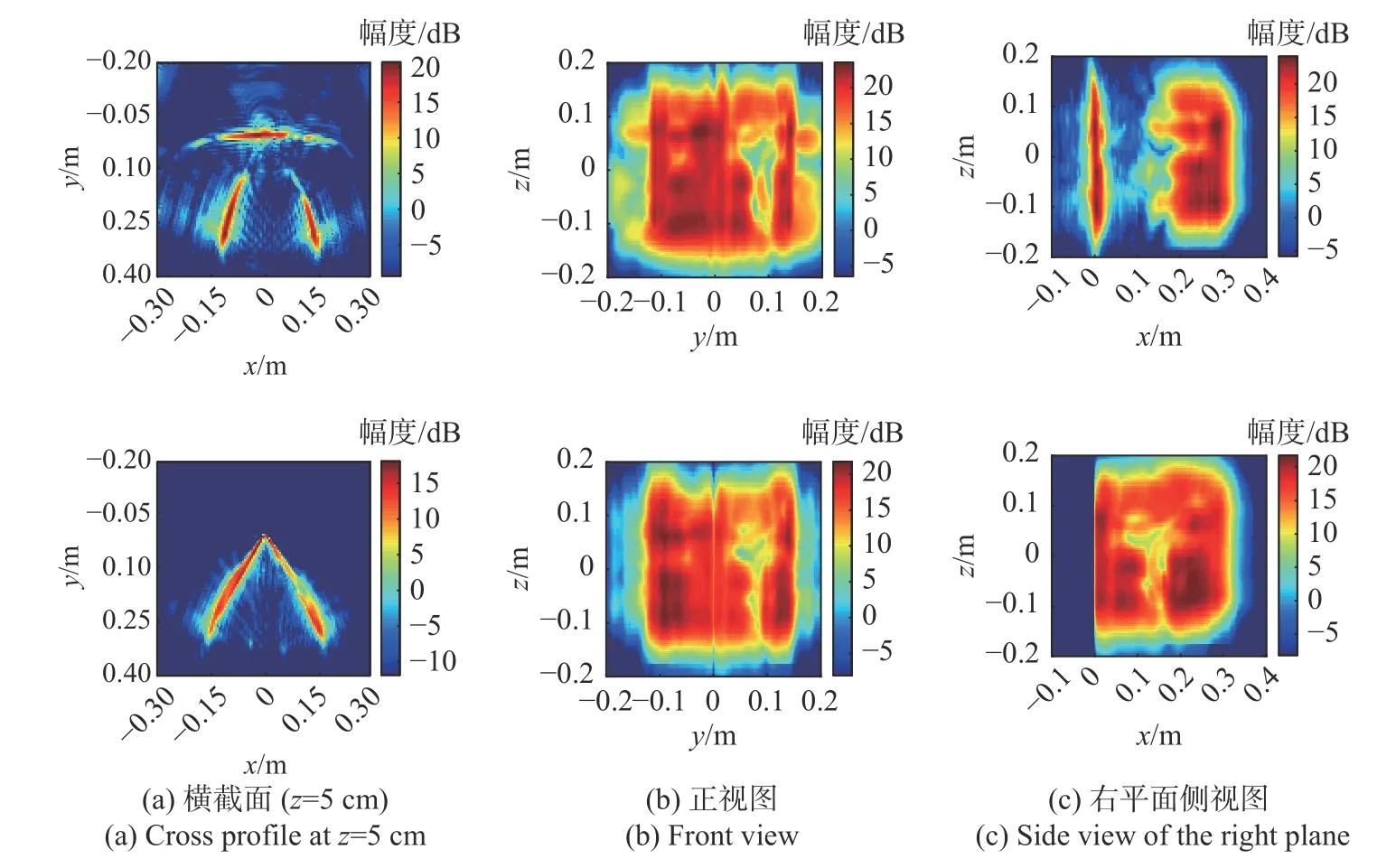
图12 传统CAS 算法(左)和本文算法(右)的实验结果对比Fig.12 Comparison of imaging results of conventional CAS algorithm (left) and proposed 3-D accurate imaging algorithm(right)

对于本文所提出的算法，在实际应用中需要着重考虑二面角的口面尺寸以确定算法的适用范围，一方面需要足够的口面尺寸才能满足电大假设，这是所提出的重构算法能够实施的前提.但大口面又要求更精细的方位扫描间隔以避免方位向的图像混叠，增大了测量开销.除此之外，过小开角二面角(开角小于30°，对应6 次反射)的重构问题不在我们的考虑范围之内.因为在实际中，当开角小于30°时，电磁波经过6 次反射以上的衰减，其强度往往难以被观测到.此外由于此时二面角的口面尺寸很难满足电大假设，也会对重构精度造成影响.除了上述问题之外，其他测量参数的选择与经典成像理论一致.

3 结 论

本文针对凹腔结构成像中的伪影干扰问题，提出了一种针对二面角结构多次反射特性的三维精准成像算法.通过将多次反射信号路径向xoy和yoz平面投影，降低了传播路径的分析难度.结合之前的工作导出了三维路径传播公式，并最终建立了信号的传播模型和图像重构流程，仿真和实验结果均证明了该算法的有效性.作为各类凹腔目标的基本组成单元，对二面角进行研究分析将对未来解决更复杂腔体的成像问题提供有力支持.