被动毫米波三维成像技术初探

孙雪蕾 胡岸勇 诸葛晓栋 苗俊刚

（北京航空航天大学 微波感知与安防应用北京市重点实验室,北京 100191）

引 言

在过去的三十年间，毫米波成像技术在人体安检领域的应用极大弥补了传统安检的不足，为大客流量公共场所的人体安检提供了高效解决方案[1].与传统的金属探测式安检手段相比，毫米波成像式安检技术可检测物品种类多，不仅可以检测金属违禁品，对非金属类的违禁品也能够进行有效检测[2].与X 射线相比，毫米波由于无电离辐射更加适用于人体携带违禁品的检查.利用毫米波成像技术能够检测人体衣物下藏匿的违禁品；同时结合图像处理与图像识别技术，能够实现对人体藏匿违禁品的检测、定位和识别.

利用被动毫米波成像技术，可以实现对观测场景以及观测目标(如人体)辐射亮温分布图像的测量.一般人体表面的辐射亮温分布由两部分构成：一是由人体自身热辐射形成的辐射亮温分布，二是由人体反射来自环境中的热辐射信号所形成的辐射亮温.自然界绝大多数物体由于其表面和内部的结构及介电常数不同，具有不同的发射率、反射率和透射率[3]，当物体处于热力学平衡状态时，具有不同的辐射亮温.因此利用辐射亮温分布图像的对比度差异，可以有效实现对衣物下藏匿的可疑物品的检测和识别.

国内外已有众多研究机构与公司成功研制了二维被动毫米波人体安检成像系统样机[4-6].近年来，北京航空航天大学微波感知与安防应用北京市重点实验室也成功研制了数套通过式被动毫米波人体安检仪[7-12]，最新研制的1 024 通道协同体制通过式毫米波人体安检仪(图1)能够实现25 帧/s 的视频速率成像，温度灵敏度约为4.5 K@25 帧/s.

图1 北京航空航天大学 1 024 通道协同体制毫米波人体安检仪Fig.1 BHU-1 024 Hybrid Passive Imaging System

尽管目前二维被动毫米波成像系统具有成像速度快、成本低的优点，但也存在着成像对比度差、动态范围小的问题，不利于违禁品的检测.尤其是在室内环境与人体温度差异小的情况下，测得人体辐射亮温分布图像对比度差，增加了对违禁品的检测和识别难度[13].借助辐射亮温分布的三维信息，通过人体表层外形轮廓的变化实现对可疑物品的有效检测，有利于提高室内被动人体安检中违禁品的检出率.

近年来，得益于半导体工艺、单片式微波集成电路(monolithic microwave integrated circuit,MMIC)技术和大规模数字相关器技术等的进步，接收机前端的小型化设计、低功耗多通道数字相关器及高集成度数字信号处理的实现为大规模综合孔径辐射计天线阵列的物理实现提供了支持[14].

目前，已有英国学者对基于大规模三维综合孔径天线阵列的被动毫米波三维成像技术开展了研究[15-18]，并通过仿真实验初步证明了被动三维成像的可能性.但该技术应用于人体安检的工程可实现性还需要进一步证明.此外，该技术的实际应用仍面临诸多挑战：1)需要开发快速高性能的精确被动三维成像算法；2)需要对三维阵列天线进行合理布局，尽可能降低天线以及相关器的数量；3)被动三维成像系统的高性能、低成本硬件实现也是一个难点.

本文将主要针对被动毫米波三维成像系统的成像阵列对三维成像效果的影响开展初步的讨论和分析，为最终实现被动毫米波三维成像提供理论依据.

1 被动毫米波三维成像的原理

干涉式相关辐射计可以实现对空间频域可视度函数的采样，从而恢复出空间域的辐射亮温分布信息[19].图2 所示为观测远距离点源相关辐射计的几何关系.其中 A、B分别为两接收天线.空间中的电磁波信号被天线接收后将经过接收机前端被放大并进行滤波，而后两路信号进入相关器进行相关计算得到测量的相关值.相关器由乘法器和积分器构成，能够实现对输入两路信号的相乘和积分运算.

图2 观测远距离点源的相关辐射计的几何关系Fig.2 Geometry of a correlation radiometer viewing a distant point source

若一个单频辐射点源位于接收天线正前方角度为 θ的位置，则输入乘法器两端的信号可分别表示为：

式中：ai是信号的幅度；ni(t)是接收机噪声产生的电压；τg是两个天线接收平面波波前的时间差，表达式为

式中：D是天线基线距离；c是光速.由于信号和噪声统计不相关，因此相关器输出结果为

式(4)被称作条纹方向图，改变D的取值，则可以得到不同的条纹方向图.条纹方向图代表了观测目标空间热辐射功率分布的傅里叶级数分量.

将输入信号用复信号表示，则不同长度基线的相关器输出的复相关值与待测目标空间的热辐射功率分布构成一维傅里叶变换关系.相关测量输出结果为辐射功率分布空间频域的采样结果.因此，对复相关值进行逆傅里叶变换即可得到观测目标空间辐射功率随观测角度变化关系的图像.此时获得的图像仅有方位向信息和辐射功率强度信息，若采用二维平面阵列进行观测则可同时获得方位向和俯仰向两个维度的辐射功率分布信息.

辐射源的距离向信息可以利用双目视觉原理获得.如图3 所示，假设观测目标区域中仅有一个点辐射源存在，利用两个一维成像阵列可分别获得关于点辐射源的两个方位向信息 θ1、θ2.利用这两个方位向信息则可获得点辐射源的距离向信息，从而恢复出点辐射源在空间中的位置，实现被动三维成像.因此要实现被动三维成像，要求成像阵列为三维阵列.

图3 被动测距原理Fig.3 Schematic diagram of passive ranging

利用三维干涉式综合孔径辐射计阵列，能够实现对三维空间频域的采样，再借助三维逆傅里叶变换即可恢复三维空间辐射功率分布，即实现三维辐射亮温分布的反演计算.

从物理光学角度考虑被动三维成像过程，扩展光源I(S)在 空间中任意两个位置产生的电场强度vJ(t)和vK(t)的互强度可表示为[16]

式中：rJ、rK分别为空间两点与扩展光源的距离；σ表示在辐射源表面进行积分.

在旁轴近似条件下，互强度与扩展光源的强度构成一组傅里叶变换对.通过对互强度求逆傅里叶变换，即可恢复出原始的扩展光源强度：

式中：A(l)为 单元天线的方向图；uMIN、uMAX取决于基线长度；u为局部空间频率(local spatial frequency,LSF)；l为由相位中心RPC指向辐射源位置RS的位置矢量，如图4 所示.

图4 三维综合孔径成像坐标系Fig.4 Coordinate system of the 3D aperture synthesis imaging technique

在近距离成像应用中，由于旁轴近似区域大小有限，互强度与辐射源的傅里叶变换关系不再严格成立.为获得较大的清晰成像区域范围，本文采用逐点聚焦成像方法实现对观测目标区域的三维成像.该算法借鉴了目前二维综合孔径辐射计成像中的聚焦成像思想，通过对综合孔径辐射计阵列测量得到的相关值进行相位加权并叠加，从而实现对观测目标场景的逐点聚焦成像[20].其计算式为

2 球面阵列被动三维成像讨论

在理想情况下，若要对观测目标进行三维成像，需要从三维空间的各个角度方向对目标的电磁辐射信号进行测量.因此，一个能够包围目标且阵元在球面上均匀分布的球面阵列是一个理想的成像阵列.图5 所示为本文利用斐波那契网格[21]生成的球面半径为1.5 m、阵元数量为500 时的均匀球面阵列.宏观上看：球面上阵元密度在各处基本相等，阵元均匀分布在球面上.

图5 均匀球面阵列Fig.5 Uniform spherical array

2.1 阵元数量与成像性能

本节将通过对成像系统点扩散函数(point spread function,PSF)的仿真分析，对球面阵列中阵元数量对成像性能的影响进行评估.

选取直径为3 m 的球面阵列对理想点辐射源进行成像仿真.由于被动人体安检三维成像的理论分辨率约为半个工作波长，因此为实现厘米级甚至毫米级的图像分辨率，一般选取毫米波波段的人体辐射信号进行成像.考虑到三维成像计算量较大的因素，选取较低的工作频率(20 GHz)开展仿真计算，阵元数量分别选取100、1 000、10 000 进行对比.将理想点辐射源置于球面阵列中心位置，观测PSF沿X、Y、Z轴三个方向的强度分布，评估该成像系统在每个方向上的空间分辨率和动态范围.图6 所示为阵元数量分别为100、1 000 以及10 000 时的PSF 计算结果.可以看出：随着阵元数量由100 增加到1 000、10 000，PSF 的3 dB 波束宽度、第一旁瓣高度基本趋于一致，即X、Y、Z三个方向的PSF 主波束基本重合，且主波束的3 dB 波束宽度相等，因此该球面阵列在中心位置的成像结果在三个维度上具有相同的分辨率.

图6 不同阵元数量球面阵列的PSFFig.6 PSF of a spherical array with different numbers of elements

2.2 球面阵列内部不同位置的成像性能

为考察成像区域不同位置的成像性能，需要将理想点辐射源分别放置于观测目标区域的不同位置，计算各点的PSF 性能.本节对直径为3 m、阵元数量为500 的球面阵列内部不同位置的成像性能进行对比.考虑天线阵列的对称性，选取位于X轴上的A1(0.4,0,0)m、A2(0.6,0,0)m、A3(0.8,0,0)m三个点(如图7 所示)计算该点的PSF.

图7 理想点辐射源位置示意图Fig.7 Location of the ideal point source

图8 所示为点A1、A2、A3处的PSF沿X、Y、Z三个方向上的截线.可以看出，在不同位置的3 dB 波束宽度、第一旁瓣高度基本相同.因此当阵元数量固定时，理想均匀球面阵列所包含的成像区域在不同位置基本具有相同的成像分辨率和动态范围.

图8 不同方向上PSF 归一化强度分布Fig.8 The normalized intensity distribution of PSF on each dimension

2.3 成像分辨率

图9 所示为利用Sparrow 准则[22]对成像分辨率进行评估的仿真结果.可以看出：当两辐射源间距为7 mm( λ/2)时，两点源开始可分辨；当点源间距达到10 mm( 2λ/3)时，两点中心位置的强度小于 0.5，此时两点源完全可分辨.

图9 不同辐射源间距下利用Sparrow 准则计算的空间分辨率Fig.9 Spatial resolution calculated by Sparrow criterion with different spacing of radiation sources

2.4 成像遮挡对成像效果的影响

在实际的成像应用中，构成观测目标的点源辐射信号可能会受到其他辐射源的遮挡效应(blocking effect)使得其辐射信号无法被所有接收天线所接收.针对这一问题，本节将建立简单的成像遮挡模型，研究当存在遮挡影响时，成像结果的恶化程度.

假设位于球面阵列中不同位置的理想点辐射源其辐射信号仅能够被沿原点指向点辐射源位置方向上半球空间的天线单元所接收，天线阵列覆盖点辐射源周围 4π空 间的观测立体角始终保持 Ω=2π.将点辐射源位置沿X轴正半轴方向移动，随着点辐射源位置偏离球面阵列中心，阵列中能够有效接收点源辐射信号的天线数量逐渐减少，如图10 所示.

图10 观测立体角不变时不同位置点辐射源对应的有效接收天线示意图Fig.10 Schematic diagram of effective receiving antennas at different position of radiation sources with fixed observation solid angle

假设当点辐射源位于球面阵列中心时，仅有+X轴方向半个空间内的天线阵元能够接收到点辐射源辐射的信号(图11(a))，此时有效成像天线数量仅为原来整个球面阵列天线的一半，PSF 如图11(b)所示.将点辐射源沿+X轴方向移动，有效天线区域及PSF 如图11(c)、11(d)所示.可以看出：与阵列满阵时相比，X方向上的PSF 主波束有明显展宽，而Y、Z方向上的PSF 主波束宽度变化不大.说明考虑遮挡效果时，在本节假设的遮挡模型下，X方向的空间分辨率较Y、Z方向相比产生了明显下降.对比图11(b)、(d)可以看出，两种情况下X、Y、Z三个方向的PSF 并无较明显的差异.

图11 固定观测立体角时遮挡对成像性能的影响Fig.11 The impact of blocking on the imaging with fixed observation solid angle

表1 给出了当观测立体角不变时不同位置处的有效接收天线数量和PSF 性能的计算结果.可以看出，虽然在不同位置假设可接收到信号有效天线的数量逐渐减少，但由于接收天线始终能够对点辐射源周围的 2π立 体角空间(4π空间的一半)进行采样，因此对PSF 的3 dB 波束宽度和第一旁瓣高度均没有明显影响.

表1 观测立体角不变时不同位置处的有效接收天线数量和PSF 性能Tab.1 The number of effective receiving antennas and the PSF performance at different positions with fixed observation solid angle

当有效接收天线仅可对点辐射源周围有限立体角空间的辐射信号进行观测时，PSF 的3 dB 波束宽度和第一旁瓣高度的变化情况如图12 所示.将理想点辐射源置于球面阵列中心，改变有效接收天线所对应的空间立体角 Ω的值，计算此时的PSF.

图12 观测立体角改变时位于球面阵列中心的点辐射源对应的有效接收天线示意图Fig.12 Schematic diagram of an effective receiving antennas at array center with variable observation solid angle

图13 所示为观测立体角分别为1 .7π 和1 .2π时的PSF 计算结果.可以看出，随着观测立体角的减小，(d)中X轴方向3 dB 波束宽度与(b)中相比有了明显展宽.

图13 观测立体角不同时遮挡对成像性能的影响Fig.13 The impact of blocking on the imaging with different observation solid angle

表2 详细展示了不同观测立体角下的有效天线阵元数量和PSF 性能的仿真计算结果.可以看出，随着观测立体角的减小，三个方向的成像分辨率均有不同程度的恶化，其中沿X轴方向的分辨率恶化更加严重；但在动态范围方面，由于Y、Z方向PSF 的第一旁瓣有轻微下降，因此随着观测立体角的减小，在Y、Z方向获得了更大的动态范围.

表2 观测立体角变化时的有效接收天线数量和PSF 性能Tab.2 The number of effective receiving antennas and the PSF performance with different observation solid angle

总体来说，由于遮挡效果引起的观测立体角的减小会导致成像分辨率的下降.

2.5 对简单目标的三维成像

图14 和图15 分别展示了利用前述的球面阵列对一个二维圆环和一个三维长方体模型进行被动三维成像的仿真结果.为便于观测，选取了重构三维图像中归一化强度为0.9 的等值面作为最终的三维重构图像进行展示.

图14 二维圆环模型的三维成像结果Fig.14 3D imaging results of a 2-D ring model

图15 长方体模型的三维成像结果Fig.15 3D imaging results of a cuboid model

由仿真结果可以看出，被动毫米波三维成像能够很好恢复出被测目标的外形轮廓信息，进一步证明了被动三维成像的可能性.

3 通道型成像阵列的成像性能

球面阵列并不适用于实际的人体安检被动三维成像应用.为实现非合作式人体安检，需要设计通道型的三维成像阵列，以便被检人员在正常通行过程中完成安全检查.

为满足人体安检需求，本节分别选取三种不同长度的“门”型通道阵列对其成像性能进行分析.阵列1、2、3 的外形尺寸分别为1 m×1.5 m×2.5 m、1.5 m×1.5 m×2.5 m 和2.5 m×1.5 m×2.5 m；三种阵列的阵元排布均采取均匀排布方式，阵元间隔约为1 0λ；阵元数量分别为1 404、2 268、3 564.图16 所示为三种阵列的阵元分布情况以及当点辐射源位于阵列中心(即坐标原点)时的PSF.

图16 不同 “门”型通道阵列(左)及其中心位置处的PSF(右)Fig.16 Schematic diagram of the different portal array (left)with and its center position PSF (right)

选取如图17 所示的被动人体三维成像的几个典型位置，通过对这些位置的PSF 进行仿真分析，评估三种长度的“门”型通道阵列成像能力.

图17 “门”型通道阵列示意图Fig.17 Schematic diagram of the portal array

表3～5 分别为三种不同阵元数量的阵列对人体进行三维成像时，在图17 中所示的人体不同部位处的PSF 性能的仿真计算结果.

表3 1 404 阵元“门”型通道阵列的PSF 性能Tab.3 PSF performance of 1 404-elements portal array

表4 2 268 阵元“门”型通道阵列的PSF 性能Tab.4 PSF performance of 2 268-elements portal array

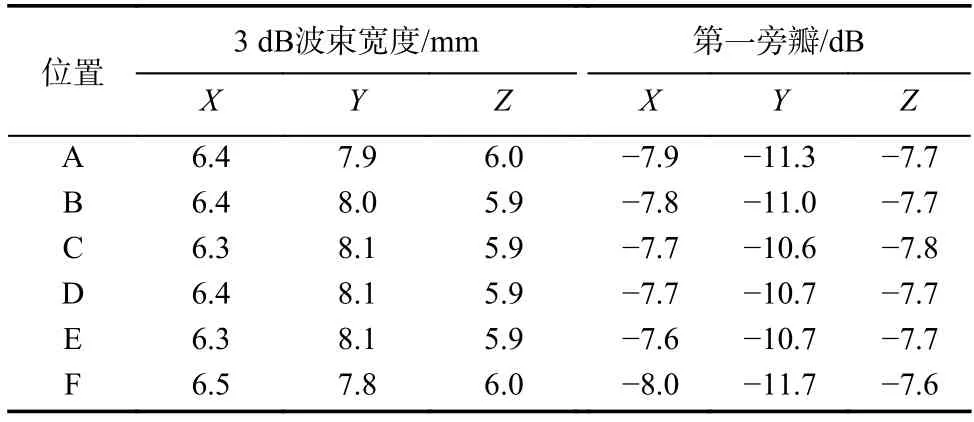
表5 3 564 阵元“门”型通道阵列的PSF 性能Tab.5 PSF performance of 3 564-elements portal array

根据上述仿真结果可以看出：与球面阵列相比，由于“门”型通道阵列两侧开口的存在，天线包围辐射源的空间立体角范围变小，导致成像分辨率以及成像动态范围的恶化.阵列在Y轴方向的边长较短，沿被检人员通行方向的成像分辨率恶化情况比其他两个方向更严重，通过增加通道长度(Y方向长度)可以有效提升成像分辨，且PSF沿X轴和Z轴方向的旁瓣性能比Y轴方向更差，因此沿X轴和Z轴方向的成像动态范围更小.

“门”型阵列是目前提出的一种在实际应用中较为可行的三维成像的安检通道阵列形式.本节仅对其在理想情况下的成像性能进行了初步分析讨论，对成像阵列不同位置的成像性能进行了初步的仿真计算，但其成像效果还受到工作频率、阵元分布、天线单元性能、成像算法等的影响，因此还需要进行更加深入细致的研究.就其在实际应用中的可行性而言，大规模天线阵列及大规模数字相关器阵列的设计也是其具体实现所面临的巨大挑战.一方面需要在保证成像性能的前提下尽可能降低硬件成本，这就要求要使用尽可能少的天线单元以及相关器.由于通道尺寸较大，且需要工作在毫米波频段，因此成本和功耗的控制至关重要.另一方面，为实现非合作式的人体安检，通道阵列需要在不影响被检人员正常通行的前提下，快速处理海量的测量信息并实时得到被检人员的三维成像结果，因此对于快速高精度的被动三维成像算法的设计也是其实现所面临的巨大难点.此外，大规模相关辐射计阵列的安装、校准、维护等问题也是潜在的难点.

4 总结与展望

被动毫米波三维成像是提升被动人体安检可靠性、实现非合作式人体安检的高效解决方案.本文主要针对被动毫米波三维成像系统的成像阵列对三维成像效果的影响开展初步分析，讨论了均匀球面阵列的三维成像效果以及不同尺寸的“门”型通道阵列的成像性能，为被动三维成像系统的实现提供了理论依据.被动毫米波三维成像系统的实现仍然面临诸多现实问题，快速高精度的反演成像算法、稀疏三维成像阵列布局设计、高性能低成本的系统硬件实现等，将会是今后研究的重点、难点所在.