前视成像中Keystone 变换残余距离走动的频域补偿

李泽森 李悦丽 张金福

（国防科技大学电子科学学院,长沙 410073）

引 言

雷达具有全天候、全天时、远距离的目标探测和定位能力，前视成像是指在飞行过程中雷达天线对前视方向进行扇形扫描并结合超分辨或单脉冲测角技术来提高前视方向的方位分辨率[1-2]，具有系统复杂度低、对航迹无特殊要求、方位分辨率改善显著等优点.

对空载雷达前视成像而言，平台高速运动会导致目标积累时间内出现严重的距离走动现象，影响图像聚焦性能，因此需要对目标跨距离单元走动进行校正.Keystone 变换是一种有效校正目标线性距离走动的方法，最早由Perry 等人提出[3]并应用于合成孔径雷达[4-6]，张顺生等人将Keystone 变换引入到雷达微弱目标的长时间积累领域[7]，也取得了良好的积累效果.Keystone 变换具有以下优势：1)可同时对多个目标进行线性距离走动补偿；2)保留了目标回波的相位信息，便于实现相参积累；3)在较低信噪比时依旧适用.Keystone 变换因其优越的性能，又被广泛应用于运动平台前视成像中[8-10].

雷达脉冲重复频率(pulse repetition frequency,PRF)限定了可观测到的最高多普勒频率，当运动平台速度较高或者雷达采用低PRF 时，将发生多普勒模糊，此时直接观测得到的多普勒谱的峰值频率点不再为多普勒中心的真实值，必须进行解多普勒模糊[11].常用的解多普勒模糊方法有一维集算法、中国余数定理法等[12].相关研究对多普勒模糊数的影响进行了分析[13-14]，但没有考虑模糊数与真实多普勒中心误差的影响.在运动平台前视成像模型中，平台飞行速度属于先验信息，易获得多普勒模糊数，但在解多普勒模糊时，采用Keystone 变换校正的模糊数补偿可能引入速度残差，导致目标定位误差.现有解决方法通常选取平台飞行速度对应的特定PRF，尽可能降低引入的速度残差[10,15]，但并未深入讨论解模糊所导致的速度残差问题.

本文首先研究了在多普勒模糊的情况下，基于Keystone 变换进行前视成像距离走动校正可能产生的速度残差问题，推导提出一种频域补偿Keystone变换残余距离走动的方法.该方法可以消除Keystone变换所产生的速度残差，通过理论分析与仿真实验验证了所提出方法的有效性.

1 前视成像距离走动误差影响分析和补偿方法

1.1 运动平台前视成像几何模型

前视高分辨成像通常是指雷达对前视方向采用扫描模式进行连续扫描，然后通过沿距离门的超分辨或单脉冲测角技术改善前视实孔径雷达图像方位分辨率的方法[2,10].

但是，由于雷达平台的运动，目标在回波距离门上的位置会发生变化，如图1 所示.机载雷达以匀速v从A点飞到B点的过程中，目标点P相对雷达的瞬时斜距为

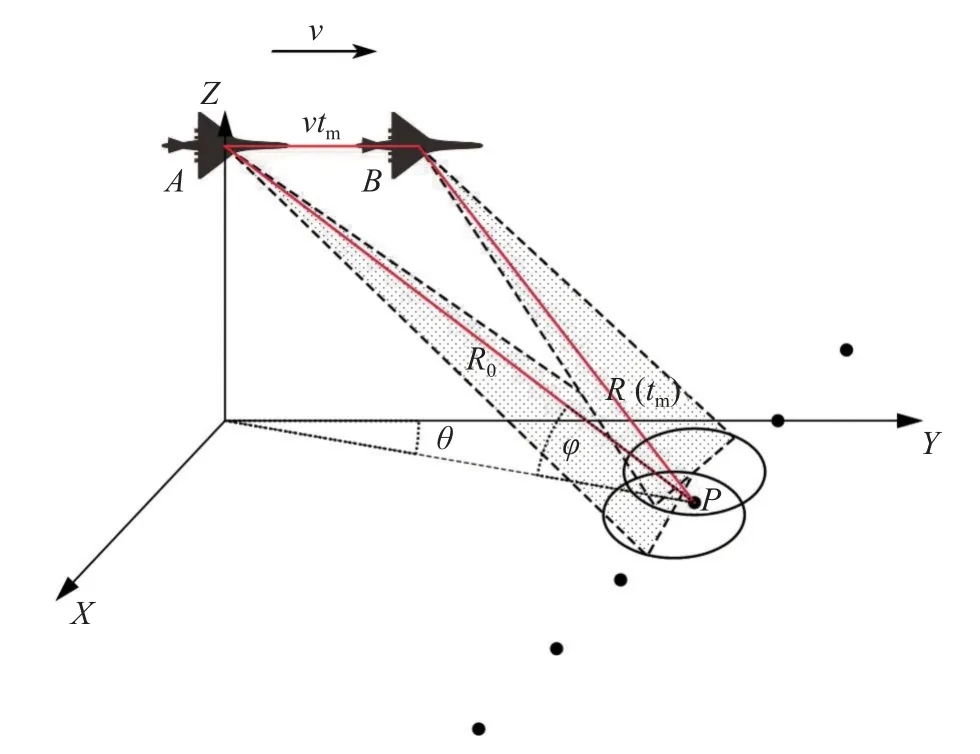
图1 运动平台前视成像几何关系模型Fig.1 Geometric model for forward-looking imaging of moving platforms

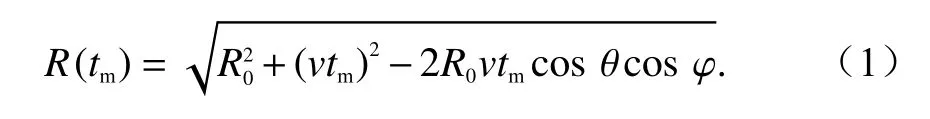
式中：R0为A点雷达平台到目标P的瞬时斜距；tm为慢时间；θ为目标相对飞行轨迹所在坐标轴Y轴的斜视角；φ为雷达对目标的俯视角.对式(1)进行泰勒级数展开，可以得到

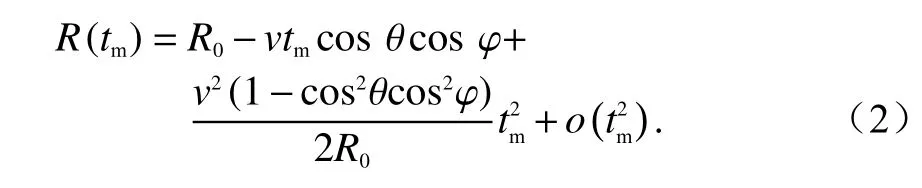
在雷达天线波束扫描过程中，由于平台的前向飞行速度，回波中目标相对天线相位中心的距离会发生变化，式(2)中第2 项表示由前向飞行速度引起的线性项，称为距离走动，其值与 θ 和φ均有关.在远场成像时φ的变化相对较小，可以认为φ角相对固定，忽略其变化.在天线扫描成像的过程中，不同方位相同距离的目标回波会在同一时刻到达，但是它们在不同帧之间的距离走动各不相同，使得无法进行统一的校正.对这种空变距离走动进行补偿的方法有两种：频域距离走动校正或Keystone 校正.

1.2 频域距离走动校正

假设雷达发射线性调频脉冲信号，雷达发射信号的时域表达式为

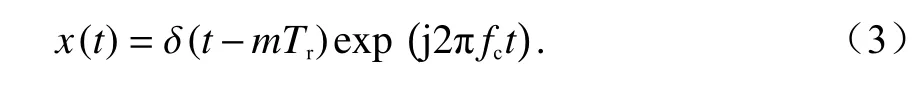
式中：δ(t)为 chirp 脉冲；m为脉冲序列；Tr为脉冲重复时间；fc为载波中心频率.

雷达接收到距离压缩后的时域回波可以表示为

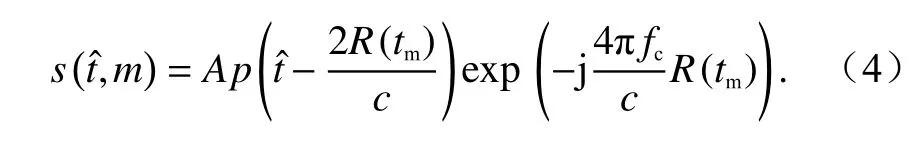
式中：A为点目标的回波强度；p(·)为归一化的回波包络；=t-tm为快时间；tm=mTr.将式(4)沿快时间维tˆ做傅里叶变换，得到回波在距离频域表达式为

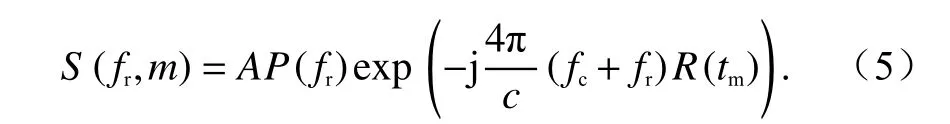
式中：P(fr)为p()的傅里叶变换；fr为快时间tˆ的频域.

式(2)中 θ角的变化范围为前视方向目标区域成像角度范围，通常小于15°，对应余弦值变化很小，因此在距离走动校正时可以忽略不同 θ角目标的距离走动差异，统一用正前方目标的距离走动曲线进行校正，此时式(2)可化简为

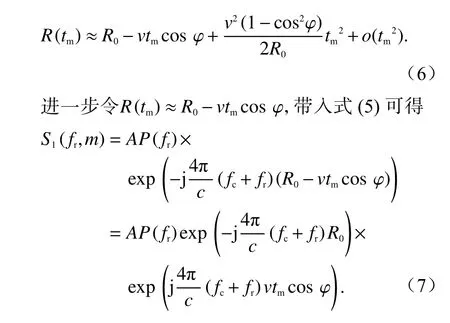
式(7)中，指数项第二部分表明距离频率与多普勒频率之间存在耦合关系，文献[16]中针对跨距离单元走动提出了一种频域距离走动校正方法，该方法通过共轭消除距离频率与多普勒频率之间的耦合.

采用频域距离走动校正的方法对式(5)中的回波包络进行校正，消除距离频率与多普勒频率的耦合项，可以得到

由式(9)可以发现，频域距离走动校正方法将会引入残余包络误差 ΔR(tm)：

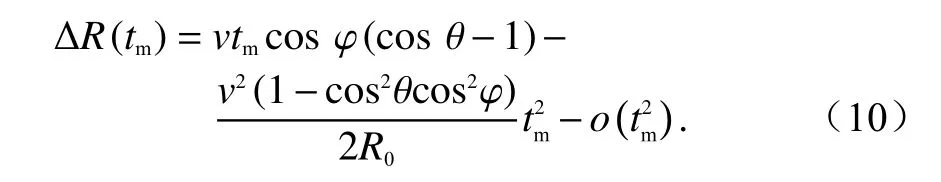
前视成像区域内 θ角较小，ΔR(tm)主要由第一项组成，且在速度较小时，式(10)中第一项接近于零，此时残余包络误差可以忽略.但是当速度较大时，残余包络误差急剧增大，所以此时采用频域距离走动校正方法时将会引入较大误差.为解决这一问题，前视成像通常采用Keystone 变换进行距离走动校正.

1.3 Keystone 校正方法和问题分析

令R(tm)=R0-vtmcos θcosφ，带入式(5)中得

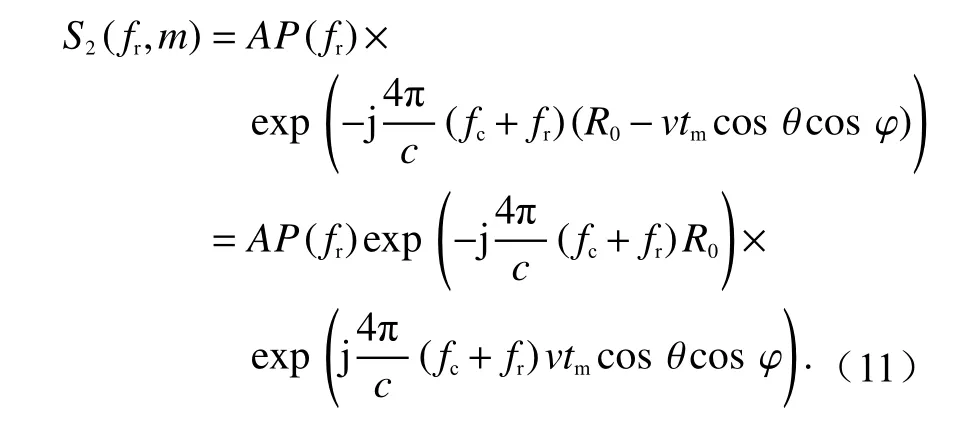
为消除距离频率与多普勒频率之间的耦合，对慢时间进行尺度伸缩变换，令

即Keystone 变换[3]，得到

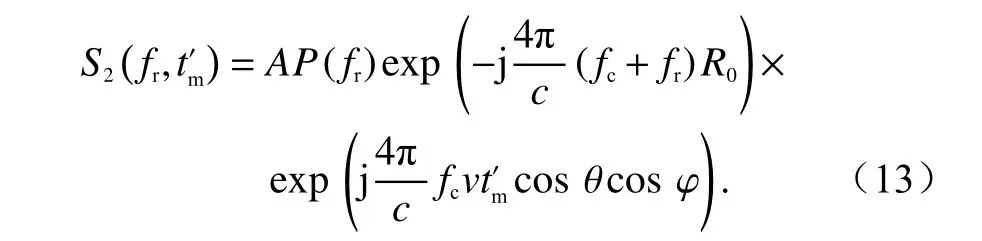
Keystone 变换消除了距离频率与多普勒频率之间的耦合，补偿了目标的线性走动.对高波段雷达，通常满足fr≪fc，式(13)满足fc/(fc+fr)≈1，且指数项第二项与距离频率无关.对式(13)进行傅里叶反变换得到

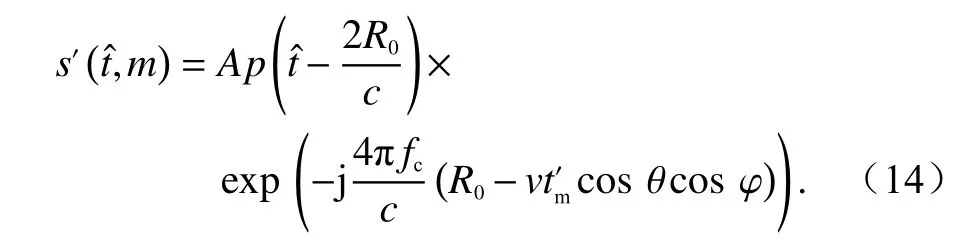
由式(14)可以看出，经过Keystone 变换距离走动校正后，目标在不同方位的位置均为R0，说明Keystone变换消除了距离频率与多普勒频率之间的耦合，补偿了目标的距离走动.

实际上，雷达是以慢时间tm进行采样的，fc/(fc+fr)×时刻并没有实际的采样值，通常需要采用sinc 内插算法实现Keystone 变换[17].

对于高波段雷达，由于PRF 小于多普勒中心频率往往引起多普勒模糊问题，所以在进行sinc 插值的同时还应进行解多普勒模糊相位修正.在多普勒模糊的情况下，Keystone 变换实现方法[18]可以表示为

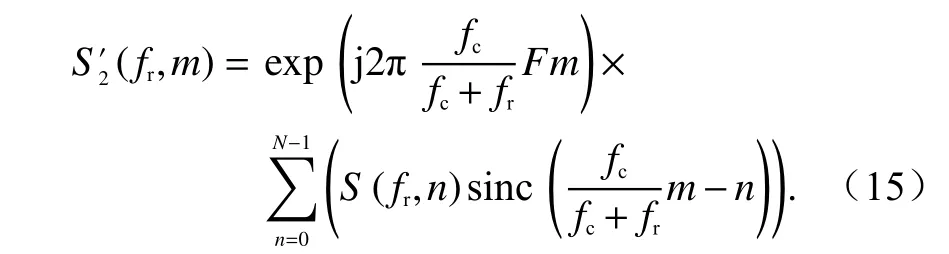
式中：F为多普勒模糊倍数；N为相参积累时间内脉冲个数.

由式(15)可以看出，对模糊数的依赖是Keystone算法的一个限制条件[7]，定义模糊数F为

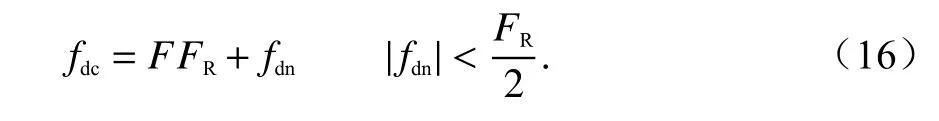
式中：FR表示PRF；fdc表示多普勒中心频率，

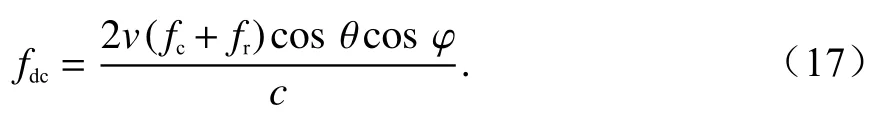
发生多普勒模糊时实际测得的多普勒中心频率为fdn，fdw为多普勒带宽，且有

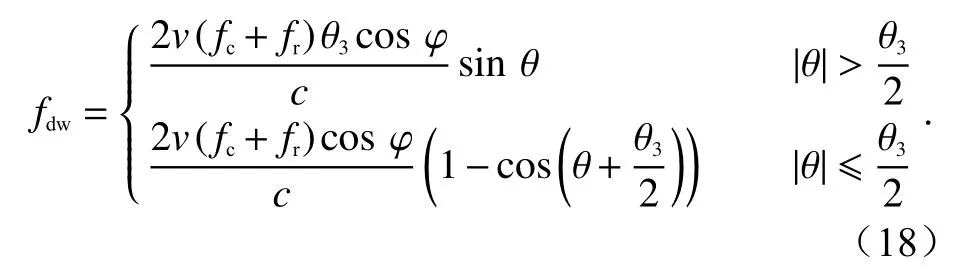
式中，θ3为3 dB 波束宽度.

图2 为前视扫描雷达解多普勒模糊产生速度残差示意图.当斜视角θ=0°、频率为fc时，雷达回波的多普勒中心频率为

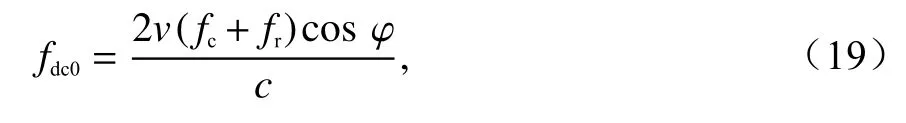
天线主瓣内回波的多普勒带宽为

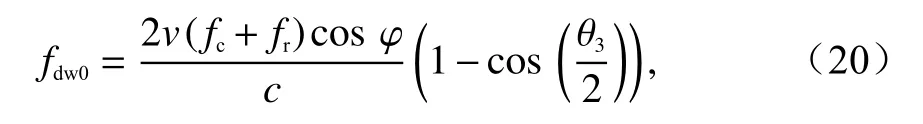
发生多普勒模糊时测得的多普勒中心频率为fdn0，多普勒模糊数对应的多普勒中心频率为

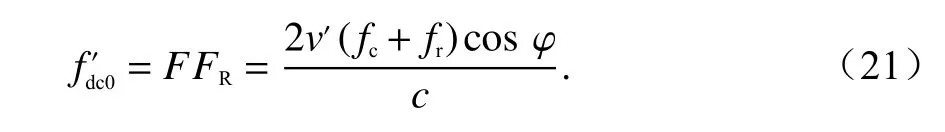
式中：v′=v+Δv为对应的速度，Δv为模糊数补偿后相比于真实速度引入的速度残差，

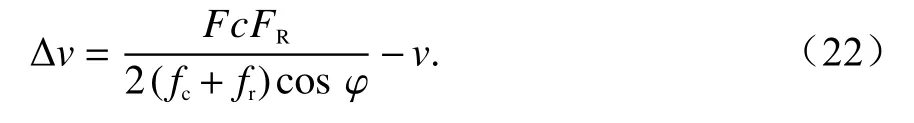
当斜视角 θ ≠0 °、频率为fc时，所对应的多普勒中心频率、多普勒带宽、发生多普勒模糊时测得的多普勒中心频率以及多普勒模糊数对应的多普勒中心分别为fdcθ、fdwθ、fdnθ、.由图2 可见，当雷达斜视角增大时，多普勒中心频率偏移减小，多普勒带宽增大.因此在正前视方向，利用多普勒带宽区分目标非常困难，同样由于飞行方向左右两侧的斜视角都会引起相同多普勒中心偏移，多普勒波束锐化技术存在左右模糊问题.

当fdn0≠0时，因为多普勒模糊数F为整数，用式(15)解多普勒模糊将产生模糊数误差，且有

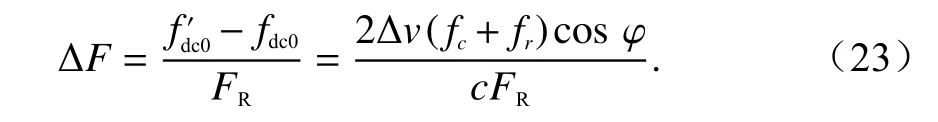
如图2 所示.

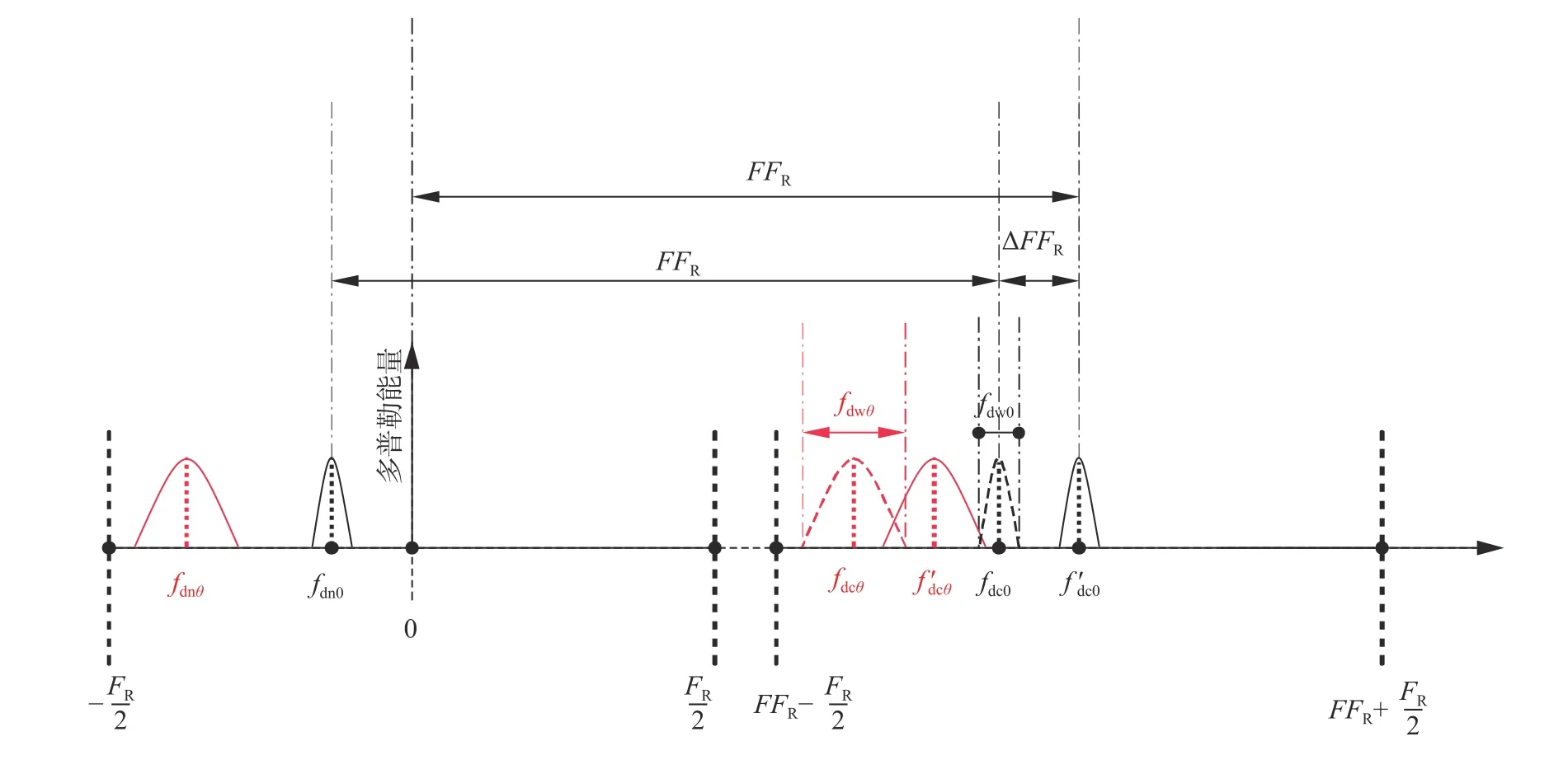
图2 解多普勒模糊产生速度残差示意图Fig.2 Schematic diagram of the residual velocity generated by solving Doppler ambiguity

相关研究对多普勒模糊数的影响进行了分析[13-14]，但未考虑模糊数误差的影响，多普勒模糊情况下所产生的残余距离走动校正误差是由于解多普勒模糊时产生了速度残差.针对产生的速度残差进行分析，在未发生多普勒模糊时，式(11)中存在距离频率与多普勒频率耦合的相位项为

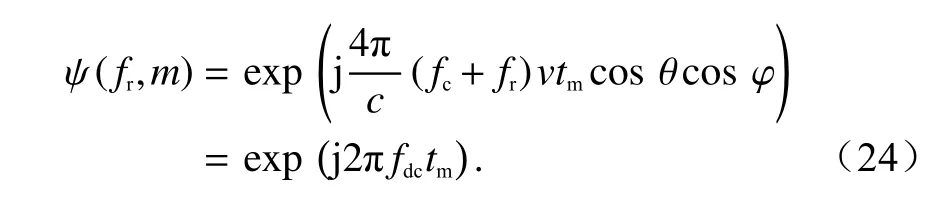
解多普勒模糊后，相位项变为

式(27)说明，经过Keystone 变换校正后，如果模糊数对应的多普勒中心频率与实际多普勒中心频率不同，则会引入速度残差 Δv，将影响最终的目标定位结果.

2 频域补偿Keystone 变换残余距离走动校正的方法

根据前文的分析，单纯采用平台飞行方向的速度作为参考速度进行频域距离走动校正，会导致与角度相关的残余包络误差，且这一误差随扫描角度增大而增大，在高速平台上尤其明显；而采用Keystone变换校正时，由于存在多普勒模糊，解多普勒模糊时可能会产生速度残差，也会导致空变的目标定位误差.本节提出一种频域补偿Keystone 变换残余距离走动的方法，可以消除解多普勒模糊相位修正时所产生的速度残差，实现目标距离向准确定位.

存在多普勒模糊的情况下，由式(11)与式(27)可以得到经过Keystone 变换后的回波频域为

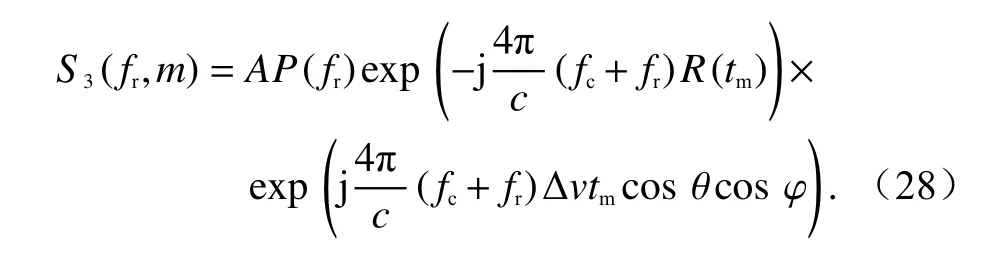
虽然距离频率与多普勒频率的耦合经过Keystone变换后得到消除，但引入了第二个指数项中距离频率与速度残差的耦合.

采用1.2 节中的频域距离走动校正方法，对式(28)中的速度残差进行校正：

Keystone 变换的结果经过频域距离走动校正，消除了速度残差与距离频率之间的耦合.同时相比于直接用频域距离走动校正方法，此时的速度残差Δv远小于平台飞行速度v，残余包络误差 ΔR′(tm)为

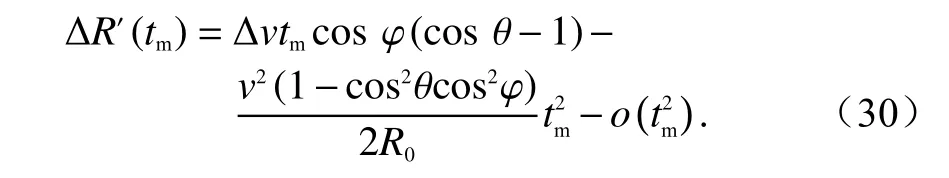
对比式(10)，频域补偿时所引入的残余包络误差大大降低.

经过上述处理，最终频域补偿Keystone 变换距离走动校正方法可表示为

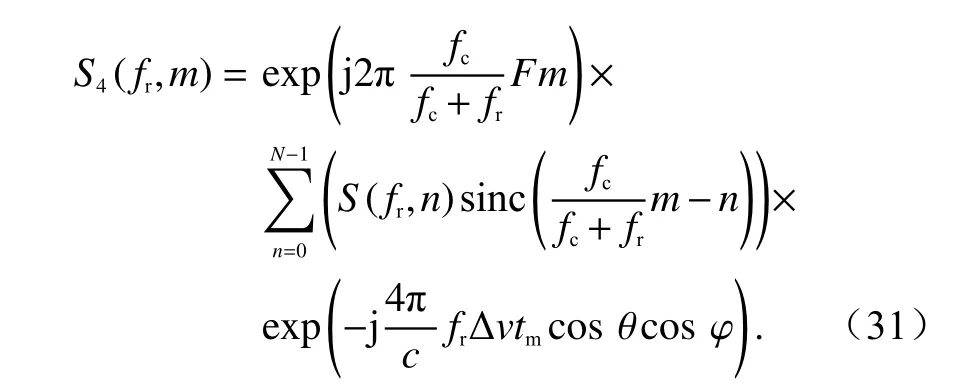
频域补偿Keystone 变换距离走动校正方法步骤如下：

1) 将距离压缩后的雷达回波沿快时间维进行傅里叶变换；

2) 对慢时间进行尺度伸缩变换消除距离频率与多普勒频率之间的耦合；

3) 存在多普勒模糊时进行相位修正解多普勒模糊，同时使用sinc 插值方法实现Keystone 变换；

4) 用频域距离走动校正方法补偿Keystone 变换所引入的速度残差.

3 仿真验证

3.1 点目标仿真实验

为验证所提方法，采用单脉冲前视成像算法进行仿真实验，仿真所用雷达系统参数如表1 所示.雷达放置在机载平台上，平台匀速飞行，发射信号中心频率fc为18 GHz，脉宽为1 μs，带宽为50 MHz.雷达扫描范围为-15°～15°，PRF=2 600 Hz，在地面上以[0，1 700] m 为中心设置3×21 点方阵，目标点的强度为1，点之间方位向、距离向间隔均为30 m.方位向测角采用调频Z变换重建和差多普勒估计并进行比幅测角的方法[15].

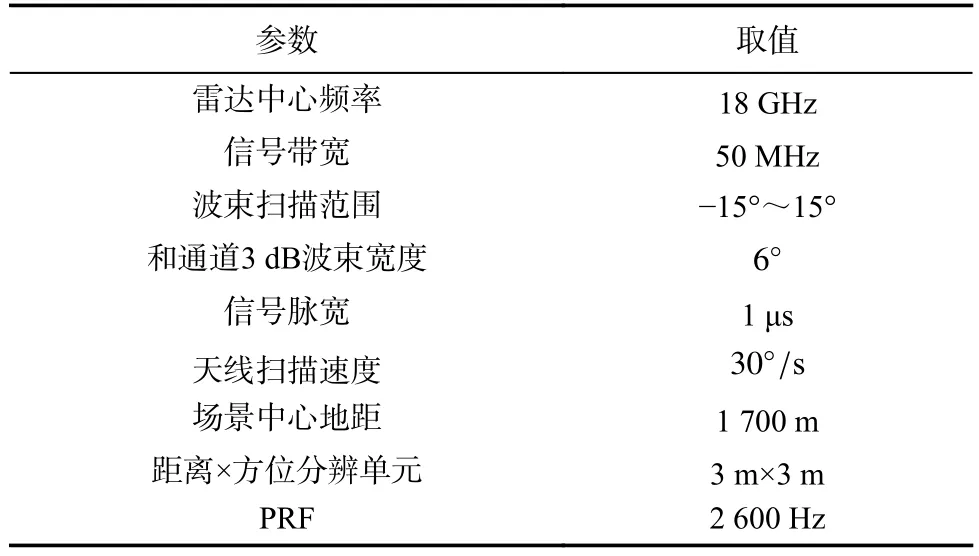
表1 前视扫描成像仿真实验参数Tab.1 Simulation experimental parameters for forwardlooking scanning imaging

当PRF=2 600 Hz时，设置不同的平台飞行速度v，分别求出fdc=2v fccosφ/c，多普勒模糊数(其中 〈·〉 表示四舍五入取整)，Δv=(ΔFcFR)/(2fccosφ)，具体参数取值如表2 所示.

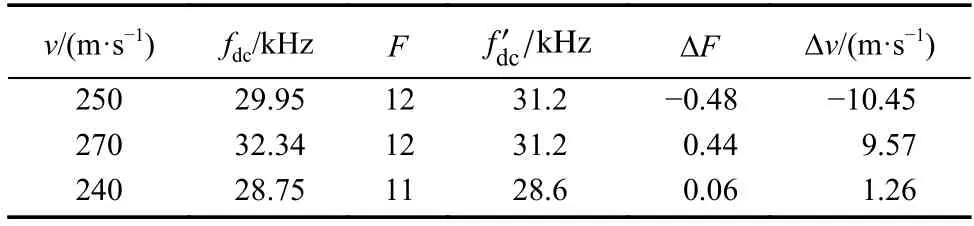
表2 平台不同飞行速度产生的速度残差Tab.2 Residual velocity by different speeds of the platform

图3 所示为平台不同飞行速度下传统Keystone变换校正结果与频域补偿Keystone 变换校正结果对比.图3 (a)、(b)、(c)所示为Keystone 变换方法校正结果，由于引入了速度残差 Δv，导致距离走动校正结果发生偏移. Δv越大，偏移越明显，Δv的正负导致了不同的偏移方向，Δv为正时产生顺时针偏移，Δv为负时产生逆时针偏移.图3 (d)、(e)、(f)所示为相同参数下采用频域补偿Keystone 变换校正结果，可见所提出的频域校正方法消除了速度残差引起的距离误差，实现了目标准确的距离向定位.

从图3 (a)与图3 (d)中分别截取方位向为-300 m的三个目标点绘制归一化剖面图，结果如图4 所示.三个目标点的真实距离分别为1 670 m、1 700 m、1 730 m.可以看出：传统Keystone 变换校正的三个目标点在距离向均产生了3 m 的偏移；而频域补偿Keystone 变换由于消除了速度残差引起的距离误差，实现了距离向的准确定位.

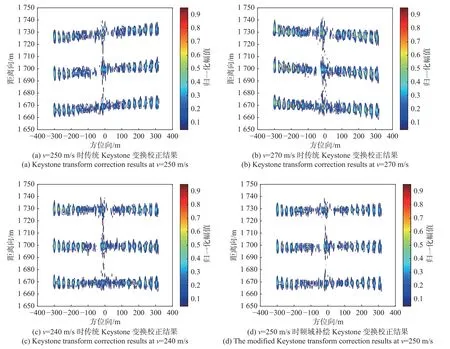
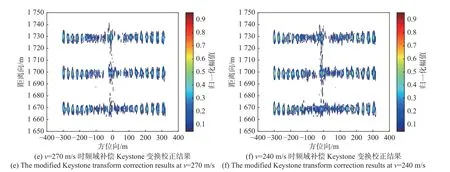
图3 传统Keystone 变换与频域补偿Keystone 变换校正结果对比Fig.3 Comparison of the correction results of Keystone transform and the modified Keystone transform

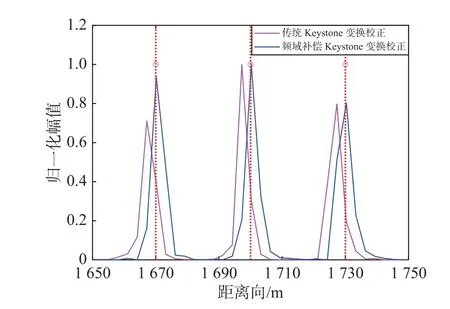
图4 v=250 m/s 时方位向-300 m 目标归一化剖面图Fig.4 Normalized profiles of the targets with an azimuth of-300 m,v=250 m/s

图5 所示为频域校正方法与频域补偿Keystone变换校正方法结果对比，设置平台飞行速度v=270 m/s.截取方位向分别为-300 m、-270 m、-240 m，距离向分别为1 670 m、1 700 m、1 730 m 的3×3 点方阵做等高线图.可以看出：在机载平台高速运动时，频域校正方法产生的残余包络误差较大，导致聚焦效果变差；而频域补偿Keystone 变换方法，仅用频域校正方法处理速度残差 Δv，产生的残余包络误差较小，具有更好的聚焦效果.

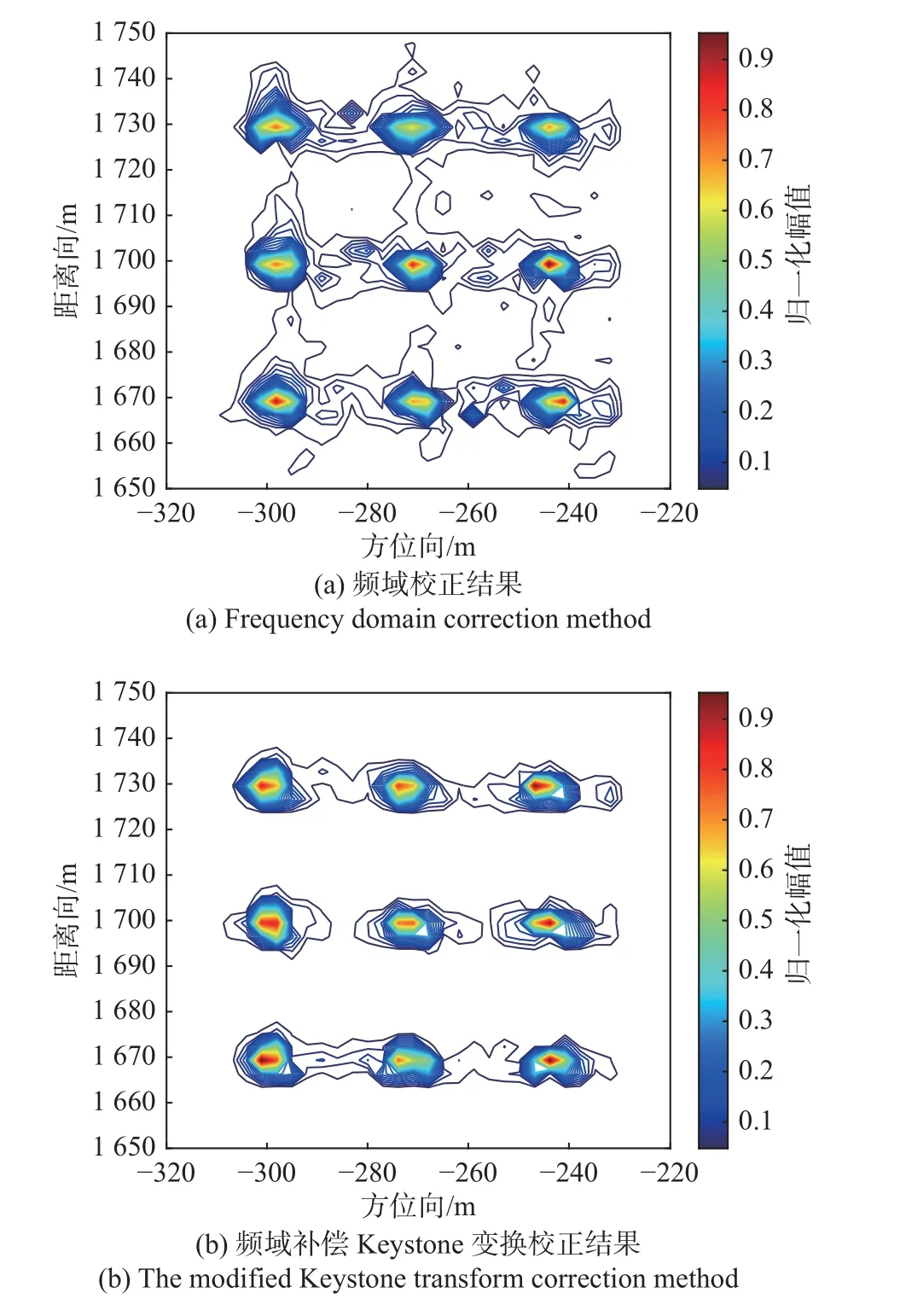
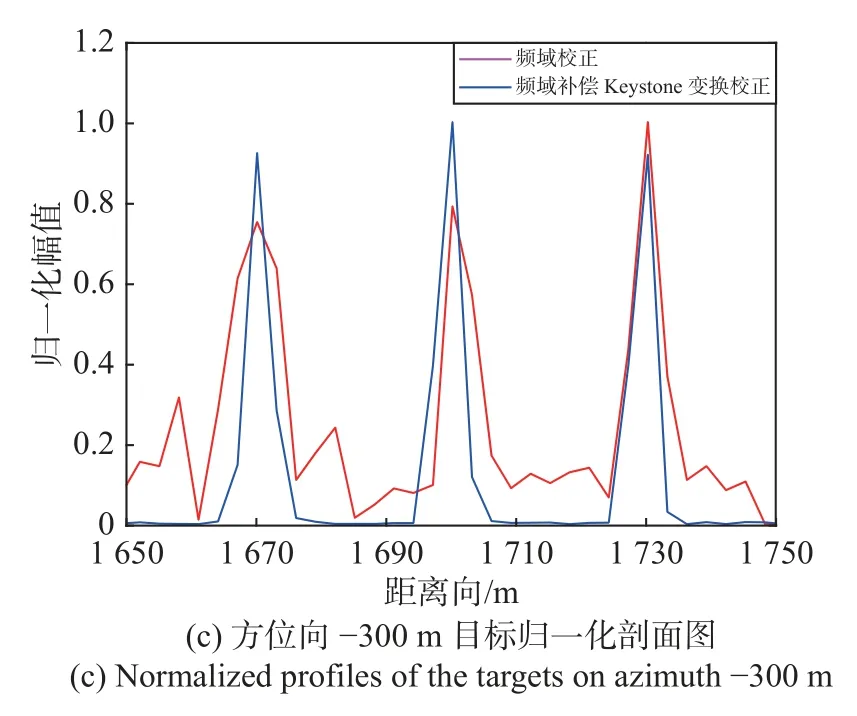
图5 频域校正方法与频域补偿Keystone变换校正方法结果对比Fig.5 Comparison of the correction results of frequency domain correction and the modified Keystone transform

为进一步证明所提算法的有效性，分别计算距离向1 700 m，方位向-300 m、-270 m、-240 m 处目标采用频域校正方法与频域补偿Keystone 变换校正方法校正结果5 倍插值后的距离向积分旁瓣比(integral sidelobe ratio,ISLR)，

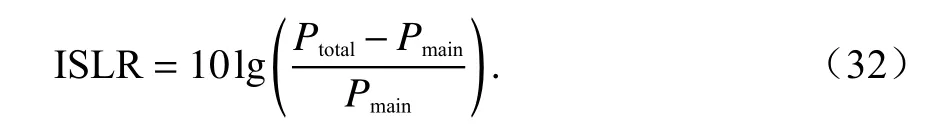
式中：Ptotal为总功率；Pmain为主瓣功率，主瓣宽度以峰值为中心，大小取两倍3 dB 带宽.两种方法距离向ISLR 结果如表3 所示，图6 所示为距离向1 700 m、方位向-300 m 的目标5 倍插值后的距离向剖面图.在同一方位向处，频域补偿Keystone 变换校正方法的距离向ISLR 均低于频域校正方法的距离向ISLR，说明频域补偿Keystone 变换校正方法能量更集中，聚焦效果更好.同时，频域校正方法的距离向ISLR 随着方位向的降低而减小，这是因为随着斜视角 θ的减小，式(10)所示的残余包络误差变小，聚焦效果变好.

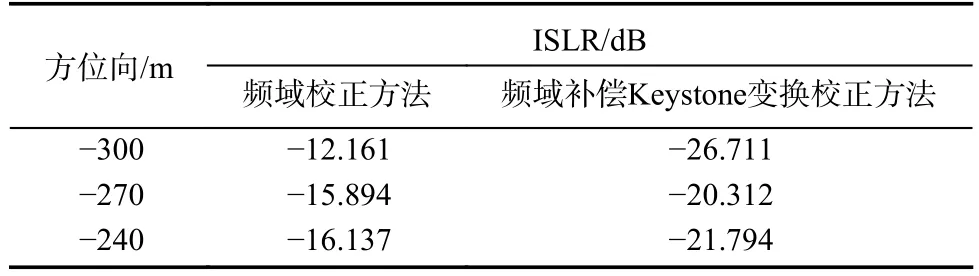
表3 频域校正方法与频域补偿Keystone 变换校正方法的距离向ISLR 对比Tab.3 ISLR comparison between frequency domain correction method and the modified Keystone transform

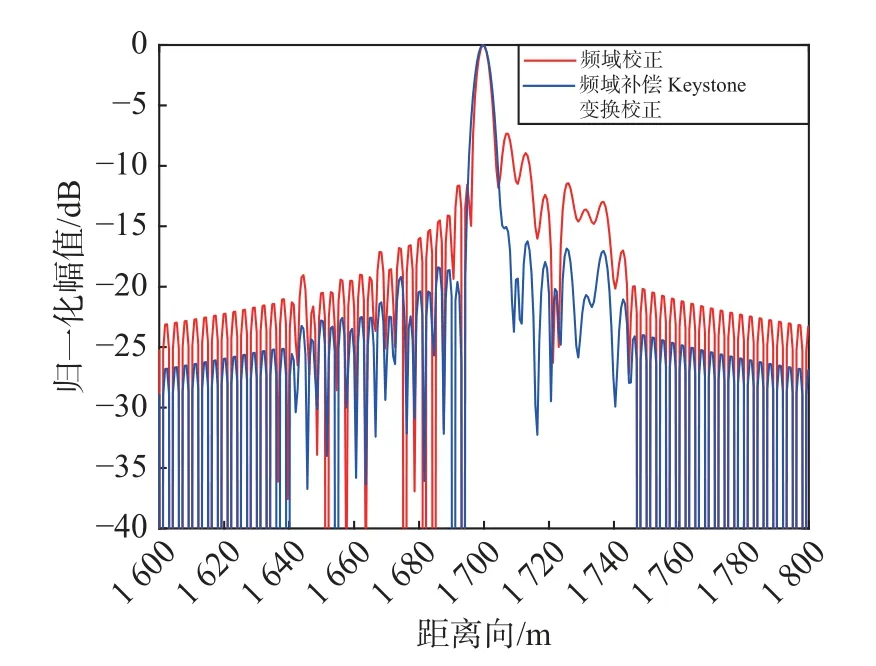
图6 距离向1 700 m、方位向-300 m 的目标距离向剖面图Fig.6 Target distance direction profiles with a distance of 1 700 m and azimuth of -300 m

3.2 场景仿真实验

点目标仿真实验验证了频域补偿Keystone 变换方法的有效性，接下来验证所提出方法用于重建扩展目标的可行性.仿真采用一幅Ku 波段的SAR 图像作为原始场景，对图像进行降采样处理，图像分辨率为3 m×3 m，如图7 (a)所示.图像数据置于以[0，1 700] m 为中心的地面，平台飞行速度为100 m/s，其余参数与表1 中相同，成像结果用dB 图表示.

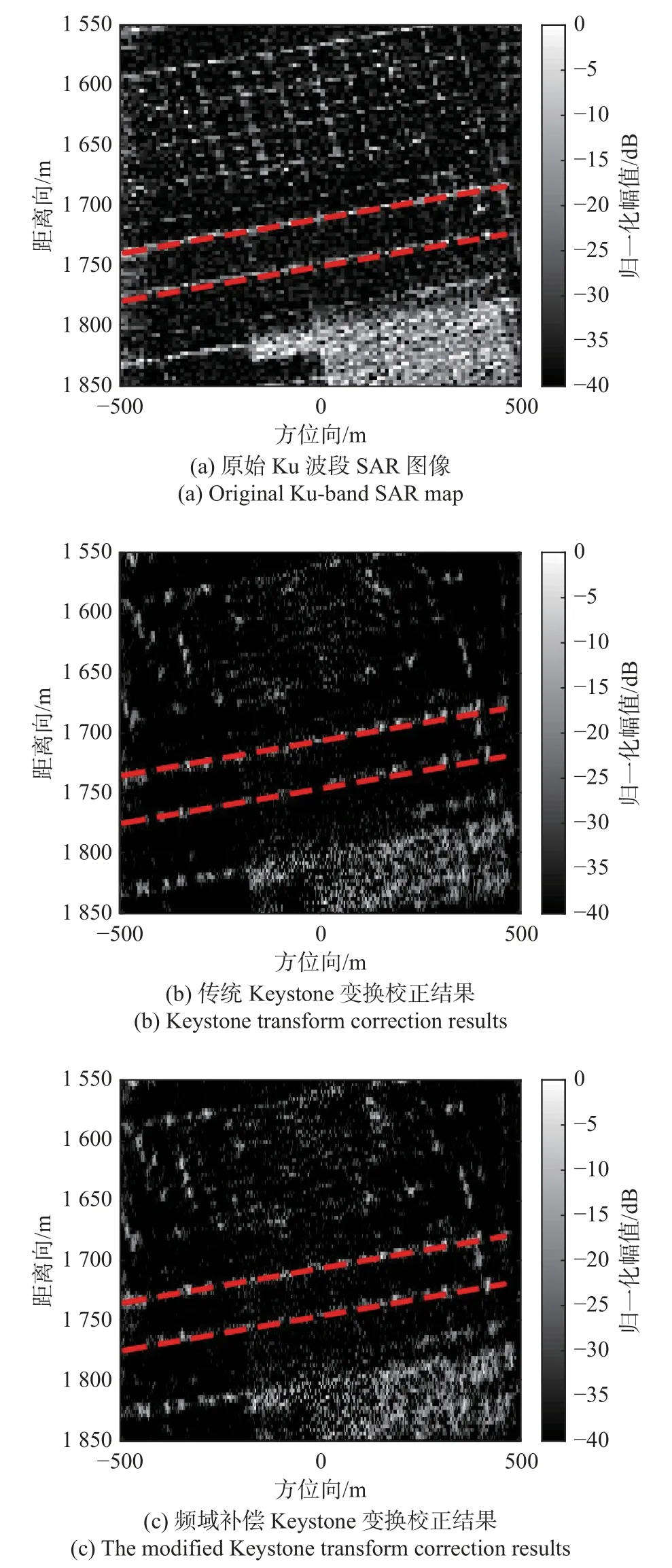
图7 仿真场景校正结果对比Fig.7 Comparison of correction results in simulation scenes

图7 (b)与图7 (c)分别为传统Keystone 变换方法与频域补偿Keystone 变换方法成像结果，红色虚线为目标真实场景位置.传统Keystone 变换方法校正结果产生了偏移而频域补偿Keystone 变换方法可以准确地重建目标场景.实验结果验证了频域补偿Keystone 变换方法重建扩展目标时的有效性.

4 结 论

机载运动平台雷达前视扫描成像时，由于运动平台速度较高，常会引起多普勒模糊.在进行距离走动校正时，使用传统Keystone 变换方法将引入速度残差，造成距离走动校正失准.现有解决方法通常选取特定的PRF 与平台飞行速度，尽可能降低引入的速度残差，但限制了系统选择的灵活性.本文首先分析了速度残差产生的原因，进一步提出了一种频域补偿Keystone 变换残余距离走动的方法，可适应不同的PRF 与平台运动速度，该方法可以消除Keystone 变换所引入的速度残差，实现目标距离向的准确定位，理论分析与仿真实验验证了该方法的有效性.如何消除二次包络误差，实现更好的聚焦效果，以及实现复杂机动情况下的距离走动校正，这将是我们下一步的研究方向.