基于深度迭代网络的穿墙雷达成像方法
王玉皞 张玥 周辉林 刘且根 蔡琦
(南昌大学信息工程学院,南昌 330031)
引 言
穿墙雷达成像(through-the-wall radar imaging,TWRI)是一种非接触和非破坏性电磁感知技术,由于电磁波具有穿透非金属建筑材料的能力,可实现墙后或封闭环境中隐蔽目标的探测、定位、跟踪以及成像,广泛应用于灾难救援、安防和城区巷战等民用和军事领域[1-3].在TWRI 中,由于墙体反射而产生的强杂波往往会淹没来自墙后或建筑物内静止目标的反射信号,影响成像精度和后续目标检测性能.目前为止已经有许多墙体杂波抑制方法被提出,如空间滤波[4]、子空间分解[5]和稀疏信号表示[6]等.但这些方法大部分采用两阶段策略,分别解决墙体杂波抑制和图像重建问题,其图像的重构质量完全取决于墙体杂波滤除的效果.
文献[7]提出了一种迭代优化方法,将雷达数据分解为对应杂波分量的低秩矩阵和对应目标分量的稀疏矩阵,然后采用迭代优化算法抑制墙体杂波并同时得到目标图像.与传统的两阶段TWRI 方法相比,该方法精简了TWRI 过程,并且更高效地抑制墙体杂波以及重构目标图像.进一步地,文献[8]在联合低秩和稀疏模型上引入了全变分正则化器,将原始全变分先验推广为联合微分稀疏的全变分正则化,以保证目标区域的连续性并有效抑制图像鬼影.然而,这些基于迭代的成像方法在模型建立和优化求解过程中对于各种正则化参数、阈值的选取没有具体公式指导,都是采用试错法选择最佳参数,且该参数与场景密切相关,存在计算代价高、对初值敏感及重构速度慢等问题.
近年来,深度神经网络由于具有从数据中学习特征的能力,在信号处理领域及图像视觉相关领域都取得了极大的突破.在雷达领域,深度学习也受到了广泛的关注.针对单通道步进频率连续波穿墙雷达,文献[9]引入了ResNet 深度卷积神经网络,解决封闭建筑空间中多个移动人体目标计数的问题.文献[10]从数据驱动的角度展开了相应的基于深度网络的探地雷达前向数值模拟研究,然而只是将深度网络作为给定输入及输出条件下数据驱动的函数逼近器,并没有研究更具有物理意义的求解框架.文献[11]提出一种去噪自编码器的深度网络,在不需要已知墙体参数和建筑物布局条件下,实现穿墙雷达的图像重建.文献[12]提出了一种基于全卷积网络的自适应目标检测方法,通过提取多尺度特征来实现TWRI 中弱散射目标成像.生成式对抗网络(generative adversarial nets,GAN)作为无监督学习的新兴方法,在TWRI 领域也体现了一定优势,通过生成器和鉴别器的相互博弈能够有效地抑制TWRI 中的多径鬼影[13-14].这些网络都为纯数据驱动,在杂波抑制和成像方法上相较于传统重建方法具有一定优势,但也存在依赖大数据集、训练时间长、泛化能力差等问题.文献[15]则提出了一种具有低秩投影的稀疏自编码器,通过解决增广拉格朗日乘数优化问题来确定网络的权重,能够有效抑制墙体杂波并恢复目标信号.
有别于上述纯数据驱动和物理模型约束的深度网络,本文提出一种物理模型驱动的深度迭代网络,实现穿墙雷达室内目标成像.该网络结合数据驱动与领域知识,将墙体杂波抑制以及目标图像重建问题表示为联合低秩与稀疏分解驱动的正则化优化问题,然后基于轮换迭代的求解策略将该问题分解为两个子问题,分别求解低秩分量及稀疏分量的子优化问题,并推导其更新公式,将传统迭代优化算法的每步优化求解过程映射到深度迭代网络结构中的每个阶段,形成融合物理模型驱动的可学习深度迭代网络求解框架.该方法无需手动调节算法参数和预先选择正则化函数,与传统迭代方法相比较,本文提出的深度学习方法在推理阶段,重构速度快的同时,能高效抑制墙体杂波并且精确重构墙体后方的目标图像.
1 联合低秩与稀疏分解的优化问题
本文采用冲击脉冲雷达体制进行目标探测,雷达系统的收发一体天线阵列平行于墙体放置,收发一体天线阵元自左向右均匀步进前进,TWRI 系统探测示意图如图1 所示.图1 中x轴方向表示方位向,y轴方向表示距离向,步进方向上的天线阵元移动位置数为M,在每个天线阵元位置上雷达系统收发的频率个数为N,则系统在第m(m=1,2,···,M)个天线阵元位置和第n(n=1,2,···,N)个频点测量到的雷达回波信号数据yn,m可以表示为
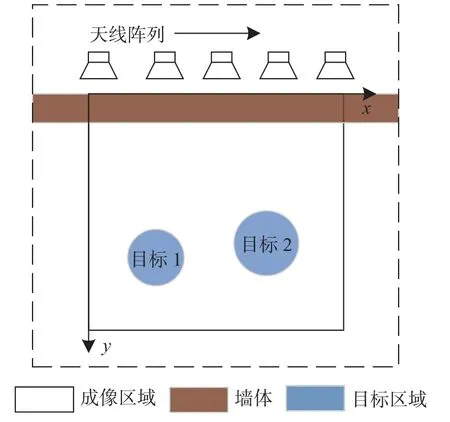
图1 TWRI 系统探测示意图Fig.1 TWRI system detection diagram


式中:σw为墙体的反射系数;fn为第n个工作频点;τw为第m个天线阵元位置和墙体之间的传输时延;P为探测场景中墙后的目标个数;σp为第p个目标的反射系数;τm,p为第m个天线阵元位置和第p个目标之间的传输时延.当天线沿水平方向均匀步进时,天线与墙体的距离保持不变,墙体回波仅与收发天线的相对位置有关,与其绝对位置无关[16].
为了进行图像重建,将待成像区域沿距离向和方位向划分成Q=I×J个均匀空间网格,其中I和J分别代表距离向和方位向的离散网格数,每个离散网格数都代表一个成像像素点.则待重建图像经过按列堆叠转换为Q×1维 场景反射系数向量s,其第q(q=1,2,···,Q)个 元素sq表示第p个目标占用的第q个像素点的反射系数 σp.
在每个天线阵元测量位置得到的N个工作频点的信号和vn,m可以分别堆叠成N×1维向量和vm. 其中,第m个天线阵元测量位置上的目标信号可以表示为

式中,Ψm为N×Q维矩阵,其第n行第q列的元素可以表示为

τm,q表示第m个天线阵元位置和第q个成像网格之间的传输时延.
图2 给出了电磁波在第m个天线位置和第q个成像网格之间的传播路径.Tx 表示发射机,Rx 表示接收机.lm,q,air2,t,lm,q,wall,t,lm,q,air1,t分别表示电磁波在发射天线和第q个成像网格之间经过各介质的距离;而lm,q,air2,r,lm,q,wall,r,lm,q,air1,r则分别表示电磁波在接收天线和第q个成像网格之间经过各介质的距离.因此,第m个天线阵元位置和第q个成像网格之间的传播时延 τm,q表示为[17]
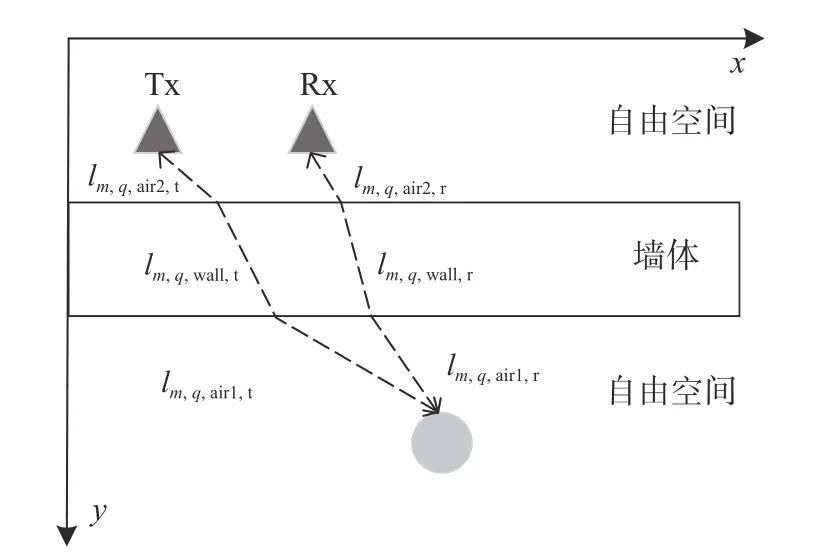
图2 电磁波传播路径Fig.2 Electromagnetic wave propagation path

式中:c为电磁波在自由空间的传播速度;v=为电磁波在墙体内的传播速度,εw为墙体的相对介电常数.
将M个天线阵元位置的目标信号进行堆叠可得到总的目标回波信号yt为

再将M个天线阵元位置的N×1维 向量ym、和vm堆叠成MN×1维向量,可得出式(1)的向量形式为

在穿墙雷达探测场景中墙体位置相对固定,每个天线位置上的墙杂波相关性较强,因此yw可认为是一个包含墙体回波信号的低秩分量.
基于压缩感知(compressive sensing,CS)理论[18],通过测量矩阵 Φ来表示压缩测量向量B和整个信号向量y之间的关系:

式中:Φ为K×MN维的测量矩阵,由从MN×MN的单位矩阵中随机选取K行组成.将式(7)代入式(8)可得:

式中:Ω=ΦΨ;n=Φv.因此,根据式(9)及各向量的特性,雷达探测目标图像重建问题可以通过建模一个低秩联合稀疏的最小化问题来求解:

式中:‖·‖为核范数,表示yw的奇异值和;‖·‖1,2为混合的l1,2范数,其值等于s每一行的l2范数和;λ1和λ2分别对应低秩分量yw和稀疏分量s的正则化参数.
2 基于可迭代的深度网络方法
2.1 轮换迭代求解策略
对式(10)的问题模型采用轮换迭代求解策略,将其转化为两个优化子问题,分别为低秩分量的最小化问题求解和稀疏分量的最小化问题求解:

对于子问题(11),可采用奇异值阈值 (singular value thresholding,SVT) 法求解低秩分量的近端映射[19]:

对于子问题(12),可采用软阈值法求解稀疏分量的近端映射:


在yw和s的传统迭代求解过程中,迭代收敛的条件取决于选取合适的正则化参数 λ1和λ2,而 λ1和λ2通常需要不断试错调整后手动设定,且奇异值阈值和软阈值操作的阈值也需提前给定,这将导致迭代计算过程繁琐且难以得到最佳取值.因此,为了克服上述不足,本文采用深度学习的框架来展开优化该迭代算法,上述参数在网络训练中将作为可学习参数不断更新以达到最优值.
2.2 可学习迭代展开网络结构
在深度学习的框架下,展开一个迭代算法能够加速算法的收敛,而迭代算法提供了一种自然的递归架构,可解决特定的问题.在深度学习中可将迭代算法的每一次迭代看作深度学习网络中的一层,然后将这些层连接起来,通过训练这种网络架构来提高迭代的收敛性,显著减少迭代次数[21].因此,本文基于深度网络架构将2.1 节中的迭代算法展开,提出相应的递归神经网络模型,第k次迭代对应前馈网络的第k层.在神经网络框架中,使用卷积层来代替矩阵乘法.因此,根据式(14)和(16)来形成一个递归神经网络,将依赖 Φ和 Ω的六个矩阵均替换为适当大小的二维卷积核···,由此可以得出多层前馈网络中第k+1层的方程:

式中,*表示一个卷积算子.在网络训练过程中,这些卷积核是可学习的.利用卷积层空间不变性的优势,可显著减少学习参数的规模,从而加速训练过程.
图3 给出了展开算法的网络架构图.在网络训练过程中,将获取到的雷达回波数据经过测量矩阵 Φ压缩采样后,得到CS 测量向量B作为网络的输入,同时初始化=0、s0=0后进行可学习迭代网络重建,网络中的每一层对应一次迭代求解,经过第K层后得到最终的低秩分量输出和稀疏分量输出sK,而稀疏输出sK即为雷达探测目标重建图像.

图3 展开算法的网络架构Fig.3 Network architecture of the untoued algorithm
图4 为单层网络的架构图,每层网络都包含卷积层和激活层,卷积层中使用六个卷积核(,···,)与卷积层的输入进行交替卷积运算,卷积层输出xy对应式(17)中的对应式(18)中的在卷积层后连接激活层,激活层中进行奇异值和阈值操作,独立学习每层的阈值系数,分别得出对应低秩分量和稀疏分量的迭代解.
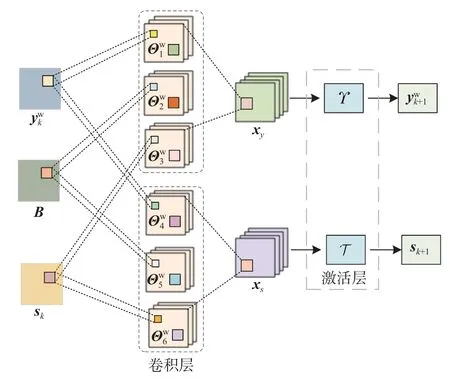
图4 单层网络架构图Fig.4 Architecture of single-layer network
在网络训练过程中,第k层奇异值阈值的实际阈值由给出,软阈值操作的实际阈值由·αs·max(sk)给 出,其中:σ(x)=1/(1+e-x)为 sigmoid 函数;αy和αs为给定的固定标量,αy=0.4,αs=1.8;而每层的和在网络训练中是可学习的.将目标真值标签图像G作为网络的标签数据,G可通过模拟被探测目标的分布得出.整个训练网络采用反向传播的监督方式,损失函数定义为网络预测的图像sK与标签图像G之间的均方误差之和:
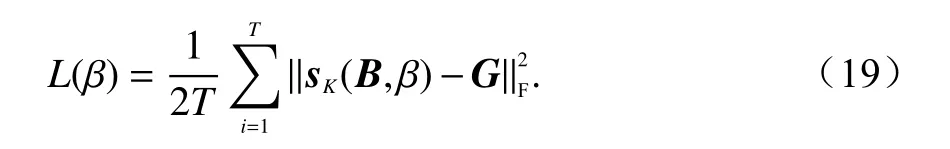
式中:T为数据集的数量;sK(B,β)为具有可学习参数的网络稀疏输出,K为网络层数.
本网络基于PyTorch 神经网络框架实现,Pytorch通过自动微分功能执行反向传播.整个网络使用自适应矩估计(adaptive moment estimation,ADAM)优化器进行训练,学习率设置为0.001,训练数据集为电磁波传播仿真软件gprMax 仿真后得到的200 组不同场景下的雷达回波数据.整个网络共有12 层,前3 层使用的卷积核大小为5×5×1、步长为(1,1,1)、填充为(2,2,0)和一个偏置项,而后9 层使用的卷积核大小为3×3×1、步长为(1,1,1)、填充为(1,1,0)和一个偏置项.表1 为展开迭代深度网络算法流程图.

表1 展开迭代深度网络算法流程图Tab.1 Flowchart of the expand iterative deep network algorithm
3 实验结果分析
为验证本文方法的有效性及准确性,采用基于时域有限差分法的软件gprMax 进行雷达探测场景的仿真.在本文实验中,gprMax 的激励源为中心频率1 GHz 的Ricker 波,收发一体天线阵元在扫描过程中移动间隔为0.02 m,测线位置上阵元数M=43,每个测量位置的频点数N=64.成像区域大小设置为1 m×1 m,并将成像区域划分为51×51 个成像网格.雷达回波数据中加入信噪比(signal to noise ration,SNR)为20 dB 的复加性高斯白噪声,再通过测量矩阵 Φ来进行降采样,从64×43=2 752 个频域样本数据中随机选择1 200 个数据进行成像.图5 探测场景中探测目标P=1,墙体设置为相对介电常数 εw=6的单质混凝土,厚度为0.1 m,墙后目标为半径0.13 m 圆柱形物体,其中心位置位于墙体后方0.54 m 处.图6探测场景中探测目标P=2,墙体设置为相对介电常数 εw=6的单质混凝土,厚度为0.1 m,墙后目标分别是两个半径为0.12 m 和0.1 m 的圆柱形物体,其中心位置分别位于墙体后方的0.54 m 及0.3 m 处,两个目标物体的中心位置相距0.56 m.两图中白色实线标注的为目标所在区域.

图5 单目标仿真及成像结果对比Fig.5 Single target simulation and imaging results comparison
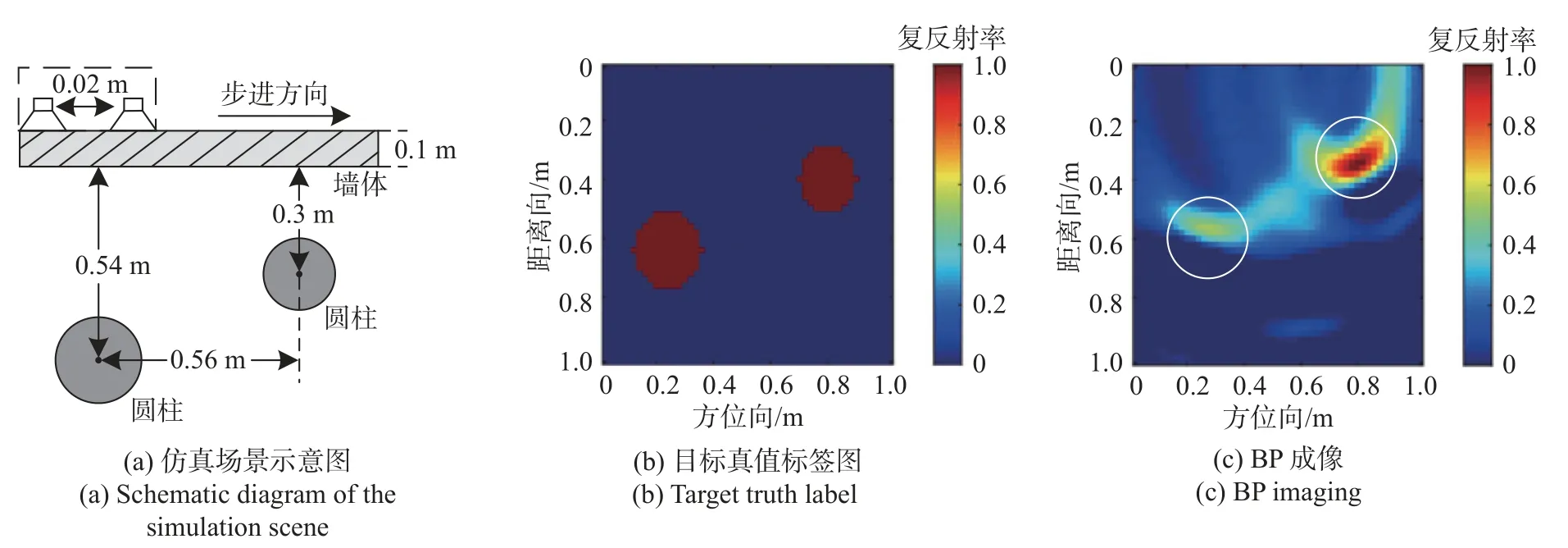
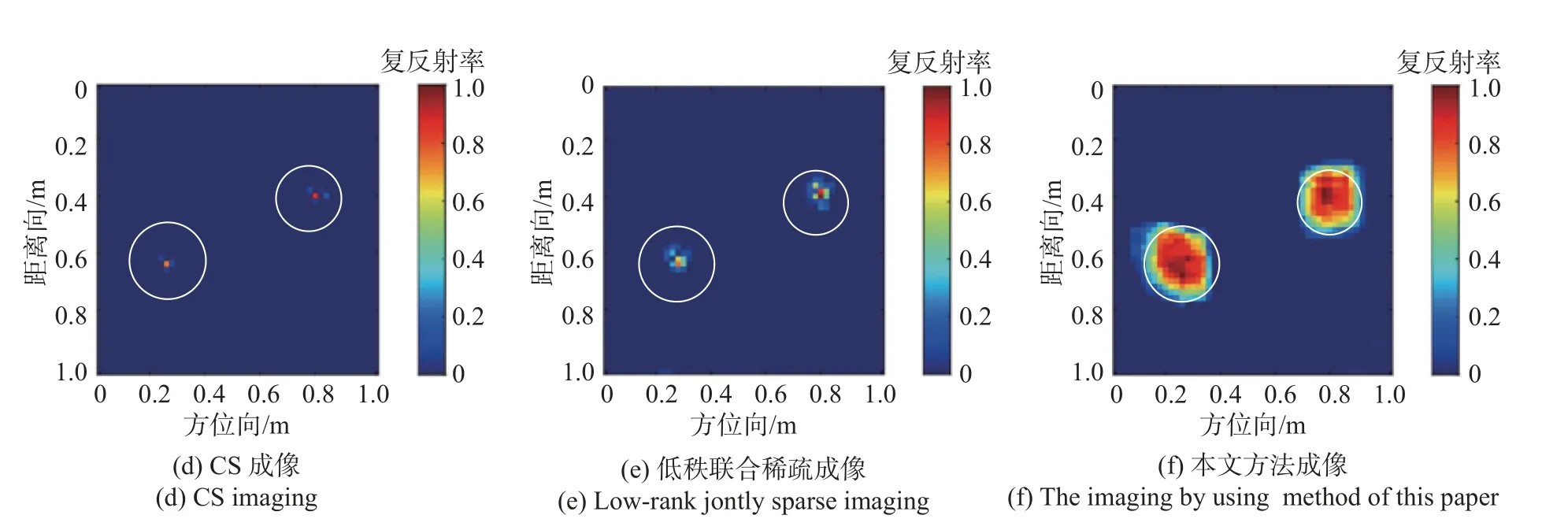
图6 双目标仿真及成像结果对比Fig.6 Double target simulation and imaging results comparison
为研究本文方法的可靠性和准确性,采用经典的后向投影(back projection,BP)算法、CS 算法、低秩联合稀疏迭代重建的方法和本文方法进行成像比较,结果如图5(c)~(f)及图6(c)~(f)所示.从两种场景的成像结果都可以看出:BP 成像的结果存在较多的虚像,成像精度不够高;CS 成像和低秩联合稀疏迭代重建的结果能够较为准确地实现墙后目标的定位,但是成像的轮廓与真值标签图仍存在一定差距;而本文算法不仅能够准确实现目标的中心定位,同时也增强了目标的轮廓特性,更加接近目标重建真值图,明显优于前述成像结果.
为定量比较以上4 种算法的成像重建性能,采用目标杂波比(target-to-clutter ratio,TCR)、峰值SNR(peak SNR,PSNR)和程序运行时间(program running time,PRT)作为定量评价标准.TCR 用来评估图像的聚焦度,TCR 值越高,图像的聚焦度越高;PSNR 用来评估图像的失真度,PSNR 值越高,图像的失真越少;PRT 用来评估算法运行时间,PRT 值越小,PRT 越短.
TCR(单位dB)定义为

式中:Nt和Nc分别表示成像结果中的目标区域和杂波区域所对应的像素个数;At和Ac分别表示成像结果中的目标区域和杂波区域;Iq表示第q个像素点的像素值.
PSNR(单位dB)定义为

式中:G(i,j)表 示真值标签图像;H(i,j)表示重建目标图像.
表2 及表3 分别给出了单目标场景和双目标场景下4 种成像算法成像重建性能对比结果.反复进行100 次实验后求平均值,得出4 种算法的TCR值、PSNR 值和PRT 值.可以看出,低秩联合稀疏成像的TCR 值较高,但其PSNR 值较低,PRT 值最高,说明该方法图像存在失真且耗时长.本文方法的TCR 值、PSNR 值和PRT 值都为最佳,说明本文所提方法的成像质量最高,且更能满足实时性要求.

表2 单目标重建性能对比Tab.2 Comparison of single target reconstruction performance

表3 双目标重建性能对比Tab.3 Comparison of double target reconstruction performance
图7 分别给出了雷达回波数据中加入SNR 为0~60 dB 的复加性高斯白噪声下重建目标图像的TCR 值及PSNR 值.可以看出,不论是单目标场景还是双目标场景,本文所提出的方法在低SNR 的情况下,重构图像依然具有较高的TCR 值和PSNR 值,表明能够有效地抑制墙体杂波,重构出高精度的目标图像,且在SNR 大于20 dB 时,本文方法的图像重建性能接近稳定.

图7 不同噪声水平下的TCR 和PSNRFig.7 TCR and PSNR at different noise levels
4 结 论
本文提出了一种基于深度迭代网络的TWRI 方法,该方法将成像问题转化为联合低秩与稀疏分解驱动的优化问题,并将求解算法展开到深度网络结构中,替代原有的迭代求解方法形成了物理模型驱动的深度网络求解框架.实验结果分析表明,该方法能够实现比其他方法更好的性能,兼顾了图像重建精度和计算复杂度.在后续工作中,将继续探究该框架下的雷达成像算法,致力于将该方法更加完善地应用于更真实、更复杂的成像场景中.

