Al 含量对γ-TiAl 合金断裂行为的影响

梁月慧，祁文军

（新疆大学机械工程学院,新疆 乌鲁木齐 830017）

0 引言

γ-TiAl 合金是一种具有面心四方结构的新型金属间化合物，因其具有低密度、高温强度、高比强度、良好的抗蠕变性以及抗氧化性和耐腐蚀性等优点而成为航空航天领域的研究热点[1-2]。目前，该合金材料在航空航天中的应用主要有发动机、起落架、框、梁、机身蒙皮、隔热罩等零部件[3-11]。在实际应用过程中，γ-TiAl 合金中不可避免地会存在各种各样缺陷和损伤，缺陷和损伤的进一步演变会严重影响材料的使用性能，甚至导致材料失效。因此，深入研究这些缺陷和损伤对γ-TiAl 合金力学性能的影响有助于我们更好地了解γ-TiAl 合金，使其更有实际应用价值。材料的失效虽然是宏观现象，但实质上是在原子尺度上决定的，而分子动力学作为一种原子、分子尺度上进行微观特性研究的有力工具，成功地应用于晶粒的生长、拉（压）应力-应变关系、高低温变形行为、晶格畸变、孔洞与堆垛层位错等缺陷的演化、形变过程等众多领域的研究，取得了很多成果。

方洲等人[12]运用分子动力学方法研究了含裂纹、孔洞铝的裂纹扩展行为，研究表明孔洞直径越大，在孔洞内边缘越易产生大量滑移和位错。Feng等[13]采用分子动力学方法分析了不同温度和不同空位浓度对γ-TiAl 合金力学性能的影响，研究表明试样的极限应力、极限应变和弹性模量随温度和空位浓度的升高呈非线性下降。Takeuchi 等人[14]运用分子动力学方法对单晶γTiAl 合金和α2-Ti3Al 合金中的位错行为进行了研究分析，研究发现：理想位错会分解成不完全位错和堆垛层错；温度1 000 K时位错运动少于温度为300 K 时位错的运动。张玲等人[15]运用分子动力学研究循环交变载荷方式对单晶γ-TiAl 合金性能及裂纹扩展的影响，研究结果表明单晶γ-TiAl 合金在交变载荷的循环加载下不同阶段的裂纹扩展机理及塑性变形机制完全不同。以上成果表明，研究孔洞、温度、空位浓度和加载速率对材料力学性能的影响在分子层面的机理越来越重要。因此，研究Al 成分含量对γ-TiAl 合金力学性能的影响是有必要的。

γ-TiAl 合金的力学性能与组织形态密切相关，而组织形态又受本身成分影响，关于Al 含量对γ-TiAl 合金力学性能的影响主要采用试验方法开展研究，而从原子层面分析不同Al 含量对γ-TiAl 合金力学性能影响的相关探讨较少。针对微观尺度上不同Al 含量对γ-TiAl 合金微观形变机制影响的研究不足，笔者通过分子动力学研究分析了铝含量对单晶γ-TiAl 合金总能量和应力-应变的影响，探究了Al 含量在45%～49%范围内的单晶γ-TiAl 合金的微观缺陷演化过程，为γ-TiAl 合金的理论研究和实际应用提供了一定的参考价值。

1 γ-TiAl 合金模型的建立和计算方法

γ-TiAl 合金的晶体结构是L10型面心四方（FCT）晶体结构[16]，如图1 所示。X、Y、Z分别对应TiAl的[010]、[100]和[001]晶向。

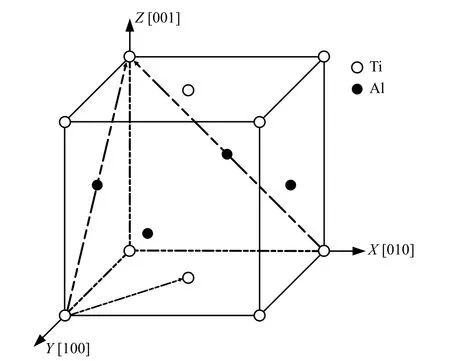
图1 γ-TiAl 的L10 晶体结构Fig.1 L10 structure of γ-TiAl

分子动力学模型首要环节是根据模拟情况来确定合适的原子间相互作用势，Zope R R[17]等人采用嵌入原子势（EAM 势）研究了γ-TiAl 的物理性能，模拟数值与试验数值基本吻合，所以笔者采用嵌入原子势（EAM 势）来描述γ-TiAl 原子间的相互作用。此次分子动力学研究使用LAMMPS[18]开源软件进行模拟计算。运用ATOMSK[19]软件建立初始模型，如图2 所示，Ti、Al 原子沿[001]方向交替堆列（绿色为Ti 原子，红色为Al 原子）。所建立的模型大小为40a×20b×20c，为了避免原子在模型盒子边界处可能会产生的重叠，设置模型盒子大小沿X、Y和Z方向上的盒子长度为晶格常数的整数倍。其中，晶格常数a=b=0.400 1 nm，c=0.418 1 nm。模型共有32 000 个原子，随后使用ATOMSK 软件将不同百分比的Al 原子随机替换为Ti 原子，从而获得具有不同Al 含量的γ-TiAl 模型，图3 为使用ATOMSK软件随机将5%Ti 原子替换为Al 原子得到的Ti45Al 合金原子模型。笔者研究了在300 K 温度下Al 含量分别为45%、46%、47%、48%、49%时对γ-TiAl 合金力学性能的变化，进而选择45%Al 含量的模型进行缺陷分析。45%Al 含量下的微观缺陷演变过程不仅能体现其他Al 含量下γ-TiAl 合金的微观缺陷演变的共性，同时还具有其他Al 含量下γ-TiAl 合金缺陷演变所没有的特性，即在此演变过程中产生了Lomer-Cottrell 位错，Lomer-Cottrell 位错的形成阻碍了位错、层错发射，减缓了层错的运动速度，使γ-TiAl 合金的塑性变强，因此还单独分析了Al 含量为45%时不同时刻的原子运动轨迹[20]，过程如图4 所示。为了后期的分析过程直观明了，本次研究的载荷加载方向为X方向。由于计算机自身的限制，不能模拟计算含粒子数太多的体系，然而这样会导致尺寸效应，影响模拟结果的准确性。为了减少尺寸效应与计算量，分子动力学研究时通常采用周期性边界条件，所以XYZ轴均采用周期性边界条件。

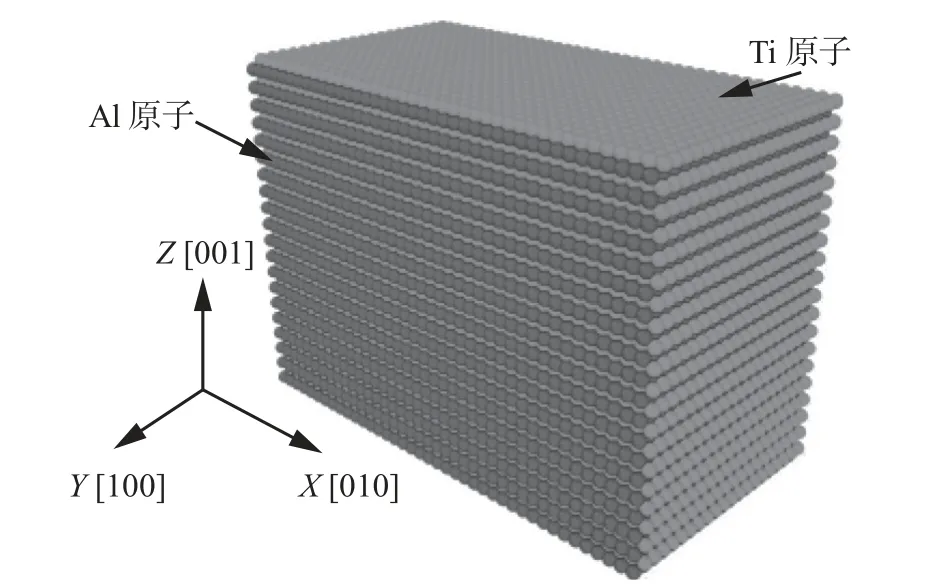
图2 γ-TiAl 合金的原子模型Fig.2 Atom model of γ-TiAl alloy

图3 γ-Ti45 Al 合金的原子模型Fig.3 Atom model of γ-Ti45Al alloy

笔者采用恒定的应变速率加载方式进行拉伸研究，研究计算过程分为弛豫和加载两个阶段。因加载前模型体系是不平衡的，为使其处于平衡状态，将不同Al 含量的γ-TiAl 合金在等温等压系综（NPT）下进行弛豫10 ps，使体系中的总能量达到稳定状态，弛豫过后再对模型进行拉伸加载，加载过程采用正则系综（NVT），整个模型拉伸过程中温度都是300 K，因此运用Nose-Hoover 热浴方法进行控温，Velocity-Verlet 算法计算原子运动轨迹，时间步长设置为0.001 ps，应变速率为1×109s-1，沿X方向进行单轴拉伸。整个研究过程共运行300 万步，每隔1 000 步记录γ-TiAl 合金模型拉伸过程的动能、势能、总能量、应力应变值。对单晶γ-TiAl 合金的拉伸过程和结果采用 Open Visualization Tool(OVITO)[21]进行结果可视化分析和处理。

2 结果与分析

2.1 Al 含量为45%时的γ-TiAl 合金的微观缺陷演变

图4 显示了Ti45Al 不同时间的断口，（a）～（g）为不同时刻的原子轨迹，（a1）～（g1）为采用OVITO中的Dislocation analysis(DXA)分析结果，在整个拉伸加载过程中，单晶γ-TiAl 合金内部存在着大量的原子结构变化以及晶体结构的转变，图3 中的绿色原子为单晶γ-TiAl 合金原始的FCT 结构，红色原子为层错和堆垛层，白色原子为不满足任何基本原子结构的无序原子，这种无序结构原子数目偏少，一般不是整体的无序变化，只是微观的表现形式。图4（a）为0 ps 时原子轨迹，随着加载时间的增加，出现大量无规则排列的无序原子。图4（b）所示，当t=201.8 ps时，第一个位错开始形核并以位错环的形式开始向[112]方向发射滑移，这为形成层错提供有利条件，标志着塑性变形的开始。图4（c）（d）表示在t=206.5 ps时，原子团簇堆积形成堆垛层错，导致晶格发生畸变。如图4（e）所示，在堆垛层错附近，原子与其邻近原子的配合位置存在的错位会产生应力集中，随着加载的继续，新形成的位错源进一步形成位错形核并发生相向滑移。如图4（f）所示，在t=218.9ps处时可以观察到罗曼-柯垂尔（Lomer-Cottrell）位错，随着加载的继续，堆垛层错m1 与m2 在相对滑移后相遇交截线就形成了Lomer-Cottrell位错锁，Lomer-Cottrell位错锁如图5所示，Lomer-Cottrell 位错锁在两个平面上成为了位错进一步滑移的障碍，阻碍了其它位错的滑移，产生位错强化效应，在一定程度上提高了材料的强度，体系应力也因此达到峰值12.24 GPa。如图4（g）所示，原子团簇因阻碍作用在m1、m2 下方不断塞积，由此萌生的空位和多原子空位孔洞式缺陷使得此处的应力不断增大，从而导致模型材料塑性增强。如图4（h）所示，原子的不断迁移导致空位增多，体系应力快速下降，不同位置的空位又形成多个孔洞并逐渐发展扩大，它们最终汇聚成一条裂纹，因而造成材料的断裂。研究结果表明：在变形初期，随着弹性变形的加剧，层错数量增加；变形后期，层错数量迅速减少。随着加载时间的增加，材料内部出现了空位、孔洞，在t=220.5 ps 时堆垛层错结束滑移，贯穿成一条裂纹，形成断口，最终导致γ-TiAl 模型断裂。对其他Al 含量的γ-TiAl 合金的微观缺陷演变也做了分析和研究，如表1 所示。

表1 不同Al 含量的γ-TiAl 合金微观缺陷演变时间Table 1 Evolution time of microdefects in γ-TiAl alloys with different Al contents

图4 不同时刻Ti45Al 的原子运动轨迹Fig.4 Atomic trajectories of Ti45Al at different moments

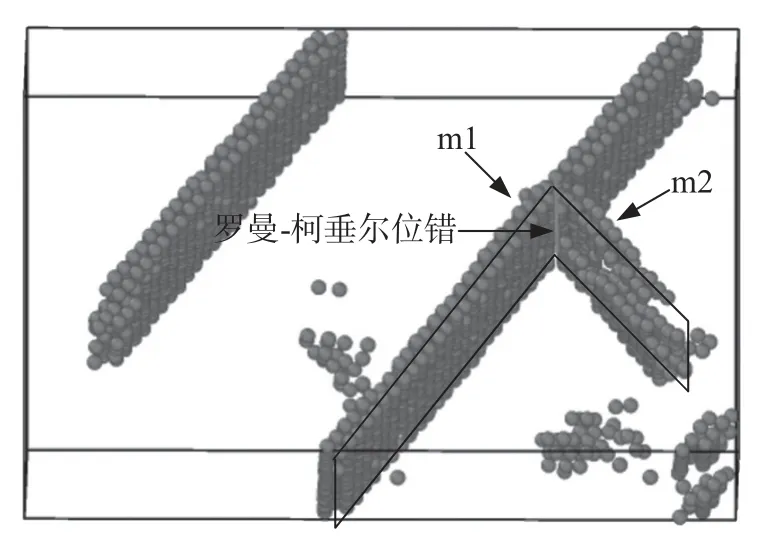
图5 罗曼-柯垂尔位错锁Fig.5 Lomer Cottrell dislocation lock

随着Al 含量的增加，屈服强度随之下降，TiAl合金的位错发射时间提前，导致变形提早发生，使模型会更早的产生孔洞、位错以及缺陷。因此在Al含量高的模型中，由于缺乏缺陷间的相互作用，模型更容易发生断裂，TiAl 合金的塑性也随之变差。所以在同等条件下，当TiAl 合金中的Al 含量在45%～49%的范围内，Al 含量较低的TiAl 合金其塑性越好。

2.2 γ-TiAl 合金在弛豫和加载下的总能量变化

为了研究分析Al 含量对单晶γ-TiAl 合金裂纹扩展的影响，从研究结果中拟合了弛豫和加载过程中的总能量变化曲线。图6 是弛豫过程中不同Al含量下单晶γ-TiAl 合金的总能量随加载时间的演变过程。从图6 可以看出，在弛豫过程中Al 含量分别为45%、46%、47%、48%、49%时，γ-TiAl 合金的总能量达到平衡状态的均值分别是-138 705、-139 321、-139 929、-140 537、-141 138 eV。随着Al 含量的降低，γ-TiAl 合金的弛豫总能量的峰值略有增大，总能量达到平衡状态的均值在增加。这是由于Al 含量的降低，在相同的加载时间步数内，体系原子的位错滑移增大，原子相对运动的剧烈程度增大。故可知不同Al 含量对单晶γ-TiAl 合金弛豫过程中总能量的变化有一定的影响。图7 是拉伸过程中不同Al 含量下单晶γ-TiAl 合金总能量随时间的演变曲线。初始加载时，内部原子开始运动原子，结构发生变化，动能增加，势能也从平衡状态开始上升，γ-TiAl 合金内部原子总能量开始上升至峰值，此阶段是γ-TiAl 合金的弹性变形阶段。随着加载时间的不断叠加，模型中的大量原子形成位错，堆垛层、孔洞、体系总能量迅速下降，结合图4 原子运动轨迹图可知，此时模型已经产生位错、孔洞和裂纹现象，这就解释了拉伸过程总能量曲线只有一个波峰没有出现上下波动的现象。

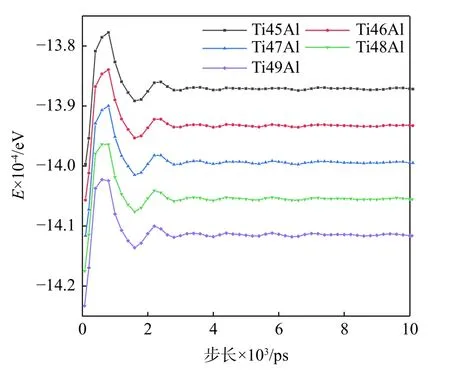
图6 弛豫过程中总能量随时间的演变过程Fig.6 Total energy as function of loading time during relaxation process

图7 拉伸过程中总能量随时间的演变Fig.7 Total energy as function of loading time during tensile process

2.3 不同Al 含量下的应力-应变曲线分析

为了更好地理解不同Al 含量的γ-TiAl 合金的力学性能，图8 给出了常温下（300 K），Al 含量在45%～49%范围内的应力-应变曲线，从图8 可以明显地观察到整个体系在拉伸载荷作用下经历了两个阶段：弹性变形阶段、塑性变形阶段。在模型的拉伸过程中，由于晶格畸变单一晶体中Ti 对单晶有增强作用，应力应变曲线中弹性阶段呈非线性趋势；不同Al 含量的γ-TiAl 合金应力应变曲线在弹性阶段变化趋势基本一致，应力在弹性变形阶段逐渐上升，都是随应力的增大，应变也随之逐渐增大，应力值达到最大值，称为屈服应力；当应力达到最大值后，应力迅速下降到最小值，最后在零附近波动，表明材料是脆性断裂。从图8 可以看出，Al 含量从45%～49%时，弹性模量分别为56.4、56.2、55.9、55.6、55.5 GPa。屈服应力分别为12.24、12.06、11.75、11.57、11.22 GPa。随着Al 含量的增加，材料的弹性模量和屈服应力均有所降低。从应力-应变曲线的局部放大可以得出屈服应力规则变化的结果，表明屈服应力随Al 含量的增加而降低。随着Al 含量的增加，应力-应变曲线的斜率略微下降，使材料变形较容易。在此次研究过程中，当Al 含量在45%～49%时，TiAl 合金的屈服应力与Umeda H[22]和Zhang W J[23]的试验结果显示出相同的关系，TiAl 合金的屈服应力随着Al 含量的降低而增大。图8 中材料断裂后曲线出现波动，原因是位错反应以及空位、堆垛层错的产生，所有这些都会释放或积累应力，使得应力应变出现波动现象。应力之所以呈现这样的变化不仅与TiAl 合金的相组成有关，还和原子键之间的连接方式有关（Ti-Ti 键、Ti-Al 键、Al-Al 键）。各键上的电子数决定了位错形成的难易程度[24-25]。

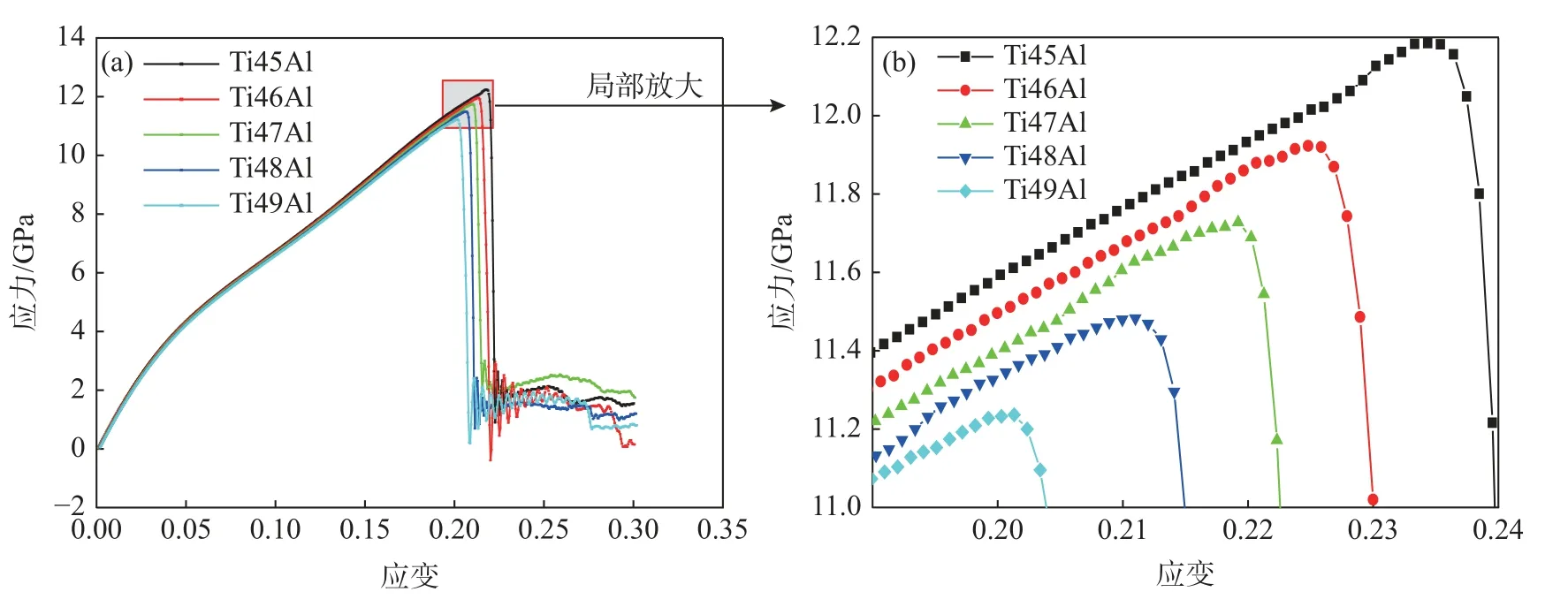
图8 不同Al 含量的γ-TiAl 合金的应力-应变曲线Fig.8 Stress-strain curves of γ-TiAl alloys with different Al contents

3 结论

对于γ-TiAl 合金，Al 含量在45%～49%范围内，可以得出以下结论：

1）Al 含量会影响材料裂纹的扩展行为，在演变过程中Al 含量为45%时产生了Lomer-Cottrell 位错。而在其他Al 含量下没有观察到Lomer-Cottrell 位错，只观察到Ti45Al 中出现的空位、堆垛层错。位错数量及类型减少，使材料断裂时间提前。

2）Al 含量对γ-TiAl 合金的弹性模量和屈服应力的影响较小，随着变形的加剧，层错数量均是先增加后减少。

3）随着Al 含量的减少，弛豫过程的总能量均值增加，拉伸过程的总能量峰值增加。