分数阶混沌系统的无源反步控制器设计
赵飞,郑永爱
(扬州大学信息工程学院,江苏 扬州 225127)
最近,学者们提出了多种混沌系统的控制和同步方法[1-10]。其中,反步控制是一种将李雅普诺夫函数的选择与反馈控制器的设计相结合的系统控制方法。文献[11-13]利用反步控制法实现了整数阶和分数阶混沌系统的控制和同步。无源控制是从系统的能量角度入手,使闭环系统满足无源性的一种控制方法,从而实现系统的稳定性。利用无源控制,文献[14]和文献[15-16]分别实现了超混沌系统和分数阶系统的控制和同步。结合反步控制和无源控制技巧,该文提出了实现分数阶混沌系统的无源反步控制法。
1 预备知识
Caputo 微分定义为[17]:

其中,n-1 <α<n,n∈N,Γ(·)为伽马函数。非自治分数阶系统如式(2):

其中,α∈(0,1)是分数阶,x=(x1,x2,…,xn)T是系统的状态变量,f=(f1,f2,…,fn)T是可微的非线性向量函数。
引理1[18]设x=0 是式(2)系统的平衡点,若存在李雅普诺夫函数V(x(t),t) 和K 类函数γi(i=1,2,3)满足式(3):
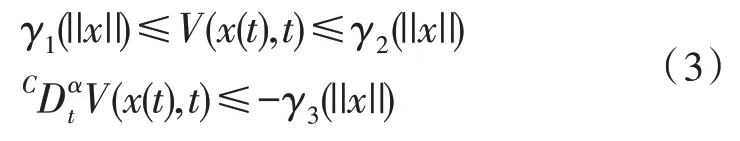
那么式(2)系统是渐近稳定的。
引理2[19]若x(t)为连续可微函数向量,则有:
分数阶系统如式(5):
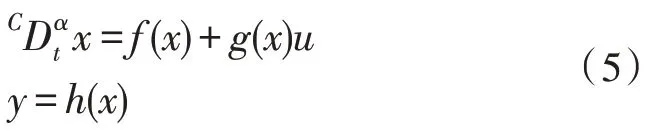
其中,x∈Rn是状态变量,u∈Rm是输入变量,y∈Rm是输出变量,f(x)和g(x)是光滑向量场,h(x)是光滑映射,且f(0)=h(0)=0。
假设式(5)系统可以用式(6)表示:
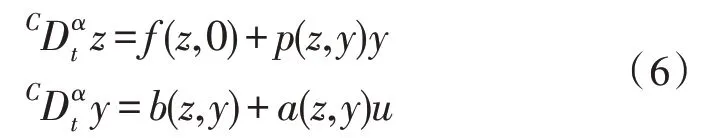
其中,(zT,yT)T∈Rn是系统的新坐标,z∈Rn-m是状态变量。
定义1如果存在一个正定李雅普诺夫函数V(z,y)(称为存储函数或能量函数),满足对任意的t≥0有≤uT y,则式(6)系统是无源的。如果存在一个正定李雅普诺夫函数V(z,y)和一个K 类函数γ4,满足对任意的t≥0 有:
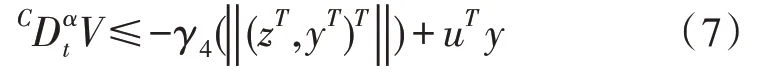
则式(6)系统是严格无源的。
由引理1 易得下面的引理3:
引理3假设式(6)系统是严格无源的,则式(6)系统的平衡点x=0 在输入u=0 的情况下是渐近稳定的。
2 分数阶混沌系统的无源反步控制设计
将利用反步控制研究分数阶混沌系统的无源控制问题,系统描述如下:
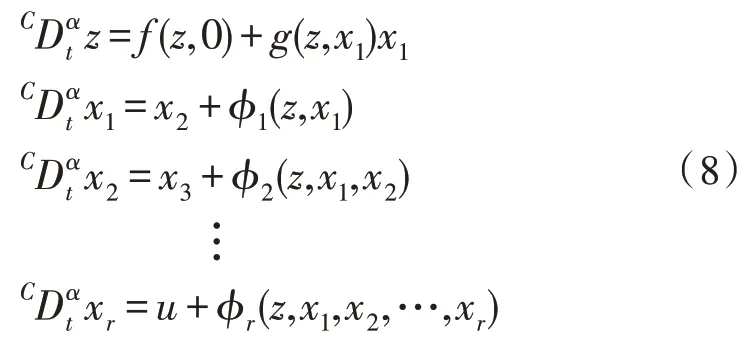
其中,α是分数阶阶次,z∈Rn-r,(x1,x2,…,xr)T∈Rr是状态,u∈R是输入,函数f(·)、g(·)和φi(·)(i=1,2…,r)都是光滑函数,且f(0,0)=0,g(0,0)=0,φi(0,0)=0(i=1,2,…,r)。
定理1若函数f(z,0)满足zT f(z,0)≤-|z|2l(z),其中l(z)是光滑函数,且对于任意的z,都有l(z)>0,则存在如下反馈控制器(式(9)),使得式(8)系统是严格无源的,且在外部输入信号v=0 的情况下是渐近稳定的。
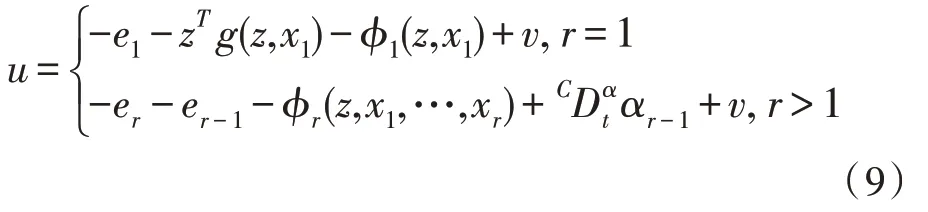
其中,α1=-e1-zT g(z,x1)-φ1(z,x1)与αi=-ei-ei-1-φi(z,x1,…,xm)+(i=2,…,r-1) 为设计的虚拟控制器,且转换变量e1=x1、ei=xi-αi-1(i=2,…,r)。
证明设计步骤共有r步,第1 步:设x2为控制器,α1为虚拟控制器。由于e1=x1、e2=x2-α1,则有子系统:

第i(2 ≤i<r)步:设xi+1为实际控制器,αi是虚拟控制器。由于ei+1=xi+1-αi,则有子系统:

从而由定义1 知,式(12)子系统是严格无源的。
第r步:式(8)系统变为:
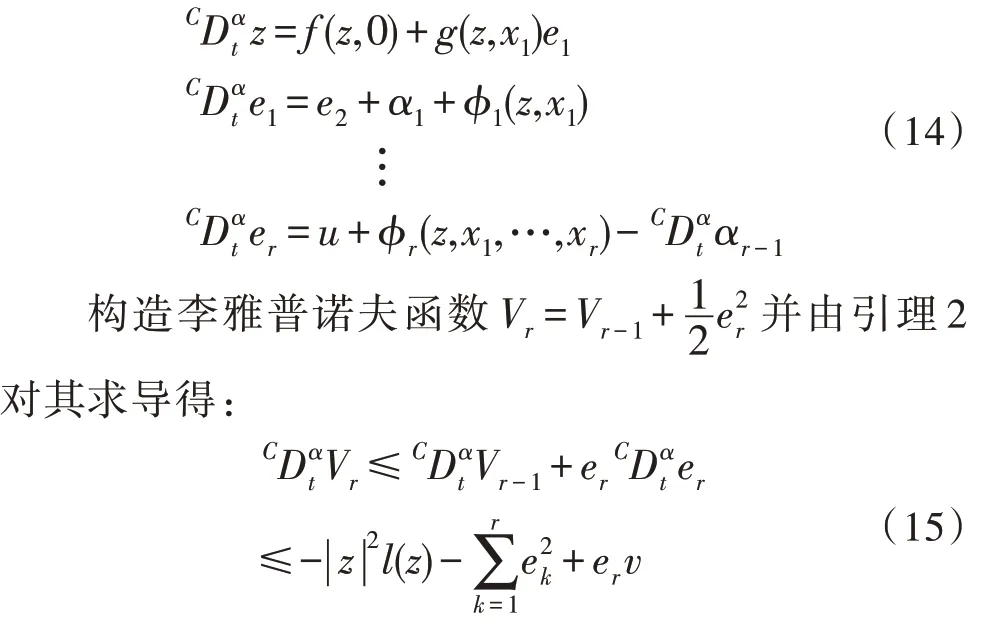
所以由定义1 知,式(14)系统是严格无源的。即式(8)系统是严格无源的。进一步由引理3 知,在输入v=0 的情况下,式(8)系统也是渐近稳定的。
3 数值仿真
例1 考虑如下分数阶Shimizu-Morioka 混沌系统[20]:
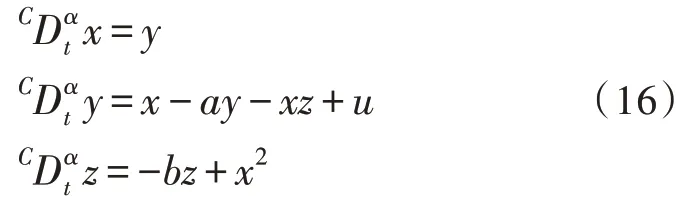
其中,x、y、z是状态变量,u∈R是输入,0<α≤1是分数阶阶次,a∈R、b∈R+是参数。当α=0.98、a=0.75、b=0.45,初始条件为x=0、y=0.25、z=1 时,系统呈现混沌现象。分数阶Shimizu-Morioka系统的混沌吸引子如图1 所示。
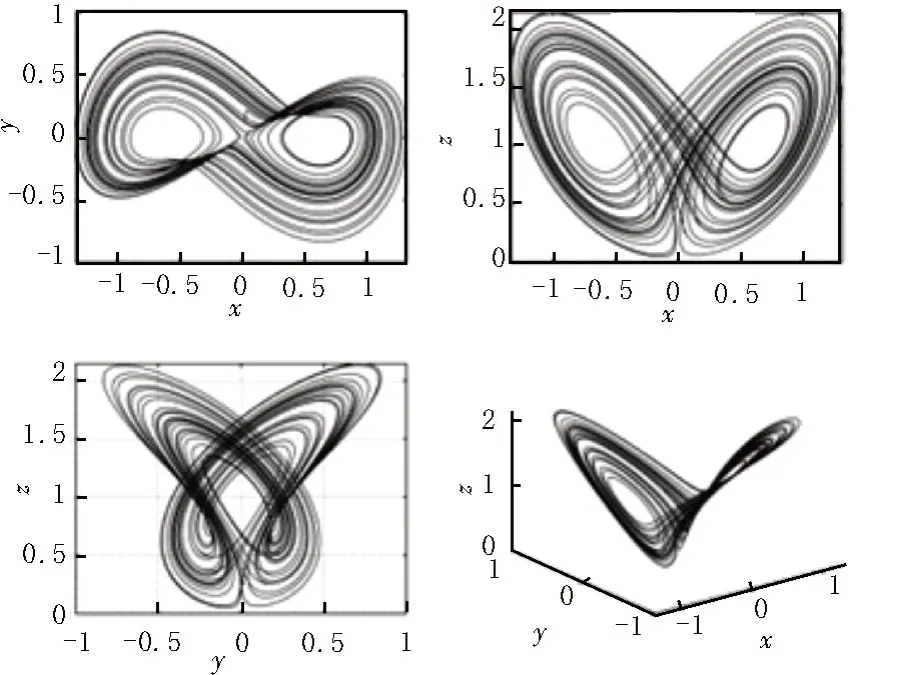
图1 分数阶Shimizu-Morioka系统的混沌吸引子
设z=z、x1=x、x2=y,式(16)系统可表示为如式(8)的形式,如式(17):
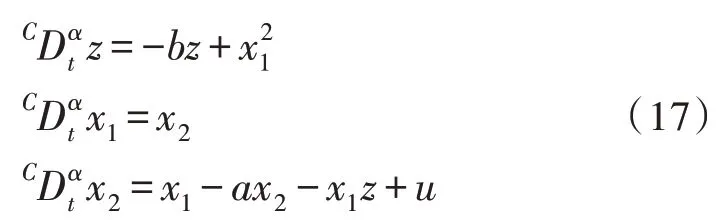
对于式(17)系统,n=3,r=2,f(z,0)=-bz,zf(z,0)=-bz2,l(z)=b>0 满足定理1 的条件。根据定理1,在虚拟控制律α1=-e1-ze1与控制律u=-2e1+ae2+aα1+e1z+CDα t α1-e2+v作用下,式(17)系统是严格无源的,且在输入v=0 的情况下是渐近稳定的。
对于式(17)系统,当α=0.98、a=0.75、b=0.45,初始条件为z=-2、x1=-0.2、x2=-6 时,受控分数阶Shimizu-Moriok 系统的状态响应如图2 所示,结果表明,所设计的控制器能将分数阶Shimizu-Moriok 系统稳定到原点。

图2 受控Shimizu-Moriok系统的状态响应
例2分数阶Lü混沌系统[21]如式(18):

其中,x、y、z是状态变量,u∈R是输入,0 <α≤1是分数阶阶次,a、b、c是正常参数。当α=0.96、a=36、b=3、c=20,初始条件为x=1、y=2、z=2 时,系统呈现混沌现象。分数阶Lü系统的混沌吸引子如图3 所示。
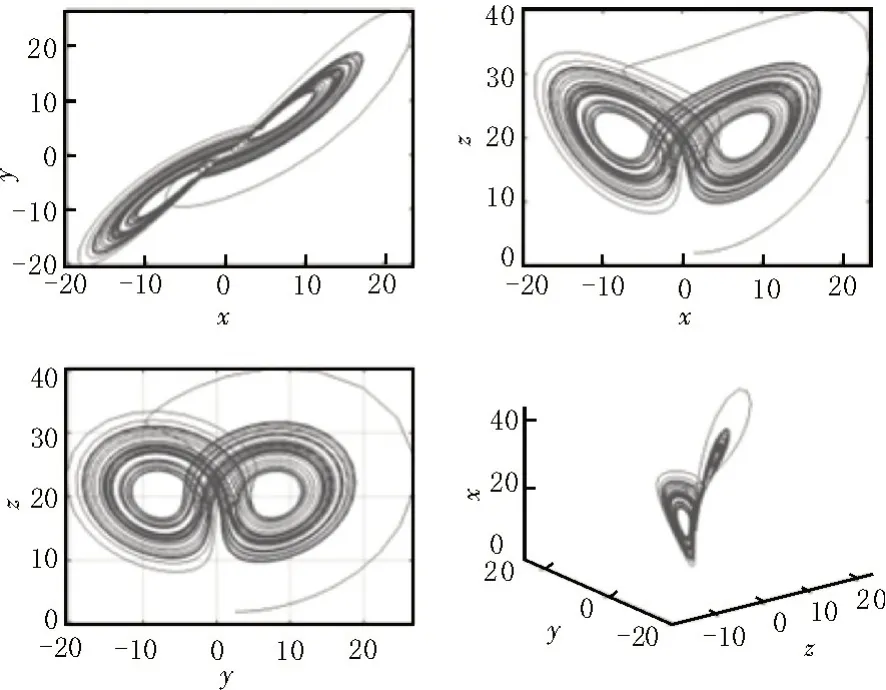
图3 分数阶Lü系统的混沌吸引子
设z1=x,z2=z,x1=y,式(18)系统可表示为如式(8)的形式,如式(19):

对于式(19)系统,n=3,r=1,f(z,0)=(-az1,-bz2)T,(z1,z2)f(z,0)=≤-max{a,b}||z||2,l(z)=max{a,b}>0 满足定理1 的条件。根据定理1,在控制律u=-ce1-az1-e1+v作用下,式(19)系统是严格无源的。且在输入v=0 的情况下是渐近稳定的。
对于式(19)系统,当α=0.96、a=36、b=3、c=20,初始条件为z1=-22、z2=1、x1=16 时,受控分数阶Lü系统的状态响应如图4 所示,结果表明,所设计的控制器能将分数阶Lü系统稳定到原点。
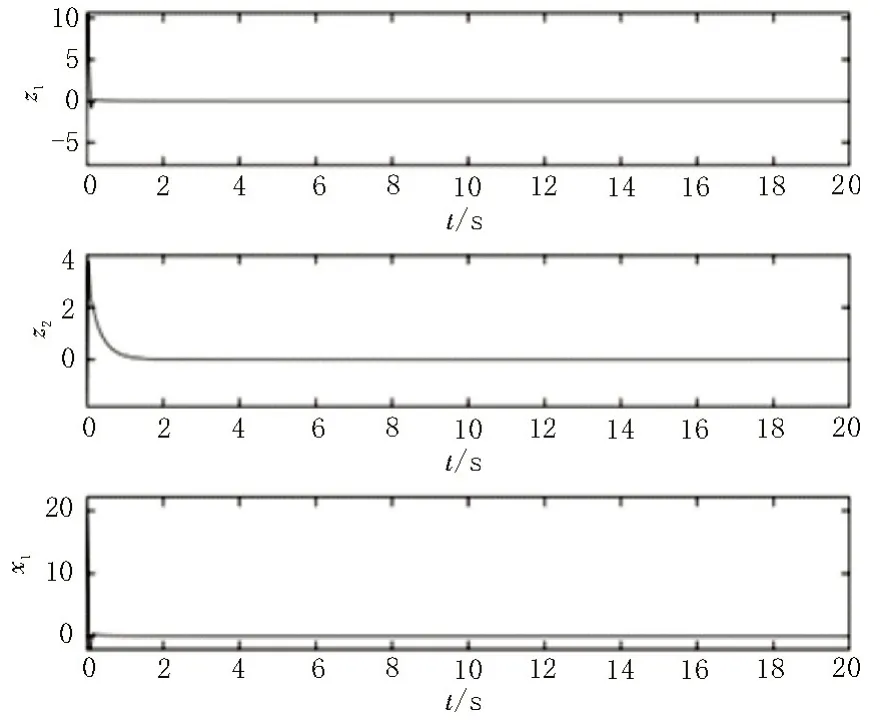
图4 受控分数阶Lü系统的状态响应
针对下面的整数阶Lü混沌系统(式(20)),通过将该文所提方法与文献[11]的反步控制方法做对比,进一步来说明该文所提方法的优越性和研究动机。

该文和文献[11]设计的控制器分别为u=-cx1-az1-x1和u=-(1+c)x1-az1+z1z2,很明显该文设计的控制器是线性控制器,但也具有和文献[11]一样的控制效果,所以该文方法更简单有效。当a=36、b=3、c=20,初始条件为x1=10、x2=10、z=-10 时,受控整数阶Lü系统分别在该文和文献[11]所设计的控制器下的状态响应如图5 和图6 所示。
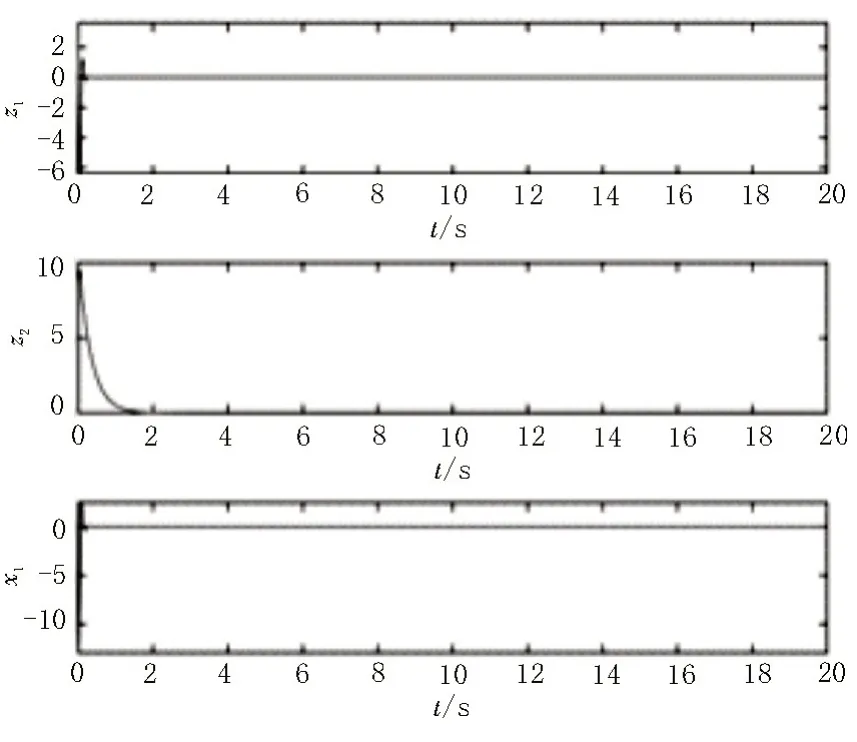
图5 在该文控制器下的状态响应

图6 在文献[11]控制器下的状态响应
4 结论
该文研究了分数阶混沌系统的无源反步控制问题,利用反步控制的递推过程,独立设计每个子系统的能量函数和虚拟控制律,最终设计出整个系统的实际控制律,实现对分数阶混沌系统的无源反步控制。以分数阶Shimizu-Morioka 系统和分数阶Lü系统为例进行数值仿真,理论分析和数值仿真结果验证了该方法的有效性。

