基于卷积神经网络的手写数字识别方法研究

唐鉴波，李维军，赵波，习立坡

（1.陆军工程大学通信士官学校，重庆 400035；2.78118 部队，四川 成都 610000；3.32178 部队，北京 100012）

近年来，机器学习相关理论得到了长足发展，其研究成果可广泛应用于计算机视觉等多个方面，手写数字识别作为计算机视觉的重要分支，可广泛应用于数据统计、财务金融以及成绩判定等领域。人们日常的书写习惯以及不同的书写速度都会导致书写形式出现多种变化，这成为手写数字识别需要克服的一大难点。

当前，国内外出现了较多手写数字识别的研究成果，主流的方法主要是根据图像中数字的结构特征进行特征提取和聚类分析，其代表算法有卷积神经网络、KNN 最邻近算法、决策树算法、向量机算法以及多种人工神经网络算法[1-5]，其中卷积神经网络(Convolutional Neural Network,CNN)作为一种典型的神经网络，被广泛应用于图像识别和分类等领域，它能够较好地识别人脸、物体和交通标志[6]，是机器学习的重要工具。

文中分析了卷积神经网络相关原理，通过Tensorflow搭建CNN 结构，采用Minist 数据集[7]对CNN 的典型模型LeNet-5 进行训练，在对图像进行预处理和数字分割的基础上，实现了准确率较高的手写数字识别，并对实验结果进行了简要分析，文中方法对于手写数字识别的模型搭建和实现具有参考意义。

1 卷积神经网络

卷积神经网络是一类典型的深度神经网络，该网络最早于1984 年由日本学者K.Fukushima 发现并验证，它具有局部感知、权值共享等特性[8]，该网络在计算机视觉研究领域发挥了重要作用[9]。

1998 年，Y.Lecun 等人将卷积层与降采样层相结合，建立了卷积神经网络的现代原型LeNet，该模型后来被广泛应用于手写字符的识别。随后各种基于该模型的手写数字识别改进算法相继出现，文献[10]将卷积神经网络与自动编码器结合，形成了深度卷积自编码神经网络，得到了较好的识别效果；文献[11]对比了三类数据集训练神经网络的实验结果，阐明了训练数据集对识别结果的重要影响；文献[12]在卷积神经网络模型的基础上，基于PCA 特征提取方法，实现了多层卷积核参数初始化的手写数字识别，在提升训练收敛速度的同时获得了较高的识别率。

1.1 卷积神经网络结构

卷积神经网络是一种前馈神经网络[13]，它由一个输入层、一个输出层以及多个处在输入层、输出层之间的隐藏层组成。网络的隐藏层主要包括卷积层、池化层和全连接层[14]，其中卷积层和池化层相结合，主要起到提取图像特征的作用。在获得图像典型特征图的同时，减少输入层到全连接层中的数据量，全连接层则根据输入的特征图，利用多层感知元模型对特征图进行分类识别。图1 所示为卷积神经网络的典型结构，图中省略号表示卷积层和池化层可根据建模需要多次交替出现。

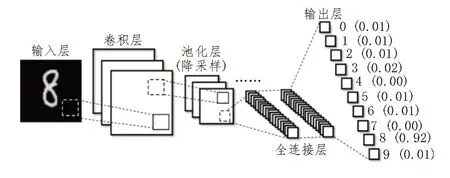
图1 卷积神经网络典型结构

1.2 卷积神经网络关键层功能

卷积神经网络的训练通常涉及到模型中各个层级，每一层在网络中发挥不同的作用，下面对各层的功能和原理进行进一步阐释。

1）卷积层：作为CNN 的核心，卷积层主要用于从输入图像中提取相关特征。它主要由卷积核实现卷积功能，这些卷积核本质上是小尺寸的二维矩阵，它以一定的步长沿原图像自左向右、从上至下“滑动”，每滑动一次即做一次卷积运算，通过上述过程最终得到图像对应的特征图。图2 所示为图像某像素块与卷积核进行卷积的示意图。

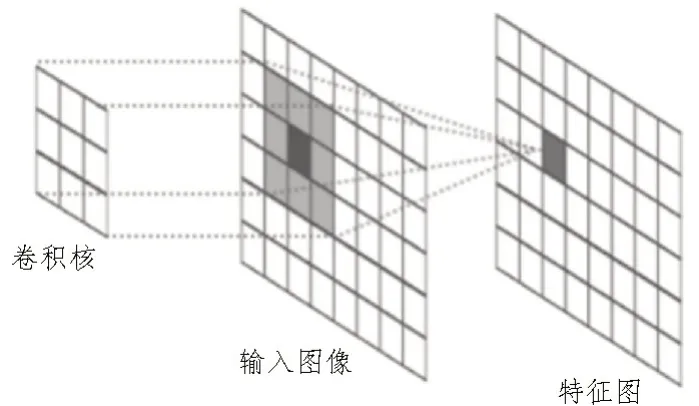
图2 卷积过程示意图

卷积的本质为两个矩阵对应位置上的数据相乘之后再将所有结果相加求和的过程。每一个卷积核与原图像进行卷积后得到相应的卷积结果，即对应的特征图，根据不同的卷积核元素可以获得图像不同方面的特征。在模型训练开始前，通常需要指定卷积核的数量、尺寸、滑动步长以及卷积层的数量等参数。卷积核数量越多，提取的图像特征就越多，神经网络识别能力通常也越强。

整个卷积层的数学表达式如式（1）所示：

其中，*代表卷积运算，Mj代表神经元输入特征图的集合，表示第l-1 层第i个神经元的输入，为第l层卷积核，为第l层第j个神经元的偏置，f(·)为非线性函数则为第l层卷积后第j个神经元输出。卷积结束后，针对每一幅特征图都需要通过某种激活函数来引入非线性特性，式（1）中的f(·)即起到该作用。引入非线性特性的函数通常包括tanh 或sigmoid，对于手写数字识别，用的更多方法的是ReLU，其操作较为简单，且效果较好，实现的思路是将特征图中所有负值调整为0，而正值保持不变，对应的公式如式（2）所示：

式中，为第l层第j个神经元的卷积输出，代表第l层卷积后第j个神经元对应的非线性处理输出。经过非线性处理后的结果进入池化层进行后续的处理。

2）池化层：空间池化也称为子采样或降采样，池化层主要用于减小每个特征图的尺寸，并保留最重要的特征信息。其实现思路：将卷积层输出的特征图划分为多个小块区域，每个区域中用一个值代表该区域内的多个值，获得各个区域代表值的方法可以有多种，如选取区域的最大值、计算区域平均值、计算区域所有值的总和等，计算区域平均值的降采样过程可表示为：

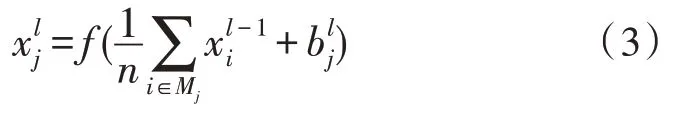
式中，n表示划分的降采样区域中元素的个数，表示第j个神经元的输出，是上一个卷积层中第i个神经元的输入。降采样层每个区域通常取2×2 大小的窗口，即有4 个元素。经过池化处理后只保留该区域的平均值，因此特征图的尺寸会缩小为原来的四分之一。在建模过程中通常可根据需要设置多对卷积层和池化层。

3）全连接层：全连接层是一个传统的多层神经元感知器，该层中的每一个神经元都与上一层的所有神经元相连，并且每个神经元都有一组对应的权重与上一层神经元的输出结果结合，可计算得到当前层神经元的输出，其计算表达式为:

式中，表示全连接层中第j个神经元的权重系数，xl-1表示上一层中神经元对应的输出值，表示全连接层中第j个神经元的偏置量。

为了保证全连接层面向输出层的所有分类结果概率之和为1，可使用Softmax[15]作为全连接层、输出层的激活函数，该函数能接受任意实值分数，并将其压缩为0 到1 之间的值。Softmax 函数得到的结果即为每个样本的分类概率，模型将按照概率值的大小来预测其所属类别。

1.3 卷积神经网络模型训练

在卷积神经网络模型训练之初，其分类误差较大，为了降低误差，通常使用反向传播算法[16]反向调整卷积层中所有卷积核的值以及全连接层中各神经元的权重值，调整的比例与权重值对误差的贡献大小正相关，经过反向调整后的值可使下一次前向传播的分类误差变得更小。

通过前向传播与反向传播算法的多次迭代，可以逐渐将神经网络中各项权值调整至某种状态，使分类结果误差不断减小并趋于稳定状态，训练迭代的次数通常与模型的设计以及准确率的收敛速度有关[17]。可以使用训练好的神经网络对未训练过的新图像进行识别及分类，其分类过程就是对输入的新图像进行前向传播处理，并最终输出对应的分类概率。

2 算法实现

2.1 模型训练

文中采用LeNet-5 模型进行训练，它是一种典型的卷积神经网络模型，主要用于手写体汉字和印刷体汉字的识别。该模型共有7 层（不包含输入层），其中包含2 个卷积层、2 个池化层以及3 个全连接层，每层都包含有不同数量的参数。模型输入层图片大小为32×32 像素。第一个和第二个卷积层分别有32 个、64 个5×5 的卷积核，相应的卷积核滑动步长为1。池化层降采样区域大小为2×2，全连接层中包含256 个神经元节点，激活函数为ReLU 函数，在输出分类结果前通过Softmax 将维度降到10维，分别对应10 个分类结果。

采用Minist 数据集对模型进行训练，该数据集包含55 000 个训练集样本、5 000 个验证集样本以及10 000个测试集样本，每个样本都为二值化图像数据，像素为28×28，而LeNet-5 网络输入图像的像素为32×32，因此训练前需要将Minist数据集中的各个实例填充为32×32。数据集中的样本实例如图3所示。

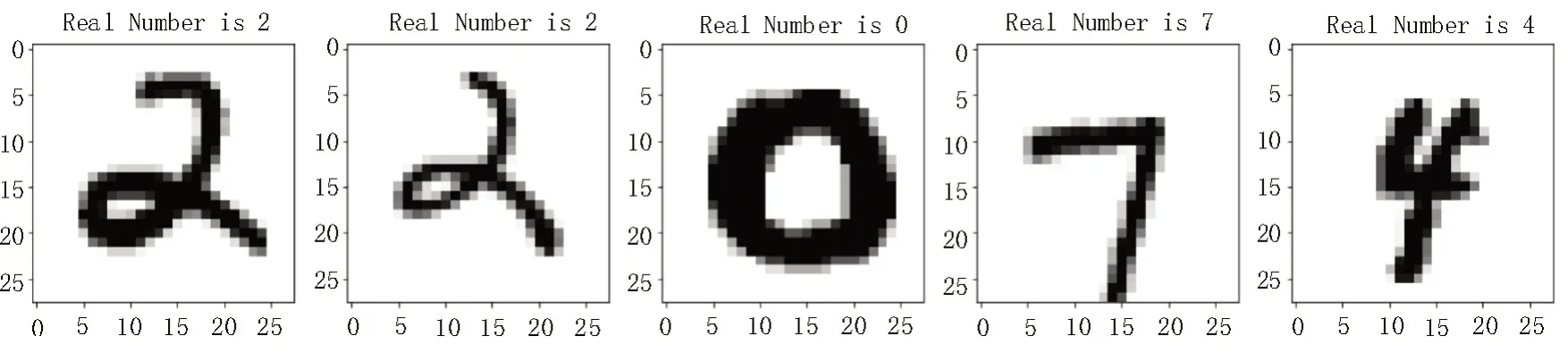
图3 Minist数据集样本实例

在实验中，利用Tensorflow 搭建上述模型进行训练，迭代次数为50 次。为防止训练过程中出现过拟合，还需要设置dropout 概率为0.25，用Softmax 作为分类器，以交叉熵函数作为误差函数训练网络模型，训练的同时通过验证集数据对模型进行验证，得到对应的训练集与验证集的误差对比曲线和识别率对比曲线，分别如图4 和图5 所示。

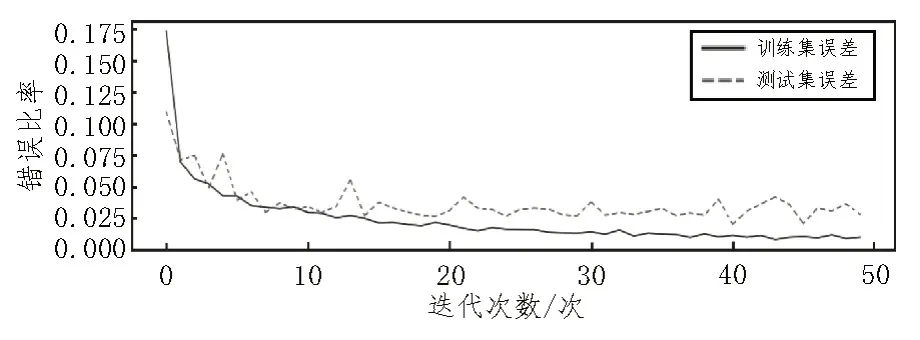
图4 训练集与测试集的误差曲线

图5 训练集与测试集的识别率曲线

由两组曲线图可以看出，整个模型训练过程收敛速度较快，虽然测试集的识别率曲线略低于训练集，但最终识别率均在98%以上，达到了预期的训练效果。

2.2 字符分割

在对手写字体进行识别前，还需要将一幅图中所有手写数字进行阈值和字符分割，使图像中的文字与背景具有足够的区分度，以便后期对每个数字进行独立识别。文中采用自适应二值化方法实现阈值分割，分割前后图像对比如图6 所示。

图6 阈值分割对比图

阈值分割完成后，还需要对单个字符进行提取，文中采用基于方向投影的改进算法对单个字符进行分割，分割后用框线标记出每个字符所在区域。分割结果及样例如图7 所示。

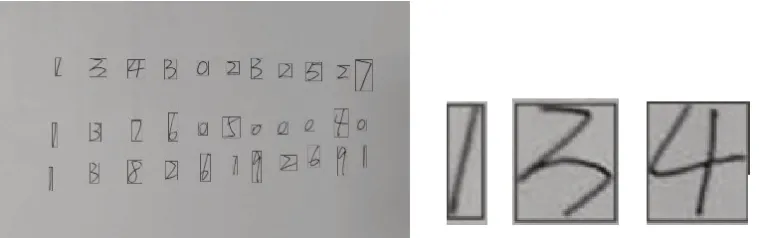
图7 单个字符分割结果及样例

由于前期采用LeNet-5 网络模型进行训练，因此还要使分割得到的图像与模型训练输入的图像格式保持一致，把每个分割出的数字图像像素调整为32×32，同时使手写数字处于图像中间位置，对应的结果示例如图8 所示。

图8 样例字符分割结果

2.3 数字识别

在模型训练和字符分割完成后，可将分割好的字符输入到网络模型中进行分类处理，并根据模型输出层各分类项的概率大小确定最终的识别结果。在实验中将识别结果输出在手写字符的左上方，最终的识别结果如图9 所示。从该图中可以看出，虽然3、4、6 等手写数字有不同的书写风格，但是训练后的模型依然实现了图中数字的正确识别，达到较好的识别效果。

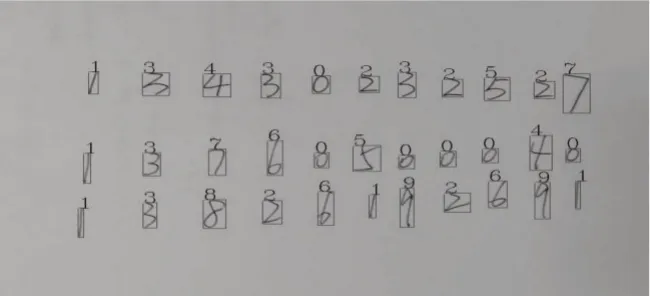
图9 手写数字识别结果

3 实验结果与分析

实验环境操作系统为Windows10，CPU 为intel（R）Core（TM）i7-10750H，内存为16 GB，配置NVIDA RTX 2080ti GPU，在Pycharm 编译器上完成模型训练。启用GPU 并行计算加速后，训练时间为969 s，训练模型对验证集的识别准确率约为98%，但是在后期的模型测试中，依然存在误识别的情况，这种现象在手写数字出现连写或者单个数字手写笔画不连贯时尤其明显。

从后期模型验证的情况可以看出，对于结构较为简单的数字，如0、1 等识别正确率较高；而对于相似度较高的数字，如1、7、9，在书写不规范的情况下依然会出现错误识别。此外，对于连写数字，由于在预处理过程中，文中方法无法将其分割开，因此相关识别结果都出现了错误。对于该类情况，下一步要重点研究连写数字的分割方法，并扩大连写数字的训练数据集，以此提升模型的适用范围和多种情况下的识别率。在实验的最后，选取了不同人员书写的0-9 数字各100 个对模型的识别率进行了测试，相关识别结果统计如表1 所示。

表1 识别结果统计

4 结论

文中基于卷积神经网络基本原理，通过Tensorflow搭建手写数字识别训练模型，较好地实现了单幅图像多个数字的正确识别，为理解CNN 的相关原理和实现过程提供了参考。通过多个实验测试发现，对于单幅图内多个手写数字的识别，除了搭建稳定的训练模型外，还需要对输入图像进行较好的预处理和预分割，在此基础上进一步扩大CNN 模型训练集的范围，采集不同行业以及不同年龄段的手写数字样本对模型进行训练，以使训练模型具备更高的识别率和实用性。