基于图像边缘轮廓的角点检测算法研究

蒋延杰，谢蓉蓉，李云红，何亚瑞，陈锦妮

（1.北京市组织机构代码管理中心，北京 100010；2.西安工程大学电子信息学院，陕西西安 710048）

角点包含图像重要的结构信息，其应用遍及图像匹配[1]、目标识别与追踪[2]、3D 目标重建[3]等众多领域。为提高角点检测精度，降低计算复杂度，角点检测算法被研究者不断提出。角点检测算法根据实现方法的不同可分为三类[4-8]：基于角点模型的方法、基于灰度强度的方法和基于边缘轮廓的方法。

Wang[9]等人提出了基于迭代阈值的自适应Harris角点检测算法，解决了在提取角点时必须给出合适阈值的问题，但对噪声图像角点的提取不准确。高华[10]提出了一种基于Log-Gabor 梯度方向一致性的角点检测算法，用来提高角点检测器的检测性能，但其鲁棒性有待提高。使用各向异性高斯方向导数滤波器，可以提高噪声鲁棒性和定位准确性[11]。Cho[12]等人提出了一种基于非角度测量的角点检测方法，消除了位于平坦区域的像素并删除了任意方向沿边缘的像素，但计算复杂度高。

相比较，该文所提算法以点到弦之间的欧氏距离为基础，不用计算任何导数，对于局部变化也具有鲁棒性。

1 角点检测算法

基于图像边缘的角点检测器基本使用曲率技术对角点进行检测，基于曲率尺度空间（CSS）的角点检测算法[13]存在两个主要问题。首先，由于曲率的定义是曲线上角度的瞬时变化率，因此对局部变化和噪声非常敏感，进而会产生误检。其次，对于高斯平滑尺度的选择，针对这类角点检测算法的不足，该文提出一种新的角点检测算法。图1 是该文算法的流程图。

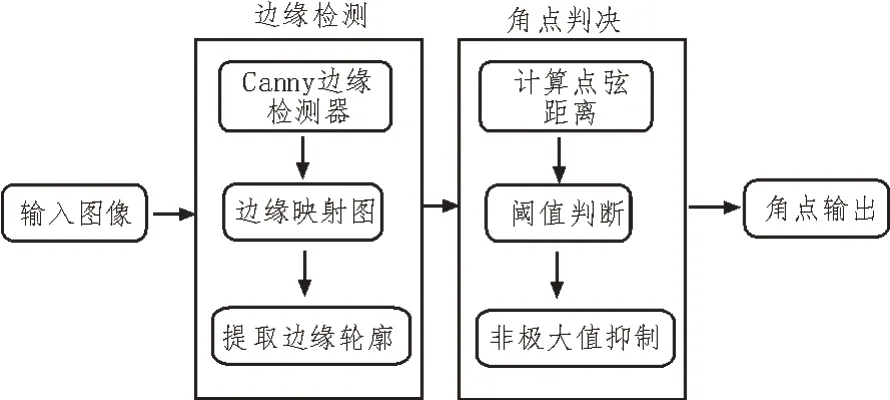
图1 算法流程图

1.1 边缘检测

首先使用Canny[14]边缘检测器提取图像的边缘轮廓。边缘像素被定义为两侧的梯度大小都小于像素本身梯度大小的像素。Canny 边缘检测算法主要包括以下四步：1）使用高斯滤波器对原始图象进行平滑处理；2）使用一阶偏导的有限差分对图像梯度的幅值和方向进行计算；3)对梯度幅值进行非极大值抑制；4）使用双阈值算法对边缘进行检测和连接。

该文采用的角点检测算法中将Canny 边缘检测器的阈值设定为[0.2,0.35]。当从原始图像中提取边缘线时，所提取的边缘线之间可能有小的间隙，而这些间隙中可能存在角点。因此，在角点检测前填充轮廓线间的间隙是非常重要的，可以避免真实角点的丢失。图2 是‘Lenal’图像的边缘映射图。

图2 ‘Lenal’图像的边缘映射图

1.2 角点判决

从边缘映射图中提取出的每条边缘线，通过连接边缘线首端和尾端得到一段弦，找到边缘线像素点与弦之间的最大欧氏距离[15]。如果距离大于最佳阈值，那么对应于边缘线上的点就被认为是一个候选角点。由于该文所提算法在平移和旋转，统一和非统一比例缩放的几何变换中是不变的，因此，当任何一个边缘线发生几何变换时，边缘线上任意一个像素点与弦之间的距离不会发生改变。图3 针对‘house’图像进行了伪角点的去除。

图3 ‘house’图像伪角点的去除

2 实验结果分析

为了验证所提基于图像边缘角点检测算法的有效性，将角点检测器的平均可重复性和定位误差作为研究性能指标。通过对所提检测算法与Harris、He&Yung 和CPDA 三种经典检测算法的比较进行性能评价。为了进行公平的比较，在实验过程中，所有的角点检测器均使用相同的边缘线提取和轮廓线选择方法。

2.1 数据变换

为了评估四种角点检测算法的检测性能，从标准数据集[16]中选取图像。从数据集中选取的每幅图像均经过六种不同的转换方式进行变换。

1）旋转变换：采用18 个不同角度进行变换，每次以10°为步长，在[-90°,90°]范围内进行旋转变换；

2）统一缩放：尺度因子Sx=Sy，每次以0.1 的增量在[0.5,2.0]范围内进行统一缩放；

3）非统一缩放：尺度因子Sx=1，Sy每次以0.1的增量在[0.5,2.0]范围内进行非统一缩放；

4）剪切变换：剪切因子c在[-1,1]范围以0.1 的增量调节进行变换；

5）JPEG 质量压缩：质量因子在[5,100]的范围以5%增量调节进行压缩变换；

6）高斯噪声：零均值高斯白噪声标准差每次以1的增量在[1,15]范围内进行增加。

2.2 评价准则

原始测试图像和转换后的图像之间在同一位置检测到角点的平均数称为平均可重复性，用Ravg表示。对于给定变换下的角点检测器，每幅测试图像的平均可重复性被定义为：

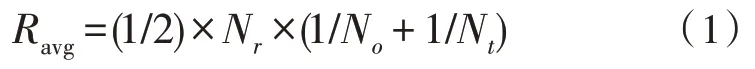
在式（1）中，No表示原始测试图像中角点的数目，Nt表示转换后图像中角点的数目，Nr表示原始测试图像和转换后图像之间重合的角点数目。

原始测试图像中检测到的角点和转换后的图像中检测到的相对应角点之间的平均距离称为定位误差，用Le表示。表示原始测试图像与转换后测试图像所对应的角点对。则定位误差可表示为：

2.3 实验结果对比

对标准数据集进行旋转、剪切、高斯噪声、质量压缩、统一及非统一缩放六种数据变换，四种角点检测算法的平均重复性和定位误差等性能比较的实验结果如图4所示。在旋转变换下，He&Yung角点检测算法的平均重复性最高。CPDA 角点检测算法和所提算法的定位误差比较低。在统一缩放和非统一缩放变换下，所提算法与CPDA 角点检测算法相比，实验最终检测结果相差不大，均获得了较好的检测结果；而He&Yung 角点检测算法与Harris 角点检测算法的检测结果与前两种相比略显不足。但是在高斯噪声条件下，所提算法在定位误差和平均重复性上性能最好。

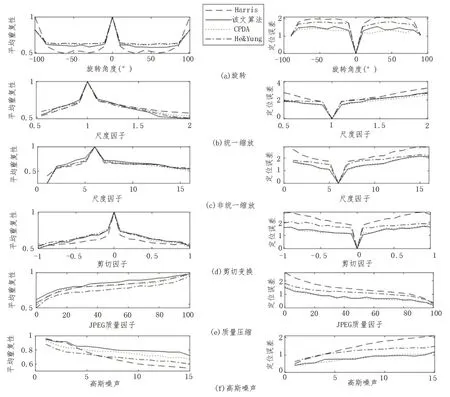
图4 在六种不同变换下的平均重复性和定位误差

之后，选用图像处理中普遍使用的灰度图像‘Block’，测试其分别在无噪声和有噪声情况下的检测结果。图5 是‘Block’图像的四种角点检测算法的检测结果。观察图5 可以看出，该文所提算法相比于其他三种检测算法的检测结果相对较好。图6 是带噪声的‘Block’图像的四种角点检测算法的检测结果，添加了方差为10 的高斯白噪声，可以看出所提算法同样具有较好的检测性能。

图5 ‘Block’图像的检测结果

图6 带噪声的‘Block’图像检测结果

3 结论

该文提出了一种新的基于图像边缘轮廓的角点检测算法，该角点检测算法不需要通过曲率计算就能获取候选角点，该算法与CPDA 角点检测方法完全不同，既不需要通过移动的弦长去累加曲线上弦点之间的每一段距离，也不必通过三个不同长度的弦长来计算曲线上每一点的归一化曲率值。因此，在保持良好的平均可重复性和准确性时也能加快检测的速度。通过实验测试可以得出，该文所提角点检测算法相比于其他三种经典的检测算法具有更好的检测性能。