自升式风电安装平台插销式桁架桩腿仿真与分析*

贾 森 刘鹏飞 刘安琴

1烟台理工学院 烟台 264000 2烟台中集来福士海洋工程有限公司 烟台 264012

0 引言

随着全球环境污染及能源紧缺问题的日趋严重，人类对能源需求量的日益增加陆地能源的日渐枯竭,世界各国对海洋资源越来越重视，加紧了对海洋资源的开发利用[1]。风能作为一种可再生无污染能源，其发展越来越受到重视。在各种海洋平台中，自升式风电安装平台适用于浅海海区，具有用钢量少、造价低、在各种海况下几乎都能持续工作且效率较高等优点[2]。然而，自升式风电安装平台桩腿长度有限，使其工作水深受到限制。最大工作水深约550 ft，超过此水深桩腿质量增加很快，水下受到波浪相应也会增大，同时拖航时桩腿升起很高，对桩腿强度和平台稳性很不利。本文通过系列的计算，总结出桩腿各构件对桩腿强度的贡献规律，从而为桩腿优化设计起到一定指导意义。

1 自升式风电安装平台的桩腿结构

自升式风电安装平台按桩腿数量分有3腿、4腿、5腿[3]。3腿自升式风电安装平台具有更加优越的稳性，目前全球的3腿自升式钻井平台占全部自升式风电安装平台总量的80%以上。按桩腿的形式自生式风电安装平台常见的桩腿结构形式分为壳体式和桁架式2种，壳体式桩腿制造简单，以插销式为主，插销式壳体无需焊接齿条，但其钢结构利用率低，经济性能不好，波浪载荷大，同等承载能力下需要更多的钢结构，且仅适用于浅水域。一般工作水深在250 ft以下，再深则需增大桩腿尺寸，由此会导致更大的波浪载荷，结构质量也会增加。桁架式桩腿钢结构利用率高，波浪载荷小，可适用于较深海域，但制作要求高，尤其齿条的焊接和安装难度较大，故250～550 ft水深的自升式风电安装平台一般采用桁架式结构。综合2种桩腿优缺点，采用插销桁架式桩腿，主弦管同截面设置2个插销孔。

桁架式桩腿按照弦杆数量分有3弦杆和4弦杆式，典型的3弦杆桁架式桩腿结构如图1所示。

图1 典型桩腿结构图

桁架式桩腿由主弦杆、斜撑杆、水平撑杆、内水平撑等组成，在弦杆上有插销空，供插销式液压升降机构把平台主体进行升降。

2 不同结构形式桩腿的等效几何性质

自升式风电安装平台主船体的刚度比桩腿的刚度要大得多，且由桩腿受力情况可知，桩腿为压弯构件，其强度相对于船体而言是薄弱构件[4]，故桩腿整体强度计算是必不可少的。

由于插销桁架式桩腿被理想化为相当杆件，应先要求得其相当杆件的截面几何性质。常见的桩腿侧面形式如图2所示。

图2中3种形式的桁架式桩腿的侧面等效剪切面积AQ分别为

图2 不同形式桩腿等效剪切面积示意图

整个桁架式桩腿的截面几何性质计算为

式中：A为桩腿截面面积；AQy、AQz为桩腿在y、z方向的等效剪切面积，即桩腿抗剪切能力；Iy、Iz为桩腿对y、z轴的惯性矩，即桩腿抗弯能力；IT为桩腿截面扭转惯性矩，即桩腿抗扭能力；ν为材料泊松比。

3 桩腿各构件对桩腿强度的影响

3.1 有限元模型

该自升式风电安装平台的主体为三角形箱形结构，有3条插销式桁架式桩腿，桩腿为K形结构，每条腿有3根主弦杆，根据平台特点，平台主体和桩腿均用杆单元进行模拟[5]。计算模型如图3所示，坐标原点位于前桩靴基线与桩腿轴线交点处，X轴正向指向平台艏部，Y轴正向指向平台左舷，Z轴正向竖直向上。

图3 计算模型

在图3中，模型A根据ABS规范将桩腿简化为一根等效梁[6]，建立不同节距高度及不同弦杆间距的模型，来计算桩腿的整体强度，不同节距高度和弦杆间距的等效梁尺寸如表1、表2所示。

表1 不同节距高度的等效梁尺寸

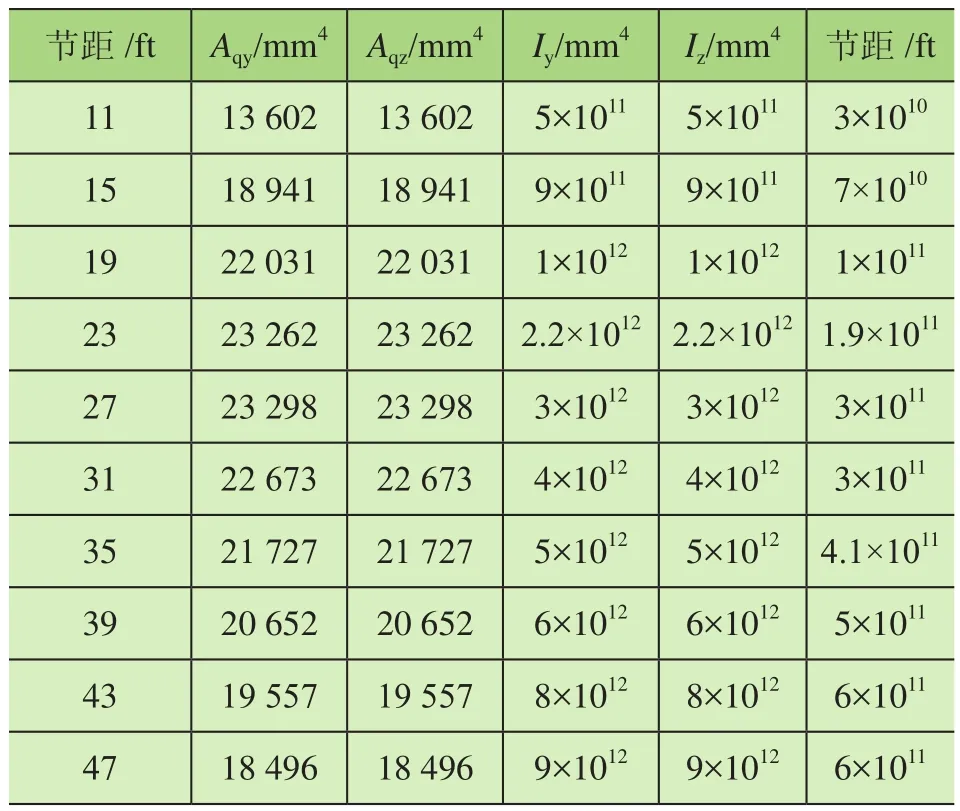
表2 不同水平撑长度的等效梁尺寸

模型B平台主体和桩腿上的杆件都用杆单元模拟，建立一系列不同弦杆、斜撑和水平撑杆壁厚的模型，计算桩腿的强度，不同斜撑、水平撑和弦杆壁厚尺寸如表3、表4所示。

表3 不同斜撑和水平撑的尺寸 mm

表4 不同弦杆的尺寸 mm

在桩腿的强度计算中，每个桩腿主弦管上插入的圆柱销共同承担载荷。圆柱销插入主弦管如图4所示。

图4 插销插入主弦管示意图

3.2 边界条件

自升式风电安装平台在风暴自存工况下桩腿所受的外力要比正常工作时大，故以风暴自存工况进行计算。边界条件按照ABS规范，取海底泥面下3 m处简支[7]。

3.3 载荷施加

风电安装平台船体被桩腿支撑在海面之上时，船体上的甲板载荷和风载将通过桩腿传到海底，这时桩腿受到风力、波浪力、潮流力、平台的重力及功能性载荷、惯性力和P -Δ二次弯矩等的影响。在风暴自存工况下，平台一般处于不工作状态，这时压载舱会打入压载，作业机构收回。这时的重力载荷包括空船质量、可变载荷、固定载荷，这些载荷都会以点载荷方式施加在平台主体梁上，由静力等效原理，风载、惯性载荷、P -Δ载荷均可转化为力与弯矩之和，以力和弯矩的形式施加。环境载荷包括风、浪、流引起的载荷。

3.4 桩腿强度校核

对于承受轴向压缩和弯曲载荷共同作用的构件，ABS规范给出其压缩应力和弯曲应力应满足

当fa/Fa≤0.15时，压缩应力和弯曲应力应该满足

式中：fa为计算轴向压应力，Fa为计算轴向临界应力，Cmx、Cmy为x轴、y轴的修正系数，fbx、fby为x轴、y轴的计算弯曲应力，Fbx、Fby为x轴、y轴的许用弯曲应力，F＇ex、F＇ey为x轴、y轴的欧拉应力。

3.5 桩腿各构件对桩腿强度的影响规律

根据风暴自存工况下平台所受载荷，计算平台的强度依据AISC规范对桩腿结构进行强度评估，计算结果如图5所示，平台桩腿受到的弯矩剪力如图6所示[8]。

图5 风暴自存工况下平台计算结果

图6 风暴自存工况下平台桩腿剪力和弯矩图

由图5、图6可知，桩腿最大的UC值出现在围井区域，向下至桩腿底部逐渐减小。由于斜撑杆是传递水平载荷和弯矩的，使桩腿上弦杆的应力趋于平衡，故其承受了很大的剪切力和弯矩[9]。水平撑杆相对的弱于弦杆，主要承受横向载荷。弦杆的主要作用是抵抗压力和弯矩，根据自升式风电安装平台的受力特征，平台桩腿所受弯矩从桩腿底部到平台主体位置逐渐增加，所以弦杆UC值也是从下到上逐步增加，至围井区域位置达到最大。

计算不同节距高度和不同弦杆距离系列模型的强度，取围井区桩腿同一位置构件在各工况下的最大值，分别得出等效桩腿整体强度的UC值随节距高度和弦杆距离变化的曲线如图7、图8所示。

图7 UC值随桩腿节距高度变化曲线图

图8 UC值随桩腿弦杆距离变化曲线图

由图7可知，当斜撑杆和水平撑杆尺寸不变时，随桩腿节距的增加等效桩腿的UC值先快速下降，在节距高度为15 ft时UC值达到最小值，之后再缓慢上升，说明等效桩腿强度在节距高度为15 ft时最大。由图8中可知，当桩腿节距高度不变时，随着弦杆距离的增加等效桩腿的UC值呈现出标准的二次曲线形式，先下降并当水平撑杆长度在25 ft时UC值达到最小值，而后上升，说明等效桩腿强度在水平撑杆长度为25 ft时最大。

计算不同撑杆和弦杆壁厚的系列模型的强度，取围井区桩腿同一位置构件在各工况下的最大值，分别得出桩腿的UC值随节距高度和弦杆距离变化的变化规律。

当斜撑和水平撑管厚的增加而其他杆件尺寸不变时，随着斜撑和水平撑管厚的增加，弦杆的UC值有所减小，但变化不大。由此，从计算结果中可知，当桩腿强度不够需要修改时，增大撑杆尺寸对弦管强度影响不大。当弦杆壁厚增加而其他杆件尺寸不变时，随着弦杆管厚度的增加，斜撑和水平撑的UC值无显著变化，而弦杆的UC值呈线性下降，但下降斜率不是太大。因此，当桩腿强度不够需要修改时，增大弦杆尺寸对斜撑杆和水平撑杆强度无较大影响，但桩腿质量会增加很多。

4 结论

对某自升式风电安装平台的桁架式桩腿结构，按照ABS船籍社的规范要求，计算了4种不同形式的桩腿抗弯、抗扭、抗剪的利用率，研究了桩腿的不同结构尺寸在风暴自存工况下的综合强度，得出以下结论：

1）随着桩腿节距的高度和弦杆间距变化，桩腿形式B的抗扭、抗剪能力都明显优于其他3种，形式A的次之,形式D的最差，4种形式抗弯能力相差不大。

2）在风暴自存工况下，桩腿最大的UC值出现在围井区域，向下至桩腿底部逐渐减小。水平撑杆相对的弱于弦杆，其主要是承受横向载荷。平台桩腿所受弯矩从桩腿底部到平台主体位置逐渐增加，所以弦杆UC值也是从下到上逐步增加，至平台围井区域位置达到最大。

3）当斜撑杆和水平撑杆尺寸不变时，随着桩腿节距的增加，等效桩腿的UC值先快速下降，当节距高度为15 ft时UC值达到最小值，后再缓慢上升，当桩腿节距高度不变时，随着水平撑杆长度的增加，等效桩腿的UC值呈现出标准的二次曲线形式，先下降并当水平撑杆长度在25 ft时UC值达到最小值，而后上升。

4）增大撑杆壁厚对弦管强度影响不大，增大弦杆尺寸对斜撑杆和水平撑杆强度没有太大影响，但桩腿质量会增加很多。