舰空导弹飞行落点贝叶斯融合预估方法

袁非梦，耿化品，凡红梅，锁 斌

(1.西南交通大学数学学院，四川 成都 611730；2.北京机电工程研究所，北京 100083； 3.西南科技大学信息工程学院，四川 绵阳 621010； 4.西南科技大学复杂环境装备可靠性中心，四川 绵阳 621010)

0 引言

随着舰空导弹武器系统的发展，其作战性能和作战空域不断提高。舰空导弹的落点预报是导弹预警系统中的一个重要环节，落点预报精度是一项非常重要的战技指标[1-2]。实践证明，增大弹头威力和提高导弹的落点精度都将提高导弹的毁伤概率，将导弹的落点精度提高1倍，相当于导弹的威力增大8倍[3]。提高落点预报和误差分析精度具有很强的工程意义，提高落点预报精度的关键是建立准确的预报模型。

近年来针对导弹飞行落点预报问题，诸多学者展开了研究：文献[4]通过对影响导弹落点精度的因素分类和影响分析，提出了利用仿真技术预测和修正弹道导弹落点偏差的方法，综合诸影响因素对导弹进行全弹道仿真实验设计和分析，为改进设计提供了一定的依据；文献[5]在无再入观测数据条件下，基于导弹末端速度变化范围的限制，预估气动阻力参数变化范围，对弹道导弹的落点和气动阻力参数进行了高精度联合预报；文献[6]为评估制导导弹和炮弹的命中精度，提出了一种新的椭圆概率误差的落点精度评定方法，并给出了精确表达式，为预估落点误差的方向性及目标摧毁概率范围提供依据；文献[7]针对靶场舰空导弹飞行试验安全判定的试验需求，分析了一种基于落点预估的舰空导弹飞行试验安全判定方法；文献[8]根据炮射导弹的射击特点，分析了炮射导弹落点精度的概念及其相关指标，提出了评定炮射导弹落点精度的方法。但上述研究均需要大量的导弹真实落点提供数据支撑，对导弹的外场数据样本量和置信度要求较高，而对舰空导弹做大量外场试验，存在设备成本高、布放工程量大、安全隐患等诸多问题。因此考虑借用导弹液压飞行仿真转台模拟导弹飞行控制系统进行仿真试验，模拟导弹在空中飞行时的运动和姿态。液压飞行仿真转台采用电液伺服控制技术，具有控制精度高、响应速度快等优越性，能够积累大量半实物仿真导弹落点数据。

目前，国内外学者针对外场试验、半实物仿真等多源数据的精度融合评估问题开展了较多研究，主要的数据融合方法包括：深度神经网络法[9]、贝叶斯推理[10]、模糊逻辑[11]和D-S证据理论[12]。为了提高多传感器数据融合的精度，文献[13]提出了一种基于BP神经网络的数据融合新算法，可以有效处理网络不收敛问题，提高网络性能；文献[14]通过优化网络输入，提出一种基于粒子群优化的改进反向传播神经网络的多传感器数据融合算法，提高了传感器数据融合的准确性；文献[15—16]提出了一系列基于Bayesian推理的数据融合方法，具有较好的融合效果；文献[17—19]将模糊集理论应用于多传感器数据融合，降低了传感器数据信息的不确定性，且具有较小的计算复杂度；文献[20—21]采用D-S证据理论进行多源数据融合，减小了对先验知识的依赖性，且采用单周期的融合方式融合性能较好。其中，对于具有高可靠性和少量外场数据的装备，Bayesian融合方法可以充分利用验前的仿真试验信息和现场试验数据，得到了较多学者的关注。文献[22]研究了运用Bayesian理论从仿真实验数据中提取有用信息，从而实现在少量现场试验样本情况下有效完成试验鉴定任务的方法；文献[23]讨论了一种基于Bayesian理论的滤波方法，用于提高导弹射击精度鉴定的抗噪声和抗干扰性能；文献[24]通过分析数据融合的结构，重点研究了基于遗传算法的分布式Bayesian融合系统的全局优化，建立了全局最优的Bayesian融合检测系统；文献[25]针对轴向柱塞泵故障特征的模糊性和不完备性，提出了一种Bayesian网络与多特征信息融合的方法，并验证了该方法能够有效实现柱塞泵的故障诊断。上述研究成果都充分展现了Bayesian融合方法的优越性和有效性，Bayesian融合方法在现场试验数据较少的小样本场合应用十分广泛，在多源数据的精度融合评估中效果较好。

因此，研究在只有少量外场数据和较多的半实物仿真数据情况下的舰空导弹落点预估问题时，Bayesian融合方法展现了良好的优势。Bayesian融合技术能有效处理小子样问题，将该技术用到导弹落点预估问题上，可以融合导弹的先验半实物仿真数据信息和外场落点数据信息，进而动态修正并预测导弹的落点坐标。基于这种思想，本文针对舰空导弹的落点预测问题，提出基于Bayesian多源数据融合的舰空导弹飞行落点预估方法。采用导弹飞行仿真技术得到大量半实物仿真落点数据，将导弹落点坐标的半实物仿真数据和外场试验数据有效融合，计算机自动化处理出若干预示落点，再结合人工经验预测导弹落点。

1 Bayesian数据融合原理

Bayesian理论基本原理是：给定某假设的先验似然估计，随着新的证据(观测数据)的到来，Bayesian方法可以更新假设的似然函数。Bayesian方法解决统计问题的思路不同于经典统计方法，它的一个显著特点就是在保证决策风险尽可能小的情况下，尽量应用所有可能的信息。这不仅仅是外场试验的信息，还包括外场试验之前的信息，如导弹系统在研制中的有用信息、仿真实验的信息、同类武器装备系统的试验信息，而真正的外场试验数可以是少量的。因此，在上述先验信息存在的情况下，作为一种数据融合方法，Bayesian方法可以用于小子样试验分析。

观测样本X=(X1,X2,…,Xn)为总体样本，X的密度函数为p(x;θ)，θ为待估参数。Bayesian学派将θ与X同样看作随机变量，将经典统计中的p(x;θ)看成条件概率密度p(x|θ)。在先验分布π(θ)下，对θ产生新的认识，求出后验密度：

(1)

式(1)中，π(θ)为先验分布，pX(x1,x2,…,xn|θ)为样本的极大似然函数，θ的分布类型仅由π(θ)pX(x1,x2,…,xn|θ)决定，因此，Bayesian统计模型可以简化为h(θ|x)∝π(θ)pX(x|θ)。

对于具有大量半实物仿真导弹落点信息和少量外场试验信息的情况，将仿真数据作为先验信息，外场数据作为现场子样，借助Bayesian理论即可实现落点数据的融合。

2 基于Bayesian方法的半实物仿真与外场数据融合

导弹的外场试验数据与半实物仿真数据的多源融合评估流程如图1所示。

图1 多数据源融合评估流程图Fig.1 Flow chart of multi-data source fusion assessment

2.1 基于概率分布特征和代理模型的外场试验数据扩充

2.1.1基本概率分配函数的构造

基本概率分配是证据理论中的一个重要概念，证据理论一般是指Dempster-Shafer(D-S)证据理论[26]，最先由Dempster提出。它为决策不确定信息的表征与融合提供强有力的工具，在相关领域展现出良好的应用效果[27-28]。对于一个问题而言，设研究对象x在集合Θ={θ1,θ2,…,θN}内取值，其中Θ为一个两两互斥的完备集合，称Θ为x的辨识框架。

基本概率分配(basic probability assignment, BPA)是证据理论中最基本的信息载体，它表示证据支持命题的信任程度m：2θ→[0,1]，且满足

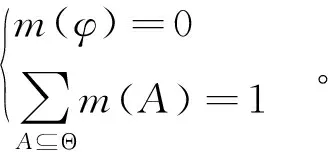
(2)

若m(A)>0，则称A为m的焦元(focal element)。

表示信任分配与赋值支持的基本概率函数BPA的获取是确定各区间需要生成多少样本点的关键。BPA的获取可以由决策者或专家根据主观经验给出，也可以根据系统的性质利用模糊理论和粗糙集理论等进行 mass 函数的构造。由于信息类型的多变性，即使在一个系统内部的BPA计算方法也不一定能够统一，即BPA的获取方法要根据系统数据的具体情况而定。

本文提出一种基于皮尔逊相关系数改进D-S证据理论中BPA的构造方法。考虑到实际完备的识别框架Θ={θ1,θ2,…,θn}中，各证据存在着相关关系，所以不同证据体对于命题的评估差异必然引起证据体在识别框架中的权重比例。因此，通过皮尔逊相关性系数计算和分配各个证据体的整体权重比例是决定外场数据在每个分隔区间扩充多少样本点的重点。

对证据体θ1和证据体θ2计算皮尔逊相关性系数ρ12的计算式为

(3)

式(3)中，cov表示协方差；E表示数学期望；μmi和σmi的计算式分别为

(4)

多证据体的情况下，相互计算两两证据体之间的相关性系数，并构成证据体相关性矩阵：

(5)

由于皮尔逊相关系数的值域为[-1,1]，负值表示负相关，负值越小说明负相关程度越高。为了控制非正相关的证据体在识别框架中的权值比重和可信度计算，以及考虑克服组合规则中的0置信问题和尽量减少对于整体识别框架的基本概率影响，这里将相关性结果小于0的赋值为其相反数，将等于0的赋值为0.001。

通过相关系数和数据概率特征相结合的准则来确定数据之间相似度构造BPA的方法，同时考虑了数据间的相关性与分布特征。皮尔逊相关系数能够反映外场试验数据之间的相似性：相关系数的绝对值越大，相似性就大；相关系数的绝对值越小，相似性就小。本文外场试验数据之间相似度的计算方法具体步骤如下：

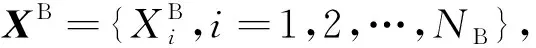
(6)

C序列可构成由NB-1个区间数组成的集合CI：

(7)

根据定义2中的计算方法，计算皮尔逊相关系数有

(8)

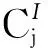
(9)

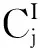
(10)

2.1.2外场试验数据的扩充

(11)

这种以基本概率分配为依据的样本扩充方法可以保证扩充后的样本依然保留原有的概率特征，且不增加人为假设。

1)半实物仿真系统代理模型的构建

基于BP神经网络建立半实物仿真系统代理模型，神经网络是由神经元按规则排列后相互连接而构成的一种非线性动力学系统，其特点在于信息的分布储存和协同处理，单个神经元结构很简单、功能有限，但是由神经元构成的网络系统所能实现的功能却很强大。不仅具有计算功能和自学习能力，并且具有容错性和鲁棒性，善于联想和综合推理。

在学习过程中，半实物仿真系统的输入数据由输入层输入，由隐含层处理之后将结果传向输出层。如果结果和实际半实物仿真系统输出不符合，则将误差逆向传播到隐含层，修改相应的权值和阈值。学习过程结束后，则进入验证阶段，将外场试验条件输入，根据神经网络得出的外场落点结果与实际情况比较，并对模型进行修正。外场试验条件主要包括发射条件和环境条件。发射条件包括高度、速度、三个方向的姿态角(x、y、z轴方向)；环境条件包括温度、风速、风向等其他干扰。输出数据则是x、y、z轴三个方向的落点坐标。

图2为一个具有d个输入和n个输出的BP神经网络模型。图中x1,x2,…,xd为神经元的输入向量；y1,y2,…,ym为隐含层神经元输出向量；vih,whj分别为输入层权值链接、隐含层权值链接；am为隐含层神经元的偏置；o1,o2,…,on为输出层的输出；bn为输出层神经元偏置；激励函数φ为S型传递函数。

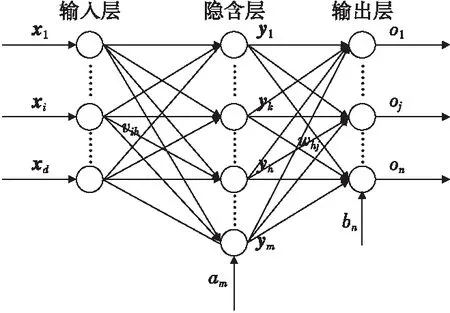
图2 BP神经网络模型示意图Fig.2 Schematic diagram of BP neural network model

基于BP神经网络方法构建的半实物仿真系统代理模型，能够生成大量半实物仿真的落点坐标数据，且借助于BP神经网络方法，不仅能够有效避免数据分散性、分布模型选取失误导致的评估误差，而且扩充数据样本与原始数据样本的变化规律基本相同，可作为外场试验落点坐标数据扩充的参考数据。

2)外场落点坐标数据的扩充

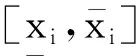
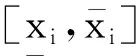
2.2 基于Bayesian方法的半实物仿真与外场数据融合

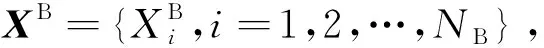
(12)

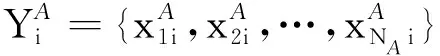
(13)

(14)

3 算例分析

以某舰空导弹发射10次的落点数据为例，将导弹第一次向空中击中点的坐标记为原点(0,0,0)，建立空间直角坐标系。x,y,z分别表示三个方向的坐标轴数据，且取前、右、上分别为三个坐标轴的正方向。取落点的半实物仿真数据样本量为NA=50，外场试验数据如表1，样本量为NB=10。

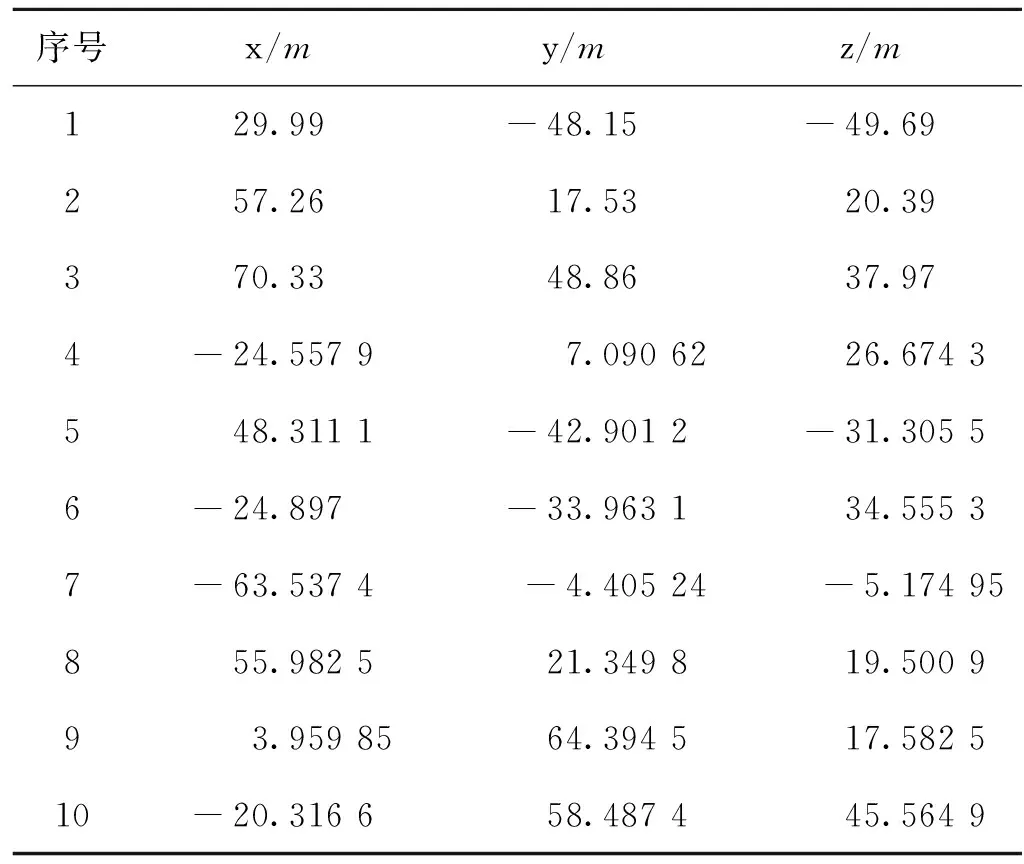
表1 外场落点坐标数据Tab.1 Coordinate data of the outfield landing point

以外场试验数据中的x轴方向坐标为基准，有

XB={-63.537 4 -24.89 7 -24.557 9 -20.316 63.959 9 29.99 48.311 1 55.982 5 57.26}。

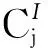
P={0.223 7 0.179 2 0.174 0 0.142 4
0.095 6 0.062 6 0.046 7 0.041 8 0.033 9}，

并确定需要在划分区间

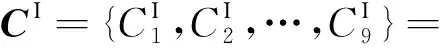
扩充的样本量个数分别为9,7,7,6,4,3,2,2,0。

根据构建的半实物仿真系统代理模型，以第一个划分区间[-63.537 4,-24.897]为例，以属于该区间的x轴坐标数据为基准，绘制直方图。在该区间[-63.537 4,-24.897]需要扩充的样本量个数为9，因此选择直方图中取值概率最高对应的数据作为样本点，分别为{-42.47,-43.158 8,-41.781 2,-43.847 7,-41.092 3,-44.536 5,-40.403 5,-45.225 3,-39.714 7}。

将上述样本点按照从小到大的次序进行排列，填入小区间内实现扩充。采用同样方法对相应的y轴坐标和z轴坐标处理，得到该区间需要扩充的三维落点坐标样本点，同样对其他小区间做此处理，得到样本量扩充到与半实物仿真数据相等的外场落点坐标。

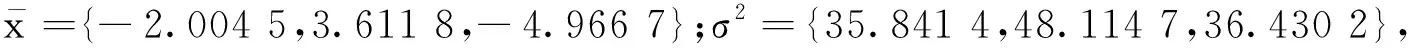
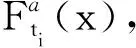
(15)

从式(15)可知，当融合后数据与真实落点数据的概率分布越接近时，面积度量指标越小，反之越大。因此，面积度量指标可以表征外场数据与半实物仿真数据融合效果的好坏。绘制累积分布函数图如图3所示。

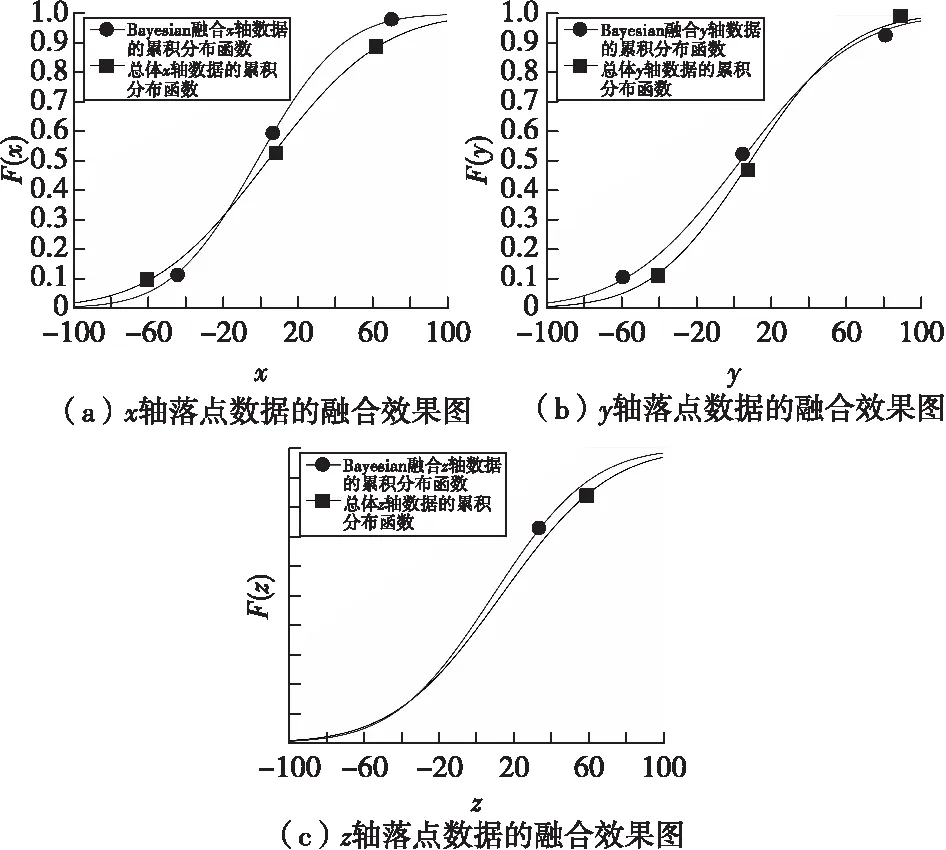
图3 基于Bayesian融合的导弹飞行落点融合效果图Fig.3 Fusion effect of missile flight landing point based on Bayesian fusion

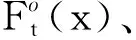
采用K-S假设检验对基于Bayesian融合后的导弹落点和总体的真实导弹落点数据进行同分布检验，计算得p=0.000≪0.05。由此，可以认为在5%的显著性水平下，二者为同分布类型。综合面积度量指标和假设检验结果，验证我们所提出的导弹外场试验数据扩充方法对数据融合是有效的，Bayesian融合方法也是有效的。

4 结论

针对在少量外场试验数据的条件下需要对舰空导弹落点进行预估的问题，本文提出一种利用基本概率分配函数、构建半实物仿真系统代理模型、借助经典Bayesian理论的小样本扩充和Bayesian融合方法。通过这种方法预估的导弹落点坐标更加精准，预测效果更好。通过分析得到以下结论。

1) 采用D-S证据理论中的基本概率分配概念，基于外场数据间的相关系数确定每个小区间需要扩充的样本个数，保留了原始数据的概率分布特征。

2) 基于BP神经网络方法构建半实物仿真系统代理模型生成落点坐标数据集，再采用直方图统计方法依据样本概率大小确定增补的样本点，保证了增补的导弹落点坐标具有物理内涵。这是由BP神经网络模型本身的特性决定的。一方面BP神经网络能避免原始数据分散性、分布模型选取失误导致的评估误差；另一方面，半实物仿真样本与原始数据样本的变化规律基本相同，可作为外场落点的参考数据。

3) 通过对原始样本的扩充重构，增加了外场落点样本的信息量。基于Bayesian融合方法，将半实物仿真数据作为先验信息，提升了导弹落点坐标融合模型的准确性。通过某舰空导弹实物的外场和半实物仿真试验的研究，验证了该方法的有效性。