基于冲击电流发生器的强电磁环境模拟试验方法

康婉玉，刘 星，高岗耀

(1.西安工业大学电子信息工程学院，陕西 西安 710021； 2.陕西华星电子集团有限公司，陕西 西安 712099)

0 引言

电磁炮作为一种以电磁发射技术为核心的先进武器系统，所适配的弹药正在从传统动能弹丸向智能弹药方向发展。在电磁炮膛内强电磁环境下的适配性问题是智能弹药能否应用于电磁炮的关键问题之一，研究强电磁环境对引信内微电子器件和集成电路的影响、干扰和损伤机理至关重要。

电子器件可靠性研究工作由理论分析和试验验证两部分组成。验证部分主要采用“加速寿命试验”，该试验分为两步：第一步是模拟特定的工作环境并将其作用于被试品的环境模拟试验；第二步是对被试品进行检验和可靠性评价的可靠性检测试验。环境模拟试验是加速寿命试验的关键之一，为后续检验分析的可靠性提供保证。针对微电子器件强电磁环境可靠性分析的研究中，文献[1]采用理论分析结合仿真进行验证，文献[2—3]通过对元器件的注入试验进行验证，文献[4]采用静电放电模拟器设计电磁环境试验进行验证。上述文献大多通过仿真或注入试验来代替加速寿命试验中的环境模拟试验，极少数采用电磁环境模拟器设计模拟试验，但也主要针对静电放电等稳态问题[5]。

强电磁环境模拟试验通过电磁发生器产生强电磁场再辅以不同的电磁场形成装置，近似模拟被试品实际工作环境。典型的电磁环境模拟器有界波电磁脉冲模拟器、偶极子模拟器、静态模拟器和混合型模拟器等。该方法具备试验条件可调节、测试简便、可重复进行、试验周期短和试验效率高等优势。因此，模拟试验在研究强电磁环境及其工程防护技术、集成电路可靠和电磁兼容相关措施的检验与评定方面发挥着重要作用。但目前为止缺乏针对电磁炮膛内强电磁冲击环境的相关模拟试验方法。因此，本文提出一种基于冲击电流发生器的电磁炮膛内强电磁环境模拟方法，为集成电路的失效机理研究提供试验支撑。

1 强电磁环境模拟试验原理

1.1 冲击电流发生器工作原理

冲击电流发生器主要由脉冲源和动作负载冲击仓组成，其中脉冲源是冲击电流发生器的核心部件。电容放电式脉冲源即为冲击电流发生器的脉冲源[6]，其原理和等效电路如图1、图2所示。

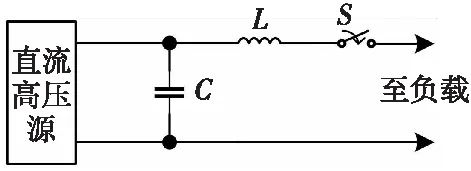
图1 电容放电式脉冲源原理Fig.1 Principle of capacitor discharge pulse source

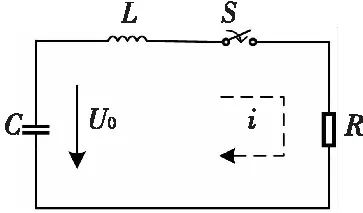
图2 电容放电式脉冲源等效电路Fig.2 Capacitor discharge pulse source equivalent circuit

电容放电式脉冲源可以看作是一个由电阻、电感、电容组成的串联放电回路。在充电回路中，直流高压源给多个或多组电容器并联充电，充电方式为整流电压或恒流方式。在放电回路中，通过间隙放电实现实负载上流过冲击电流。

冲击电流发生器的二阶微分方程为

(1)

根据电路阻尼的不同，存在三种不同的工作状态，分别为欠阻尼、临界阻尼和过阻尼状态。

设电容C上的电压降为uc(t)，初始条件和临界比[7]表达式为

i(0)=0，

(2)

(3)

uc(0)=U0，

(4)

(5)

当电路在α>1过阻尼情况下，电流表达式为式(6)，该电流是非周期性脉冲电流，电流峰值时刻表达式为式(7)，达到电流峰值的时间为式(8)。

(6)

(7)

(8)

虽然冲击电流发生器可以产生周期性和非周期性的脉冲电流，但它通常工作在过阻尼情况下，产生非周期性的脉冲电流[8]。通过对电路相关参数的调制，可以根据实际需要产生不同波形的冲击电流。

1.2 电磁环境分析

根据冲击电流发生器工作原理[9]，放电过程会在负载周围产生时变强电磁场，该环境可以近似模拟雷电放电过程中的电磁脉冲、电磁脉冲弹及电磁炮膛内强磁场等强电磁脉冲环境。

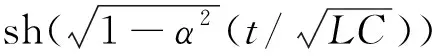
(9)

该脉冲电流激发的强电磁场是时变电磁场，在研究中直接求解时变电磁场问题往往是困难的，为简化这一过程，引入电矢势A的概念。

在时变电磁场中，麦克斯韦方程组的法拉第电磁感应定律是由两部分组成：

(10)

也就是说，在时变电磁场中存在两种不同的电场具有完全不同的性质，因而不能像静电场那样简单地引出标势，但是将B=∇×A代入式(10)，得到

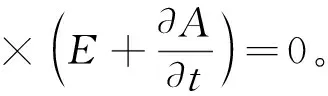
(11)

根据式(11)和场论定理二，可以引出标势φ，

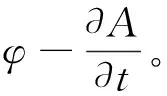
(12)

忽略全电流定律中的位移电流∂D/∂t，仅仅考虑传导电流J。J由感应电流密度Ji和冲击电流密度Jp组成。流经冲击电流发生器负载的冲击电流在负载周围产生感应电磁场，感应电流密度表达式为

Ji=σEi。

(13)

将式(11)代入式(13)，

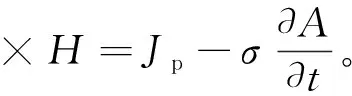
(14)

当空间中不含导磁介质时，B与H之间满足线性关系式B=μrμ0H，代入式(14)，

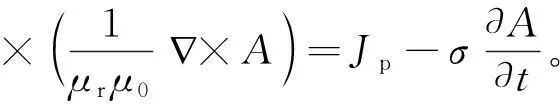
(15)

通过式(15)磁矢势A，描述负载冲击机内的磁场环境。该环境与理论分析的电磁炮膛内磁场环境具有较强的一致性[10]，理论上可以实现模拟。

2 冲击电流发生器模拟试验方法

2.1 试验参数调制

强电磁环境模拟试验的关键是最大程度地模拟实际电磁环境，这要求既要模拟电磁场的时域和频域变化，又要模拟电磁场的空间分布。通过对脉冲电流波形和负载形态的调制，可以实现对实际强电磁环境的模拟。

参数调制的第一步是选择合适的负载，负载的形状、材料和安装方式等参数直接决定冲击电流发生器内磁场的空间分布。选择负载要依据对实际电磁环境的理论分析，针对不同试验目的和重点试验区域，简化原系统的复杂结构，选择恰当器件，搭建试验环境。

确定适当负载后，对脉冲电流的波形进行调制，脉冲电流的时域和频域变化特性决定了电磁场时域和频域变化。模拟实际强电磁冲击环境的关键之一就是模拟准确的脉冲峰值和峰值时间。根据脉冲电流发生器的工作原理，脉冲电流峰值取决于电容器储能、回路电感、放电回路电阻和电容器充电电压。电容器储能和电流峰值之间成正比，理论上来说提高电容器储能可以实现提高冲击电流峰值；但是通过调整电容器储能来调制脉冲峰值的方法具有一定的局限性，当使用同一台冲击电流发生器模拟不同脉冲峰值的脉冲电流时，更换不同储能的电容器是不现实的。放电回路电阻和电流峰值之间成反比，减小负载电阻可以提高脉冲电流峰值。当脉冲电流发生器采用的脉冲峰值较高，而实际脉冲电磁场脉冲峰值较低时，调节负载电阻的方法具有一定的可行性；但是负载的形态和材料等参数会直接影响电磁场空间分布，调整电阻需要考虑多方面因素，可操作性较低。同理，回路电感对电流峰值有一定影响，但通过调节电感实现对峰值的调制不具备可行性[11]。电流峰值和充电电压之间成正比，电容器充电电压主要是由充电回路中的电源决定的，该回路和放电电路相对独立，在试验中可操作性较强。当脉冲电流发生器的负载和其他参数确定后，充电电压和电流峰值可形成固定比例关系。

峰值时间由回路电阻、电感和电容决定。当电容器放电时，负载R两端的电压为

(16)

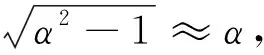
(17)

式(17)中，τ1=L/R;τ2=RC。

此时，负载r上的电压降uR(t)是双指数脉冲。根据双指数脉冲上升时间tr、衰落时间tf的定义，其与放电回路元件的参数有以下近似关系：

(18)

tf≈2.2τ2=2.2RC。

(19)

2.2 试验方案设计

冲击电流发生器和电磁炮都是通过产生脉冲电流来实现其功能，在模拟过程中可以通过参数调制得到近似的脉冲峰值和峰值时间。但是电磁炮发射过程中脉宽可以达到10 ms，冲击电流发生器产生的脉冲电流脉宽仅仅为微秒级。为解决该问题，采用多次重复试验的方法对被试品进行冲击。

基于冲击电流发生器的电磁炮膛内强电磁冲击环境模拟试验方案如下：

1) 理论分析被试引信工作区域、工作状态及强电磁环境；

2) 选择轨道炮负载或线圈炮负载，安装至负载冲击机内；

3) 确定脉冲电流i(t)、充电电压U0和冲击次数；

4) 构建电磁炮负载和被试引信三维模型，进行有限元仿真分析负载冲击机内电磁环境，判断试验可行性；

5) 按照理论分析结果，确定被试引信安装位置和角度，将被试引信固定在模拟工作区域；

6) 调制脉冲测控系统，进行强电磁环境模拟试验。

3 仿真及试验验证

3.1 冲击电流发生器内电磁环境仿真

建立冲击电流发生器负载端模型，加载强电流冲击，在有限元仿真软件COMSOL的AC/DC模块中，选择三维模型磁场接口进行瞬态仿真研究。将负载端内电磁环境与电磁炮膛内环境对比，针对提出的强电磁脉冲模拟试验方进行验证。

冲击电流发生器产生的脉冲电流为双指数脉冲电流，如图3(a)所示。根据电磁炮发射原理，仿真采用t=8 ns时电流峰值为1 MA的脉冲电流激发磁场，如图3(b)所示。

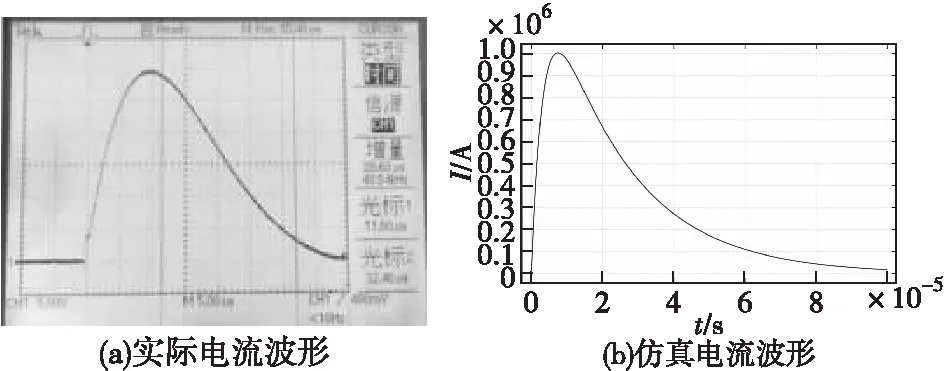
图3 脉冲电流Fig.3 Pulse current

一般轨道炮发射膛主要由两根矩形轨道、电枢和弹丸组成，电枢与轨道滑动接触，发射过程中受洛伦兹力推动弹丸加速。选择导线作为冲击电流发生器负载模拟轨道炮膛内电磁环境，建立导线模型如图4所示。

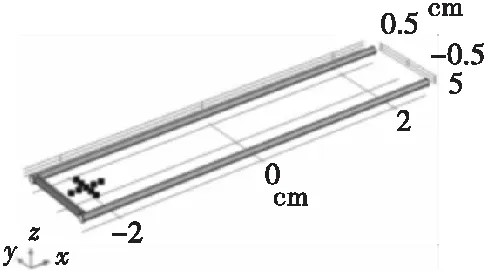
图4 轨道炮模拟模型Fig.4 Railgun simulation model

平行长导线模拟轨道，短导线模拟电枢，一般情况下，导线形态需要避免出现直角，但在本文中平行长导线与短导线连接点成直角，可以最大程度模拟电磁轨道炮电枢与轨道之间的接触。

电磁轨道炮和导线产生的强电磁场都是无限延伸的，但是考虑在实际情况下无限远处的电磁场对被试品的影响可忽略不计，故建立适当求解域，提高仿真效率。

在电磁轨道炮膛内集成电路和电子元器件等磁敏感元件通常位于电枢前端，需要重点考察电枢前端强电磁环境[12]。对应于本模型，设置如图5所示的A—I共9个观测点。观测点模拟电枢前端的集成电路，故将其设置为导电材料。在模型右端加载峰值为1 MA的脉冲电流，并设置边界条件，最后进行网格划分，如图6所示，并对建立好的模型展开瞬态研究。

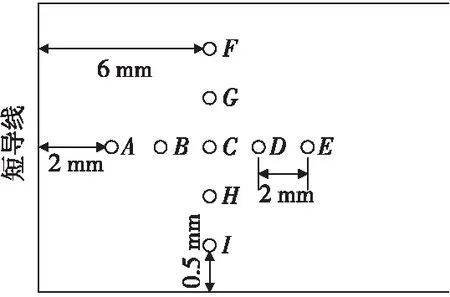
图5 观测点分布Fig.5 Distribution of observation points

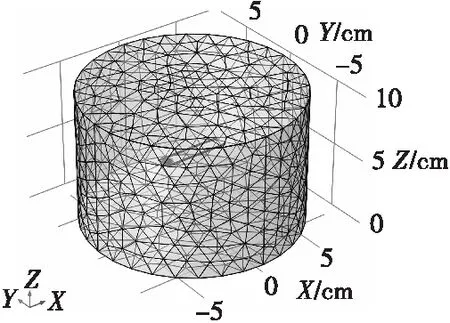
图6 网格划分Fig.6 Meshing

图7为冲击电流发生器模拟轨道炮膛内强电磁环境的磁通密度空间多切面分布。脉冲电流到达峰值时，其激发的强磁场主要集中在短导线附近，这是由短导线和平行长导线共同感应产生的。平行长导线上的磁通密度较低，且沿X轴正方向迅速减小，表现出明显的空间衰减，这一特点在图8(a)所示的模型XY方向俯视图中得到明显体现。

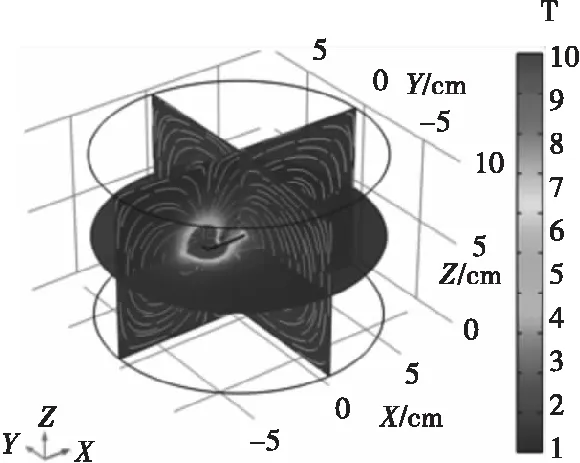
图7 磁通密度空间分布Fig.7 Spatial distribution of magnetic flux density

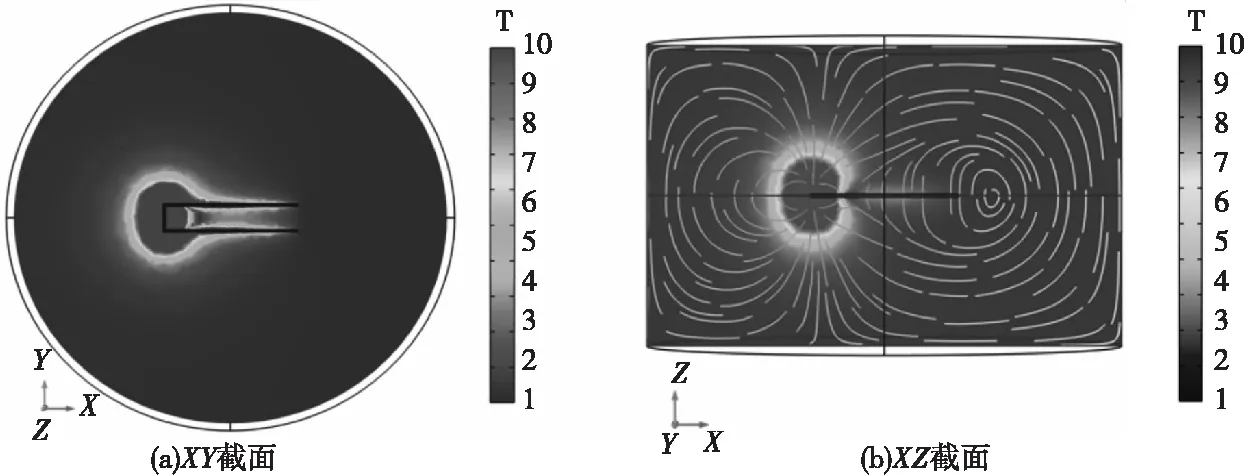
图8 切面磁通密度分布Fig.8 Sectional magnetic flux density distribution

图8(b)中，在短导线的Z轴方向磁场分布较为对称，但在X轴正方向的磁场强度比X轴负方向的弱。根据电磁炮膛内磁场理论分析及相关文献研究，电枢后端的磁场强度强于电枢前端的磁场强度，电枢上侧和下侧的磁场强度基本一致，仿真结果与实际基本一致。

模拟磁场环境在脉冲电流峰值时刻的磁场方向如图9所示。

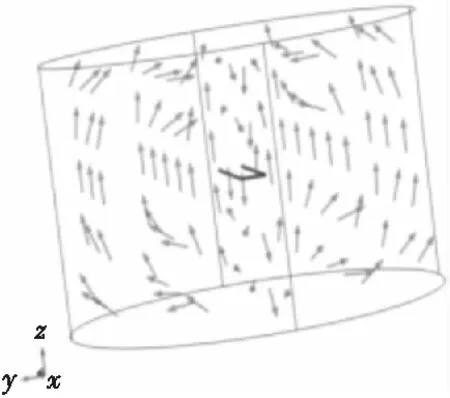
图9 磁场分布Fig.9 Magnetic field distribution

脉冲电流峰值时刻，观测点A、B、C、D、E处的磁通密度时域变化曲线如图10所示，磁通密度随参考点到短导线距离的增加逐步递减。变化趋势与脉冲电流基本保持一致，峰值时刻稍微滞后于脉冲电流峰值，这是因为当电磁场在导电介质中传播时，磁场强度相位滞后于电场强度相位，相位差与电导率和激励电流频率有关。

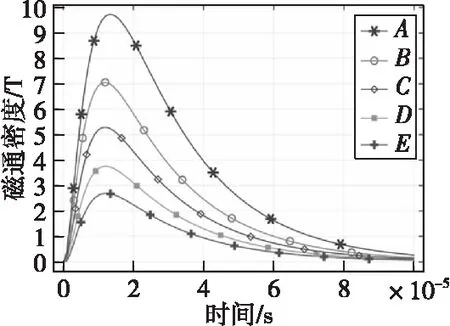
图10 A—E磁通时域变化Fig.10 Time domain change of A—E magnetic flux

由于双指数脉冲激励电流频率处于5 kHz以下属于低频，因此磁通密度峰值时刻的滞后现象并不明显。观测点F、G、C、H、I处的磁通密度分布如图11所示，靠近平行导线的参考点磁通密度显著高于其他参考点，而在平行导线内部的参考点磁通密度无明显差距。

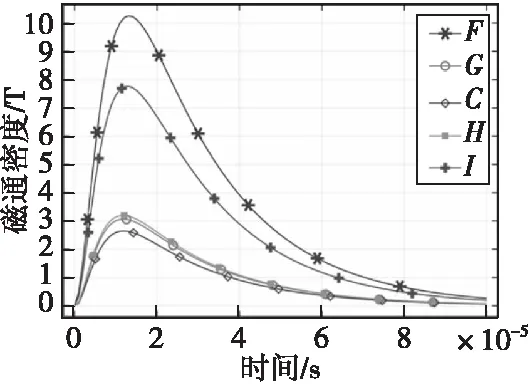
图11 F—I磁通时域变化Fig.11 Time domain change of F—I magnetic flux

对所有观测点脉冲磁场进行快速傅里叶变换得到幅频曲线图12所示，模拟磁场的频率集中在5 kHz以下的低频段。

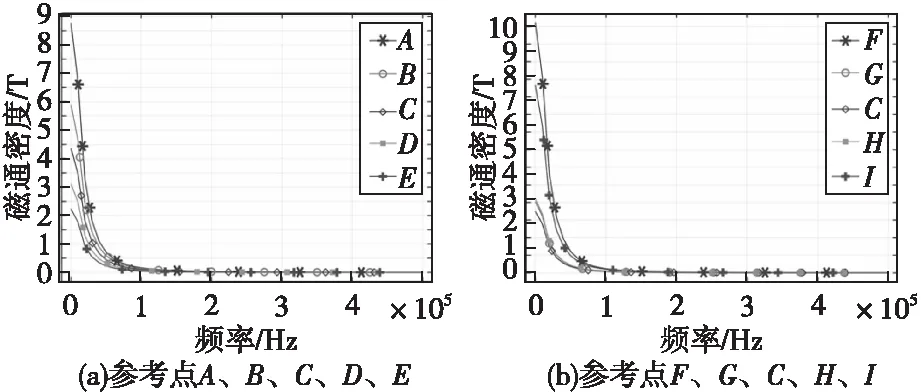
图12 观测点幅频曲线Fig.12 Observtion point mplitude-frequency curve

通过上述冲击电流发生器模拟轨道炮膛内磁场仿真分析，该磁场的空间分布、磁通密度方向和关键参考点磁通密度时域变化均符合轨道炮膛内磁场，具备进行强电磁环境模拟试验的能力。

3.2 电磁冲击环境模拟试验

在仿真分析的基础上设计对如图13(a)所示集成电路JQV300进行轨道炮膛内强电磁环境冲击模拟试验，采用冲击电流发生器型号为BS2010B组合波测系控统，如图13(b)所示。

图13 被试JQV300FPGA芯片和冲击电流发电器Fig.13 The tested JQV300FPGA chip and impulse current generator

对JQV300型FPGA进行轨道炮膛内强电磁冲击模拟试验，实际搭建试验环境如图14(a)所示。

图14 试验过程及结果Fig. 14 Experimental procedure and result

图14(b)为冲击试验结束后集成电路JQV300试验结果。对本次试验的芯片JQV300进行外观检查，试验结束时芯片表面温度对比试验前明显升高，芯片表面颜色出现明显变化。对芯片进行电学测试，结果表明芯片无法正常工作，出现失效情况，试验结果基本符合轨道炮发射过程中集成电路失效模式。

4 结论

本文提出基于冲击电流发生器的电磁炮膛内强电磁环境模拟试验方法，采用现有设备，具有搭建容易、试验安全、操作简便等特点，通过配置专用负载可方便模拟电磁轨道炮膛内强电磁环境。仿真及试验结果表明，冲击电流发生器负载端强电磁环境与电磁炮膛内理论强电磁环境的磁场强度、变化规律和空间分布具有较高一致性，满足电磁环境模拟试验要求，可以作为电磁炮膛内引信适配性研究的试验依据。