广义障碍距离变换的多因素变形研究

吴 凯 张晓莉 蔡永宁 齐 俊 王长鹏 杲广文

(济南市勘察测绘研究院, 山东 济南 250013)

0 引言

在现实世界中,两个目标物之间可以直接通行的情况较少,一般都需要绕过若干障碍物才可到达。障碍距离变换(distance transformation with obstacles,DTO)可以有效地解决此类地理空间问题,即在障碍空间中进行距离变换[1]。所谓障碍空间,指空间中具有各种障碍物(obstacles),此处的障碍物并非单指点或线或多边形,而是指全形态图形,它是点、线、面以及它们的组合,障碍本身不计算距离,并且不传递距离。空间中有生成元还有若干障碍,生成元传播的距离波需要绕过障碍进行传播。胡鹏等[2]利用地图代数的原理,解决了拥堵路段或施工路段的最短路径规划问题；刘建平[3]针对无人驾驶飞机的防撞避障和导航设计问题探讨了障碍空间的问题；秦世引等[4]基于障碍物编码的遗传算法,研究障碍空间中机器人路径规划问题；Coeurjolly等[5]针对占该空间问题,提出了离散域障碍测地线的路径算法；Willms等[6]利用网格距离传播技术,解决了障碍空间中机器人导航避障、实时路径规划的问题；Torpelund-Bruin[7]利用障碍空间V图进行了灾难应急决策研究。由上述研究可见,距离分析是障碍空间问题解算的主要途径。

本文从广义DTO概念入手,利用影响因素的逐级限制,从单点生成元到多点生层元、网络空间、街区距离等复杂要素递进式实现了若干广义障碍距离变换的派生,并通过实验进行了验证,最后总结了广义DTO及其变形在资源的合理配置、选址及路径选择等应用中具有的实际价值。

1 广义DTO

距离变换是将包含实体特征和空间背景两种像元的二值图像转变为距离图像的变换。在距离图像中,每一个像素值表示该像素到其最近的一个实体像素的距离,具体体现为每个实体的距离波不断地往外空间进行扩张,直到与邻近实体的距离波相遇。当考虑障碍空间问题时,上述距离变换则应扩展为DTO,即在障碍空间中进行距离变换。基于栅格方法的距离变换对点、直线、曲线和多边形采用通用的数据结构,即将所有的空间对象等价为标准的栅格点集,所以距离变换的生成元可以是单点也可以点、线、面的组合,甚至是不同权值的多生成元；距离变换的空间可以是匀质空间,即在所有栅格上距离的传播速度相等；也可以使非匀质空间,即在不同的区域距离的传播速度不同,以上因素可以单独或者综合影响DTO的结果,这就是广义DTO。

在实际应用中影响距离变换的因素有很多。如表1所示,从生成元类型、变换空间的性质两方面进行分类,给出了广义DTO影响因素的若干变形。

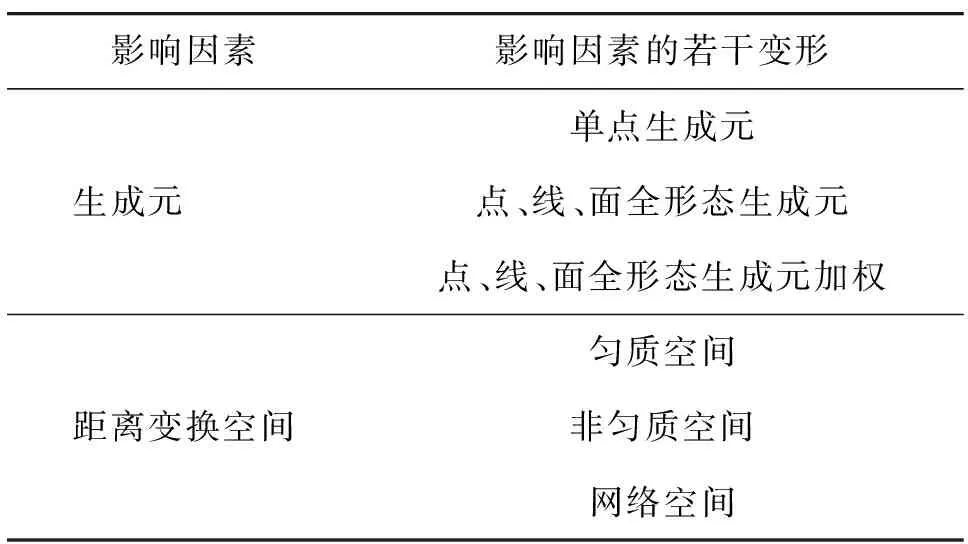
表1 广义DTO的影响因素

现实生活中,旅行所耗费的时间不仅仅与距离成正比,还与路况、运输工具性能有关,从固定点出发,旅行特定时间后所能到达的点则在各个方向上是不同距离的[8]。考虑到阻力影响,计算的距离称为耗费距离。物质在空间中移动总要花费一些代价,如资金、时间等。阻力越大耗费也越大。相应的通过耗费距离得到的距离表面称为阻力表面或耗费表面,其属性值代表耗费或阻力大小。可以根据阻力表面计算最小耗费距离[9-11],以上这些都是广义DTO在现实世界中的具体应用。

2 广义DTO的派生方法

最基本的距离变换是点状生成元在匀质无障碍空间中的距离变换,而无障碍空间只是障碍空间障碍物个数为零的一种特例。现实的地理空间不仅仅有障碍物,生成元也可以是任意形态的,各个生成元的距离传播速度可以不同,距离变换空间也可能是非匀质空间,所以将一般的DTO扩展到广义DTO具有很重要的意义[12-14]。

本节以单点无障碍匀质空间的距离变换为基础,通过变换条件的逐级限制,递进式派生出若干广义DTO。广义DTO的派生过程如图1所示,在单生成元匀质空间无障碍距离变换的基础之上加入障碍就得到了单生成元匀质空间的DTO图；按照加入非均质空间则形成单生成元非匀质空间的DTO图；若生成元的类型由单点生成元扩展为点、线、面组合的多生成元则可派生出多生成元非均质匀质空间中的DTO。

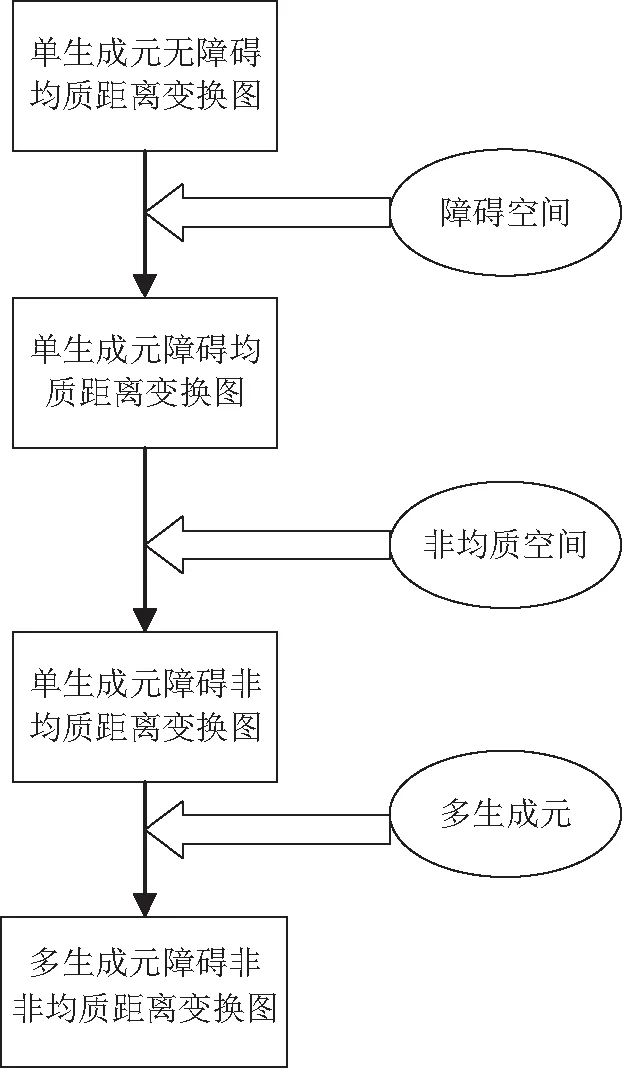
图1 广义DTO派生流程

3 实验分析

在上节中介绍了广义DTO的派生原理,即利用条件的逐级限制,递进式实现。本节就利用此方法设计广义DTO生成实验。本实验中的生成元包括点、线、面即任意形态生成元；变换空间包括障碍空间、无障碍空间、匀质空间、非匀质空间。

以生成元的性质进行分组实验,分为两组,单点生成元和点线面组合生成元。每组实验再根据变换空间的类型进行具体的划分,实验中图幅范围和比例尺全部相同。

3.1 单点生成元的广义DTO

本小节以单点无障碍匀质空间的距离变换为基础,通过添加障碍以及传播空间的均质变化,递进式派生出若干单点广义DTO,实验过程如下:

单点作为生成元的距离变换,即无障碍、匀质空间的距离变换,它的变换结果是以生成元为圆心的规则圆形,如图2所示,在图2(a)中A为点生成元。在图2(b)中,A为点生成元,B为线状障碍,C为面状障碍,距离波绕过障碍进行传播,对比图2(a)可以看出同样的图幅范围,由于障碍物的存在,距离值发生了改变,距离最大值由图2(a)中的782 m变成了2(b)中的855 m。

单点作为生成元在非匀质空间中的距离变换,在图2(c)中,A为点生成元,距离变换空间由虚线划分为1、2、3、4、5五个区域,各区域的阻力值分别为1、2、3、4、5,即距离波在区域2、3、4、5中的传播速度是区域1中传播速度的1/2、1/3、1/4、1/5倍,区域1中距离传播的速度和图2(a)、图2(b)两个图中的传播速度相等。在图2(c)中也可以看出,等距线在区域1中最为稀疏,在区域5中最为密集,说明距离波在区域1中传播最快,在区域5中传播最慢。对比图2(a)可以看出匀质空间和非匀质空间由于阻力的影响使得距离波的传播出现各向同性和各向异性的特征。

单点作为生成元在非匀质障碍空间中的距离变换,在图2(d)中,A为点生成元,B为线状障碍,C为面状障碍。变换空间和图2(c)中一样由虚线划分为1、2、3、4、5五个区域。对比图2(c)可以看出,受障碍的影响,距离值发生了改变,距离最大值由图2(c)中的2 884 m变成了图2(d)中的2 927 m。

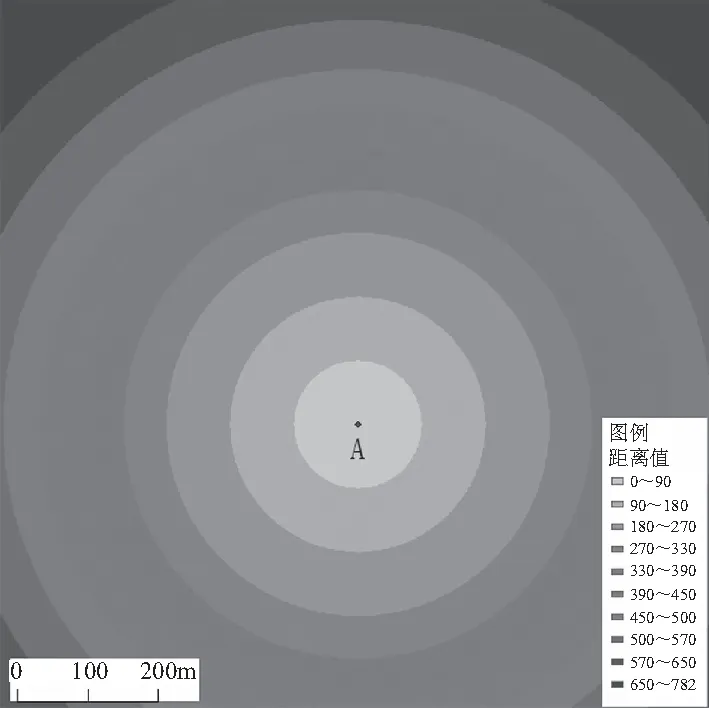
(a)匀质空间 (b)匀质障碍空间

单点生成元的广义DTO是本文研究的基础,通过设计实验,确定了障碍空间和均质空间对其距离变换的影响,为后续实验的设计、分析奠定了基础。

3.2 多生成元的广义DTO

本小节以点、线、面全形态作为生成元,进一步拓展了生成元对象,递进式派生出若干点、线、面等多生成元的广义DTO,实验过程如下:

(1)点、线、面全形态生成元距离变换。广义DTO中生成元和障碍物都应该是全形态图形,即点、线、面以及它们的组合,如图3所示。在图3(a)中,A、B、C分别为点状、面状、现状生成元。点、线、面全形态生成元DTO。在图3(b)中,A、B、C分别为点状、面状、线状生成元,a为面状障碍,b为线状障碍。距离波的传播绕开障碍物,障碍物本身不具有距离值并且不传播距离。对比图3(a)中的距离值,由于障碍物的影响,距离值有所改变,图3(a)中的距离最大值为644 m,图3(b)中的距离最大值为789 m。

(2)点、线、面全形态生成元非匀质空间距离变换。在图3(c)中,A、B、C分别为点状、面状、线状生成元。同图3(c)一样,变换空间由虚线划分为1、2、3、4、5五个区域,各区域的阻力值分别为1、2、3、4、5,等距线在区域1中最为稀疏,即距离传播速度最快；等距线在区域5中最为密集,即距离传播速度最慢。由于各区域的阻力大小不同,距离传播特定时间后在各个方向上的距离值不同,形成各向异性的距离表面。

(3)点、线、面全形态生成元非匀质空间DTO。在图3(d)中,A、B、C分别为点状、面状、线状生成元,a为面状障碍,b为线状障碍,变换空间和同图3(c)一样由曲线划分为1、2、3、4、5五个区域,对比图3(c)中的距离值可看出,由于障碍物的影响,距离波需要绕开障碍物进行传播,障碍影响区域的距离值发生变化。

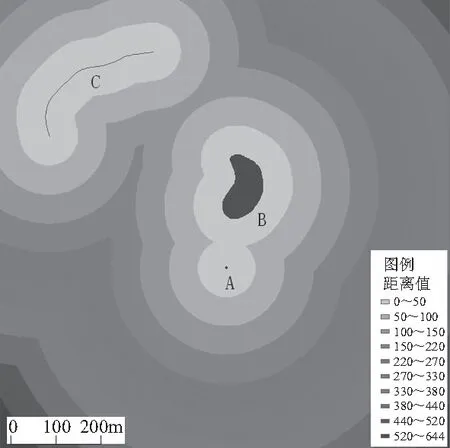
(a)匀质空间 (b)匀质障碍空间

本小节将生成元的类型由单点生成元扩展为点、线、面组合的多生成元,并按照同样的规则派生出多生成元在不同限制条件下的DTO,进一步模拟了现实空间的复杂多样性。

3.3 网络空间DTO

网络空间是指距离的传播只能在网络上进行。例如，车辆在城市道路网上行驶,若某一道路因施工等原因而禁止通行,则车辆在路网中的行驶时需绕开此段路。同样的原理,距离在网络中传播时,若在某处遇到障碍,则需寻找其他的线路进行传播[15]。网络空间中进行距离变换时,首先要将网络之外的空间设置为障碍,这样,距离的传播只能在网络中进行。网络空间中的DTO则是在网络上存在障碍物时,距离的传播需要绕过网络上的障碍物,寻找新的路径进行传播。

下面通过实验来描述网络空间DTO的原理。图4为某市的主干道路网。图4(a)为正常状态下的道路网,取路网上的两点分别设为起点(Start)和终点；以起点(Start)为生成元在道路网空间中进行距离变换,结果如图4(b)所示；随着颜色的加深距离值变大，当道路网中的某一段禁止通行时,如图4(d)所示；将此段路设为障碍,并以起点(Start)为生成元进行DTO,结果如图4(e)所示；随着颜色的加深距离值变大,利用工具成本路径(CostPath)回溯最短路径,则障碍空间中起点到终点的最短路径如图4(f)所示。

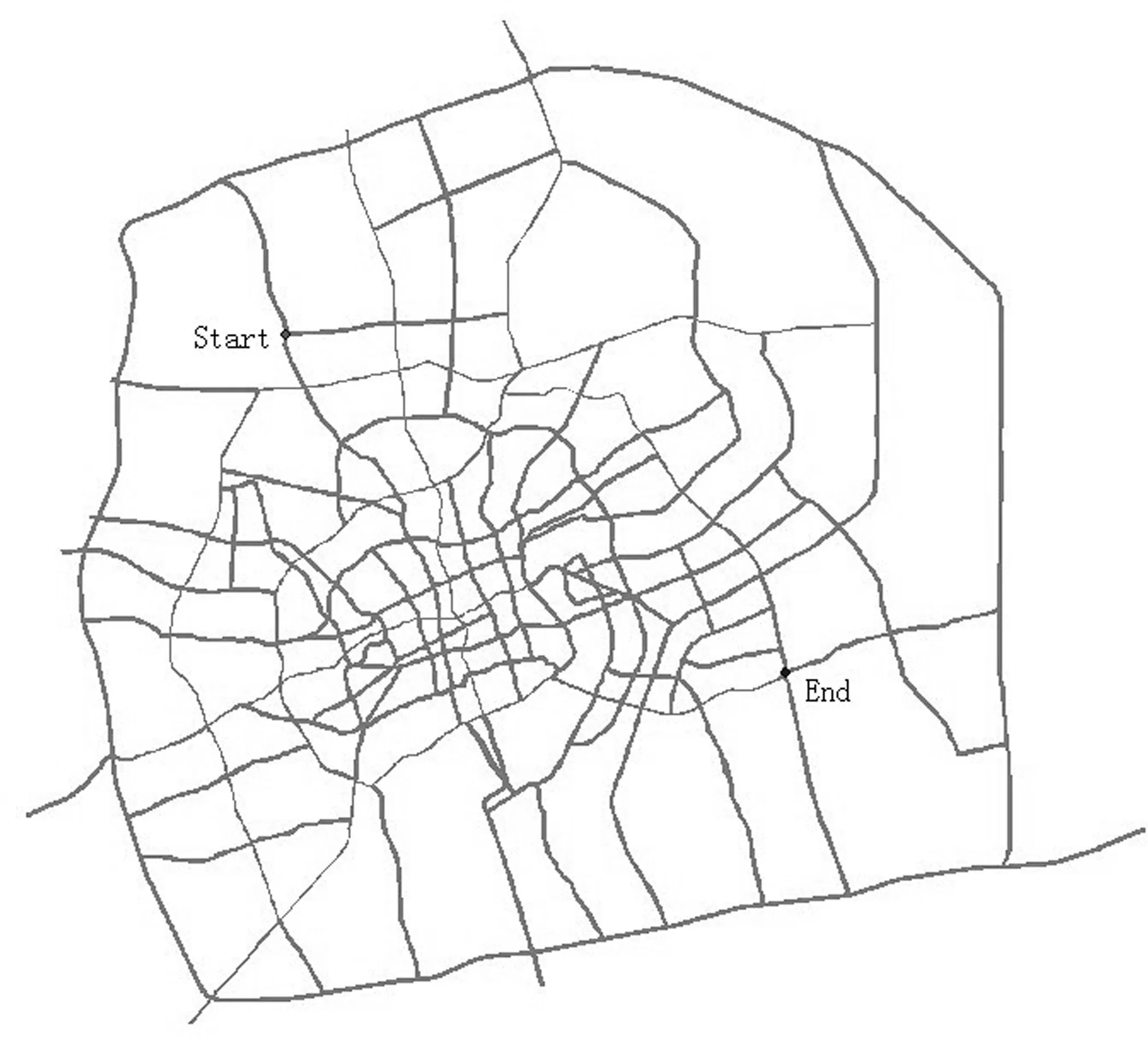
(a)无障碍道路网 (b)以起点为生成元的距离变换

网络空间中的DTO在现实生活中具有广泛的应用,像道路网避障路径、地下管网的布局等网络空间问题都可以得到很好的解决。另外,基于网络空间中的DTO而得到网络空间中的障碍V图,可以方便地划分出障碍空间中公共设施(例如,医院、医疗救助设施、公交站等)的服务范围,从而方便快捷地服务于人们的日常生活。

3.4 街区距离DTO

同网络空间类似,街区距离(即曼哈顿距离)是指平面上两点x方向距离加上y方向距离,如式(1)所示,这类距离非常适合于城市的矩形街区结构,因而称作街区距离[15]。街区距离在导航和城市路网规划中也有着非常广泛的应用。

(1)

本小节将DTO与街区距离进行融合,探讨了街区距离的DTO变换,具体的实验如下:根据街区距离的定义可得街区距离变换的原理如图5所示,在图5(a)中,生成元P其上下左右4邻域的距离值为1,对角线所对的四个像元的值由4邻域向外传播,所以值为2,以此类推。如图5(b)所示,和欧氏距离变换产生的距离波为同心圆不同,街区距离变换的距离波为同心正方形;当空间中存在障碍物,距离变换以街区距离尺度进行,则为街区距离DTO。如图5(c)所示,以中间点为生成元,四个黑色矩形为障碍,得到的街区距离DTO。从图中可以看出，距离波以同心正方形的形态向外传播。当遇到障碍时,则绕过障碍进行传播。

(a)原理图 (b)街区距离变换图

4 结束语

本文首先探讨了广义障碍距离变换概念,给出了广义DTO的派生方法及具体流程,并以单点生成元、多生成元、网络空间、街区距离等广义DTO影响因素及变形为分析对象进行了实验验证,获得了广义DTO影响因素及变形的适用性。实验结果表明:单点生成元的广义DTO是基础,确定了障碍空间和均质空间对变形的影响；多生成元的广义DOT实验则在将生成元进行拓展模拟了现时空间的多样性；网络空间DTO实验和街区距离DTO实验则表明了广义DTO变形的适用性在资源的合理配置、选址及路径选择等应用中具有一定实际价值。