余强制映射的广义半闭性原理及应用

曾炫淇， 罗馨缘， 冯世强

(西华师范大学 数学与信息学院， 四川 南充 637009)

0 引言

半闭性原理在不动点算法的收敛分析中起着重要的作用.半闭性的概念阐明了映射的拓扑性质，特别是在考虑弱拓扑的情况下.更确切地说，给定一个Hilbert空间H中的弱序列闭子集D,我们说映射T:D→H在x∈D是半闭的，如果对于D中每个序列{xk}都弱收敛到x,T(xk)强收敛到u,有T(x)=u.

根据其定义，当T是弱序列连续时，半闭性平凡成立；然而它在一般情况下并不成立，相关理论及证明可见文献[1].设Id表示H上的单位映射.非扩张映射理论中的一个基本结果是著名的Browder半闭性原理[2]，即如果T是非扩张的，那么映射Id-T在D中每一点都是半闭的.Browder的结果适用于更一般的情况，到目前为止，已经成为研究非扩张映射的渐近性质和遍历特性的关键工具[3-9].

Bauschke[10]将Browder半闭性原理推广到了有限多个稳定非扩张映射的情况.Bartz等[11]根据Bauschke的结果，将稳定非扩张映射做到了范围更广的余强制映射和锥平均映射.

本文主要是将文献[11]中关于余强制映射的半闭性原理由原来n个相同的Hilbert空间构成的H×H×…×H在一定条件下推广到n个不同的Hilbert空间构成的H1×H2×…×Hn上，并且改进了收敛条件，使其算子适用范围更广，进一步也得到了文献[10]中关于稳定非扩张映射的广义原理，还考虑了收敛条件中不带余强制系数的情况.

1 基本概念和预备知识

本文在n个空间交集非空的情况下，将余强制映射的半闭性原理推广到更广的空间并修改了收敛条件使之范围更广.为此，我们在加权内积空间中应用并推广了文献[11]中的技术和结果.

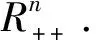
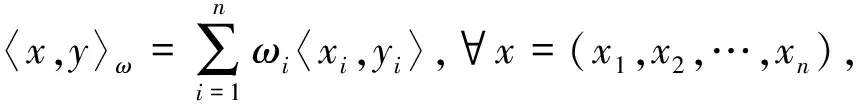
y=(y1,y2,…,yn)∈H,xi,yi∈Hi.

(1)

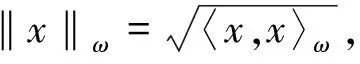
若γ=(γ1,γ2,…,γn)∈n{(0,0,…,0)},则H的子空间C定义为C={(γ1x*,γ2x*,…,γnx*)：x*∈H*}.下面我们给出了PC的投影形式.

引理1若x=(x1,x2,…,xn)∈H,则x在C上的投影为PC(x)=(γ1u*,γ2u*,…,γnu*),其中

(2)

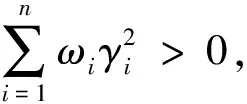
〈z,x-y〉ω=

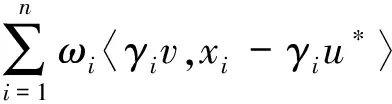
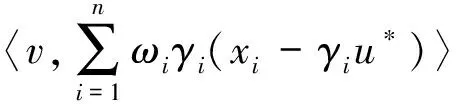
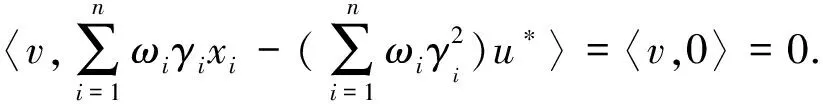
定义1[11]设D是H中的一个非空子集，T：D→H是一个映射，设γ>0,θ>0,我们说

(i)映射T是非扩张的，如果

‖T(x)-T(y)‖≤‖x-y‖,∀x,y∈D；

(ii)映射T是稳定非扩张的，如果

‖T(x)-T(y)‖2+

‖(Id-T)(x)-(Id-T)(y)‖2≤

‖x-y‖2,∀x,y∈D,

等价于

〈x-y,T(x)-T(y)〉≥

‖T(x)-T(y)‖2,∀x,y∈D；

(iii)映射T是γ-余强制的，如果γT是稳定非扩张的，即

〈x-y,T(x)-T(y)〉≥

γ‖T(x)-T(y)‖2,∀x,y∈D.

引理2设D是H中的一个非空子集，T：D→H是一个映射，设γ>0,θ>0.如果T是γ-余强制的，那么它对于任意的γ′∈[0,γ]都是γ′-余强制的.

证明根据定义1(iii)显然得到.

引理3映射T是稳定非扩张的当且仅当T是1-余强制的；当γ≥1时，一个γ-余强制的映射是稳定非扩张的.

证明通过定义1(ii)(iii),我们得到映射T是稳定非扩张的当且仅当T是1-余强制的，再应用引理2可知当γ≥1时，一个γ-余强制的映射是稳定非扩张的.

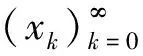
xk⇀x,

(3a)

T(xk)⇀y,

(3b)

T(xk)-PC(T(xk))→0,

(3c)

(xk-T(xk))-PD(xk-T(xk))→0,

(3d)

则y∈C,x∈y+D,并且y=T(x).

引理5设x,y∈H,C是H的子空间，则有Px+C⊥(y)=x+PC⊥(y-x).

证明由文献[1]的Proposition 3.19及C⊥为闭凸集可知结论成立.

2 主要结果

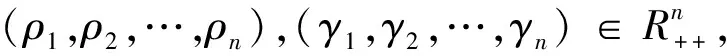
∀i∈{1,2,…,n},xi,k⇀xi,

(4a)

∀i∈{1,2,…,n},Ti(xi,k)⇀yi,

(4b)

(4c)

∀i,j∈{1,2,…,n},Ti(xi,k)-Tj(xj,k)→0,

(4d)

则对∀i∈{1,2,…,n},都有Ti(xi)=yi.

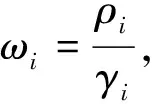
T(z)=(γ1T1(z1),γ2T2(z2),…,γnTn(zn)),

z=(z1,z2,…,zn)∈H.

然后对于每个u=(u1,u2,…,un),v=(v1,v2,…,vn)∈H,由于Ti是γi-余强制的，我们有

〈u-v,T(u)-T(v)〉ω=

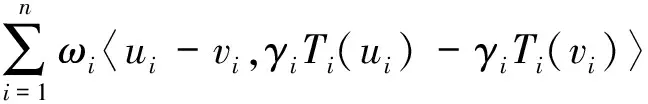
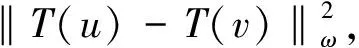
所以T是稳定非扩张的.设x=(x1,x2,…,xn),y=(γ1y1,γ2y2,…,γnyn),对于每个k=0,1,2,…,设xk=(x1,k,x2,k,…,xn,k),则有

xk⇀x,T(xk)⇀y.

(5)

H中的仿射子空间C和D定义为C={(γ1x*,γ2x*,…,γnx*)：x*∈H*},D=x-y+C⊥.所以C-C=(D-D)⊥.因此根据引理1，我们可以得到

其中

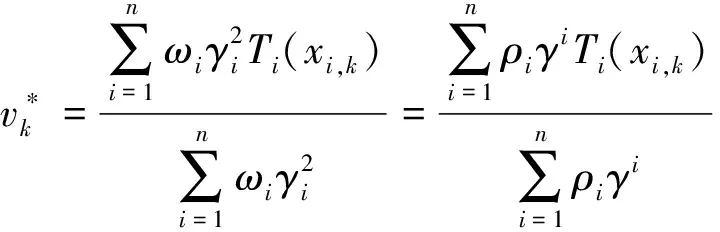
(k→∞),所以我们可以得到

T(xk)-PC(T(xk))→0.

(6)

应用引理1定义的投影

其中

其中

PC(xk-T(xk))→PC(x-y).

所以，

xk-T(xk)-PD(xk-T(xk))=

xk-T(xk)-Px-y+C⊥(xk-T(xk))=

(7)

xk-T(xk)-(x-y+PC⊥(xk-T(xk)-

(x-y)))(见引理5)=

(Id-PC⊥)(xk-T(xk))-(Id-PC⊥)(x-y)=

PC(xk-T(xk))-PC(x-y)→0,

最后，由(5)-(7)及引理4得到y=T(x),也就是对于∀i∈{1,2,…,n},有Fi(xi)=yi.

注1当H1=H2=…=Hn时，由(4b)(4d)可知y1=y2=…=yn,定理1就退化到了文献[11]中的定理3.1.

应用定理1，我们进而得到稳定非扩张映射的广义半闭性原理.

∀i∈{1,2,…,n},xi,k⇀xi,

(8a)

∀i∈{1,2,…,n},Ti(xi,k)⇀yi,

(8b)

(8c)

∀i,j∈{1,2,…,n},Ti(xi,k)-Tj(xj,k)→0,

(8d)

则对∀i∈{1,2,…,n},都有Ti(xi)=yi.

证明根据前面引理3可知映射T是稳定非扩张的当且仅当T是1-余强制的，所以只需令定理1中γ1=γ2=…=γn=1,ρ1=ρ2=…=ρn=1即可证得.

注2我们发现当H1=H2=…=Hn时，由(8b)(8d)可知y1=y2=…=yn,定理2就退化到了文献[10]中的定理3.1.

注3定理2中，令n=1时，我们就得到了引理4的一个特殊情况：C=H和D={x-y},其等价于文献[2]中Browder最初的半闭性原理(或文献[1]中的定理4.27).

注4我们发现在定理2中应用稳定非扩张映射γ1T1,γ2T2,…,γnTn,可以直接推出余强制映射的广义半闭性原理.但是这并不能产生定理1：这种情况下，余强制系数会出现在(8b)和(8d)中，然而它并不包含在(4b)和(4d)中.

我们发现在定理1的条件(4)中，除了(4c)以外，其余都是没有余强制系数γi的.所以我们考虑当不同算子收敛到同一点(设y1=y2=…=yn=y*)的特殊情况，从而我们不在任何收敛条件中加入余强制系数γi,但作为交换，我们对这些余强制系数γi也施加了一定的平衡条件.

定理3(平衡余强制映射的广义半闭性原理)对于每个i∈(1,2,…,n),Ti:Hi→H*都是γi-余强制映射

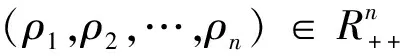
(9)

进一步假设

∀i∈{1,2,…,n},xi,k⇀xi,

(10a)

∀i∈{1,2,…,n},Ti(xi,k)⇀y*,

(10b)

(10c)

∀i,j∈{1,2,…,n},Ti(xi,k)-Tj(xj,k)→0,

(10d)

则对∀i∈{1,2,…,n},都有Ti(xi)=y*.

证明基于式(9)，我们可取

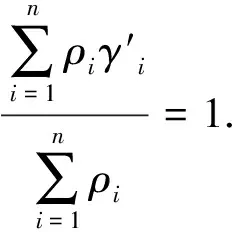
ρ1(γ1-1)+ρ2(γ2-1)+…+ρn(γn-1)=0.

(11)

条件(10a)(10b)和(10d)分别和前面的(4a)(4b)和(4d)是一致的.因此我们利用定理1还需证(4c)成立.实际上，结合(10c)(10d)和(11)，我们可得

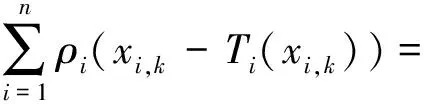
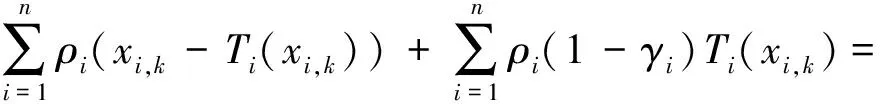
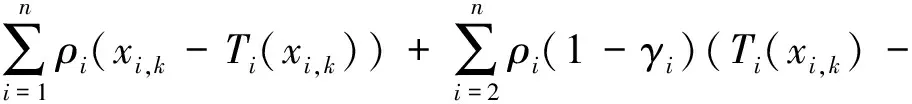
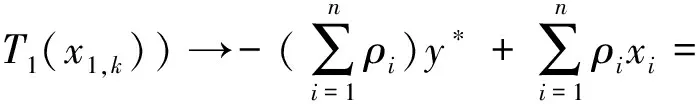
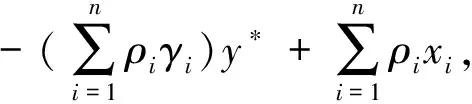
这实际也就是当y1=y2=…=yn=y*的(4c).最后，通过应用定理1可得：∀i∈{1,2,…,n},有Ti(xi)=y*.

注5通过定理2和定理3，我们注意到关于余强制映射的条件(10)实际上是关于稳定非扩张映射的条件(8)的加权版本.但余强制映射需要满足均衡条件(9)，即余强制系数的加权平均至少为1，这对稳定非扩张映射才总是正确的(见引理3).

3 今后工作

在本文中，我们将余强制映射的半闭性原理推广到了n个有非空交集的Hilbert空间构成的空间，并改进了收敛条件使其适用范围更广.在今后，我们将进一步在任意n个Hilbert空间构成的空间中来研究半闭性原理，以及更弱的收敛条件.