不同先验下反向帕累托分布形状参数的估计
蓝 海, 徐 宝
(吉林师范大学 数学学院, 吉林 四平 136000)
0 引言
反向帕累托分布的密度函数和分布函数分别为
f(x;θ,α)=αθ-αxα-1,0
F(x;θ,α)=θ-αxα,0
其中α为形状参数,θ为位置参数,简记为RP(θ,α).目前关于反向帕累托分布的理论研究相对较少,实际应用偏多,如:文献[1]在研究帕累托种群时使用了反向帕累托分布;文献[2]首次提出将反向帕累托分布应用于城市人口分布的研究中;文献[3]使用RP(θ,α)分布拟合我国居民收入;文献[4]将RP(θ,α)分布与其它分布进行组合得到了形式更为灵活的组合分布模型.理论研究的仅有文献[5]反向帕累托分布参数估计及应用.
但文献[5]并没有讨论RP(θ,α)分布形状参数的E-Bayes估计,E-Bayes估计最早由文献[6]提出,目前该方法已经具有充分的发展,如:文献[7]使用E-Bayes估计研究超参数选择对先验的影响;文献[8]给出了逆威布尔分布参数E-Bayes估计的新公式;文献[9]认为Ⅱ型截尾数据下双参数浴缸型寿命分布参数的E-Bayes估计优于Bayes估计;文献[10]发现参数的E-Bayes估计更便于计算与应用;文献[11]运用E-Bayes估计得到了失效概率pi的点估计.因此本文将在不同先验信息下,使用加权p,q对称熵损失函数
(1)
在位置参数θ给定时,研究反向帕累托分布形状参数α的Bayes估计以及E-Bayes估计,并通过使用MCMC算法进行仿真模拟比较估计之间的性能,进而巩固反向帕累托分布的理论研究.
1 形状参数的Bayes估计
使用Bayes分析往往需要利用先验信息,当先验信息只有极少甚至没有先验信息时可以使用共轭先验以及Jeffreys无信息先验,因此本节分别在共轭先验与Jeffreys无信息先验下,使用损失函数(1)得出当位置参数θ已知时,RP(θ,α)分布形状参数α的Bayes估计的表达式.
定理1.1设X1,X2,…,Xn为来自RP(θ,α)分布的一组样本,记X=(X1,X2,…,Xn),在损失函数(1)下,对于任意的先验分布,形状参数α的Bayes估计为
证明任意选取一个参数α的估计量δ(X),在损失函数(1)下,δ(X)的Bayes风险为
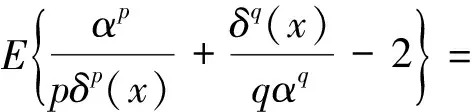
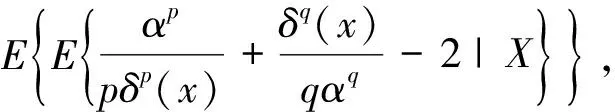
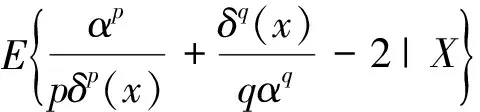
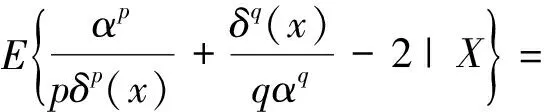
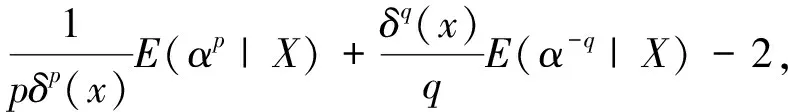
推论1.1若RP(θ,α)分布的形状参数α的先验分布为Γ(β,γ),其中参数β、γ均为定值,则在损失函数(1)下,形状参数α的Bayes估计为
δB(X)=
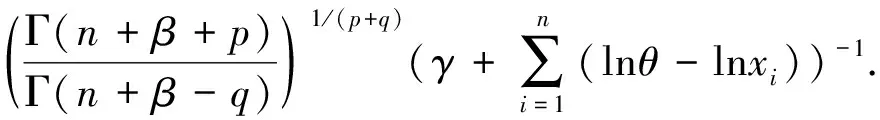
证明由于形状参数α的先验分布为Γ(β,γ),于是有
又因为RP(θ,α)分布的密度函数为f(x;θ,α)=αθ-αxα-1;0
因此形状参数α的后验密度为
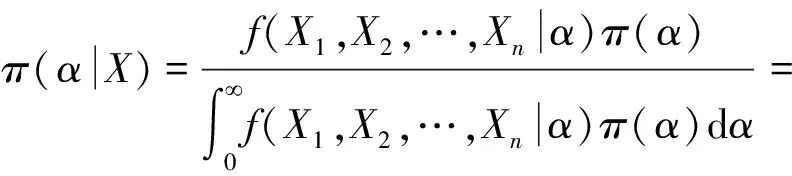
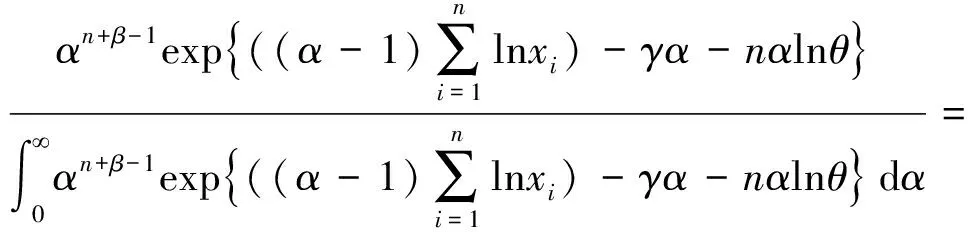
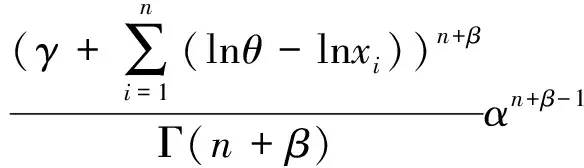
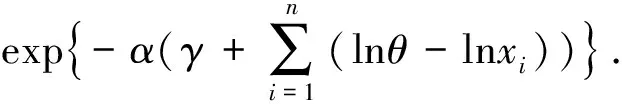
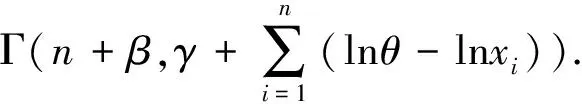

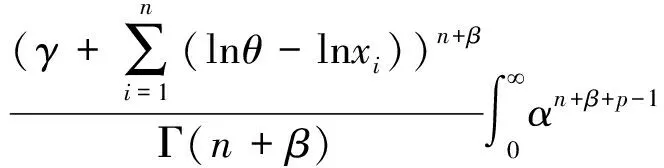
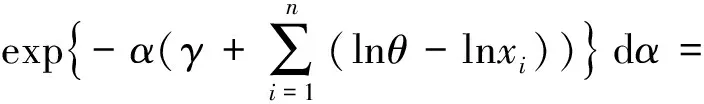
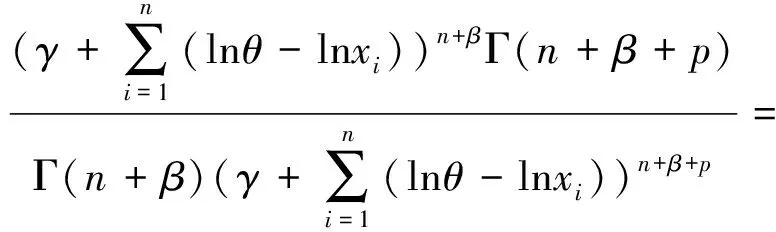
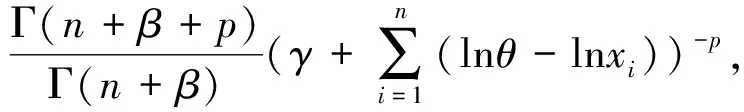
同理可得
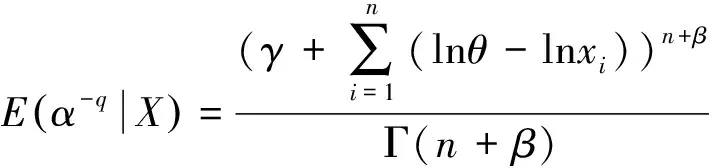
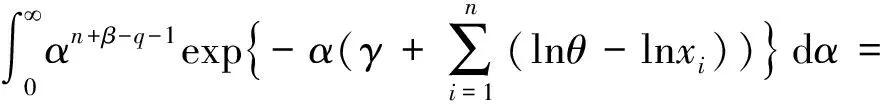
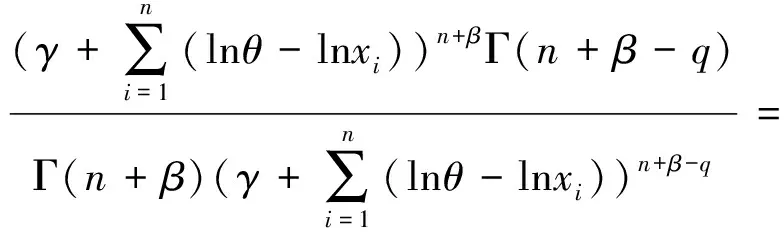
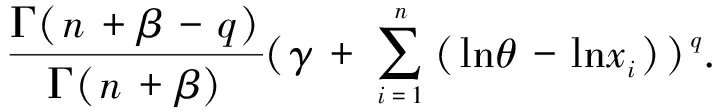
由定理1.1易知,α的Bayes估计为
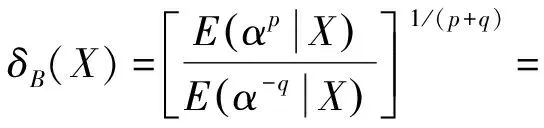
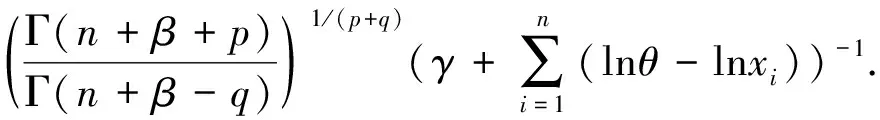
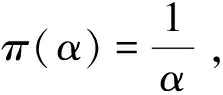
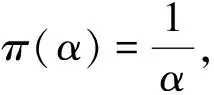
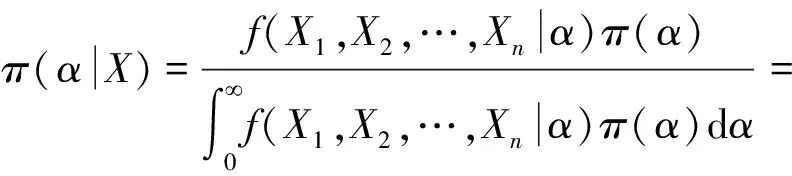
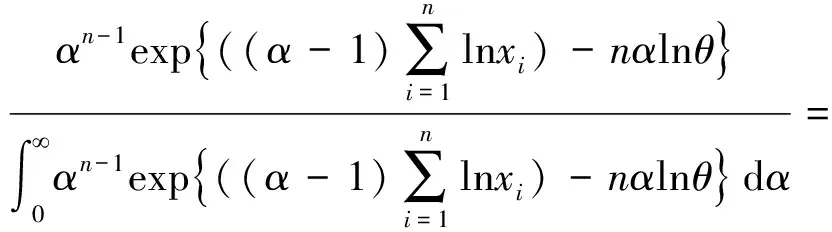
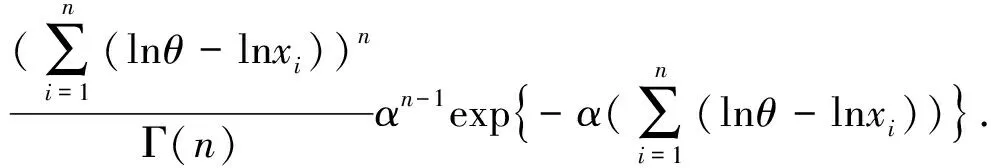
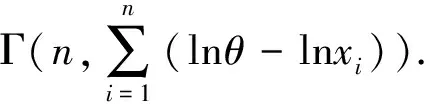

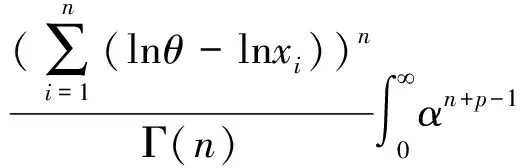
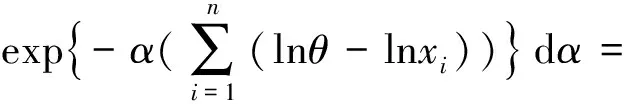
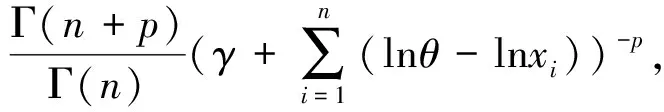
同理可得
E(α-q|X)=
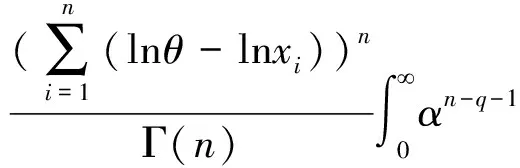
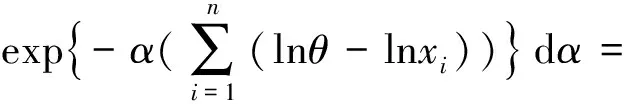
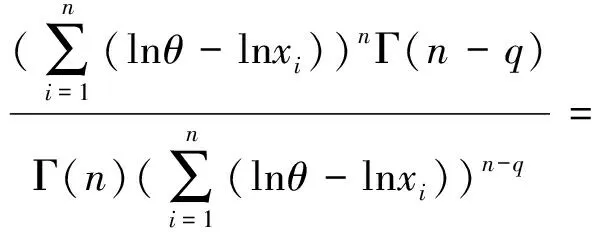
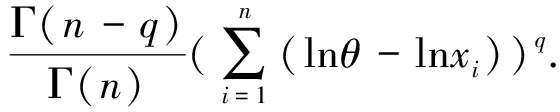
由定理1.1易知,α的Bayes估计为
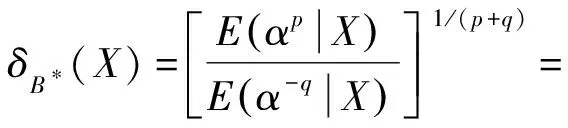
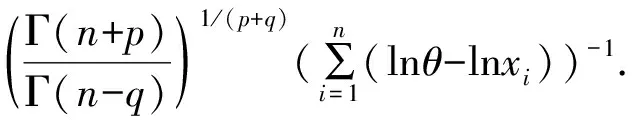
2 形状参数的E-Bayes估计
使用共轭先验推导Bayes估计时,出现了两个新的参数β、γ,为了简化计算在上一节中人为地将这两个参数设为已知量,这种方法可能会影响估计的仿真性,因此本节结合文献[12]给出了形状参数α的E-Bayes估计进而降低新参数对估计仿真性的影响.
定理2.1RP(θ,α)分布中的形状参数α在损失函数(1)下的E-Bayes估计为
δEB(X)=
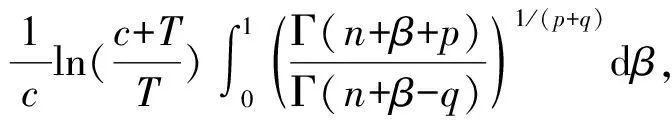
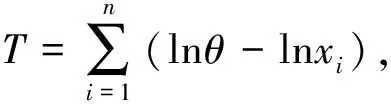
证明由推论1.1可知参数α在损失函数(1)下的Bayes估计为
δB(X)=
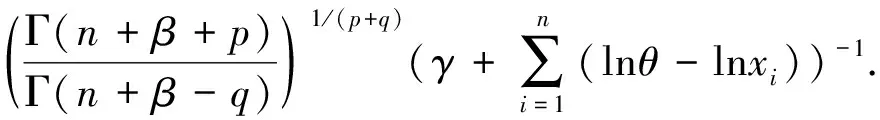
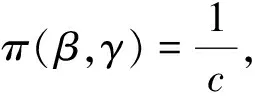
δEB(X)=

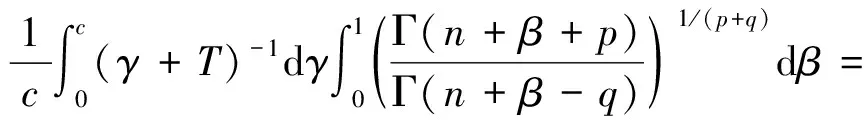
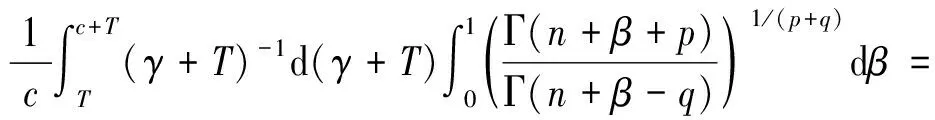
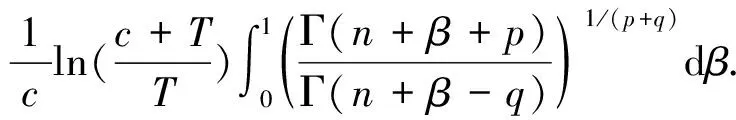
3 随机模拟
由于所得的估计中含有常数p,q,c,为了更好地比较估计之间的性能,首先通过取Be(1,1)为提议分布,分别在θ=1以及α=(0.05,0.2,1.5,4)下运用R软件进行MCMC模拟,通过1000次的迭代其中Markov链如图1所示.
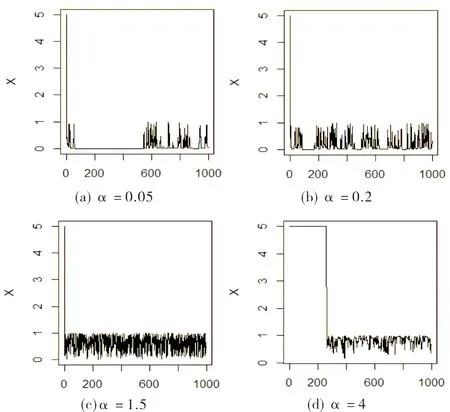
图1 θ=1时α=(0.05,0.2,1.5,4)的迭代图
由图1可以发现,当α=1.5时迭代效果较好.接下来为了使结果更具有一般性,在α=1.5的条件下选取θ=(5,10,100,1000)进行MCMC模拟,结果如图2所示.
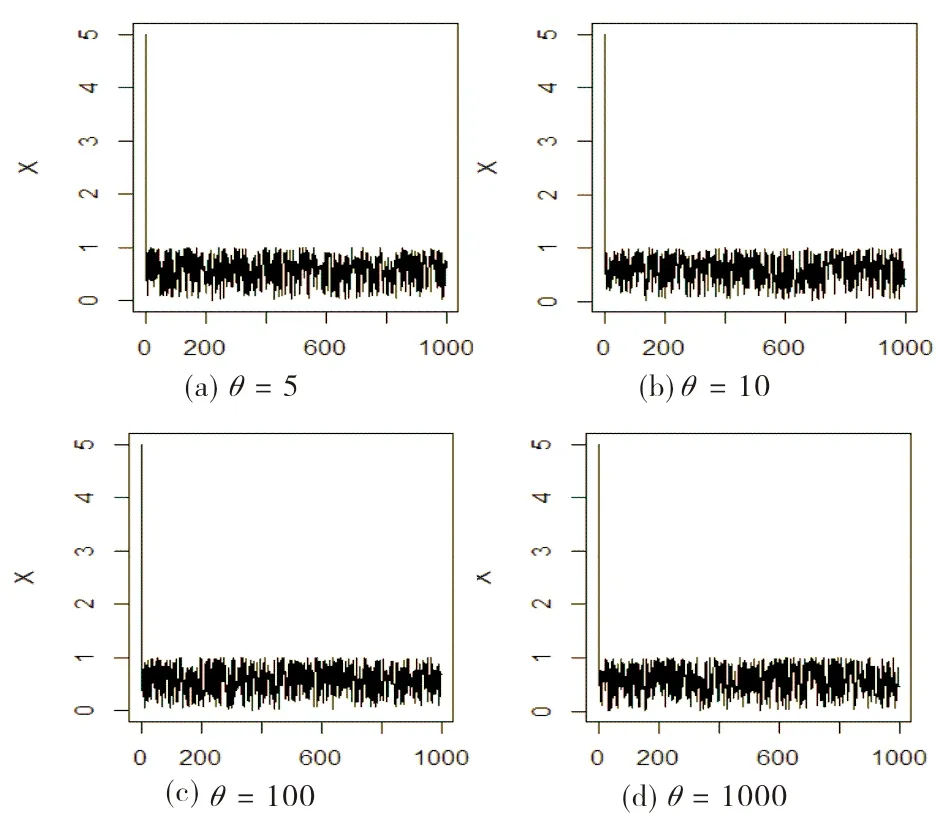
图2 α=1.5时θ=(5,10,100,1000)的迭代图
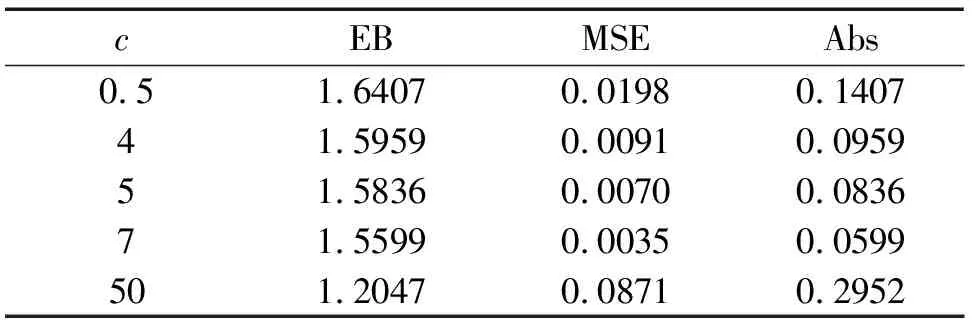
由图2可以发现,参数θ对模拟结果影响较小,因此为了便于后续计算,选取θ=1并从该链生成的数据中截取第501到第600之间的数据作为容量n=100的样本,其次分别在p≠q与p=q以及β=0.5,γ=1条件下根据所得样本进行数值模拟,模拟结果如表1至表3所示,表中结果均为模拟结果的平均值,其中Bayes表示形状参数α的贝叶斯估计,MSE表示估计的均方误差,Abs表示偏差的绝对值.
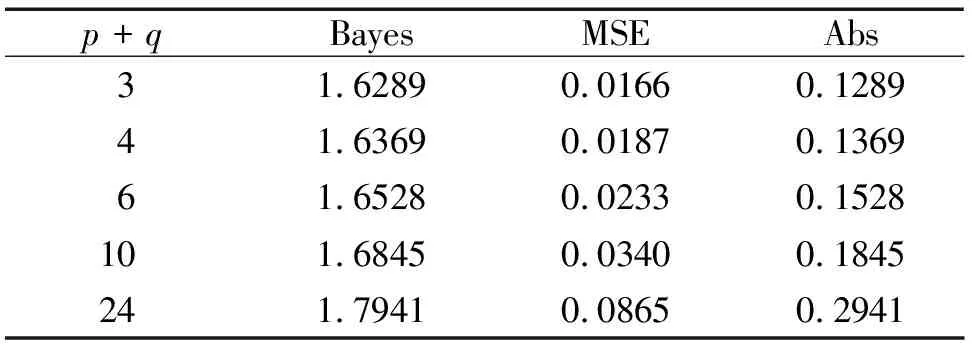
表1 共轭先验下形状参数Bayes估计的模拟结果(θ=1,α=1.5,q=1,p>q)
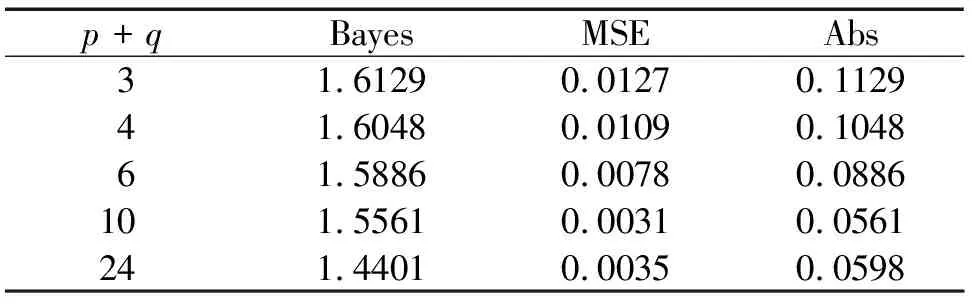
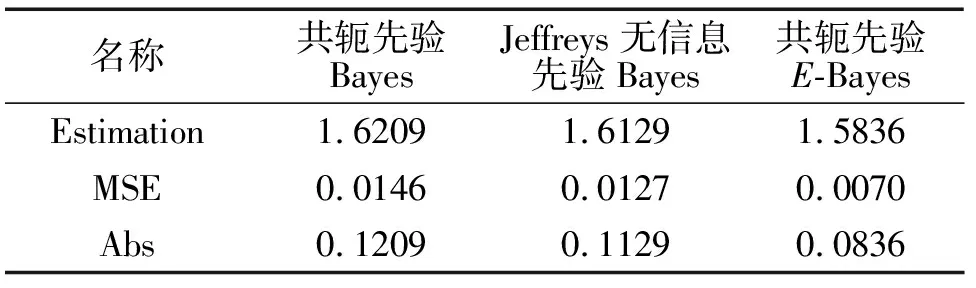
表2 共轭先验下形状参数Bayes估计的模拟结果(θ=1,α=1.5,p=1,p 表3 共轭先验下形状参数Bayes估计的模拟结果(θ=1,α=1.5,p=q) 由表1至表3可以得出: (1)当参数p大于q时,随着p,q之间的值相差越来越大,形状参数α的Bayes估计和均方误差以及偏差的绝对值都有递增的趋势.当p小于q时,随着p,q之间的值相差越来越大,形状参数α的Bayes估计和均方误差以及偏差的绝对值都有递减的趋势,但是当p,q之间的值差达到某一峰值时,Bayes估计、MSE、Abs开始递增. (2)当参数p,q相等时,随着p,q的改变,形状参数α的Bayes估计的均分误差和偏差的绝对值波动较小相对稳定,因此在使用加权p,q对称熵损失函数对反向帕累托分布形状参数α进行更深入的研究与探讨时,若要求精度较高,对于参数p,q的选取应适当将q的值稍大于p的值,但是若不要求精度,可以将参数p,q取为相等的数,可以使得到的结果相对稳定. 最后根据上述结论,为了得到波动较少的稳定值,接下来在p=q=1以及c=(0.5,4,5,7,50)的条件下对E-Bayes估计进行仿真模拟.模拟结果如表4所示,其中EB表示形状参数α的E-Bayes估计 表4 形状参数E-Bayes估计的模拟结果(n=100,α=1.5,p=q=1,θ=1) 由表4可以发现c=(4,5,7)的稳健性较好,因此居中选取c=5时的结果与不同先验下Bayes估计的仿真结果进行比较,比较结果如表5所示. 表5 形状参数估计的模拟结果(n=100,α=1.5,p=q=1,θ=1,c=5) 由表5可以得出下述结论: (1)E-Bayes估计和MSE以及Abs的值相比Bayes估计具有较好的仿真性,因此可以得出E-Bayes估计能够有效地降低先验信息中所含新参数对结果的影响. (2)在共轭先验与Jeffreys无信息先验下的估计都与真值相差较小,从而进一步验证了无信息先验对Bayes分析的影响较小是可以接受的. 针对反向帕累托分布的参数估计体系还不够丰富,以及E-Bayes估计的广泛使用,本文通过Bayes分析,探讨了反向帕累托分布的形状参数α在不同先验信息下,使用加权p,q对称熵损失函数分别得到了相应的Bayes估计,通过并结合相关定义以及文献,给出了反向帕累托分布的形状参数α的E-Bayes估计.最后运用R软件使用MCMC算法进行仿真模拟,通过模拟结果验证了无信息先验是可以接受的以及E-Bayes估计的仿真性优于Bayes估计,从而完善了反向帕累托分布的参数估计体系.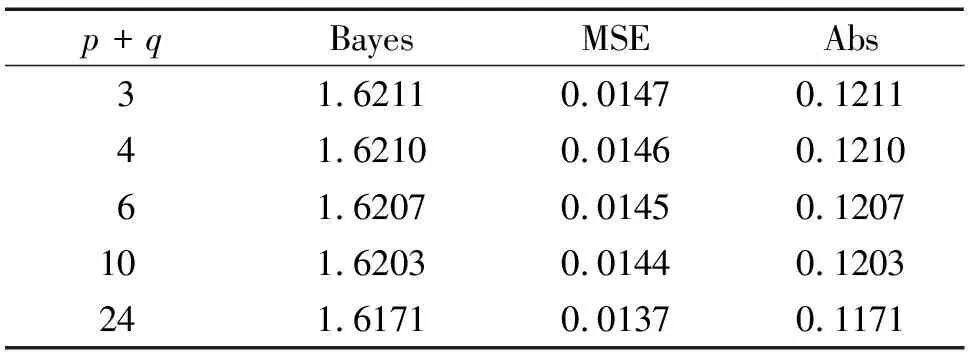
4 结束语

