基于CFD-DEM的离心泵叶轮磨损特性研究和优化设计

刘 栋，倪子建，黄 凯，王卫华，严建华

（1.江苏大学 能源与动力工程学院，江苏镇江 212013；2.江苏双达泵业股份有限公司，江苏泰州 214537）

0 引言

离心泵在矿业、农业、化工等行业中用于固液两相流的输送［1-5］，固体颗粒对离心泵的磨损直接影响泵的水力性能和使用寿命［6-7］，对磨损部件频繁的维护和更换使得离心泵的使用成本显著增加［8-9］。因此，针对离心泵磨损特性的研究和优化设计亟待开展。

叶轮是最容易受到颗粒磨损的过流部件［10］，WANG等［11］采用DDPM模型研究了颗粒的粒径和浓度对叶轮的磨损特性影响，发现随着粒径的增大，压力面中间、吸力面前端的磨损更严重，而随着颗粒浓度的增加，叶片压力面磨损的面积扩展，磨损量增加；TANG等［12］采用CFD-DEM模型研究了不同球形度颗粒对离心泵叶轮的磨损特性影响，发现随着球形度的增大，压力面颗粒的浓度增加；黄思等［13］采用CFD-DEM模型分析了不同流量下离心泵叶轮的磨损特性，发现随着流量增大，叶轮叶片工作面和后盖板磨损增加显著。上述文献针对粒径、浓度、球形度、流量等参数对叶轮磨损特性的影响做了大量研究工作，但关于叶片几何参数对叶轮磨损特性影响的研究较少。

随着计算机技术和CFD理论的发展，离心泵的参数化全局优化设计方法也不断丰富。基于试验设计和数值模拟得到大量样本数据，采用正交试验法、响应面法、人工神经网络法、径向基函数法等优化方法，能够回归拟合优化参数与目标之间的近似函数关系，通过遗传算法等各类优化算法进行寻优求解［14］，获得最优参数方案。其中响应面法通过多项式模型拟合复杂的函数关系，能够高效求解各因素水平响应值。张德胜等［15］采用响应面法，以氟塑料两相流泵的效率和磨损率为优化目标，分析了泵结构参数之间存在的交互影响；杨煜兵等［16］采用响应面法，选取柱塞泵迷宫密封槽几何参数为优化变量，以泄漏量最小为优化目标进行优化设计，获得了泄漏量降低97.3%的改进模型。

本文选取叶片出口安放角、进口安放角和包角作为研究参数，采用CFD-DEM耦合方法计算离心泵叶轮磨损，分析叶轮几何参数对过流部件磨损特性的影响规律。采取响应面优化方法，以平均磨损率和效率为优化目标，对离心泵进行优化设计。

1 计算模型及方法

1.1 CFD-DEM离散元方法

本文基于拉格朗日方法追踪模型泵内的颗粒运动，通过求解牛顿运动方程确定颗粒的位置与速度。颗粒的运动方程如下：

式中 mi，vi——颗粒i的质量的速度；

Fnij——颗粒i和颗粒j之间的法向接触力；

Ftij——颗粒i和颗粒j之间的切向接触力；

Ffpi——液相对颗粒i的作用力（如压力梯度力、阻力等）；

Fgi——颗粒i的重力；

Ii——颗粒i的转动惯量；

ωi——颗粒i的旋转速度；

Tij——颗粒 i，j之间的滚动摩擦力矩。

基于欧拉方法计算液相的运动，液相的连续性方程为：

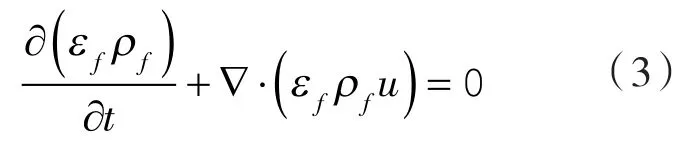
式中 εf——液相的体积分数；

ρf——液体的密度；

t——时间；

u——液体的速度。

液相动量守恒方程为：

式中 ∇P——液相的静压梯度；

μ——液相的动力黏度；

Ffpi——固相对液相作用力的总和；

ΔVcell——流体域网格单元的体积。

颗粒与流体的相互作用是通过相间双向耦合实现的。如图1所示，在一个时间步长内，CFD求解器计算液相流场并将其传输至DEM求解器计算液相对颗粒的作用，从而计算更新颗粒运动信息，最后将颗粒运动信息传回CFD求解器，完成一个时间步长内的双向耦合计算。

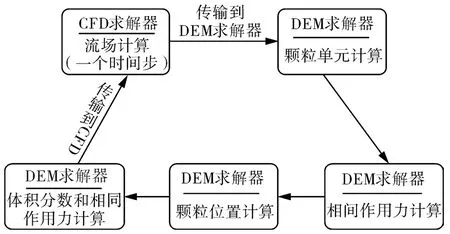
图1 CFD-DEM耦合的流程Fig.1 The coupling process of CFD-DEM

1.2 磨损模型

根据颗粒与壁面接触方式的不同，颗粒对离心泵过流部件的磨损分为碰撞磨损和摩擦磨损［17］。碰撞磨损是指固体颗粒直接撞击壁面导致的磨损，本文选用Oka模型［18］计算。摩擦磨损指颗粒沿过流部件表面作切向摩擦产生的磨损，选用 Archard 模型［19］计算。

2 数值模拟方法的验证

2.1 模型和网格

研究的模型泵为扬程H=8 m，流量Q=20 m3/h，转速n=1 450 r/min，比转速ns=83的单级单吸离心泵。叶轮的主要几何参数有叶片数Z=5，进口直径D1=80 mm，叶轮外径D2=164 mm，进口安放角β1=12°～21°，出口安放角β2=27°，包角φ=110°；蜗壳的主要几何参数为基圆直径D3=178 mm。

流场的计算域如图2所示。通过网络无关性分析，兼顾计算效率与准确性，选取叶轮和蜗壳网格数为489 031，计算结果如图3所示。

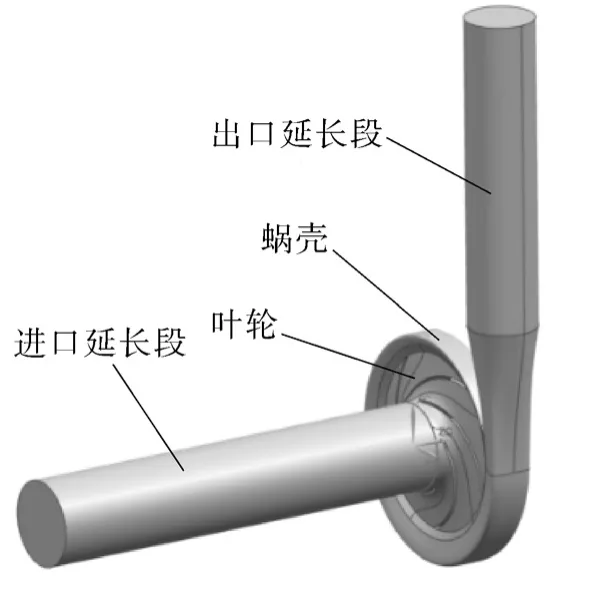
图2 离心泵水体三维Fig.2 Three-dimensional diagram of the fluid domain in the centrifugal pump

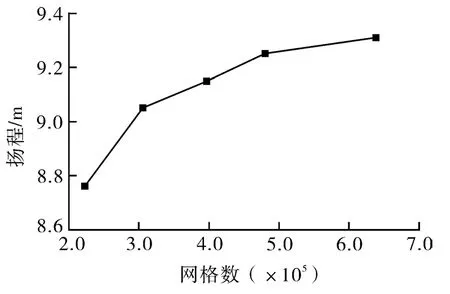
图3 网格无关性分析Fig.3 Grid independence analysis

2.2 模拟设置

设置叶轮每旋转1°计算一次，则时间步长为1.494×10-4s，总模拟计算时间为 0.206 9 s，即叶轮旋转5圈。固相为粒径2.5 mm，体积分数10%的球形颗粒，颗粒与壁面的具体材料参数见表1。

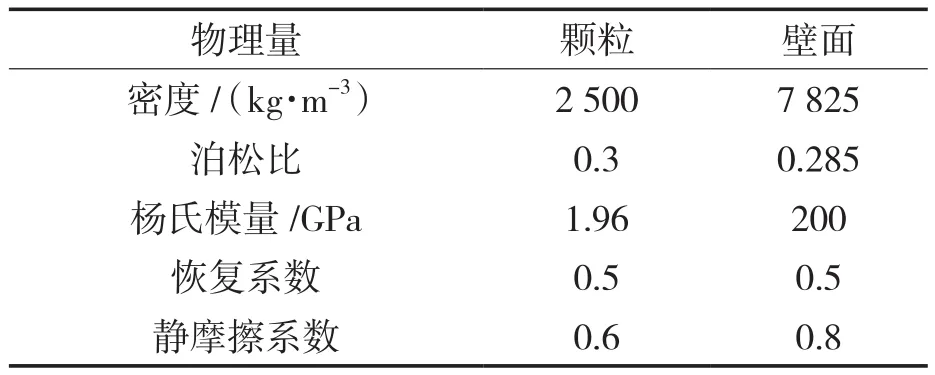
表1 颗粒和壁面的材料参数Tab.1 Material parameters of particles and wall

2.3 外特性计算结果及验证

进行了清水工况下的性能试验，数值模拟和试验测试结果如图4所示，扬程计算的最大误差为5.1%，这表明本文采用的数值模拟方法具有较高的计算精度。

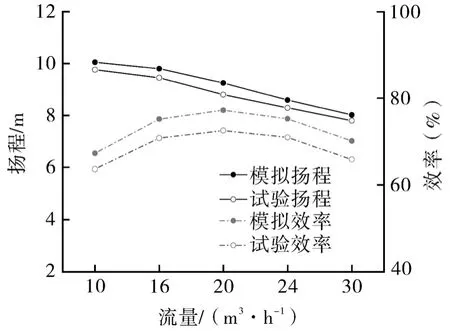
图4 试验与数值计算结果对比Fig.4 Comparison of experimental and numerical calculation results

3 模拟结果与分析

3.1 出口安放角对叶轮磨损特性的影响

图 5 示出β2=18°，27°和 35°时叶轮盖板与叶片的平均磨损率分布。当β2从18°增大至27°时，叶片吸力面的磨损加剧，这是由于吸力面中间位置颗粒聚集，颗粒相对运动速度较大，颗粒对壁面的撞击频率更高，导致该区域磨损最为严重；β2增大至35°时，叶轮的最大平均磨损率降低36%，叶片压力面及其对应的盖板位置磨损程度明显减轻，这是由于颗粒聚集现象消失，叶轮出口附近的颗粒逐渐偏离压力面。

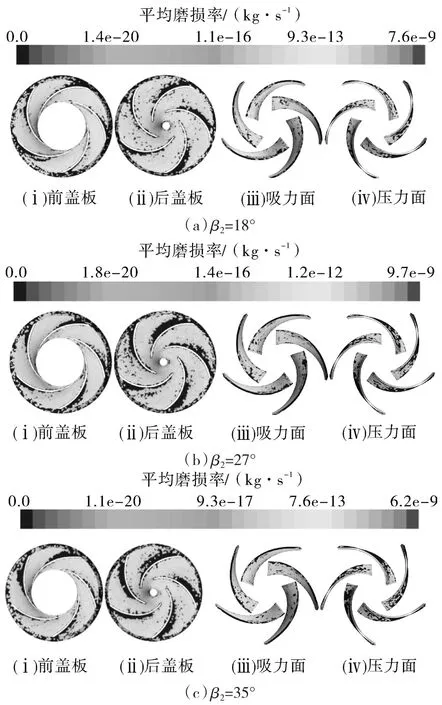
图5 不同出口安放角叶轮的平均磨损率分布Fig.5 Average wear rate distribution of impellers with different outlet angles

接触次数定义为计算时间段内颗粒与壁面的碰撞次数，碰撞产生的法向接触力与切向接触力的合力即为颗粒与壁面的接触力，接触次数与接触力是影响磨损程度的主要因素。图6示出β2=18°，27°和 35°时颗粒与叶轮壁面的接触力三维散点，接触次数分别为184，178，116次。β2=18°时的接触次数最多，β2=27°时产生的接触力的范围最大，最大接触力达到5.2 N，是β2=35°时最大接触力的10倍，这是β2=27°时叶轮磨损最严重的主要原因。

图6 不同出口安放角时接触力三维散点Fig.6 3D scatter diagram of the contact force with different outlet angles

不同出口安放角叶轮的最大平均磨损率见表2。可以看出，随着β2增大，叶轮的最大平均磨损率先增大后减小。结合图5可以看出叶轮的平均磨损率分布极不均匀，因此最大平均磨损率的变化能够反映叶轮磨损特性的变化规律。

表2 不同出口安放角叶轮的最大平均磨损率Tab.2 Maximum average wear rate of impellers with different outlet angles

3.2 进口安放角对叶轮磨损特性的影响

图7示出不同进口安放角叶片吸力面平均磨损率分布。结合图5（b）可以看出，随着β1增大，叶片在吸力面中间位置的磨损区域逐渐从叶片中间位置向进口边延伸。

图7 不同进口安放角叶片的平均磨损率分布Fig.7 Average wear rate distribution of blades with different inlet angles

图 8 示出β1=12°～21°，20°～29°和 27°～36°时颗粒与叶轮壁面的接触力三维散点。随着β1的增大，颗粒与叶轮的接触点逐渐向叶轮进口延伸，接触次数分别为113，211，214次，接触次数不断增多，但接触力先增大后减小。

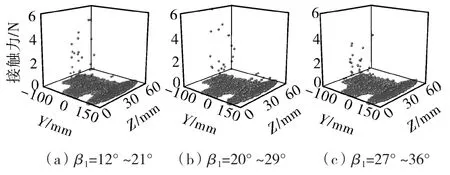
图8 不同进口安放角时接触力三维散点Fig.8 3D scatter diagram of the contact force with different inlet angles

不同进口安放角时叶轮的最大平均磨损率见表3。可以看出，随着β1的增大，叶轮的最大平均磨损率先增大后减小，在β1=20°～29°时，叶轮的磨损程度最严重。因此，相较于接触次数，接触力的大小对叶轮磨损程度的影响更大。

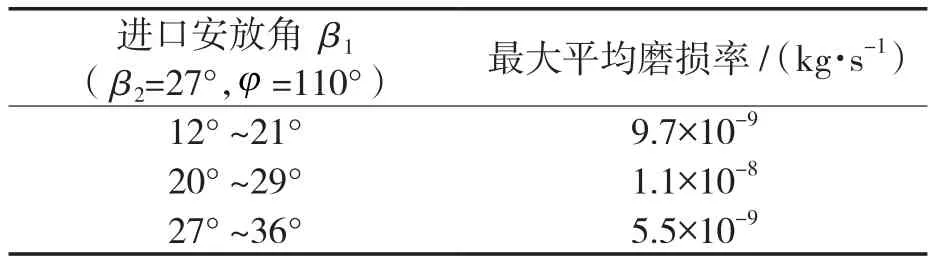
表3 不同进口安放角叶轮的最大平均磨损率Tab.3 Maximum average wear rate of impellers with different inlet angles

3.3 包角对叶轮磨损特性的影响

图9示出不同包角叶片吸力面平均磨损率分布，结合图5（b）可以看出，随着φ增大，磨损严重区域逐渐相叶片吸力面中间部位偏移，这是由于流道增长，叶片更加弯曲，影响了颗粒运动状态，导致磨损严重区域位置改变，磨损严重区域面积减小。

图9 不同包角叶片的平均磨损率分布Fig.9 Average wear rate distribution of blades with different wrap angles

图10示出φ=90°，110°和 130°时颗粒与叶轮壁面的接触力三维散点，接触次数分别为164，174，156次，φ=110°时接触力最大，导致了叶轮磨损程度最严重。

图10 不同包角时离心泵内接触力三维散点Fig.10 3D scatter diagram of the contact force of the pump with different wrap angles

不同包角叶轮的最大平均磨损率见表4。可以看出，随着φ的增大，叶轮的最大平均磨损率先增大后减小，在φ=110°时，叶轮的磨损程度最严重。

表4 不同包角叶轮的最大平均磨损率Tab.4 Maximum average wear rate of impellers with different wrap angles

3.4 叶轮抗磨损性能的优化

采用Box-Behnken Design（BBD）试验设计方法进行响应面优化设计，因素A：进口安放角β1，因素B：出口安放角β2，因素C：叶片包角φ，由于进口安放角为线性变化，故取线性变化的最大值作为因素的水平。试验设因素水平见表5。

表5 BBD各因素水平Tab.5 The factor level table of BBD

以平均磨损率作为优化的目标函数，以效率提高1.5%作为约束条件，对β1，β2和φ进行优化。建立的数学模型如下：

式中 Y——平均磨损率；

ηi——第i组效率；

η0——原模型效率；

xim——影响因素下限；

xi——叶片主要影响参数；

xin——影响因素上限。

经过寻优求解获得最优参数组合的叶轮模型，优化前后叶轮参数对比见表6。与原方案相比，扬程满足设计要求，效率略有提升，磨损严重区域的最大平均磨损率从9.7×10-9kg/s降低到6.5×10-9kg/s。

表6 设计参数对比Tab.6 Comparison of design parameters （°）

由图11与图5（b）对比可以看出，优化后的前后盖板与叶片吸力面中间位置磨损程度明显减轻，叶轮抗磨损性能得到显著提升，证明优化方法有效可靠。

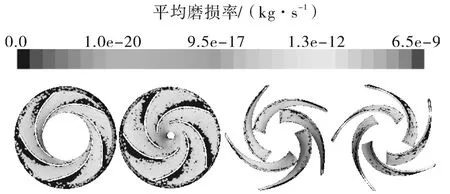
图11 优化后模型的叶轮平均磨损率分布Fig.11 Average wear rate distribution of optimized impeller

4 结论

（1）叶片出口安放角、进口安放角和包角显著影响了离心泵叶轮的磨损特性。出口角为27°时，叶片吸力面中间位置磨损最严重，随着出口安放角的增大，叶片吸力面中间位置和压力面出口位置磨损明显改善；随着进口安放角的增大，叶片的磨损严重区域从叶片中间部位向进口方向延伸；随着包角的增大，磨损严重区域向叶片吸力面中间部位偏移。

（2）经过响应面优化，离心泵叶轮的最大平均磨损率从 9.7×10-9kg/s降低到 6.5×10-9kg/s，叶轮的抗磨损性能明显改善。