基本数论问题的可视化证明方法研究与实践*

刘新宇 张艳硕 常万里

北京电子科技学院，北京市 100070

1 引言

数论［1］作为纯粹数学的重要分支之一，被誉为数学的皇冠，主要研究方向是整数，特别是正整数的性质以及代数方程的整数解等内容。数论问题探究是数学研究中十分重要的领域，一直以来，对古老的若干数论问题的深入研究成为了现代数学发展的重要推动力之一，数论问题及其结论在计算机、密码学、物理学等领域都有着广泛的应用。 基本数论问题作为数论研究中的基本内容，是数论研究的基石，对于数论基本问题本身及其证明方法的研究在数论研究中具有实际意义。

可视化研究［2］是当前国际上的热点问题，在数学、物理学、化学等学科领域，可视化作为一种便于理解的形式广泛应用于研究过程以及研究结果中。 随着教学媒体的发展和学习理论的发展可视化教学的形态、特性和内涵都发生了巨大变化，可视化教学和可视化教学研究也出现新的发展和趋势。 在数学领域，可视化的研究内容主要包括：数学问题可视化、数学猜想可视化、数学理解可视化与数学推理过程可视化。 在数学问题实例中，往往一个数学对象蕴含着多个要素，利用可视化技术能够展示出同一数学对象不同方面的特征，从而达到从多个维度来分析思考数学对象的目的。

数论同几何有着十分密切的联系［3］，许多基本数论问题都存在几何方法的描述或证明，如毕达哥拉斯游程问题、巴塞尔问题、费马大定理［4］等。 本文从毕达哥拉斯游程问题和巴塞尔问题出发，以托勒密定理为范例，通过对这些问题本身及其证明方法的研究，探索基本数论问题的可视化证明方法。 基于当前可视化证明存在的优势与特点，从可视化证明内容和可视化证明方法两个方面探索基本数论问题的可视化证明，得到一种适用于基本数论问题的可视化证明方法，降低可视化证明难度，提高基本数论问题可视化证明的理解能力与表达效果。

2 基本数论问题

基本数论问题是数学发展的动力，科学发现的先导，促进了数学理论的发展，也促进了数学方法的研究。 纵观历史上的一些著名数论猜想，如哥德巴赫猜想、毕达哥拉斯游程问题、巴塞尔问题等等，这些基本数论问题对数学的研究和发展，起了积极的推动作用。 正是无数数学家们的猜想，数学科学才发展到当今的现代数学，可以说，数学猜想是现代教学的必然要求，基本数论问题是数学发展史上的重要成就。

2.1 毕达哥拉斯游程

毕达哥拉斯游程［5］（Pythagorean Runs）问题是对毕达哥拉斯定理的拓展，使毕达哥拉斯定理中的等式能够囊括更多的数字。

毕达哥拉斯定理［6］若一个三角形为直角三角形，那么它的直角边a、b和斜边c满足：a2＋b2＝c2。

2.2 巴塞尔问题

巴塞尔问题［7］（The Basel Problem）是由数学家皮耶特罗·门戈利1644 年提出的数论问题。其问题可简单概括为求所有自然数平方的倒数和，即计算：

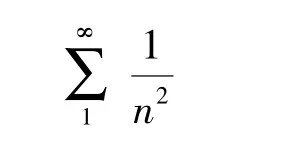
莱昂哈德·欧拉（Leonhard Euler）通过泰勒级数展开法求出了巴塞尔问题的准确值：

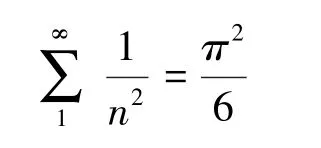
欧拉于1735 年公布，但当时他的证明还不是十分严密，真正严密的证明在1741 年给出。

2.3 托勒密定理

托勒密定理（Ptolemy′s theorem）是欧几里得几何学中的一个定理，以古希腊亚历山大后期重要数学家、 天文学家和地理学家托勒密（Claudius Ptolemy）的名字命名。 托勒密在其著作《天文学大全》（又称《数学汇编》、《大汇编》）13 卷中为了推导两角之和、差的正弦公式计算弦表，证明的一个引理，后人把这一引理称作托勒密定理。

托勒密定理［9］圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

3 基本数论问题的理论证明

3.1 毕达哥拉斯游程的理论证明

毕达哥拉斯游程作为毕达拉斯定理的拓展，与几何问题有着密切的联系。 从几何角度对毕达哥拉斯游程问题进行分析，能够得到一种不同于代数证明的证明方法。 从最初的32＋42＝52开始，其等式内容便可以表示为图1：

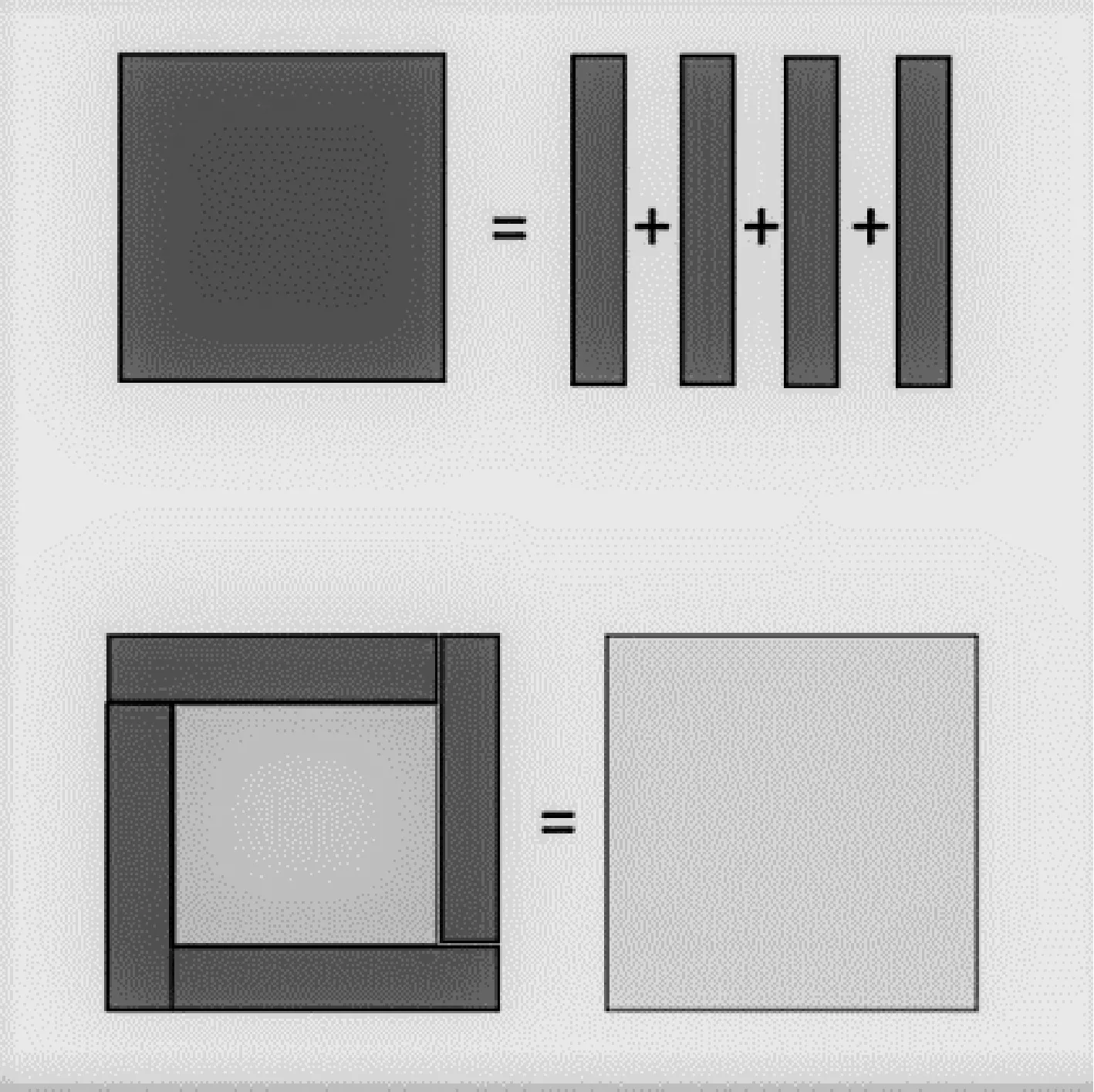
图1 32 ＋42 ＝52 的几何表示

图1 将等式32＋42＝52转化为两个边长分别为3、4 的正方形面积之和等于边长为5 的正方形面积。 通过将边长为4 的正方形分割为四个长为4，宽为1 的四个长方形，使得在面积总和不变的情况下与变长为3 的正方形进行组合，构成边长为5 的正方形，这一几何表示结果无疑是正确的。 基于这一思路，可以将毕达哥拉斯游程问题所包含的所有等式进行几何表示，其基本思路为将等式两边多个不同边长的正方形进行分割、组合，使等式两边多个不同边长的正方形最终转化为两个边长相等的正方形，可验证其面积相等，即得出等式成立的结论。

3.2 巴塞尔问题的理论证明

除欧拉的泰勒级数展开法外，巴塞尔问题存在多种证明方法，如：数学分析证明法、复分析证明法等［7］，这里要介绍的是一种几何证明法［8］。

首先，如图2，构造圆A，令圆A 周长为2。再以点B 为圆心，OB 为半径构造圆B，过点B 做OB 垂线交圆B 于点P′、P″。 存在等量关系：

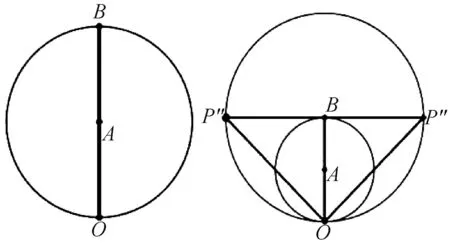
图2 构造图形

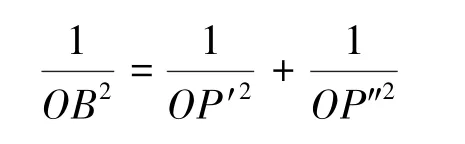
接着，如图3，在圆B 的基础上，以OB 延长线上点C 为圆心，OC 为半径，构造圆C，然后分别过点P′、P″做OP′、OP″垂线交于圆C 于点Q′、Q″、Q‴、Q″″，得到：

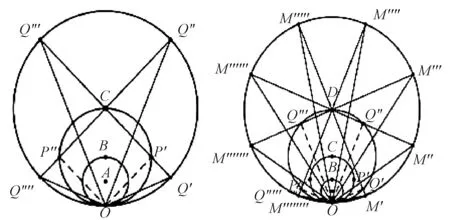
图3 四次重复操作后的结果

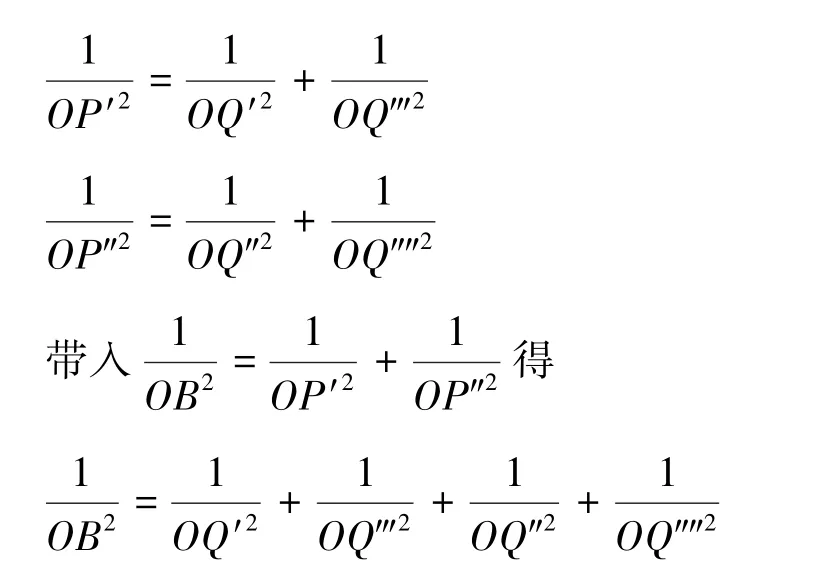
重复上述步骤，在OB 延长线上取一点做圆，并令圆的半径是已有最大圆半径的2 倍。 之后再取上一步在最大圆上点，做过这些点与O连线的垂线，交已有最大圆上点O 点右侧点从左至右依次记为ni（i ＝1、2、3...），O 左侧点从右至左依次记为ni（i ＝－1、－2、－3...），并记点O为n0。 可以预见到，当我们重复这一步骤足够多时，所有点趋近于在一条直线。

将这条直线作为数轴，令n0为零点。

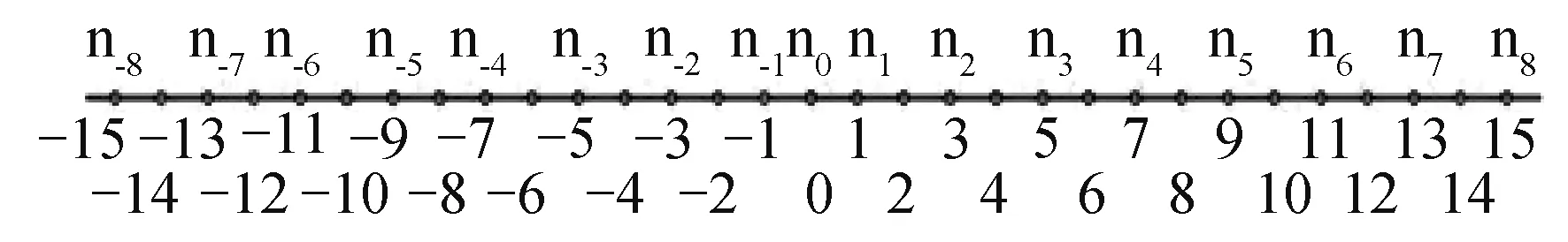
图4 数轴

记点ni到零点的距离为di，此时有：

3.3 托勒密定理的理论证明

托勒密定理的证明方法有很多种，如几何证明法［9］、三角证明法［10］、无字证明法［11］等。 这里介绍无字证明法。

以图5 为例。

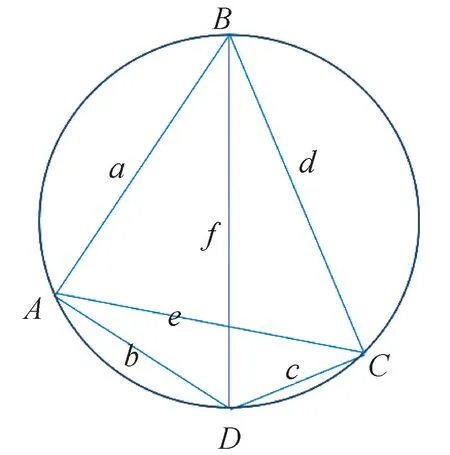
图5 无字证明示例

证明过程如下：

将ΔADC每条边乘上a， 得到新的三角形ΔA′D′C′，如图6 所示。

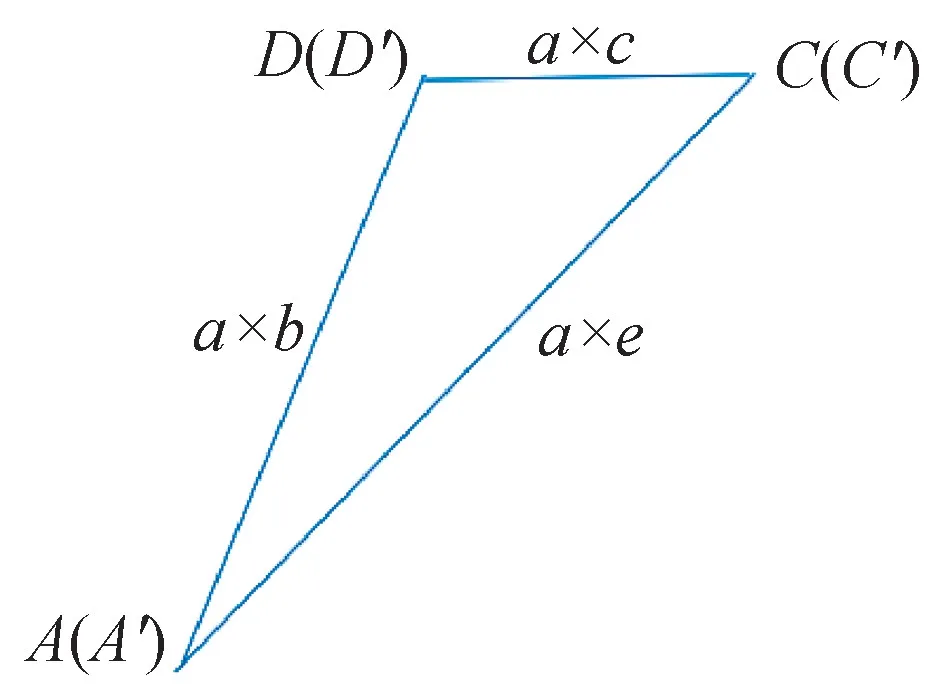
图6 三角形A′D′C′

如果想让ΔA′D′C′与ΔABC经过放大后的ΔA′B′C′构成平行四边形，则需要将ΔABC各边乘上b，得到图7 所示。

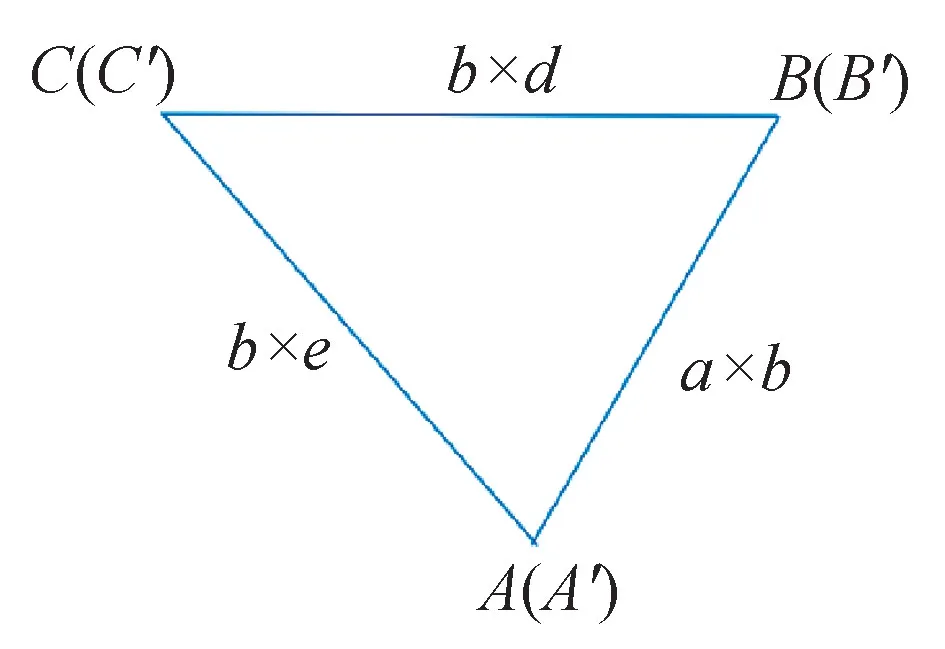
图7 三角形A′B′C′

再将ΔABD各边乘上e， 得到ΔA′B′D′各边，如图8 所示。

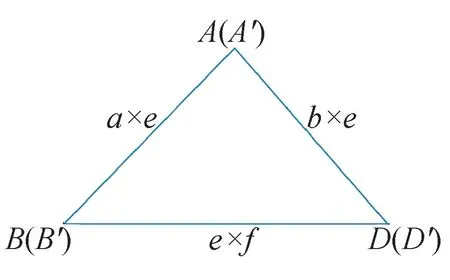
图8 三角形A′B′D′

将经过如上操作后的图形，由于在圆中同一根弦对应的不同侧的圆周角之和为180°， 所以∠B′＋∠D′＝180°，又因为A′B′＝A′D′，满足有一组对边平行且相等的条件，所以可以组合成图9 中的平行四边形。

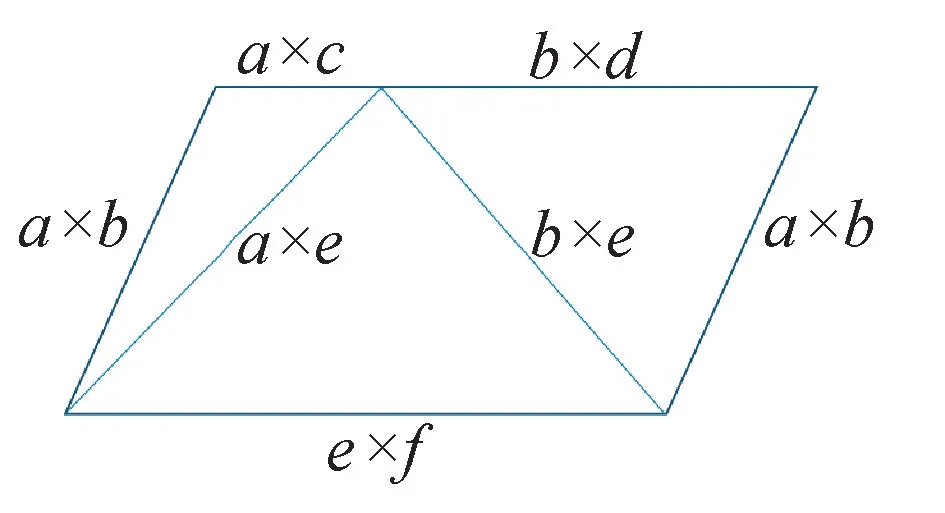
图9 组合平行四边形

因为在ΔA′B′D′中，A′B′＝a ×e，A′D′＝b ×e， 且有∠BAD ＋∠BCD ＝∠BAD ＋∠BCA ＋∠DCA ＝∠B′A′D′ ＋∠B′C′A′ ＝180°。

所以ΔA′D′C′、ΔA′B′D′、ΔA′B′C′可以组合为一个平行四边形，如图9 所示。

由平行四边形的性质可知：a ×c ＋b ×d ＝e× f。 托勒密定理得证。

4 可视化证明方法的相关研究成果

可视化是利用计算机图形学和图像处理技术，将数据转换成图形或图像在屏幕上显示出来，并进行交互处理的理论、方法和技术。 可视化与可视化教学因其本身具有的优势成为了教育研究者所关注的热点，其在多个学科领域都有广泛的应用。 在数学领域，可视化的研究内容主要包括：数学问题可视化，数学猜想可视化，数学理解可视化，数学推理过程可视化。 下面将从可视化证明形式、可视化证明工具和可视化证明的优势与不足三个方面进行介绍。

4.1 可视化证明形式

（1）交互式证明

交互式证明方法通常借助某一种软件实现，通过代码或其他方法设计可视化界面，借助软件自身的功能或自己设计的功能，以改变各项参数的方式对可视化内容进行修改，从而达到可视化证明的目的。

（2）非交互式证明

非交互式证明方法可以分为静态可视化和动态可视化两种。

静态可视化使用图形将数学证明中的证明过程及计算结果以静态图形的形式显示出来，形成对过程和结论的直观感受，从而发现复杂数据和过程中的内在联系和规律［12］。

动态可视化将通俗易懂的静态语言同软件生成的动画演示相结合，区别于静态可视化，动态可视化证明过程是连续的，体现出来的证明思维过程更加直观，能够更好的体现证明过程中的思维方法。

4.2 可视化证明工具

目前可视化证明工具种类繁多，本文选取其中一部分进行介绍。

（1）MATLAB 软件是由美国MathWorks 公司推出的用于数值计算和图形处理的科学计算系统环境。 现在的MATLAB 已经成为了一种具有广泛应用前景的全新的计算机高级编程语言，有人称它为“第四代”计算机语言，它在国内外高校和研究部门正扮演着重要角色。 可以预见，在科学运算、自动控制与科学绘图等领域MATLAB 语言将长期保持其独一无二的地位［13］。

（2） Maxima［14］的前身是DOE-Macsyma。DOE-Macsyma 是由麻省理工学院（MIT）在美国能源部的支持下于60 年代末创造的一种CAS，它是用LISP 实现的。 Macsyma 在当时是非常创新的软件。 现在流行的商业计算机代数系统软件Maple 及Mathematica，都是受到Macsyma 的启发而设计出来的。

（3）Manim［15］是基于Python 的数字动画引擎，支持Latex 公式的输入。 其作为近几年新出现的可视化工具，由于出色的动画渲染效果以及出色的数学公式支持，成为了数学可视化工作领域一款新的工具。 不同于MATLAB 等商业软件，Manim 作为一款开源工具，由Manim 社区进行维护和更新，其使用完全免费。

除以上介绍的可视化工具外，Excel、Plotly、Tableau 等工具在可视化工作种均存在较多使用，但由于适用范围以及可视化效果等方面的原因在这里不展开介绍。

4.3 可视化证明的优势与不足

可视化的证明方法优势在于将一个数学对象蕴含的多个要素通过可视化技术展示出来，从而达到从多个维度来分析思考数学对象的目的。同时避免了传统证明方法中繁多的公式说明和复杂的数学计算，将数学问题的证明过程以简单直观的方式进行展示，有效降低了数学问题证明过程抽象性、理解难度和学习成本［16］。

可视化证明的不足之处体现在两个方面：一是可视化内容制作存在一定难度。 目前被广泛使用的众多可视化工具均存在较高的学习成本，可视化内容的制作存在较高门槛；可视化证明制作内容难以组织，实际可视化证明效果难以达到预期。 二是可视化证明这一形式相较于传统证明方法存在天然不足。 可视化证明往往采用过于直观的展示方式，在证明过程中以图像的变换代替了繁多的公式和复杂的计算，使得证明过程中的数据计算及相关逻辑说明丢失。

5 基本数论问题的可视化证明方法

在谈到可视化的教学应用问题时，我们考虑的并不仅是学生个体使用可视化证明方法时学习效果的提升，还必须考虑在教学过程中如何运用的问题。 我们基于基本数论问题的分析及可视化证明方法存在的优势与特点，从毕达哥拉斯游程问题、巴塞尔问题为代表的基本数论问题出发，给出了一种适用于基本数论问题可视化证明的基本方法和思路。

5.1 基本数论问题的可视化证明内容

基本数论问题可视化证明内容的确定是基本数论问题可视化证明实现过程中极为重要的一环，对需要可视化的内容的确立直接影响了可视化证明在表达上的连贯性和理解上的难易程度［17］。

从前文所列举的基本数论问题可以看出，基本数论问题大都具有几何上的描述及证明。 以巴塞尔问题为例，本文所列举的几何证明法先将巴塞尔问题与圆相联系，再从特定延长线对圆周的取点着手，对巴塞尔问题进行分析，最终得到巴塞尔问题的一个明证。 基于基本数论问题的几何描述及几何证明方法，我们能较为容易的组织起基本数论问题的可视化证明内容，其主要分为以下三个方面：

（1）证明内容描述

对于证明过程的描述要力求简洁、准确，避免在证明中出现不准确的描述，使读者无法快速了解可视化证明的内容。 在证明内容描述上力求做到使用较少的图像描述问题，必要时辅以文字或其他说明。 以毕达哥拉斯游程问题为例，前文中对于32＋42＝52这一等式的图像描述，除必要的边长为3、4、5 的三个正方形及其联系外，不再含有多余要素。 这不仅能使读者快速理解相关内容，也能避免其在多余要素影响下产生误解。

（2）证明过程体现

可视化证明过程是可视化证明内容中极为重要的一环，其难点在于证明思维连贯性和严谨性于可视化证明中的体现［18］。 解决这一难点，需要在可视化证明实现之前确定可视化证明关键内容，关键内容的确定须遵守原则：一是关键步骤不可省略。 对于证明过程中的关键性步骤，影响到证明逻辑连贯性的一定不能省略。 二是不需要说明的步骤一律不作展示和说明，证明内容做到简洁，只有在不易理解的地方加以说明。以巴塞尔问题为例，巴塞尔问题的几何证明方法关键在于数轴的构造，而数轴的构造是一个连续的思维过程。 在可视化证明中，取点过程的连贯性和取点的严谨性都需要得到体现，否则会使读者难以理解证明过程。

（3）证明结果展示

证明结果的展示要做到简洁、清晰、易理解，避免出现证明结果展示难以理解或无法理解的情况。 证明结果为图像的要以清晰、直观的方式将结果呈现，必要的标注和说明不可缺少；证明结果为表达式的，表达式的变化过程一定要清晰呈现，避免“跳步”，让人难以理解。 不同的证明内容所要展示的证明结果存在一定差异，如何选取证明结果的展示形式需要根据具体问题进行具体分析。 以毕达哥拉斯游程问题为例，其证明结果存在两种形式：图形和等式。 单一的图形或者等式其本身已经具有较好的展示效果，但更优的做法是将两者相结合，以图形的直观性辅以等式的逻辑性，从而达到清晰的呈现效果。

5.2 基本数论问题的可视化证明方法

基本数论问题的可视化证明方法主要有以下“三化”特点［19］：

（1）结构化

对基本数论问题的可视化证明进行结构划分，有助于基本数论问题可视化证明内容的完成。 对划分后的基本数论问题可视化证明内容使用模块化的设计方法，逐层设计可视化证明内容，能够有效提高可视化证明内容的完成效率，降低完成难度。

（2）图示化

基于结构化对基本数论问题可视化证明内容的划分，对证明内容进行图像展示。 图示化所制作图像需要清晰简洁，画面元素不能过于复杂，在画面设计过程中力求做到画面元素一目了然，尽量避免一个画面中同时包含多个步骤，从而造成理解上的困难。

（3）注释化

纯图像的说明虽然足够直观，但是在理解上存在一定难度，通过适当地添加一些注释能够有效避免可视化证明中纯图像的弊端。 在对基本数论问题的可视化证明中，注释主要包括图像注释、文字说明。 图像注释可以将变化后的图像同原图像联系起来，形成逻辑上的连贯性；文字说明则能展示不方便以图像形式表达的内容和说明，能够与图像和图像注释形成良好的补充关系［20］。

6 可视化证明方法应用

前文中通过对毕达哥拉斯游程问题、巴塞尔问题和托勒密定理为代表的基本数论问题进行研究，给出了基本数论问题的可视化证明方法，接下来展示以托勒密定理为例进行的可视化教学方法实际应用。

6.1 托勒密定理的可视化证明内容

托勒密定理的可视化证明内容基于托勒密定理的无字证明方法提出，其证明内容及关键步骤在前文中已经说明，在这一部分不作赘述。 基于这一证明方法的可视化证明内容主要包括：

（1）托勒密定理的说明

（2）无字证明法中三角形的变换过程

（3）无字证明法中三角形组合成平行四边形的具体方法

（4）从组合平行四边形中得出托勒密定理

6.2 托勒密定理的可视化证明方法

（1）结构化

托勒密定理的可视化证明共有三个部分［21］。 第一个部分为托勒密定理内容展示，以可视化的方式展现托勒密定理。 第二个部分为证明过程的演示，通过对几何图形的变换完成对托勒密定理的证明。 第三个部分是证明结果的展示，对第二部分中图形变换的结果进行总结，清晰的展示出托勒密定理的可视化证明结果。

（2）图示化

第一个部分画面由两部分组成，托勒密定理的前提描述和托勒密定理的结论描述。 托勒密定理的前提描述由一个圆、圆的内接凸四边形以及该四边形的两条对角线构成。 托勒密定理的结论由两对对边乘积的和等于两条对角线的乘积这一等式进行描述。

第二个部分是对圆的内接四边形所包含三角形的变换和组合，通过对三角形的旋转以及缩放构建出证明所需要的等量关系，从而达到证明托勒密定理的目的。

第三个部分是对证明结果的总结。 由于第二部分中对托勒密定理的证明结果以图像的形式展现，不容易将其与托勒密定理的文字说明所联系起来。 所以在这一部分中再次重新以文字的形式表述托勒密定理，增强可视化证明与托勒密定理文字说明的联系，使得可视化证明内容更加容易理解。

（3）注释化

在对托勒密定理的可视化证明中，注释主要分为两个部分， 一是图像注释， 二是文字说明［22］。

图像注释是对证明过程中所出现的图像的说明和标注，能够帮助理解证明过程中所出现的各个图像的意义和联系。 在对托勒密定理的可视化证明中，图像注释主要是对几何图形的标注，这一注释有助于将证明过程中变化后的图形与原图形联系起来。

文字说明是对图像说明的补充，用于将那些不适用图像表示的内容以文字的形式展示。 在对托勒密定理的可视化证明中，托勒密定理的原文用图像表示就不便于理解，于是在证明过程中辅以文字说明进行补充，帮助理解托勒密定理的内容。

6.3 托勒密可视化证明工具

可视化证明有着众多的工具，Excel、Plotly、Tableau、Manim 等均是被使用较多的可视化工具［23］。 Excel、Plotly、Tableau 常被用来进行数据可视化，其在数据处理和分析方面具有明显优势，但是这些可视化工具并不适用于托勒密定理的可视化证明。 相较于这些可视化工具，Manim在对数学方法的实现中具有其独特的优势。

Manim 是基于Python 的数字动画引擎，支持Latex 公式的输入，可以很好的表达数据在可视化结果中的含义与相互关系，对数学方法的实现过程的可视化效果相当出彩。 选择Manim 作为本文可视化演示的工具，有效的提升了证明过程的直观性［24］。

6.4 托勒密定理的可视化证明结果

现将可视化证明结果进行如下展示：

（1）托勒密定理说明

图10 为托勒密定理的展示，以文字和图形结合的方式清晰的展示托勒密定理的主要内容，以便于接下来对托勒密定理进行证明。

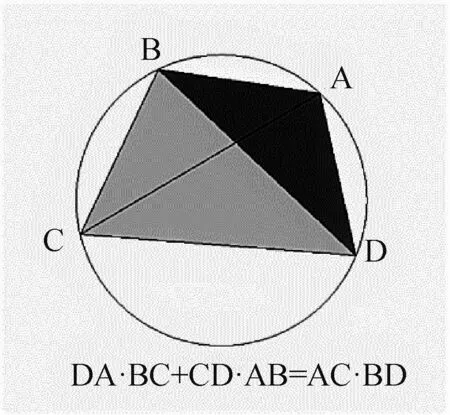
图10 托勒密定理内容展示

（2）托勒密定理证明

图11 用灰色和黑色两种颜色将接下来需要进行变化的两个三角形标识出来，以便于在图12、图13、图14 的变化中区分两个三角形。

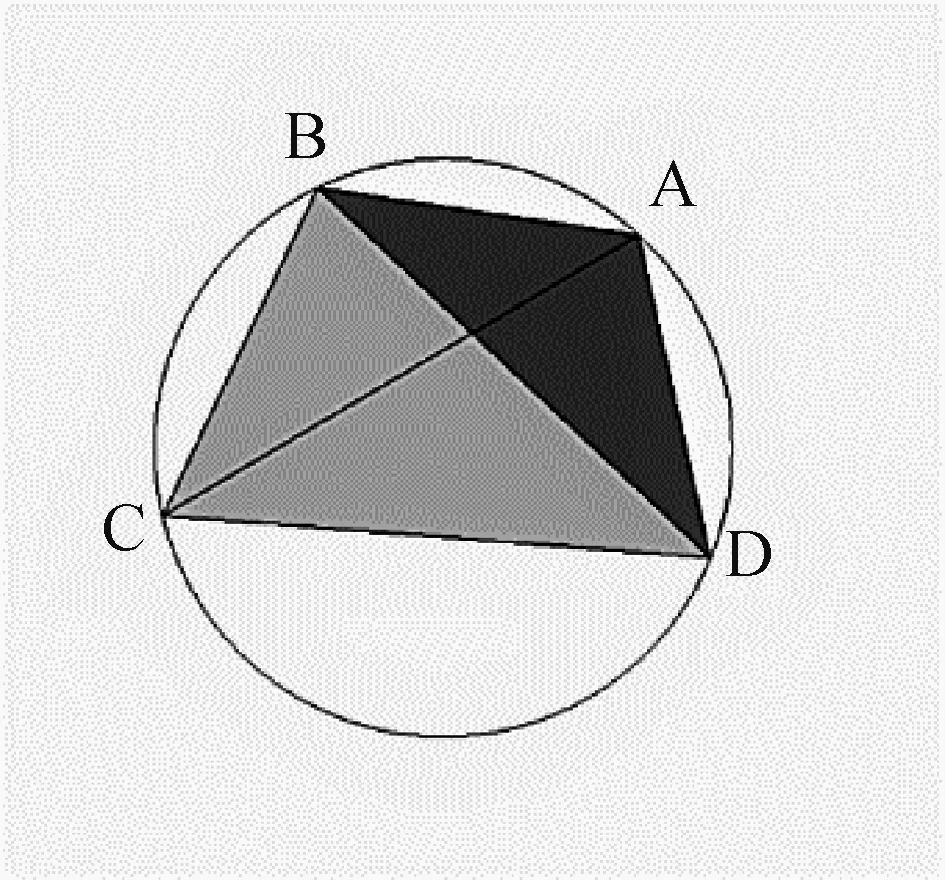
图11 标识后的两个三角形

将图11 中的灰色和黑色两个三角形绕B 点分别按逆指针和顺势针旋转一定角度达到图12所示位置。

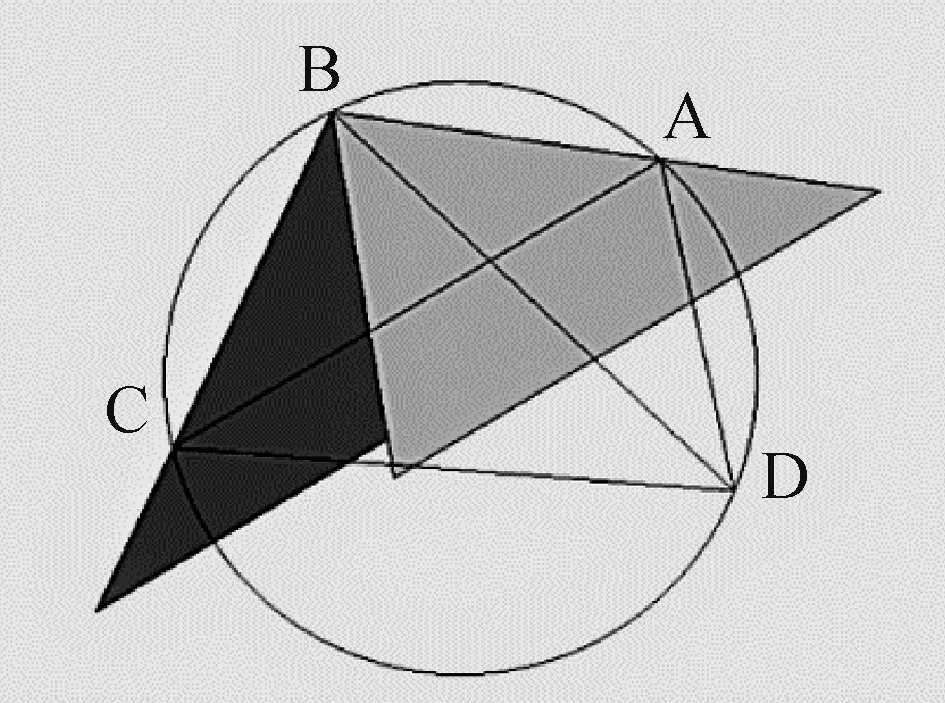
图12 旋转后的三角形位置

接下来将灰色和黑色两个三角形分别以BA、BC 为轴翻转到图13 中所示位置。

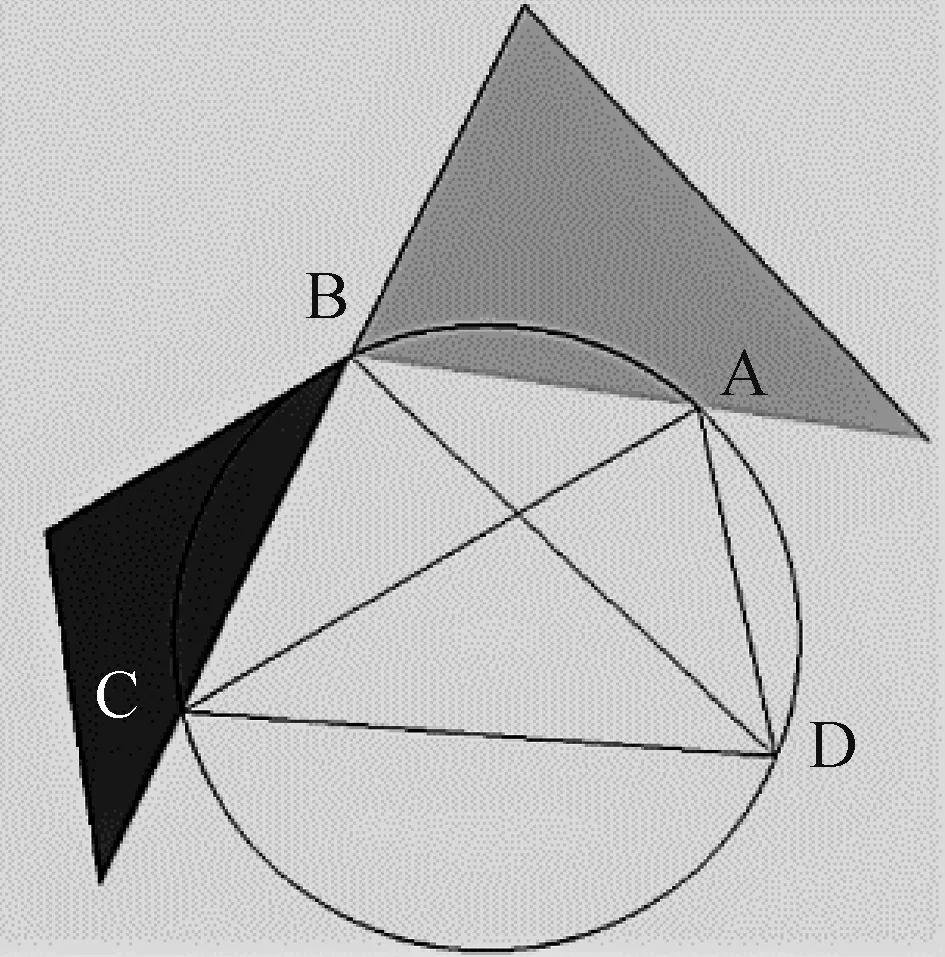
图13 翻转后的三角形位置

再次将灰色和黑色两个三角形进行位置上的变换达到如图14 所示的位置，可以看到这时两个三角形所组成的图形已经有了平行四边形的形状。

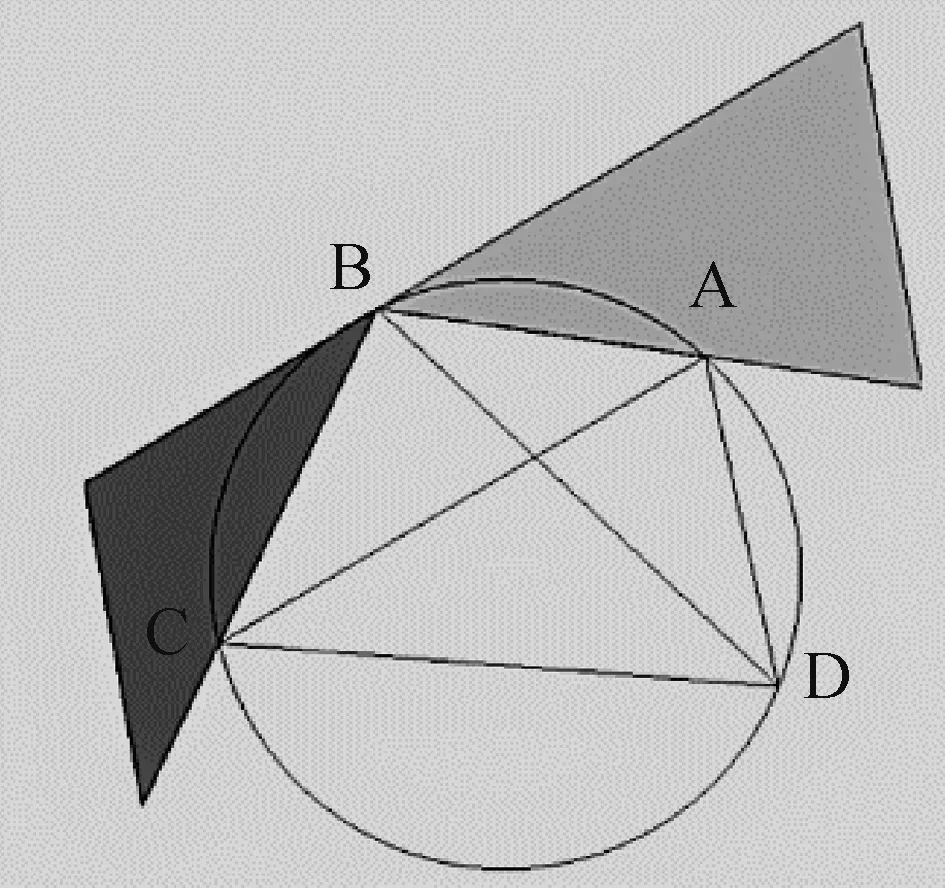
图14 经过变换后的三角形位置

（3）证明结果展示

图15 将达到合适相对位置的两个三角形以及这两个三角形所夹三角形各自按照一定比例放大，组合成为一个平行四边形，根据平行四边形的几何性质证得托勒密定理。

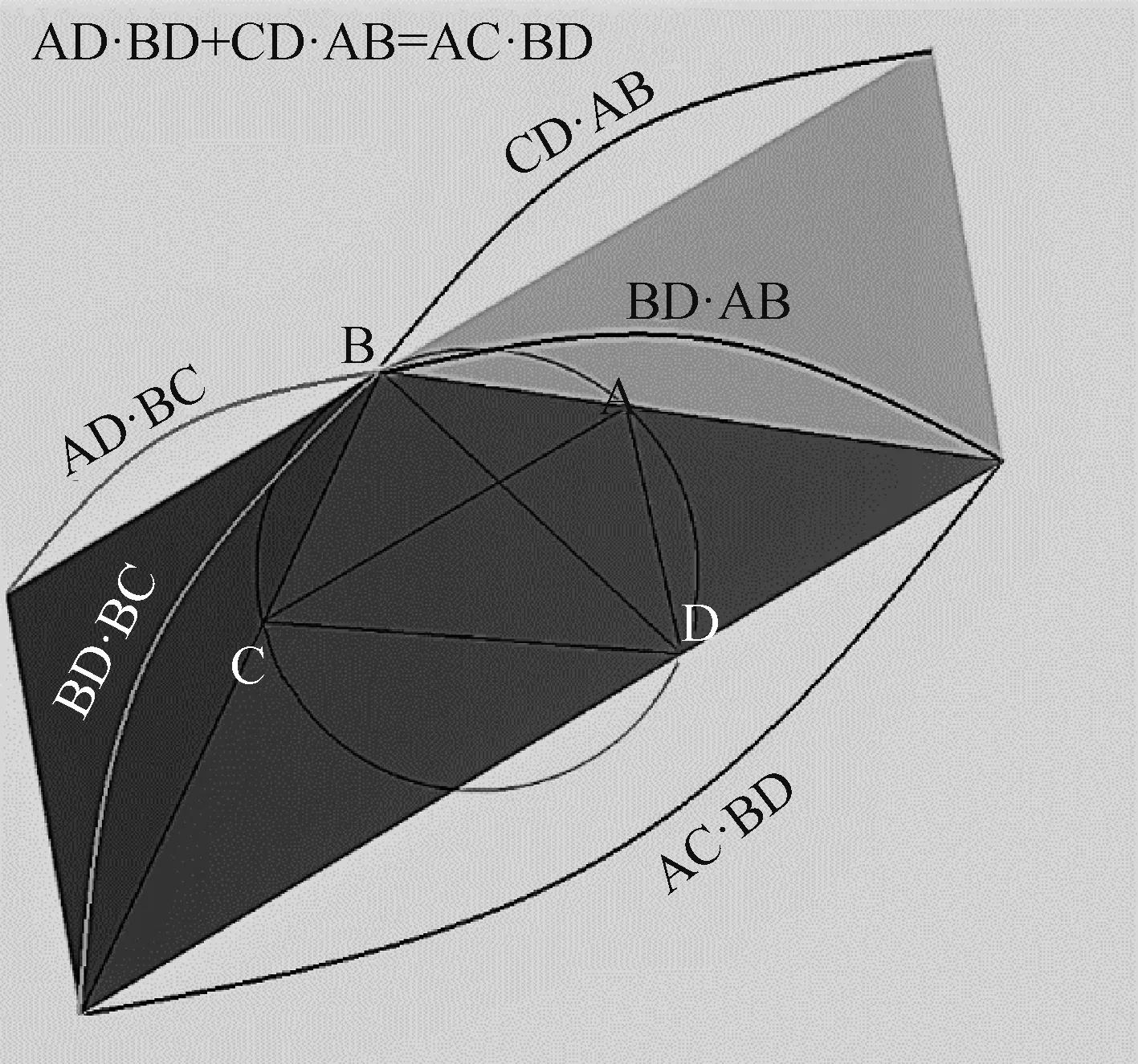
图15 按比例放大后构成的平行四边形

7 总结与展望

可视化证明相较于传统的证明方法能够直观地演示证明过程，降低对证明过程的理解难度［25］。 本文通过对毕达哥拉斯游程问题、巴塞尔问题和托勒密定理为代表的基本数论问题的研究，提出了一种基本数论问题的可视化证明方法，并将这一证明方法应用于托勒密定理的可视化证明中。 所得到的托勒密定理可视化证明结果较为清晰地体现了托勒密定理的证明过程和证明思路，说明这一证明方法具有应用于其他基本数论问题可视化证明的可行性。 除托勒密定理外，毕达哥拉斯游程问题、巴塞尔问题以及Wallis 公式［26］等基本数论问题均能使用这一方法进行可视化证明，从而得到具有易理解特征的可视化证明成果。

可视化教学研究作为未来课堂应用层面的研究，对于教育技术学来讲是一个新的领域，是一个前瞻性的研究，也是一个探索性的研究［27］。一个合适的可视化教学模式和相应的教学策略能很好地把可视化理念应用于教学，并对正在进行的未来课堂的设计与应用实践提供帮助，为面向未来的人才创新思维培养提供学习环境与活动支持［28］。