基于MMO-GIFT 安全性研究*
窦山雀 毛 明 李艳俊
1.北京电子科技学院,北京市 100070
2.中国电子科技集团公司第十五研究所,北京市 100083
引言
随着信息技术的快速发展,移动互联网技术广泛应用于生活的各个方面。 比如:AI 智能机器、无人检测技术、大数据分析和各类智能定位技术。 但是,物联网设备存储、计算、能耗等资源的限制,导致我们需要更为轻便高效的密码算法和协议。 于是,在2018 年NIST 向全球征集轻量级的密码算法,得到了很多优秀的轻量级认证算法,对于这些算法学者提出了一些认证模式。 目前,主流的轻量级密码算法主要有GIFT[1]、PRENSENT[2]、CLEFIA[3]、PRINCE[4]、SPECK[5]、LBOCK[6]、SIMON[5]等。 这些轻量级算法可以通过认证模式构造新的散列函数。 其中GIFT 算法是由Banik 等人2017 年在CHES上提出的一种类似PRESENTF 的新型轻量级分组密码算法。 在CTRSA2019 上,朱[7]等人对GIFT 进行了第一次第三方密码分析,包括对GIFT-64 和GIFT128 分别进行了密钥恢复攻击。Sasaki[8]等人改进了GIFT-64 上的中间相遇攻击(MitM)。 周[9]等列出了GIFT-64 的一些最佳差分特征。
目前,学者对轻量级密码算法的安全性做了大量的分析和研究,而针对散列函数模型的安全性研究并没有受到太多的关注。 直到2020 年,Sasaki[10]等人在EUROCRYPT 针对具体散列函数提出了专用的量子碰撞攻击。 使得散列函数的安全性再次受到关注。 即使压缩函数Ek在经典环境中是安全的,但基于该压缩函数的散列函数仍可能存在碰撞。 因此,深入研究、评估散列函数的安全性是十分有必要的。
1 散列函数
散列函数[11](杂凑函数或Hash 函数)是将任意长度的消息压缩成唯一的、固定长度的散列值,其主要应用在数字签名、数据完整性的检测中。 一个安全的散列算法必须满足抗原像攻击、抗第二原像攻击、抗碰撞攻击这3 条基本的安全属性。 随着现代科学技术的广泛应用,对数字签名、数据完整性的应用需求越来越高,散列函数被应用到各个场景的关键技术中,占有举足轻重的地位。 随着MD5、SHA 算法的破解,评估散列函数的安全性已经变得越来越重要。
散列函数的结构主要有Merkle-Damgard 结构[12]、Tree 结构[13]、Sponge 结构[14]等。 其设计采用了分组迭代,处理过程是将消息格式化处理分组,然后将每块分组消息放入分组迭代中进行处理。 其迭代结构如图1 所示。

图1 散列函数的迭代结构
Merkle-Damgard(MD)结构是经典的散列迭代结构,具有该结构的散列函数对于多碰撞攻击、第二原像攻击、扩展长度攻击有弱抵抗性。针对MD 结构的缺陷,后续也出现了改进的MD结构,主要有随机散列、宽管道结构、HAIFA 结构。 Tree 结构主要用于构造数字签名认证。Sponge 结构主要由初始化、吸收、挤压三部分组成,但是短消息加密效率没有长消息占优势。
目前,现有关于散列函数的分析方法主要有:生日攻击[15]、差分攻击[16]、原像攻击[17]、中间相遇攻击[18]等。 随着量子信息技术越来越多地被用到分组密码等多个密码算法的分析研究。2020 年Sasaki[10]在EUROCRYPT 提出了第一个针对哈希函数的专用量子攻击——反弹攻击,这项工作使得我们的研究不仅仅停留在生日界上,为我们对散列函数抵抗量子攻击的安全性的研究开辟了一个新的视角。
2 GIFT 密码算法
GIFT 算法是基于PRESENT 算法的基本结构而改进的一个算法,GIFT 算法取其“礼物”之意,是2017 年Subhadeep Banik 等人为庆祝PRENSENT 算法发表十周年提出的。 相比于SIMON、SKINNY 算法等轻量级分组密码算法,该算法的算法设计更加简洁、清楚,运行速度快、功耗低。 GIFT 算法采用的是SPN 结构,两个版本分组长度是64 比特和128 比特,都采用128 比特长度密钥,迭代轮数分别是28 轮和40 轮。 关于数据状态的最右侧为最低比特位,形式为bn-1bn-2…b0,n =64 或128。
GIFT 不仅仅是“礼物”之意,其算法设计者也是用打包“礼物”的方式来描述该算法。 该算法的轮函数是由S 盒、P 置换、密钥加组成,把内容放到S 盒里,然后将P 置换作为丝带包裹盒子,最后用密钥加来打结。 关于GIFT-64 的轮函数结构如图2 所示。
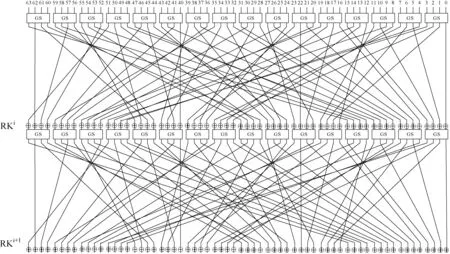
图2 2 轮GIFT-64 算法
S 盒:GIFT-64 和GIFT-128 都是使用相同的4 比特S 盒,该S 盒是非线性部件,结构如表1 所示。

表1 GIFT 算法的S 盒
P 置换:线性层都是采用比特置换,置换表如表2 所示。
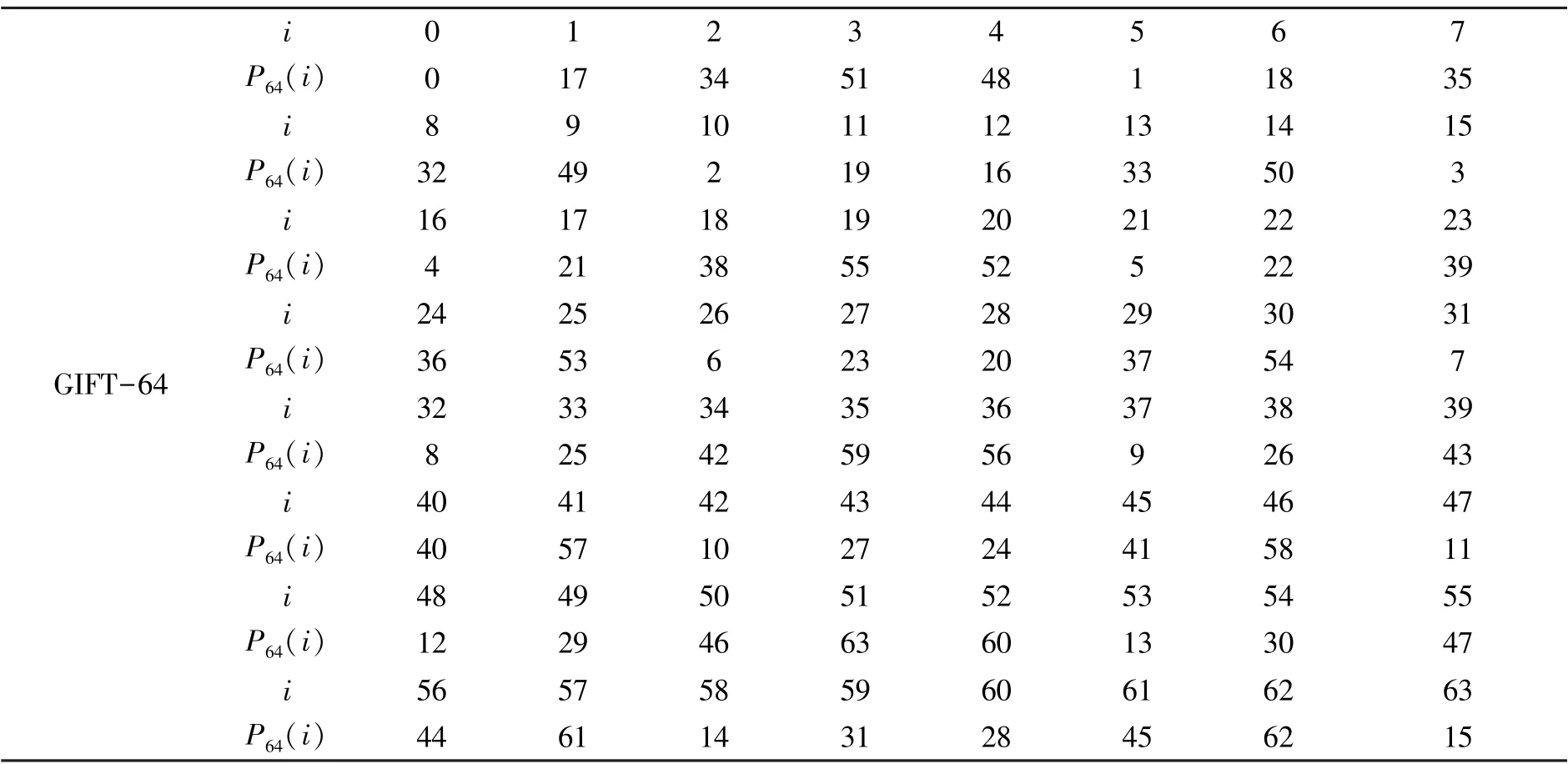
表2 GIFT 算法置换表
密钥加:这部分由轮密钥和轮常数组成,GIFT 算法密钥都是采用128 比特,主密钥通过密钥扩展取32 比特和64 比特的轮密钥RK =U||V,其中U =us-1…u0,V =vs-1...v0,对于GIFT-64,s 为16,GIFT-128 的s 为32。 也就是说,对于GIFT-64 和GIFT-128,每一轮分别有32 比特和64 比特轮密钥参与运算。
对于GIFT-64,U和V分别与b4i+1和b4i相异或。
b4i+1←b4i+1⊕ui,b4i←b4i⊕vi,∀i∈{0,…,15}
对于GIFT-128,U和V分别与b4i+1和b4i相异或。
b4i+2←b4i+2⊕ui,b4i+1←b4i+1⊕vi,∀i∈{0,…,31}
轮密钥均是根据
k7‖k6‖k5‖k4‖k3‖k2‖k1‖k0←k1>>2‖k0>>12‖k7‖k6‖k5‖k4‖k3‖k2
来更新(注意:第一轮的密钥直接提取即可)。 之后我们的数据还需要与轮常数相异或。对于GIFT-n(n =128/256),单独的比特“1”和6比特的轮常数C ={c5,c4,c3,c2,c1,c0} 分别与第n-1,23,19,15,11,7,3 个比特相异或。 轮常数C初始化为0,并按照
(c5,c4,c3,c2,c1,c0)←(c4,c3,c2,c1,c0,c5⊕c4⊕1)
更新每一轮的轮常数。
3 MMO-GIFT 的安全性研究
散列函数的散列模型主要有DM、MMO、MP等,如图3 所示。 通过对MMO 模型的研究,假设密钥输入k固定为初始值iv,Eiv的差分路线概率为p,其输入和输出异或公共值Δ。 给定大约1/p对具有异或值Δ 的输入消息,预计有一对(m,m⊕Δ)遵循这种差异路线:Eiv(m) ⊕Eiv(m⊕Δ)=Δ。 如果密文异或与明文异或相匹配,通过前馈操作后其输出的值为0,即(m⊕Eiv(m)) ⊕(m⊕Eiv(m⊕Δ))=Δ⊕Δ =0。 也就是说,如果输入和输出的有效字节位置以及实际的差异是相同的,就会产生碰撞,MMO 模型的安全性就会大大降低。 因此,对于该模型实例化最低安全轮数的寻找十分重要。
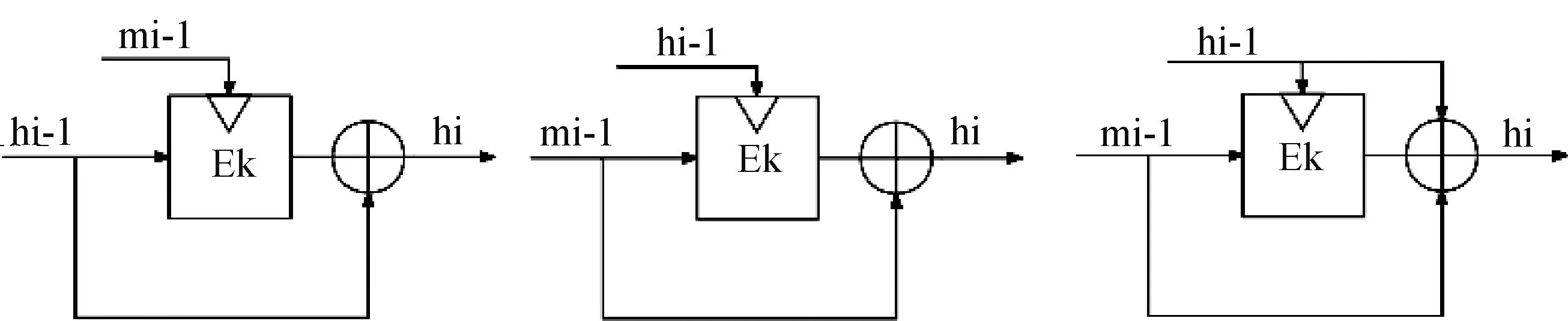
图3 DM、MMO 和MP 散列模型
针对GIFT-64,其空间大小为2-64, 只有找到差分概率高于2-64的差分路线才是有意义的。目前,朱宝玉[19]等人使用MILP 对轻量级分组密码算法GIFT 的差分分析,作者将算法分为外层和内层,针对外层部分,搜索活跃S 盒的数量尽可能少的截断差分路线;算法内层是在外层约束下进一步搜索概率高的差分路线。运用这样的MILP 算法找到多条GIFT 差分路线,对这些差分路线进行分析,发现有一部分12 轮差分路线是由4 轮循环路线迭代而成。在这些12 轮的差分路线中第1 轮输入差分、第5 轮输入差分、第9 轮输入差分和最后一轮输出差分的比特状态是完全一致的,这12 轮的差分路线是由完全相同的三个4 轮循环路线首位链接组成,本文整理了GIFT-64 所有的4 轮循环差分路线,如表3 所示。 这些迭代路线首尾组合之后组成的差分路线包含24 个活跃S盒。 选取迭代路线组成一条12 轮概率为2-60的差分路线。 如表4 所示。

表3 GIFT-64 的4 轮差分迭代路线
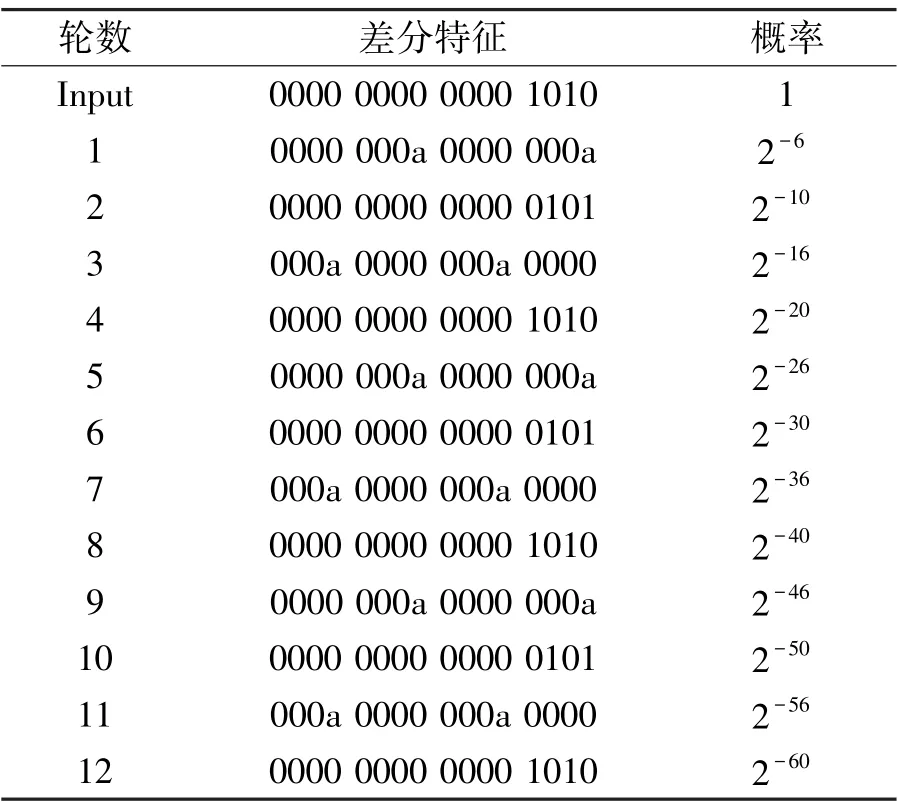
表4 GIFT-64 的12 轮差分路线

轮数差分特征概率4 0000 0050 0000 00502-20 Input0005 0000 0005 00001 1 0000 0000 2020 00002-6 0050 0000 0050 00002-10 3 0000 0000 0000 20202-16 4 0005 0000 0005 00002-20 Input0000 0202 0000 00001 1 0000 0500 0000 05002-4 2 0202 0000 0000 00002-10 3 0000 5000 0000 50002-14 4 0000 0202 0000 00002-20 Input0000 000a 0000 000a1 1 0000 0000 0000 01012-4 2 000a 0000 000a 00002-10 3 0000 0000 0000 10102-14 4 0000 000a 0000 000a2-20 Input0000 00a0 0000 00a01 1 0101 0000 0000 00002-4 2 a000 0000 a000 00002-10 3 0000 0000 1010 00002-14 4 0000 00a0 0000 00a02-20 2
本文主要是对MMO 模型实例化MMO-GIFT的安全性进行分析研究。 根据对GIFT-64 的分析整理,之前对GIFT 算法迭代差分路线的研究都是只有4 轮,其认为寻找轮数更大、概率更高的迭代差分路线也是有意义的,但对于更高轮数并没有进行过多的研究。 本文利用MILP 的搜索算法对GIFT 算法进行了进一步新的搜索、分析,首次提出了一条概率为2-60的6 轮迭代差分路线。 相比于4 轮迭代差分路线,在概率相同的情况下,其迭代轮数更大。 如果将该路线经过两轮迭代,就能够得到一条全新的12 轮差分路线,如表5 所示。 这条路线的提出有利于我们对GIFT 算法的认识以及后续的研究。

表5 GIFT-64 新的6 轮差分迭代路线
通过对GIFT 差分路线的搜索、分析和研究,我们对基于GIFT 新构造的散列函数进行了安全性分析。 通过将GIFT 轮函数作为散列模式MMO 中的压缩函数,构造相应的散列函数。将这样的压缩函数插入迭代结构,这样就可以得到MMO-GIFT 散列。 针对我们之前对散列模型研究发现如果密文差异与明文差异匹配,MMO模式通过前馈操作后输出的差分就会为零,即
(m⊕Eiv(m))⊕(m⊕Eiv(m⊕Δ))=Δ⊕Δ =0
这样的情况其安全性会极大降低。 所以,针对MMO-GIFT 散列函数其轮数大于12 轮的才是安全的。
4 结论
本文主要通过研究散列模型的结构特性,发现如果散列函数中密文异或和明文异或相匹配,那么经过MMO 模式的前馈操作后就会导致输出的结果为零,这样散列函数是不安全的。 为了避免攻击者利用这一性质发起攻击,本文对散列模型的MMO 结构实例化安全性研究,将GIFT算法作为置换函数,构造GIFT 散列,首次提出了6 轮迭代差分路径,在此基础上发现12 轮差分路线的GIFT 散列函数安全性会降低。
通过对GIFT 散列函数的安全性研究,可以知道当我们使用GIFT 作为轮函数的散列函数时,其轮数大于12 轮安全性极大提高。 所以,研究各种分组密码算法作为置换函数的散列函数,为散列函数提供了最小安全轮数。 只要大于这样的最小安全轮数,其构成的散列函数就是安全的。

