三维可压缩Navier-Stokes-Allen-Cahn 方程组Cauchy 问题的适定性

王 静 侯东杰 陈亚洲

(北京化工大学 数理学院, 北京 100029)

引 言

具有扩散界面的非混相两相流模型描述了两种不同流体的流动及流体间扩散界面的运动,其相关研究成果广泛应用于航空航天、水利工程、化学工程等领域。 因此,针对两相流的扩散界面模型进行研究具有重要的理论意义和应用价值。

关于描述单一流体运动的Navier-Stokes 方程的研究已有不少。 相比于单相流,两相流之间存在相互作用和扩散界面,其模型的建立与分析更为复杂。 Van der Waals[1]最先将互不相溶的两相流之间的界面视为一个有厚度的界面层。 之后,Blesgen[2]将描述单一流体流动的Navier-Stokes 方程和描述两种流体在其分界面相互作用的Allen-Cahn 方程耦合在一起,提出了Navier -Stokes -Allen -Cahn(NSAC)方程组。 关于一维NSAC 模型的数学研究结果已有很多,Chen 等[3]证明了初始真空状态下强解和经典解的存在唯一性;Ding 等[4]考虑了NSAC方程组的自由边界问题,证明了强解的存在唯一性;孙颖等[5]证明了NSAC 方程组周期边值问题整体解的存在性;Chen 等[6]证明了非等熵NSAC 方程组初边值问题存在唯一的全局强解;Feireisl 等[7]、Chen等[8]证明了三维可压缩NSAC 模型弱解的存在性。

本文研究三维可压缩Navier -Stokes-Allen-Cahn 方程组的Cauchy 问题。 与前人考虑的初始条件不同,我们假设相场(即组分浓度差φ)在无穷远处趋于1 或-1 两种状态。 因此,除了克服NSAC方程组的强非线性和耦合性,还需要估计φ2-1 所带来的困难项。 针对此类Cauchy 问题,本文在初始小扰动的假设条件下通过能量方法证明了全局强解的存在唯一性。

1 问题的提出及主要定理

可压缩非混相两相流的流动通常由以下的NSAC 非线性偏微分方程组描述

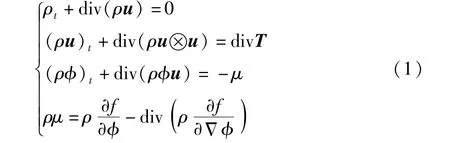
式中,ρ=ρ1+ρ2表示混合流体的总密度;u表示流速,且ρu=ρ1u1+ρ2u2,ρi、ui(i=1,2)分别为第i种组分的密度和流速;φ=φ1-φ2表示组分间的浓度差,其中φi=ρi/ρ;μ表示化学势;f表示界面自由能密度。 Cauchy 应力张量T表示为

本文研究的问题的初始条件为

本文的主要结论如下。

定理1假设初始值(ρ0,u0,φ0)满足条件

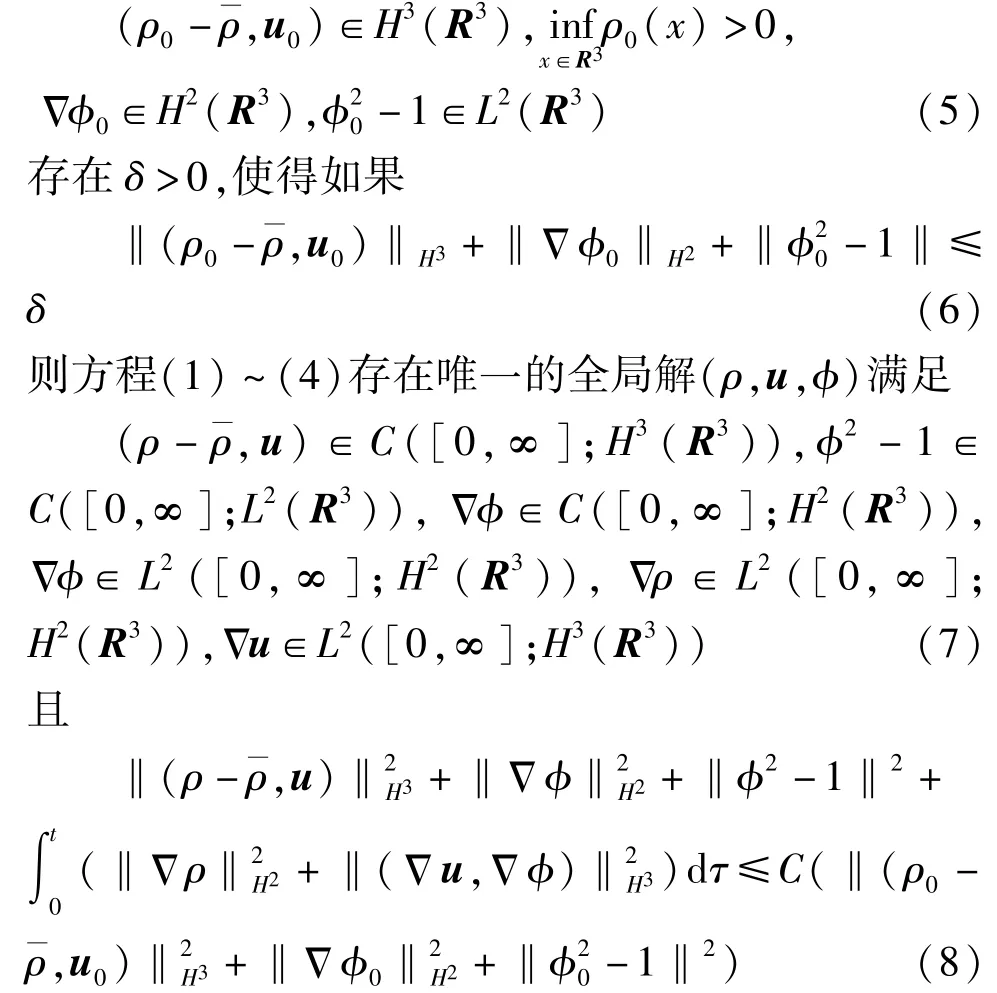
有以下两点需要注意:①式(6)结合Sobolev 嵌入定理,δ足够小时,有,其物理意义为在初始时刻, (两相流出现分层且分层区域 即＜)的测度为零;②记‖·‖=‖·‖L2。

2 主要定理的证明

定理1 中证明全局解的存在性的方法:首先证明局部解的存在性,再利用能量估计的方法得到解的一致估计,最后延拓到全局解的存在性。 在证明过程中,不仅要估计‖(ρ-,u)‖H3+ ‖Δφ‖H2,还要估计‖φ2-1‖。 为克服这些难点,在先验估计中需要假设‖(ρ0-,u0)‖H3+‖Δφ0‖H2和‖-1‖均具有小性。

2.1 局部解的存在性

首先,证明局部解的存在性。

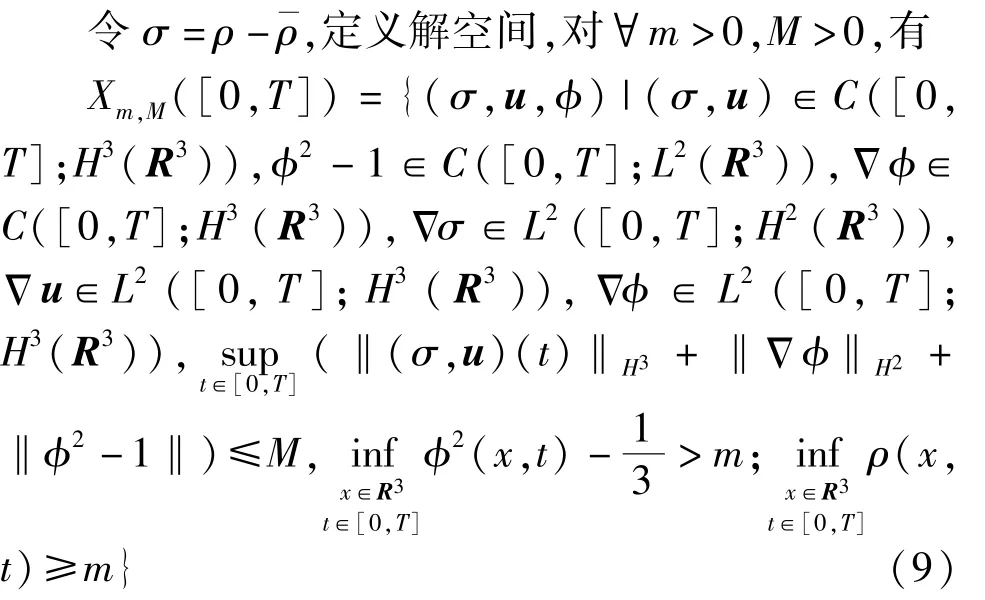
由经典的Schauder 不动点方法得到如下命题。

2.2 全局解的存在性

接着,将方程组(1)写成如下的线性化形式。

其中,非齐次项g1和g2的定义为

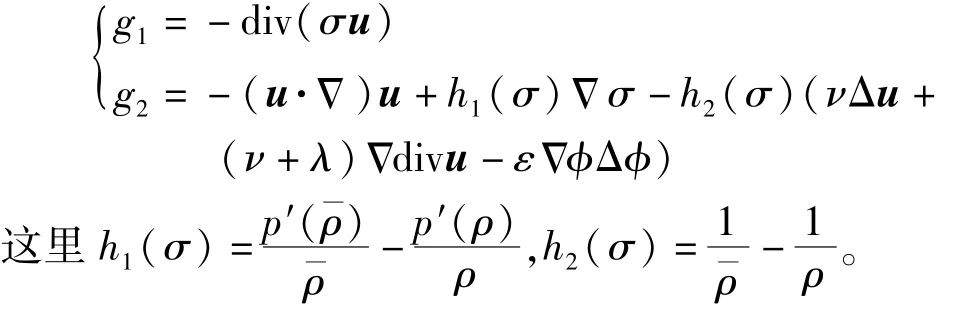
式(10)中第二个式子推导过程中用到

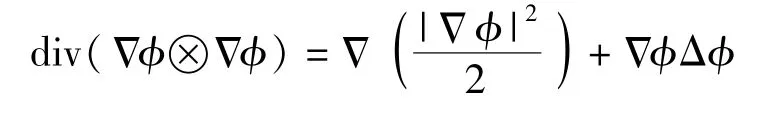
由定义的解空间(9),结合Sobolev 嵌入定理可知,存在M0＞0,使得∀0 ＜M＜M0,有

命题2假设(ρ0,u0,φ0) 满足(σ0,u0) ∈H3(R3),-1∈L2(R3),对∀T＞0,设(σ,u,φ)∈Xm,M([0,T])为方程组(10)的局部解,则存在一个只依赖于初值和T的常数C,使得

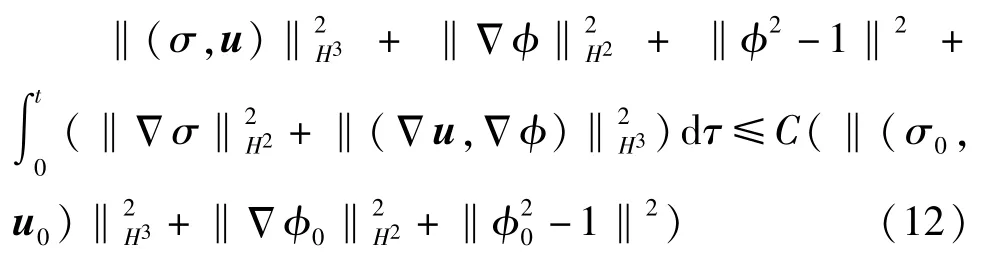
命题2 可由以下4 个引理得到。

引理1设(σ,u,φ)∈Xm,M([0,T])为方程组(10)的局部解,有

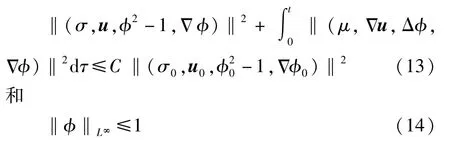
证明:

定义

由式(15)和质量守恒方程得到

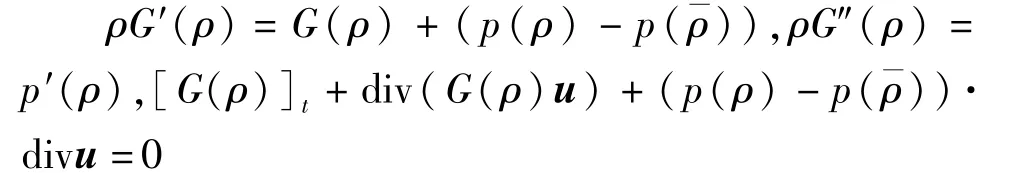
用式(1)中第二个式子乘以u,关于空间变量x积分,有

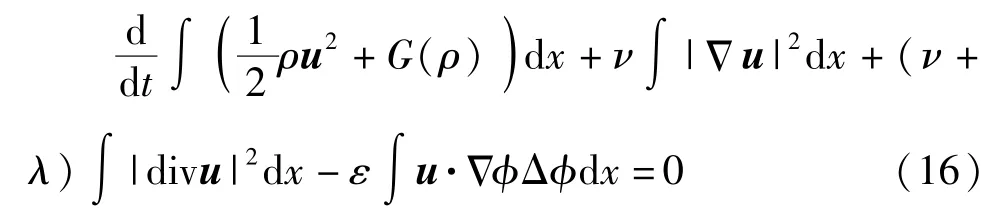
式(10)中第三个式子乘以μ,结合式(10)中第四个式子,关于x积分,利用分部积分得到

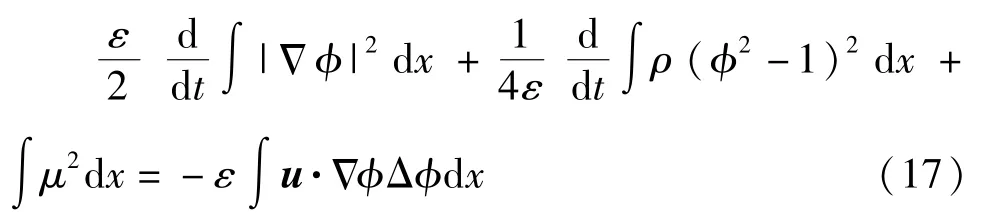
将式(16)和式(17)相加,得到

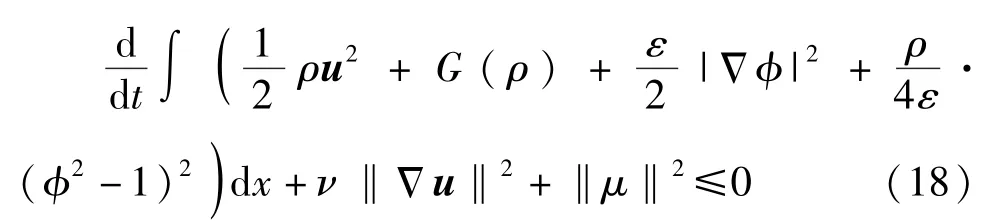
由式(9)、式(11)、式(15)得到

将式(18)在[0,T]上积分,结合式(19)可得

于是有

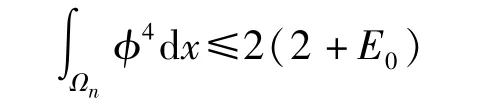
因此可得到

利用式(21)得到

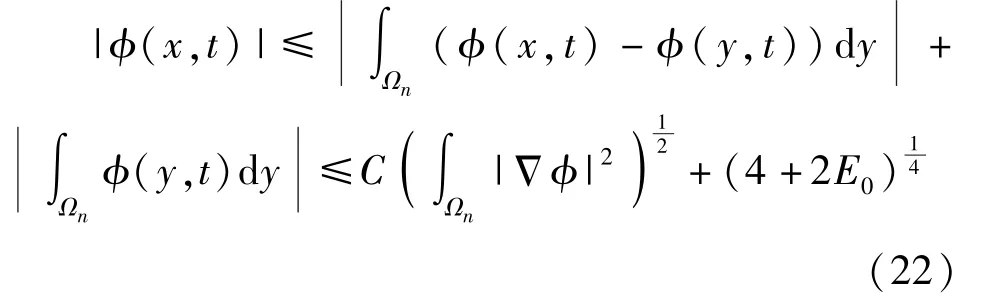
由式(22)和式(20),得到式(14)。

接着,用式(10)中第四个式子乘以-Δφ,再关于x积分,有

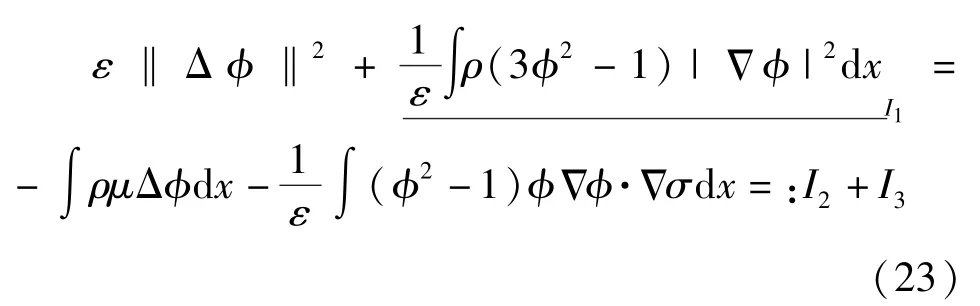
利用式(9)、式(11)和Hölder 不等式得

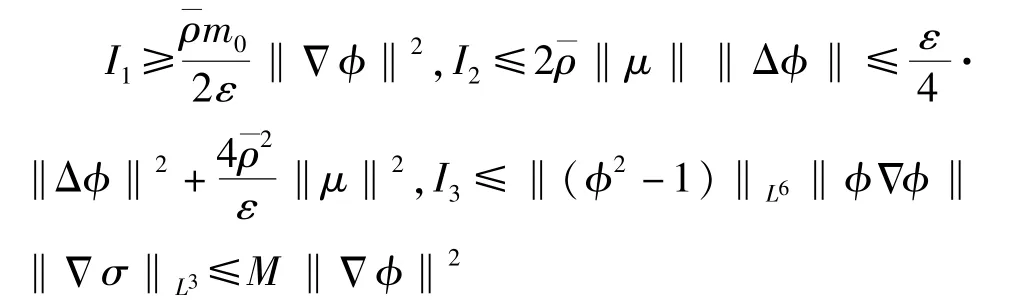
将Ii(i=1,2,3)代入式(23),当M适当小时,有

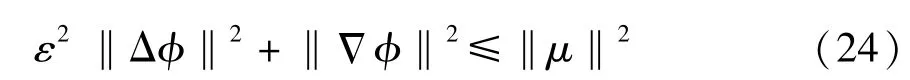
联合式(24)与式(20)得到式(13),引理1得证。

引理2 设(σ,u,φ)∈Xm,M([0,T])为方程组(10)的局部解,有

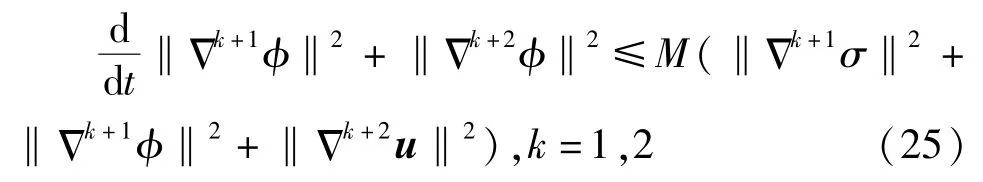
证明:结合式(10)中第三式和第四式,可以得到

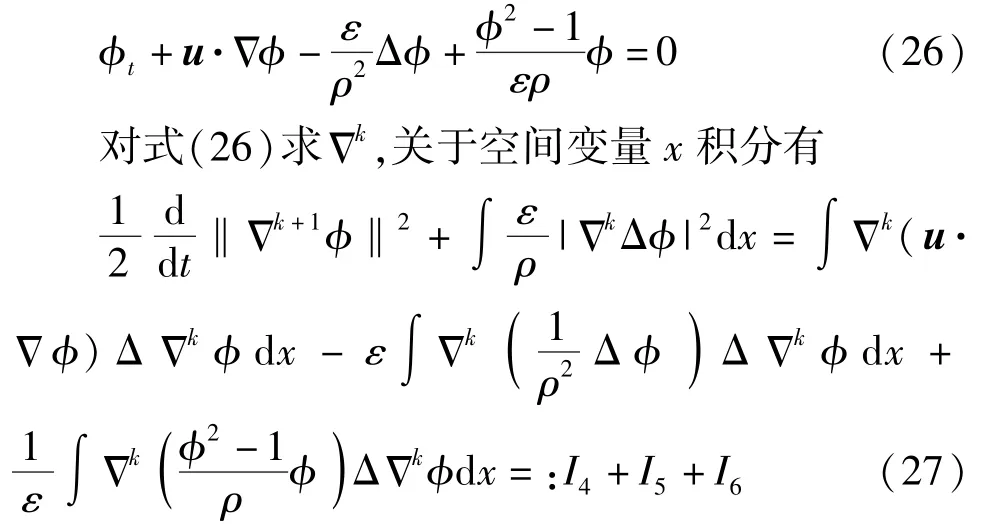
利用莱布尼茨公式、Hölder 不等式和Gagliardo-Nirenberg 不等式,可估计I4为

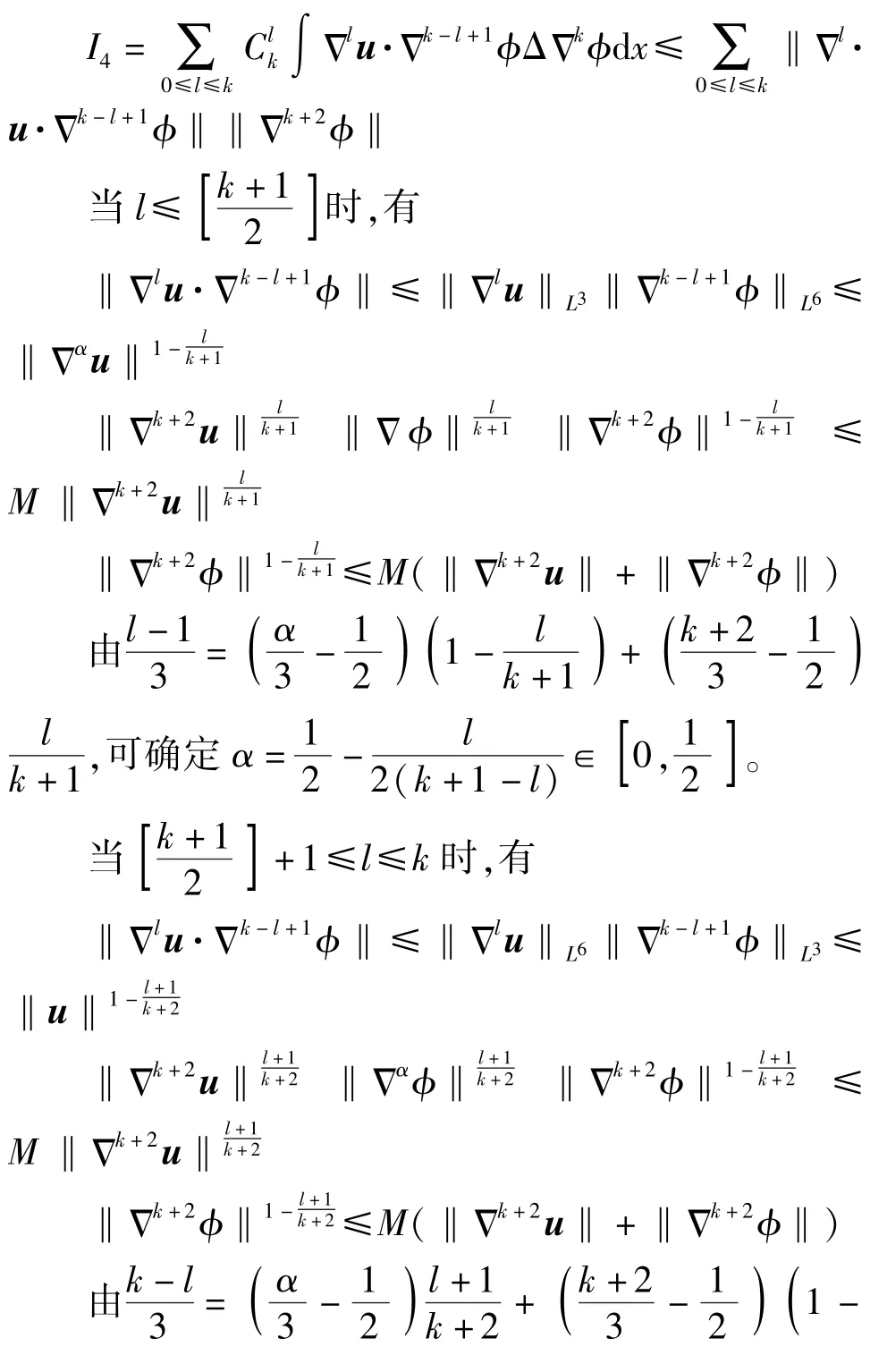
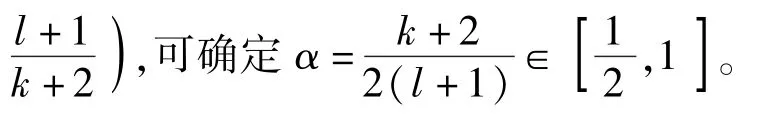
因此,可得到

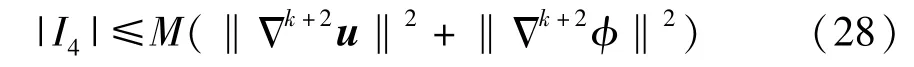
接下来,对I5进行估计。

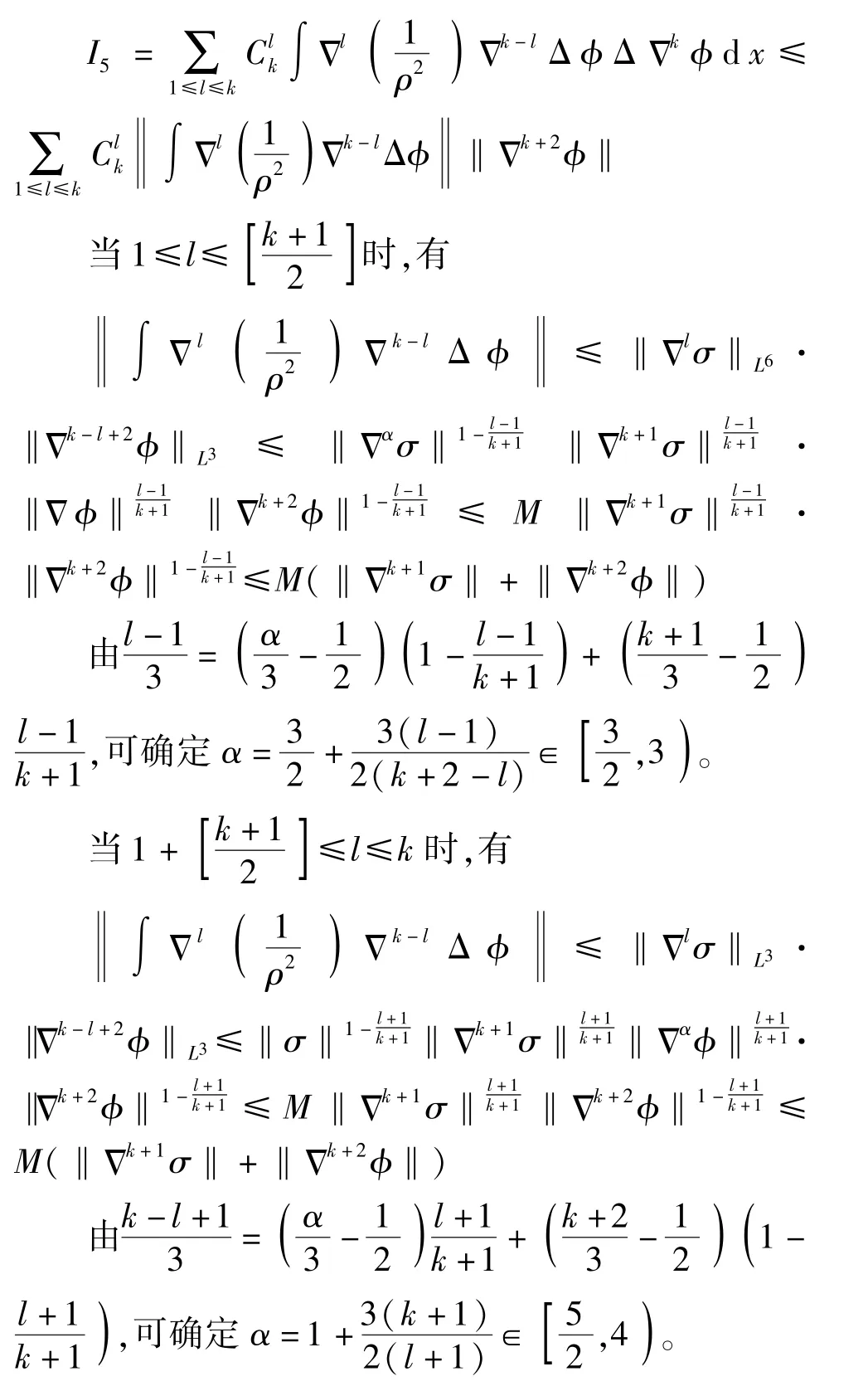
于是得到

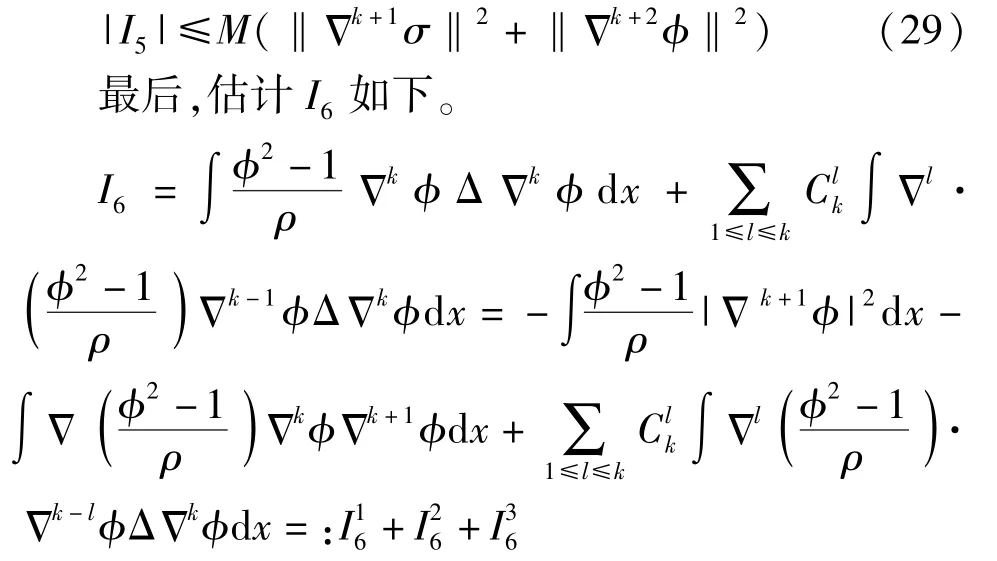
逐项估计可得

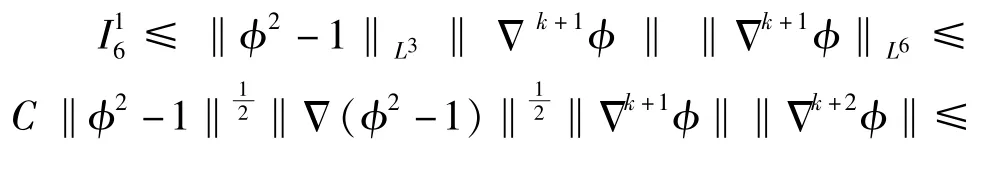
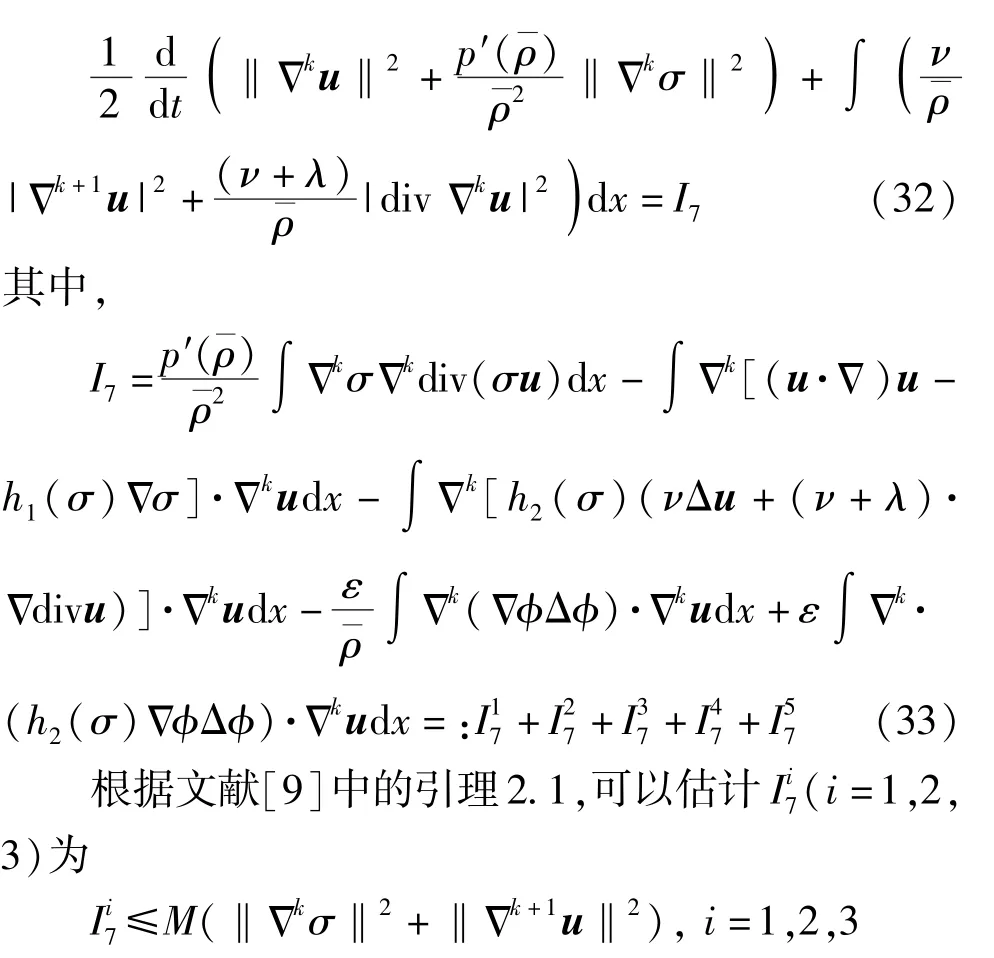
如果k=0, 有

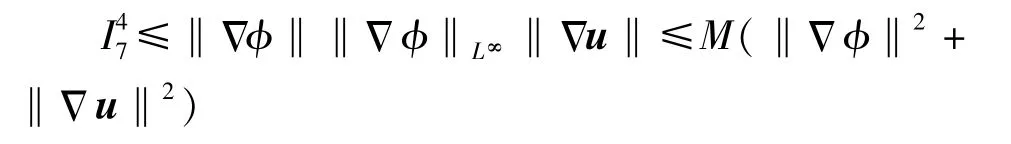
如果k=1,有

如果k≥2,利用莱布尼茨公式、Hölder 不等式和Gagliardo-Nirenberg 不等式,有

引理3设(σ,u,φ)∈Xm,M([0,T])为方程组(10)的局部解,有

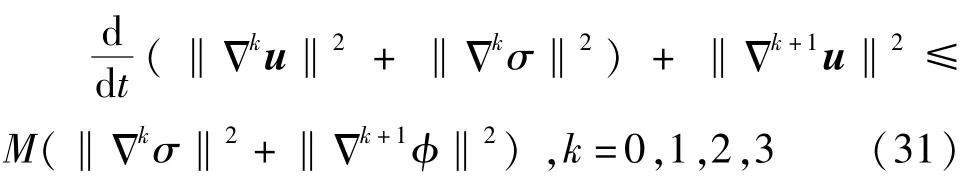
证明:对式(10)中第一个式子和第二个式子求Δk,再乘以Δku,两式相加后,关于空间变量x积分,得

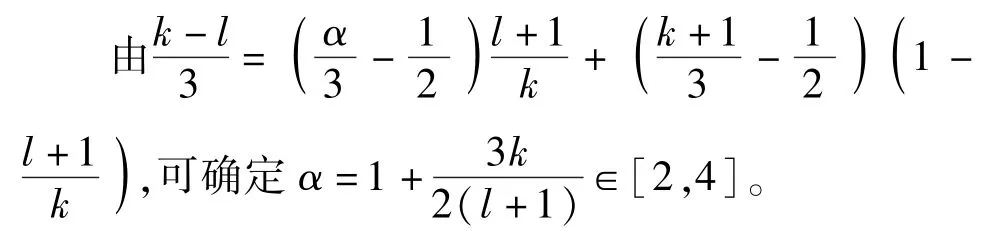
因此,可得到

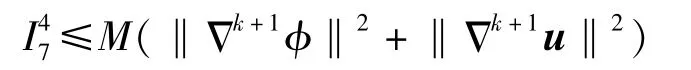
同样可以得到

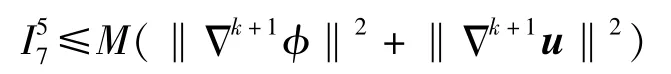
将以上估计代入式(33)有

将式(34)代入式(32),就可以得到式(31),引理3 得证。

引理4设(σ,u,φ)∈Xm,M([0,T])为方程组(10)的局部解,有

根据文献[9]中的引理2.2,可以估计Ii8(i=1,2,3)为

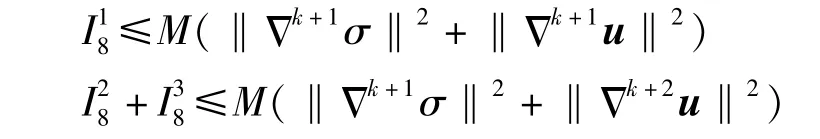
如果k=0,有

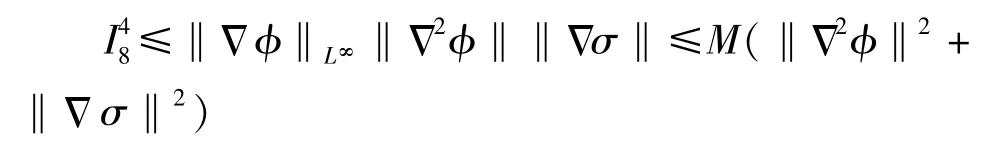
如果k≥1,有

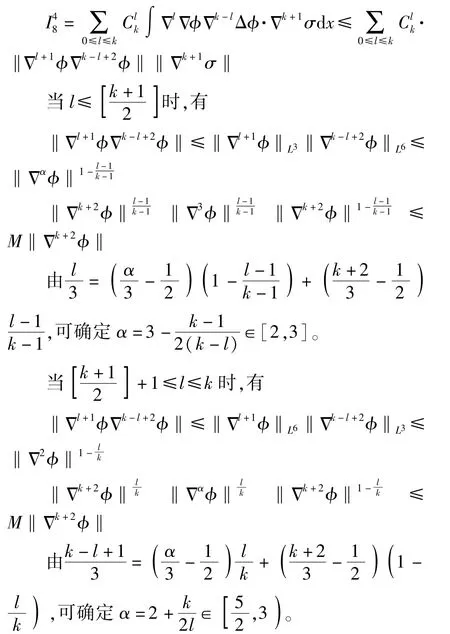
因此,

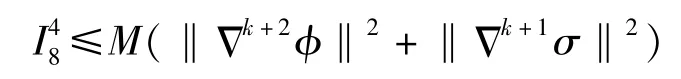
同样可以得到

将以上估计代入式(37),有

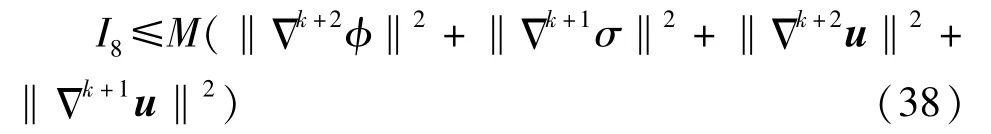
将式(38)代入式(36),得到式(35),引理4 得证。 结合引理1 ～4,命题2 得证,进一步定理1得证。

3 结束语