基于信息粒化和BP-Bagging的股价范围预测模型

赵雅博，何 华

（河北工业大学 理学院，天津 300401）

随着我国市场经济的快速发展和人民生活水平的日益完善，股票投资已逐步成为整个金融业乃至人们生活必不可少的组成部分。若能准确预测股价的波动，合理引导控制股票市场，将进一步推动社会经济的发展，利用股票的历史数据和变化规律，结合科学的方法研究未来股票市场，从而减少企业和个人的风险价值。因此，股票价格预测已成为众多学者的研究方向。

现有研究表明，智能预测模型优于传统模型，尤其是短期预测[1]。神经网络作为一种有效的智能信息处理技术，可根据数据内部之间的联系建模，具有广泛的适应能力，学习能力和映射能力[2-3]，并且三层BP神经网络有合适的隐含层节点数，就能拟合复杂的非线性映射的问题[4]，从而找到非线性的输入和输出之间的联系。基于以上优点，BP神经网络早已被用于股票价格预测的模型当中[5-10]。但是单个BP神经网络在预测股价波动范围时的误差具有一定的随机性，在高维度数据结构下，网络每次的输出结果不一致，甚至会出现较大的差距。为了避免出现这种现象，本文引入了Bagging集成算法[11]，将多个弱预测器组合为强预测器，从而减少过拟合现象，提高预测模型的准确度。目前大多学者主要是对股票价格的点预测进行研究，而股票市场是比较繁琐的，且影响股票的因素众多[12]，因此对股票市场进行精准预测仍然非常困难[13]。在投资理财过程中，对股票价格波动区间预测的研究很有必要，而信息粒化技术具有对大规模数据进行挖掘并根据需要有效提取有用信息的能力，并在以粒子为单位的信息处理中有突出的优势，尤其适用于股票价格波动范围的分析和研究。为此提出了基于模糊信息粒化和BP-Bagging的股价波动范围的预测模型，以股票数据的80%用于训练预测模型，20%用于预测并检验其预测效果，得到未来股票开盘价的波动范围。最后通过预测未来4周的价格波动范围，并与单BP神经网络和SVM的预测结果进行比较，验证了此模型的准确性和应用价值。从预测结果的准确率可以发现，随着时间的推移，预测效果逐渐减弱，但仍可判断股票的涨跌趋势。因此，该模型对短时间内股票开盘价波动范围的预测效果还是具有很大的参考价值。

本文主要是通过时间序列数据预测股票价格，对于其他因素，比如投资者心理情绪、公司突发事件、经济周期的张缩、通货膨胀、国际金融市场的动荡等并未考虑，因此，根据本文预测的效果，同时结合个人、企业和国家的经济波动，理性投资股票，才能减少投资风险，实现最大收益。

1 模糊信息粒化

信息粒化是大数据研究的热点之一，可有效处理大量粗糙信息。最先，Lotfi A.Zadeh（L.A.Zadeh）教授引入信息粒化这一理论[14]，信息粒化就是将整体化为一个个信息粒进行研究。信息粒作为信息的表现形式，通常把一些类似的事物放在一起作为一个集体研究它们的特性，这种处理事物的方法称为信息粒化，所研究的“集体”就是信息粒。对股票价格波动范围的进行预测时，可以根据预测模型的特点将某一时间序列化为信息粒来实验，经过粒化的处理得到各个信息粒的主要信息。

在对高维度数据进行处理时，往往通过建立模糊信息粒反映样本数据的特点，信息粒一般以模糊集的方式体现，用此方法对非线性的时间序列进行模糊粒化，大致可分两个阶段：划分窗口和模糊化。窗口的划分是将股票的数据按时间序列划分为多个小的子序列，每个小子序列作为操作的窗口；模糊化是采用特定的方法对每个窗口模糊化，生成模糊信息粒。窗口划分的长度可以依据原始数据的特点来确定，而模糊化的过程是关键，是在粒化产生的窗口建立模糊集，使其能有效替代原始数据。

本文采用的是Witold Pedrycz的模糊粒化方法，对于单个窗口的问题，把所有的时间序列X看作一个窗口做模糊化处理，模糊化的过程是在X上建立一个模糊粒子P，使其能够合理描述X的模糊概念G，其中G是以X为论域的模糊集合，确定了G也就确定了模糊粒子P：g--ΔxisG,x∈X，因此模糊化过程的核心是确定G的隶属函数A的过程，即A=μG。通常情况下模糊粒子的形式有三角形、梯形、高斯形、抛物形，由于三角形模糊粒子简单易行，根据本文数据量的大小，采用三角形，其隶属函数为：

式中：x是论域中的变量；a、m和b是参数。a、m和b分别对应于各个窗口模糊粒化后生成的3个值：Low、R、Up。在每个模糊粒子中，Low体现了股票初始样本波动的最小值，R体现了股票初始样本波动的大体平均水平，Up体现了股票初始样本波动的最大值。模糊信息粒化主要是通过整体当中各个部分之间的协作和信息共享来实现误差最小，其特点是降低维数，收敛速度快，容易实现BP神经网络对训练样本的拟合。

2 BP-Bagging模型

2.1 BP神经网络模型

BP神经网络是一种信号前向传递、误差反向传播的多层前馈神经网络。对于时间序列预测模型来说，其实质是构造一个非线性的函数f(x)去逼近F(x)的方法，即F(xi)=f(xi+T) ,T＞0，其中T为预测的时间长度，而BP神经网络就能很好的构造出一种非线性的预测模型，网络的输入和输出分别代表该函数的自变量和因变量。

BP神经网络是由输入层、隐含层、输出层组成的，通常需要进行两个阶段的数据处理。首先是由神经网络隐含层的激励函数对输入数据进行非线性的变换，其次网络的输出由函数响应值通过输出层的组合加权得到。根据输入输出序列(X,Y)确定输入层节点数N、隐含层节点数L、输出层节点数M，这样BP神经网络就实现映射f:Rn→Rm。由输入向量X，计算隐含层的输出

式中：ωij为输入层与隐含层的连接权重；aj为隐含层的初始阈值；f为激励函数。同理可得网络的预测输出

式中：ωjk为隐含层与输出层的连接权值；bk为输出层的初始阈值。进而可计算网络的预测误差：ek=gk-Yk，其中预测误差可在网络训练前提前设定参数值，在未达到误差参数值情况下，根据BP神经网络误差反向传播原理，需要不断地更新连接权值ωij和ωjk：

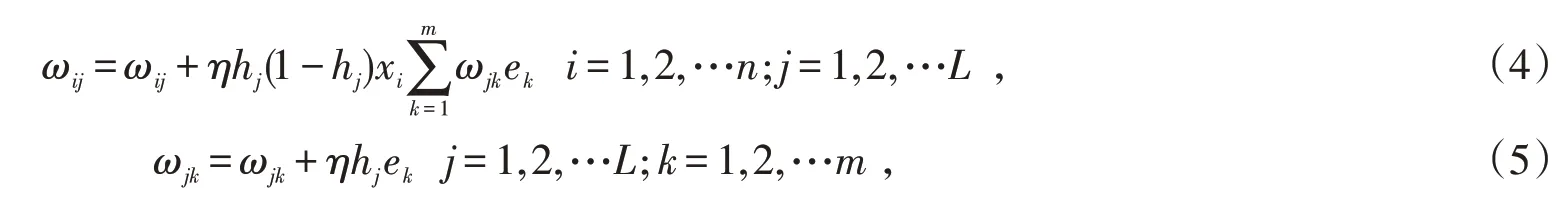
式中，η为训练时的学习速率。同时更新网络节点的阈值aj和bk：

这样BP神经网络在学习过程中，通过网络输出得到的误差不断更新网络连接的权值和阈值，样本数据中所隐含的规律逐渐刻画到网络中，从而得到符合此规律的BP神经网络预测模型，使得网络的预测值和真实值达到一致。

从上述算法中可以看出，随着训练数据规模的增大，神经网络的学习效率随之下降，泛化能力受到限制，通过模糊信息粒化的方法可以对训练样本进行划分，生成多个粒，并将该结果作为训练样本。直观上就可降低样本数据的规模，节省时间复杂度。

2.2 Bagging算法

Bagging算法是应用最为广泛的集成学习算法之一，基本思想是将多个不同的弱学习器通过等权平均的方法组成强预测器，以提高预测模型的准确性。其特点是可并行计算，降低弱学习算法的不稳定性，从而改善整个预测模型的泛化能力。

Bagging集成的过程是给定一个弱学习器和一个训练集{(x1,y1),(x2,y2),…,(xn,yn)}，每次从训练集中随机选取m(m＜n)个训练样本，训练结束后生成预测模型fi，再将训练样本放回初始训练集中进行下一次的选取，保证每次所取的训练样本容量相同，这里初始训练集中的样本在经过多次抽取过程后有可能是不存在的。k次训练以后可以得到一个预测模型序列：f1,f2,…,fk，最终强预测模型的结果采用算术平均的方法得到模型的输出。BP-Bagging预测模型的流程如图1所示。

图1 BP-Bagging算法流程图Fig 1 BP-Bagging algorithm flow chart

3 基于模糊信息粒化的BP-Bagging模型

股票开盘价具有很强的波动性和不确定性，对于股票开盘价的预测不能只局限于点预测的分析，还要进行一段时期内股票价格波动范围预测的研究。信息粒化是在数据挖掘中对大量复杂信息进行模糊处理的有效工具，可反应数据的模糊属性。此外，BP神经网络在处理非线性问题方面具有较好的拟合能力，但在训练过程中会出现过拟合的现象，泛化能力有所减弱，网络每次的输出结果不稳定。Bagging是一种提高预测能力的集成学习算法，可对弱预测器并行拟合，适用于“不稳定”的预测方法，从而提高预测模型的准确性。考虑到单一模型的局限性，难以改善模型的预测能力，本文将BP神经网络和Bagging算法相结合，构建BP-Bagging模型，利用不同算法的优点，形成强预测器。

经过信息粒化对原始数据的预处理，可以得到原始数据的模糊粒，降低样本规模，减少时间的复杂度。然后将模糊信息粒化后的训练数据进行随机有放回的抽取，保证每次所得子样本容量相同，得到若干个子训练集，用于训练不同的BP神经网络模型，最后由Bagging组合的方法输出最终的预测结果，以提高学习速率，增强泛化能力，避免出现过学习的现象，从而保证预测结果的准确性。为此提出了基于模糊信息粒化和BP-Bagging的股价波动范围的预测模型，具体步骤如下。

1）提取初始训练数据集，并确定模糊粒化窗口的长度。

2）采用三角形模糊粒子对样本数据进行处理，分别得到粒化后的Low、R和Up的范围值，并进一步做归一化处理：

式中：xmin=min(x)；xmax=max(x)。

3）从初始训练集中随机有放回的抽取相同容量的k个子训练集。

4）生成的训练子集用于训练单BP神经网络，得到k个不同的弱预测模型，分别输出各个窗口的Low、R和Up值。在神经网络结构中，隐含层和输出层的传递函数分别为tansig和purelin，最大迭代次数设置为10 000，错误目标精度设置为10-6，初始权重随机产生。在训练过程中，达到最大迭代次数或者错误目标精度即终止，输出预测结果。

5）反归一化，并对k个弱预测输出采用Bagging集成算法确定最终的强预测结果。

6）对区间预测的结果进行对比，验证组合预测模型的精确性和有效性。

4 实例分析

本文通过网易财经选取中信证券（600030）股票2007.11.17—2017.11.17日期内2 405组数据的开盘价进行分析，以前1 885 d的数据作为神经网络的训练集建立预测模型，1 886～2 385 d的数据作为预测，由于本文主要研究股价波动范围的短期预测，故把最后20 d数据作为验证集，以说明模型预测的有效性。

首先以5个交易日为模糊窗口，采用三角形隶属函数对样本数据进行模糊信息粒化，得到各个窗口的最小值、大体平均水平和最大值，结果如图2所示。

图2 开盘价模糊信息粒化后的结果Fig.2 Result of granulation of open price fuzzy information

利用此模型分别对Low、R和Up值进行回归预测时，3个值的预测过程相似，这里仅以R值的预测结果为例，将R进行归一化处理，结果如图3。

图3 粒化后的R值归一化的图像Fig.3 Grained R-valued normalized image

从1 885 d的训练数据（377组R值）中，随机选取1 500 d的数据（300组R值）作为样本训练集，有放回的选取k次后分别用于训练单BP神经网络，得到k个不同的预测模型，对k个预测模型的回归结果求等权平均得到的值即为最终的模型输出，并画出单BP网络、BP-Bagging的预测值和真实值得对比图，如图4所示。

图4 R的预测值与真实值的比较Fig.4 The Compare of R′s Predicted Values to Real Values

为进一步验证预测模型的稳定性和准确性，本文采用区间准确率的指标进行评价：设A为实际波动范围，B为预测波动范围，则区间准确率100%。结合BP-Bagging模型和单BP神经网络模型得到测试集的股票预测价格波动范围和实际波动范围的对比表，如表1、表2所示。并采用喻胜华[15]提出的支持向量机的方法同样进行预测，得出的结果如表3所示。

表1 BP-Bagging预测开盘价的变化范围和准确率Tab.1 BP-Bagging predicts the range and accuracy of the opening price

表2 BP预测开盘价的变化范围和准确率Tab.2 BP predicts the range and accuracy of the opening price

表3 SVM预测开盘价的变化范围和准确率Tab.3 SVM predicts the range and accuracy of the opening price

通过对比可以发现，本文所建立的BP-Bagging模型预测结果的准确率相对于单BP神经网络和SVM是较高的，这也充分说明了Bagging算法对于不稳定的预测器有一定的改善。随着时间的推移，不确定因素的增加，预测的精度有所下降，但根据区间的变化也可判断出在这段时间内，中信证券股票的开盘价先跌后涨，与实际情况的波动趋势相同，这也为投资者提供了有利的理财依据。

5 结论

本文首先利用模糊信息粒化方法对原始数据进行处理，分别得到粒化后的最小值、大体平均水平和最大值，其次利用随机采样方法获取不同的训练数据集，分别训练多个BP神经网络，并结合Bagging算法将多个模型进行集成得到最终的预测输出，构建了以开盘价波动范围为输出量的强预测模型，最后通过BPBagging、单BP神经网络和SVM预测结果的对比，进一步验证了此模型对未来短时间内股票价格预测的有效性和准确性。虽然可以实现对未来股票开盘价的涨跌范围进行大致预测，但无法实现精准预测，主要是因为股票价格受到市场不确定因素、国家经济政策和投资者的风险承担能力等的影响。因此，在实际的操盘中，投资者可根据预测得到的股票开盘价的变化范围，留出更多的考虑时间，结合当前企业的经济状况，以实现最大收益。