电压暂降分类算法及应用分析

刘亚丽，于光耀，李国栋，汪颖，禹华西

（1.国网天津市电力公司电力科学研究院，天津 300384；2.四川大学电气工程学院，成都 610065）

0 引言

电压暂降事件是电力系统中不可避免的电能质量问题，其对工业过程的影响和造成的重大经济损失，受到了工业界和学术界的广泛关注[1-4]。电压暂降类型是暂降事件的重要特征，为电网侧故障类型识别、用户侧敏感设备耐受能力测试及电压暂降治理方案的制定等提供决策信息。

电压暂降治理可分为电网侧治理和设备侧治理两大类。电压暂降类型是进行治理方案决策的关键因素之一。在电网侧，电压暂降类型能够反映相关故障信息[5]，例如A 类暂降是由三相短路故障引起，相间短路会引起C 类暂降等。同时，电压暂降经变压器传播可能会导致幅值和相位变化，造成暂降类型的变化[6-7]。基于电压暂降经变压器的传播机理和监测到的暂降类型，可分析出相应故障类型，为电网侧治理决策提供依据。

在设备侧，采用动态电压恢复器、不间断电源等补偿措施进行电压暂降治理[8-10]，是工业界的主流治理方案，暂降类型信息是确定补偿容量的重要参考。比如，当接入点的大多数暂降是B 类或者D 类时，说明有两相电压未发生明显跌落，补偿容量可考虑按被补偿设备容量的三分之一或更小来进行设计。相应地，电压暂降类型是进行敏感设备耐受能力测试时不可或缺的因素。IEC 61000-4-11[11]、IEEE 1668—2017[12]及CIGRE C4.110 报告[13]等都建议，进行敏感设备的电压暂降耐受能力测试时，应考虑不同暂降类型对设备耐受能力的影响。在国内，华北电力大学等单位进行的变频器测试，证明了暂降类型对设备耐受能力有重大影响[14-15]，2019年底审核通过的电力行业标准《低压变频器电压暂降及短时中断穿越能力测试技术规范》中，也特别对测试暂降的类型进行了规定，相关国标也正在同步拟定。

目前，国外学者提出了一些以C 和D 类型作为分类目标的电压暂降分类算法[16]。本文详细分析了5 种典型电压暂降分类算法，应用大量仿真数据和实测数据验证典型算法。同时，对比不同算法的计算结果，分析导致算法不适用的主要原因，并提出算法改进建议。

1 典型算法概述

本文主要研究了5 种典型的暂降分类算法，包括对称分量法（symmetrical component algorithm，SCA）[16]、六相法（six-phase algorithm，SPA）[16]、TP-TA法（three phase three-angle algorithm，TP-TA）[17]、空间向量法（space vector algorithm，SVA）[18]和TPA 法（three-phase-angle algorithm，TPA）[19]。

1.1 SCA法

SCA 法根据正序电压V1和负序电压V2的关系计算电压暂降类型，如式（1）所示。

为解决相位跳变过大造成误判的问题，提出了修正后的计算公式，见式（2）。T为四舍五入后的整数，其值与暂降类型的关系为

1.2 SPA法

SPA 法根据不包含零序电压的6 个线电压和相电压中的最小幅值计算暂降类型。该方法对相位跳变比较敏感。由于已有学者比较了对SCA 法和SPA 法的应用效果[20]，本文不再进行对比。

1.3 TP-TA法

TP-TA 根据3 个电压幅值和相角，计算暂降类型，该方法基于损失电压RV计算电压损失率IRV，两个参数的表达式如式（3）。

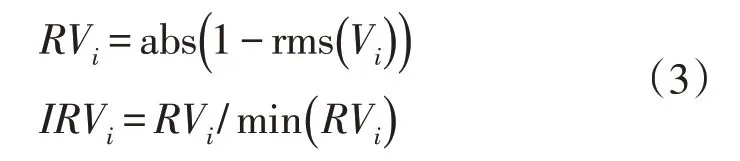
式中，i=a、b、c，为电压相数。

损失电压是表征暂降幅值的参数。电压损失率差值ΔIRV定义为

IRVmax1和IRVmax2是3 个电压损失率中降序排列的前两个值。其次，文献[17]将3 个相角定义为

最后根据以上参数，计算暂降类型，方法如下：

1）RVmin=0→C 类暂降，暂降对称相与最小损失电压RV所在相对应。

2）ΔIRV＜3 且与RVmin所在相相对的其他两相之间的相角小于120°→C 类暂降，暂降对称相与最小损失电压RV所在相对应。

3）ΔIRV≥3 且与RVmax所在相相对的其他两相之间的相角大于120°→D 类暂降，暂降对称相与最大损失电压RV所在相对应。

1.4 TPA法

TPA 法基于电压不平衡参数CVUF和β角计算暂降类型。参数CVUF定义为

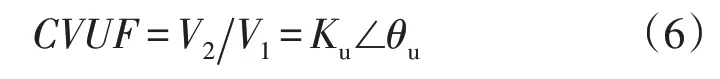
其中Ku和θu分别为电压不平衡参数的幅值和相位。β角表示为

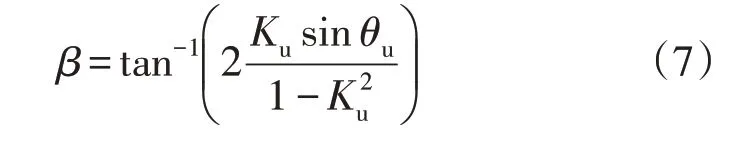
三相电压Va、Vb和Vc的相位分别为φa、φb和φc，线电压Va-Vb，Vb-Vc和Vc-Va的相位分别为φab、φbc和φca。TPA 根据12 个相角φa±β，φb±β，φc±β，φab±β，φbc±β和φca±β中的最小值（绝对值）计算暂降类型。暂降类型与最小相角绝对值对应关系为

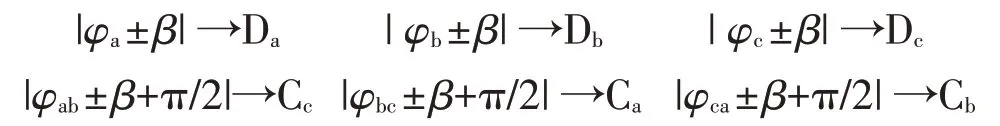
1.5 SVA法

SVA 法将电压波形作为输入，计算暂降类型。三相电压瞬时值构成空间向量x（t）为

其中α=ej2π/3，该空间向量可以描述为向量的正序分量和负序分量的和，如式（9）。

电压暂降期间，波形的空间矢量在复平面上的轨迹接近圆（平衡暂降）或椭圆（不平衡暂降），SVA 法根据椭圆较长半径的倾斜角度确定暂降类型，判据如下：

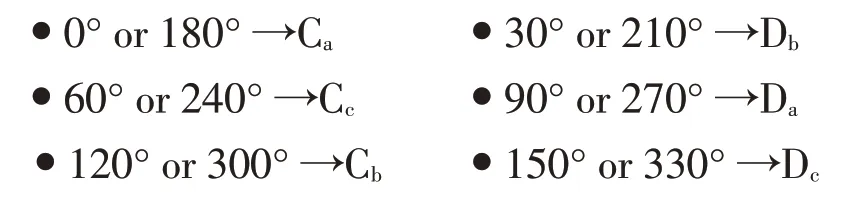
2 数据来源

文献[16-19]并未采用大量仿真数据和实测数据，验证上述5 种算法。为分析相关方法的适用性，本文分别应用21 组仿真数据、合成仿真数据和216 组实测数据，分析比较了5 种算法的计算效果。为了方便描述，将21 组仿真数据和合成仿真数据分别命名为仿真数据1 和仿真数据2。

2.1 仿真数据1

仿真数据1 来源于文献[16-19]，是上述5 种算法提出时，分别用以验证各种算法的仿真数据。共21 组数据，见表1，数据编号后的括号内是该暂降数据对应的类型。需要说明的是，其中编号为3，4，7，8，11，12，15，16 的电压暂降，相位跳变较大，这种情况几乎不会在电力系统中出现。

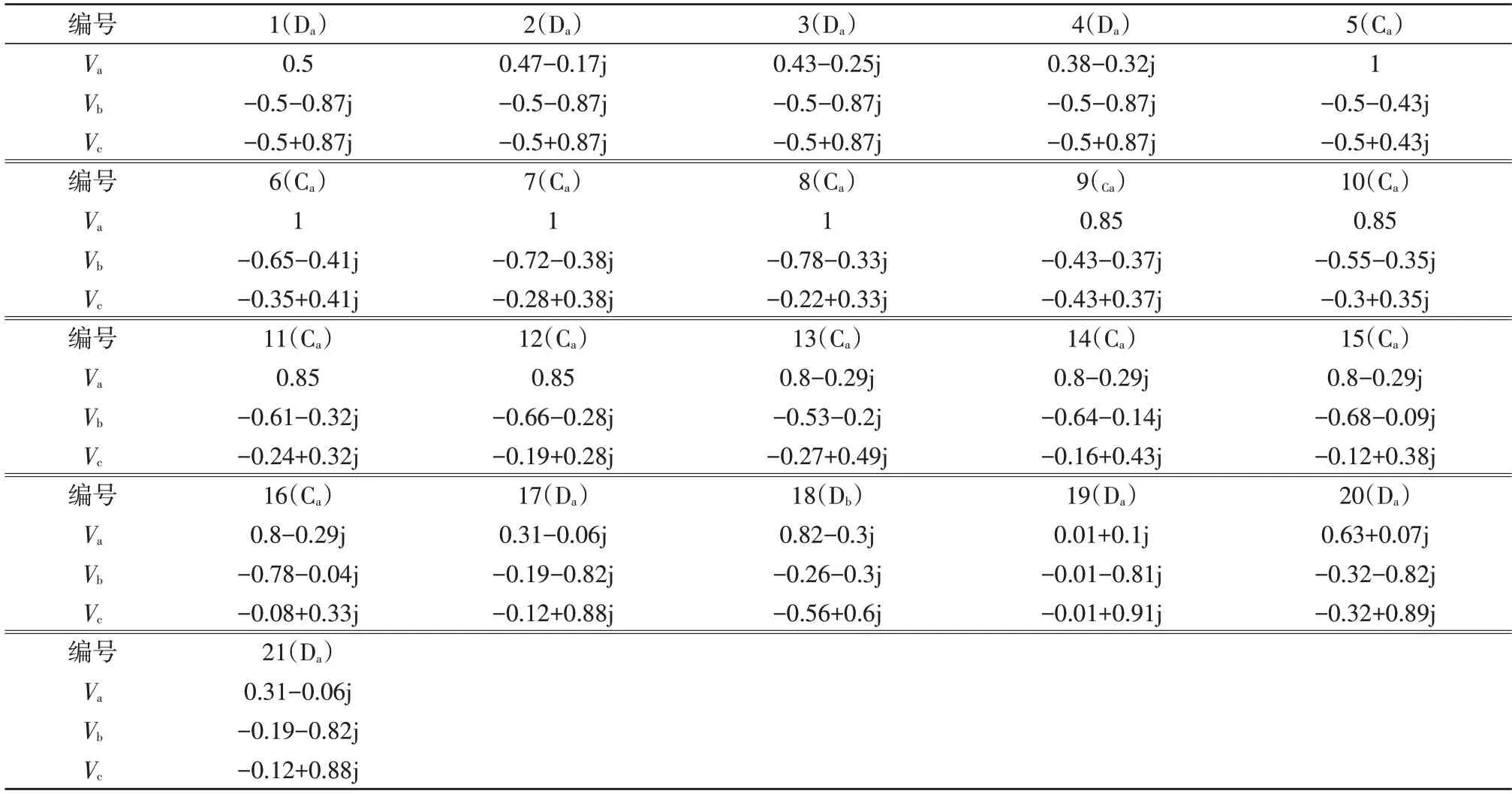
表1 电压暂降仿真数据1Table 1 Voltage sag simulation data 1

2.2 仿真数据2

仿真数据2 根据电压暂降类型定义公式构建[16]。该公式中，确定暂降类型的重要参数是特征电压CV，本文考虑CV的幅值和相位，构建了10 000组电压暂降，包含了所有可能发生在电力系统中的暂降情况。特征电压幅值样本数为100，范围为0～0.99p.u.；相位样本数为100，范围为-90°～90°，最终合成10 000 组仿真数据用于算法验证。

在实际电力系统中，并非所有合成暂降均会发生。根据文献[20]，当系统X/R为10，馈线X/R为0.5 时，阻抗角为可能的最大负值，大约为-60°；如果系统与馈线的X/R几乎相等，此时阻抗角有最小正值，大约为10°。因此，实际阻抗角几乎都在-60°到+10°之间，在10 000 组合成电压暂降中，大约只有3 800 组能在实际电力系统中被监测到。

2.3 实测数据

本文采用216 组河南电网实测电压暂降波形，提取每相电压幅值和相位，获得三相电压矢量作为分析对象。

3 SCA法&SPA法

计算仿真数据1 的类型时，SCA 法的计算结果均正确；而应用SPA 法计算暂降类型时有8 组错误结果，分别将第3、4、7、8、11、12、15、16 的结果判断为了Cc、Cc、Dc、Dc、Dc、Dc、Dc、Dc。对于构建的10 000 组电压暂降仿真数据，本文的计算结果表明SCA/SPA 法能够准确计算出78%/62%的暂降类型，Math Bollen 在文献[16]和文献[21]中已对SCA 法和SPA 法进行了详细的应用效果分析，本文不再赘述。

在构建仿真数据时，电压暂降的类型是已知量；但是，对于监测得到的实际电压暂降波形，暂降类型是未知量，所以进行分析研究时，很难直接使用准确率指标来描述某种算法的性能，本文主要采用方法结果相似程度对比和部分案例人工判断（假设人工判断结果为准确结果）来分析各算法的性能。应用SCA 和SPA 计算216 组实测暂降数据类型，结果相同的数量为135 组。对于相位跳变较大或暂降深度较浅的暂降，SPA 法非常敏感，导致结果错误；针对上述两项影响因素，SCA 的计算结果比SPA 有明显的提升，但是仍对大相位跳变和浅暂降的情况敏感。

4 TP-TA法

应用TP-TA 法计算仿真数据1 的类型，结果均正确。仿真数据2 根据Da和Ca类型的表达式合成，基于仿真数据2 的TP-TA 法测试结果见图1。正负序因子F为1 时，Da类型的测试结果如图1（a）所示，图中所示平面的横坐标为CV的幅值，纵坐标为相位跳变，平面上的每一个点表示一次电压暂降，共计10 000 个点。图中黑色点集表示错误的计算结果；实线表示电力系统中实际暂降的边界，两条实线内的区域为实际电力系统中电压暂降的幅值和相位跳变区域。

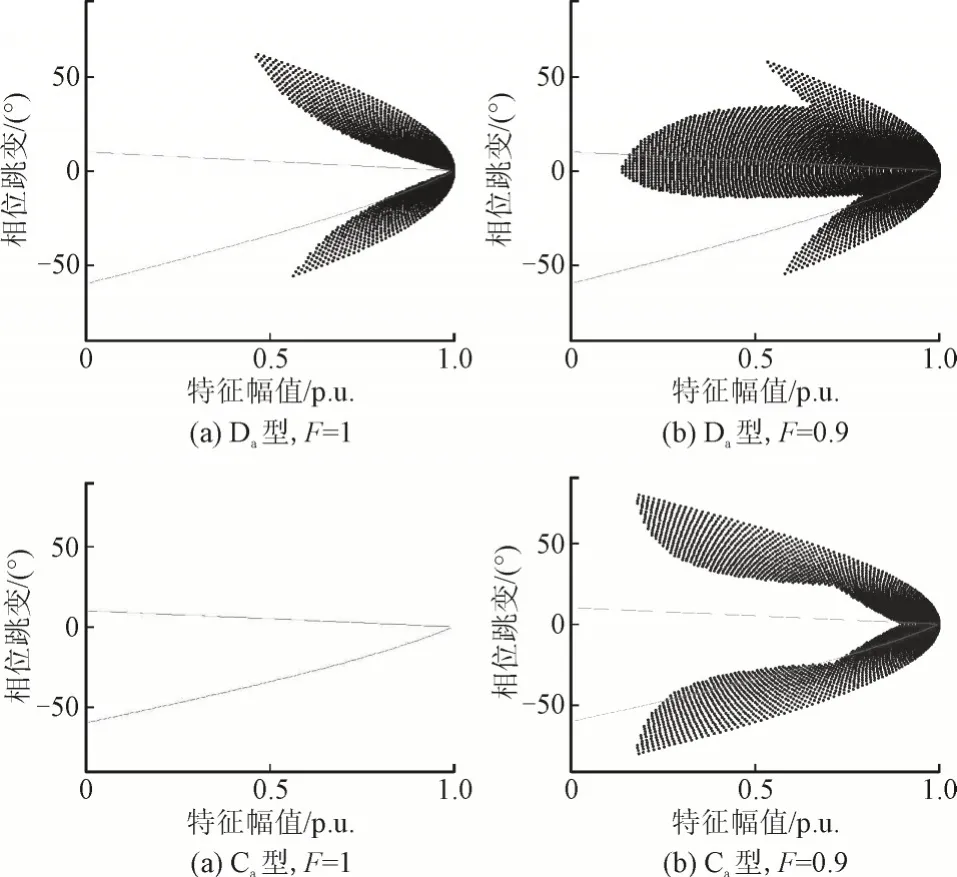
图1 TP-TA法验证结果Fig.1 Verification results of TP-TA

由图1（a）可知，对于相位跳变过大的合成仿真数据，TP-TA 法会发生误判。根据图1（b），当F为0.9 时，TP-TA 法对于许多相位跳变较小的暂降事件也会造成误判。根据图1（c），对于Ca类合成数据，当F为1 时，结果都正确。而当F为0.9 时，TP-TA 法会误判相位跳变过大的暂降，如图1（d）。应用仿真数据2 进行验证时还发现，TP-TA 法的类型判据没有能覆盖所有电压暂降情况，经计算，10 000 组Da/Ca类型的数据中，有500/500 组不符合TP-TA 的各条判据，无法得到类型计算结果，图1（a）-图1（d）中的黑色点集中还包含了一部分结果未知的数据。

应用TP-TA 法计算216 组实测暂降的类型，有86 组数据未能得出结果，见表2。以表2 中的3 组案例为例（案例22，23，24）进行说明。这3 组电压向量图见图2，3 个ΔIRV值均小于3，但与RVmin所在相相对的两相之间的相角大于120°。在案例22中，RV最小值为RVb（RVb=0.08），与RVb（φca）所在相相对的两相之间的相角为123.86°，超过了120°，根据1.3 描述的算法判据，不能得出结果。

表2 应用TP-TA法未能得出结果的3组案例Table 2 Three groups of cases with result not obtained by TP-TA

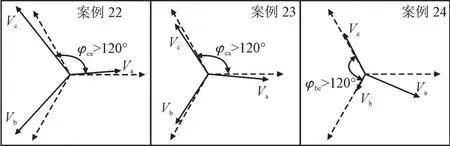
图2 与表2中3组案例对应的向量图Fig.2 Vector diagram corresponding to three cases in Table 2

根据TP-TA 法得出的130 个实测数据的暂降类型，有部分结果与其他算法不同。SCA 法与TP-TA 法结果不同的数量为72 组，以其中3 组为例，表3 和图3 给出了相关计算细节。

图3 与表3中3组案例对应的向量图Fig.3 Vector diagram corresponding to three cases in Table 3

表3 SCA法与TP-TA法结果不同的3组案例Table 3 Three cases with different results for SCA and TP-TA

案例25 是典型的Db类型暂降，a，b，c 三相电压幅值分别为0.81 p.u.，0.56 p.u.和0.73 p.u.。根据TP-TA 法，ΔIRV小于3，最小RV为RVa（RVa=0.19），相对角（φbc）为101.93°，小于120°，因此暂降类型为Ca型。

案例26 为Db型，a，b，c 三相电压幅值分别为1.19 p.u.，0.85 p.u.和0.94 p.u.。由于a 相的电压暂升，根据TP-TA 法，最小RV对应相为a 相，大小为0.19，导致其结果是Cc型暂降。

应用SCA 法和TP-TA 法计算案例27 的暂降类型，分别为Da和Cc。案例27 的a，b，c 三相电压幅值分别为0.85 p.u.，0.90 p.u.和0.95 p.u.。实际上该暂降的类型并不明显，由于a 相幅值最低，SCA法结果为Da类型，同时a 相和c 相之间的相角差小于120°，导致TP-TA 法的结果为Cc型。

5 TPA法

应用TPA 法计算21 组仿真数据1 的暂降类型，计算结果均为Da或Ca，在21 个计算结果中有9个错误结果，分别将第1、2、3、4、13、14、15、18、20组的结果判断为了Ca、Ca、Ca、Ca、Da、Da、Da、Da、Ca，见表4。β角是算法的核心指标，本文研究了特征电压幅值在0～90%的情况下β角的变化趋势，见图4，虚线和实线分别表示D 类和C 类暂降的β值。对于C 类和D 类暂降，β角的取值范围分别为-0.29～ -0.01 rad 和-0.84～-0.06 rad，当特征电压幅值增大时，β角的绝对值递减。由于大多数C 类和D 类暂降的β角都很小，因此β角作为判据中的一个参数，对算法结果的影响并不大。

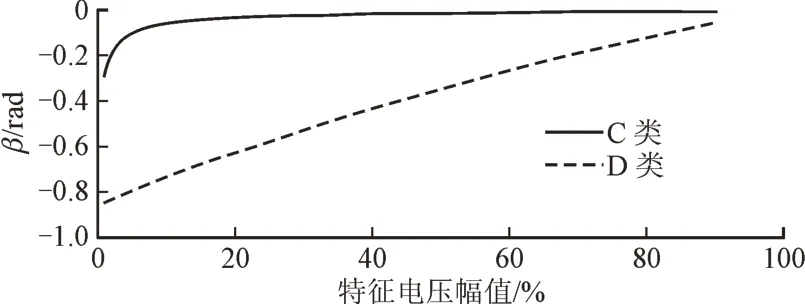
图4 暂降时β角的取值（无相位跳变）Fig.4 The value of β at voltage sag（without phase-angle jump）

为了说明TPA 的局限性，表4 列出了案例28和29，并配合仿真数据案例18 进行分析。案例28为没有发生暂降的三相平衡电压，案例29 为无相位跳变的Db类型电压暂降。表5 为相应的相电压和线电压相位。

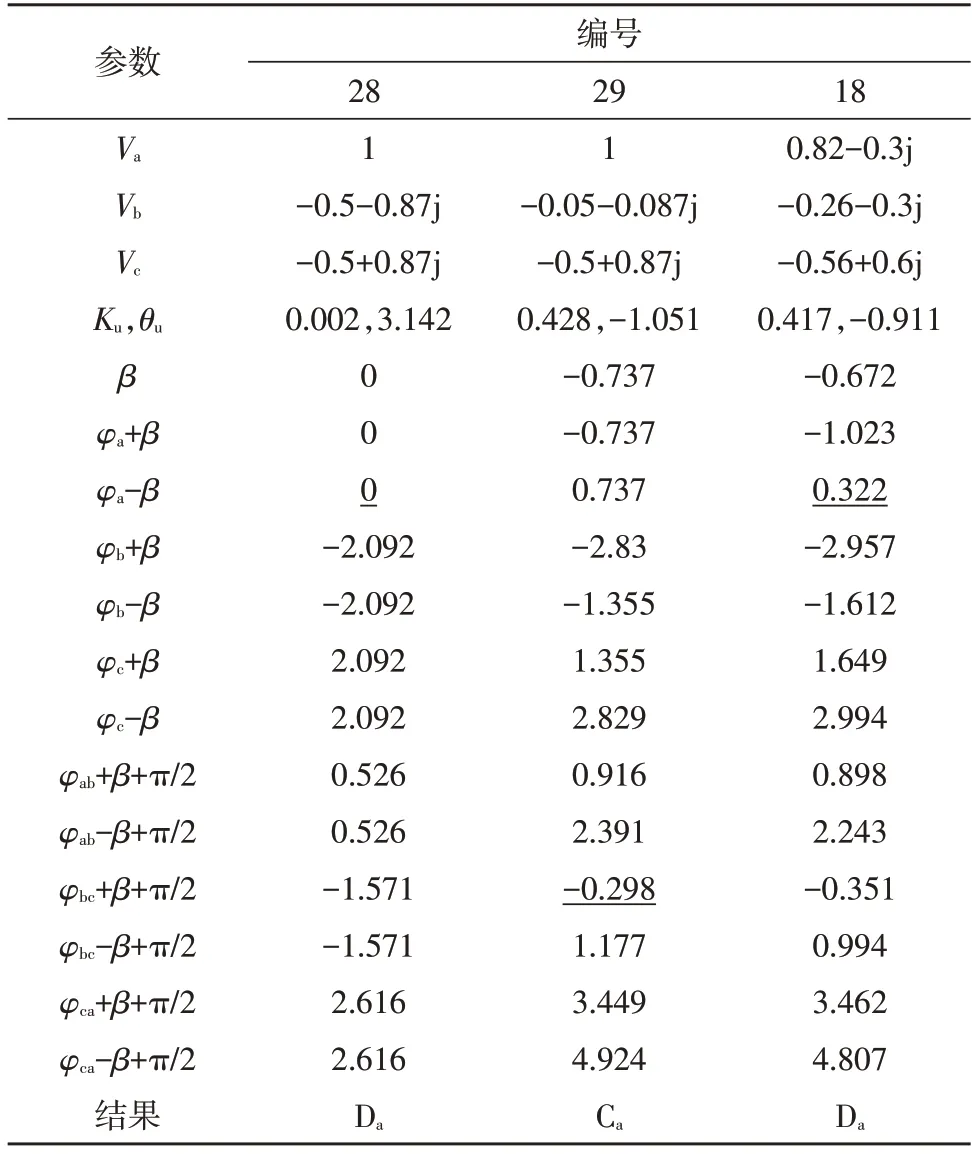
表4 3组案例计算结果Table 4 Calculation results of three groups of cases

表5 案例28和29的6个相角Table 5 Six phase angles of Case 28 and 29

案例28 的β角和φa均为0，因此|φa±β|为12个角中的最小值，对应暂降类型为Da，显然不正确。案例29 是典型的Db类型暂降，而在表4 中，最小角度为φbc+β+π/2，对应类型为Ca。来源于表1 的案例18 实际暂降类型为Db，而TPA 法的计算结果为Da。

验证后发现，当暂降类型为Db或Dc且没有伴随较大相位跳变时，φa，φb，φc大约分别为0，-2.09 rad（-120°）和2.09 rad（-120°），因此φa或φbc+π/2 的值总是最低的，见图5，这就是TPA 法发生误判的主要原因。

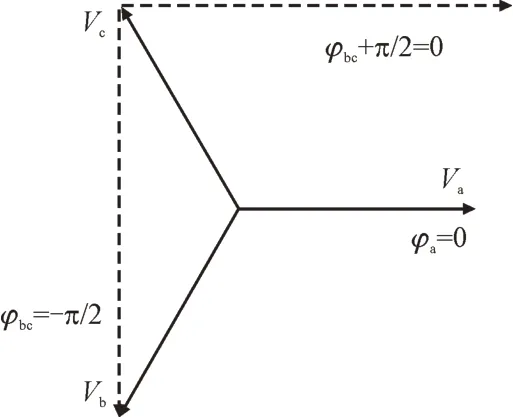
图5 φa和φbc+π/2向量图Fig.5 Vector diagram of φa and φbc+π/2

基于仿真数据2 的TPA 法计算结果见图6。当F为1 时，对于Db型仿真数据的验证结果如图6（a），正确率为0，其中黑色点集和灰色点集分别表示计算结果为Ca和Da类型的暂降。F为1 时，对于Cc型仿真数据的验证结果如图6（b），正确率仍为0。

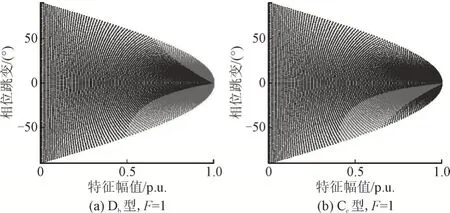
图6 TPA法验证结果Fig.6 Verification results of TPA method

从图6 可知，对于Db和Cc型仿真数据，TPA 法的计算结果总是Ca或Da型。

应用TPA 法计算216 组实测数据，结果为Ca，Da，Dc，Db类型的样本数分别为105，108，1 和2。以非Da和Ca型的3 组样本为例，见表6，图7 为相应的向量图。

图7 与表6中3组案例对应的向量图Fig.7 Vector diagram corresponding to three groups of cases in Table 6

表6 TPA法计算结果为Db或Dc的3组案例Table 6 Three groups of cases with result of Db or Dc by TPA method

案例30-32 的实际暂降类型分别是Cc，Cc和Cb，而TPA 法的结果是Db，Db和Dc，显然是不正确的。

根据以上分析，基于合成数据和实测数据的验证，表明该算法的结果几乎由φca+π/2 和φa值决定，易造成误判，因此不建议将TPA 法作为暂降类型的计算方法。

6 SVA法

应用SVA 法计算21 组暂降类型，有7 组计算错误，分别将第4、7、8、11、12、15、16 组的结果判断为了Cc、Dc、Dc、Dc、Dc、Dc、Dc，这7 组暂降的相位跳变都很大，可证明SVA 法对相位跳变较大的电压暂降非常敏感。图8 为案例4，7，8 的向量图，虚线表示暂降前正常的三相电压，实线表示案例中的电压暂降向量。其椭圆长半径的倾斜角分别为72.6°，162.5°，339.6°，见图9。根据长半径的倾斜角度可计算暂降类型，具体判据见图10。对于这3 组暂降，SVA 法的计算结果均错误。

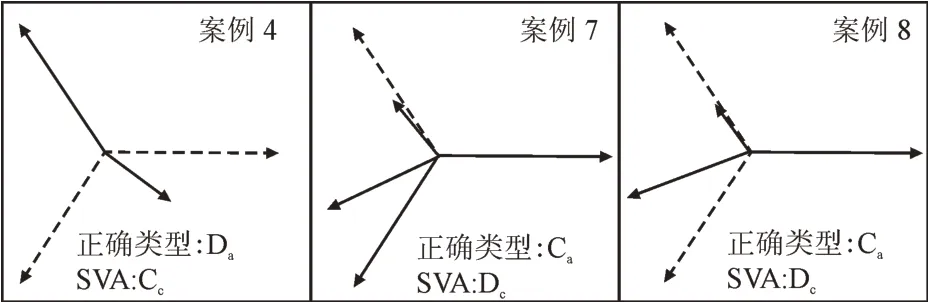
图8 仿真数据1中的3组案例向量图Fig.8 Vector diagram of 3 groups of cases from simulation data 1

图9 3组案例的椭圆倾斜角度Fig.9 Ellipse inclination angles of three groups of cases

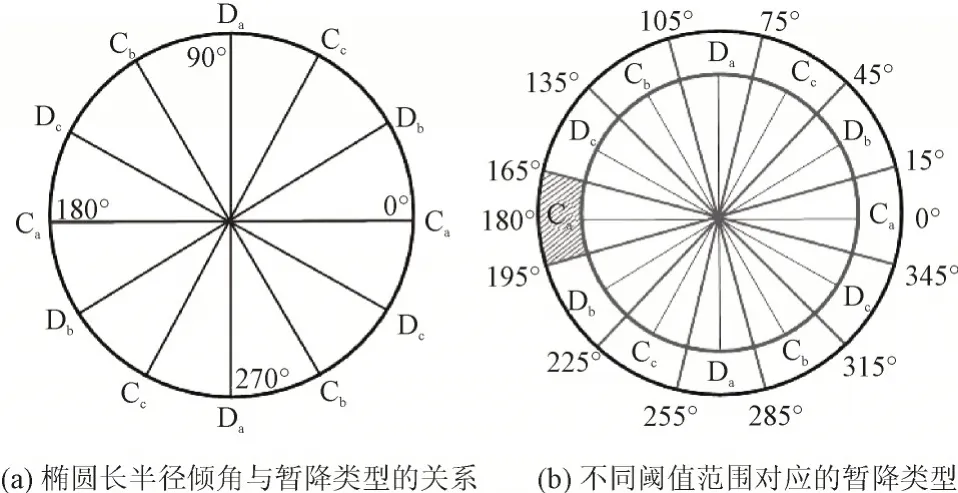
图10 基于SVA法的椭圆倾角判据图Fig.10 Ellipse inclination angle criterion diagram based on SVA method

案例4 的倾角为72.6°，属于Cc型（45°～75°），略低于Da型的阈值范围75°～105°。案例7 和案例8 的倾角分别为162.5°和339.6°，在Dc型角度阈值范围内（135°～165°和315°～345°），同时接近于Ca型阈值范围边界（165°～195°和345°～360°）。椭圆倾斜角受相角跳变的影响，最终可能导致暂降类型计算错误。为解决这一问题，也许可以通过类似于式（2）的方式修正不同类型的边界范围，从而改进算法。

基于仿真数据2 的SVA 法的验证结果见图11。对于相位跳变较大或暂降深度较浅的仿真数据，算法将会发生误判，由此证明SVA 法对相位跳变比较敏感，同时可以发现，正负序因子F也会影响SVA法的结果。

图11 SVA法验证结果Fig.11 Verification results of SVA

应用SVA 法计算216 组实测电压暂降，结果大致可分为3 类。第1 类，直观类型与算法结果相同；第2 类，直观类型与算法结果明显不同；第3类，无法区分数据的暂降类型。针对以上3 种情况，本节以案例33-35 作为分析对象，具体信息见表7 和图12。

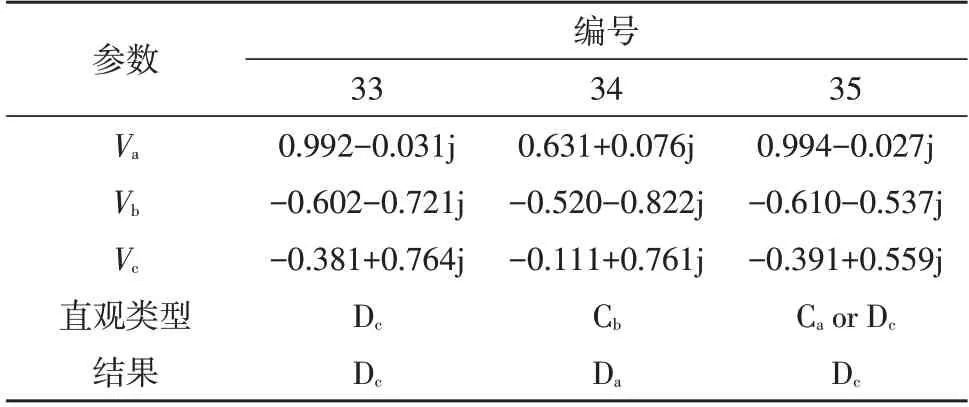
表7 SCA法与SVA法结果不同的3组案例Table 7 Three groups of cases with different results for SCA and SVA

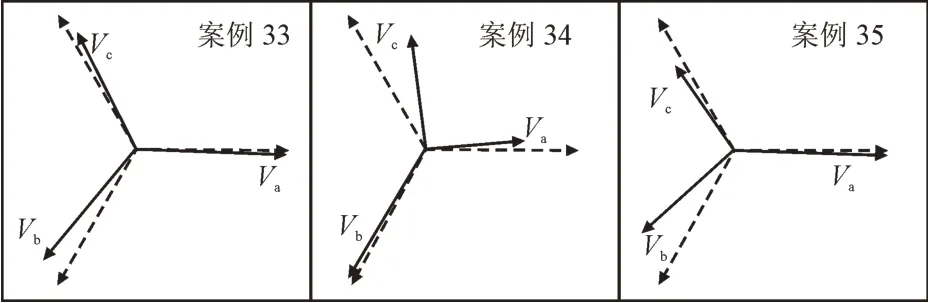
图12 与表9中3组案例对应的向量图Fig.12 Vector diagram corresponding to three groups of cases in Table 9

1）第1 类：案例33 的a、b、c 三相电压幅值分别为0.99 p.u.、0.94 p.u.和0.85 p.u.，由于c 相跌落的幅值几乎是其他2 相的3 倍，因此Dc类型较为合理。

2）第2 类：案例34 的直观类型与SVA 法结果明显不同。a、c 相的电压跌落幅值几乎相同，且远大于b 相跌落幅值，因此直观类型为Cb更为合理。该暂降的椭圆轨迹见图13，椭圆长轴角度为100.85°，根据SVA 法，其类型为Da，显然不正确。这是由于特征电压相位跳变的原因，导致长轴角度越过了Cb类型椭圆倾角的下边界105°。

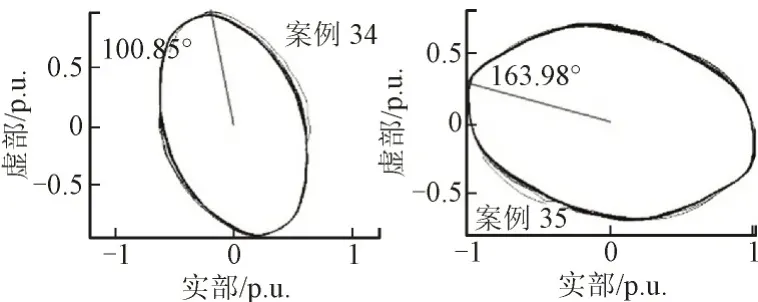
图13 两组案例的椭圆倾斜角度Fig.13 Ellipse inclination angles of two cases

3）第3 类：案例35 的a、b、c 三相电压幅值分别为0.99 p.u.，0.81 p.u.和0.68 p.u.。直观类型为Ca或Dc，很难确定其实际类型。而SVA 法的结果为Dc。由于相位跳变的原因，使得该案例的暂降类型难以直接判断。

7 算法改进建议

基于上述分析，现有方法都存在一些明显的问题，目前的算法还不能直接应用于监测系统，为电力公司和用户提供暂降类型信息，研究新的算法势在必行。

在新的分类算法研究中，应注意从以下方面进行改进：1）避免电压暂降相位跳变过大和跌落深度较浅引起的误判问题。可以以降低算法对相位跳变和跌落深度敏感度为目标，在保持计算准确率的基础上开发新算法。2）不同暂降类型的阈值选择也会对算法造成一定影响。为克服这一问题，可研究新的阈值选择标准，修正不同类型的边界范围，从而对算法进行改进。

8 结语

本文基于仿真数据和216 组实测数据，对5 种算法的计算结果进行了详细对比分析，得到以下结论：

1）SCA 和SPA 法受相位跳变和浅暂降的影响，可能会造成误判。特别是SPA 的准确率偏低，正负序因子F的减小不会影响SPA 法的准确率。

2）TP-TA 法的判据未能实现全面覆盖，对少数暂降数据不能得出计算结果，且当正负序因子F小于1 时，TP-TA 法的误判率将会升高，因此不建议将该算法应用于实际工程中。

3）TPA 法根据12 个角度中绝对值最小角作为暂降类型的计算依据，对于大多数没有较大相位跳变的电压暂降，φa和φbc+π/2 几乎都接近于0，这是TPA 法错误的主要原因，不建议应用。

4）对于大多数暂降，SVA 法的应用效果较好，但是该方法对相位跳变较为敏感，在较大相位跳变时不能得到正确结果。

在计算实测电压暂降类型时，受大相位跳变和正负序因子F的影响，各算法的结果存在较大差异，因此，后续研究的重点工作应是开发一种能够克服上述问题的算法，作为计算暂降类型的标准算法，应用到实际工程中。