基于遗传算法的不平衡电流保护调平方法的研究

李洁，林丽妲，张文军，尤鸿芃

（西安西电电力电容器有限责任公司，西安 710082）

0 引言

大容量电容器组常采用桥式不平衡电流保护作为电容器组内部故障保护。保护整定原则是当故障电容器完好元件过压达到一定水平时，不平衡保护报警或跳闸[1-3]。由于电容器单元的电容量存在随机偏差，因此在电容器组投运前就要求初始不平衡度接近于零[4]，以提高保护的灵敏度。

电容器组在检修后，由于桥臂电容量发生变化，可能导致电容器组的初始不平衡度变大，不符合电容器组的投运条件，此时就需要对电容器组中不同桥臂的电容器单元进行调换，使电容器组不平衡电流重新减小到符合投运条件，这一过程被称为电容器组的调平[5-8]。若调平的方案不合适，会显著增加工作量，浪费大量人力物力，特别是换流站交流滤波器装置等大型装置，还涉及登高操作。若需要大量的高空作业，还会增加施工的安全风险。因此，有必要设计一种既能满足不平衡电流要求，又能兼顾施工量和施工难度的计算方法。

为此，首先定量分析了初始不平衡电流的影响因素，以及初始不平衡度对保护灵敏度的影响，得出对初始不平衡度的要求；然后根据现场施工的要求，提出了方案的设计原则以及调平方案的优劣定量判断方法；在此基础上，基于遗传算法设计了电容器组调平方案的计算方法。经过验证，适当调整方案判断参数，可以得到保证不平衡度维持较低的水平，同时兼顾施工量和施工难度的调平方案。

遗传算法（genetic algorithm，GA）最早是由美国的John holland 于20 世纪70 年代提出，该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法[9-13]。该算法通过数学的方式，利用计算机仿真运算，将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程[14-17]。在求解较为复杂的组合优化问题时，相对一些常规的优化算法，通常能够较快地获得较好的优化结果[18-19]。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域，遗传算法在电力系统优化中已经有了很多应用[20-23]。

1 电容器组不平衡电流分析

1.1 不平衡电流保护的原理

不平衡电流保护的原理见图1，将电容器组分为容量相同的4 组，组成一个电桥结构。

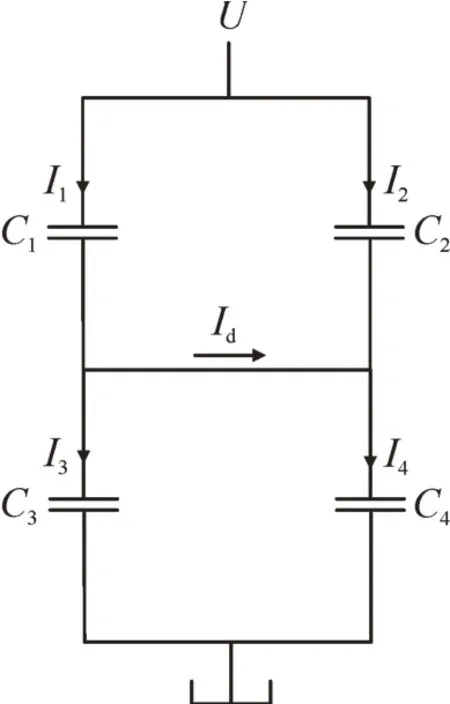
图1 不平衡电流保护原理图Fig.1 Principle diagram of unbalanced current protection

不平衡电流Id可以反映4 个桥臂电容的变量，则容易推导Id的表达式，公式为

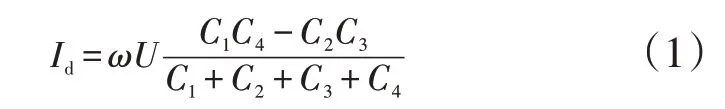
式中：ω为角频率；U为额定电压。

由式（1）可知，若4 个桥臂的电容量相等，则Id=0。设电容器4 个桥臂的理论电容量为C，4 个桥臂的偏差系数为k1～k4，C1=k1C，C2=k2C，C3=k3C，C4=k4C，设Iun为Id与电容器组电流IN的比值，则Iun如式（2）所示。Iun与电容器的额定电容量以及电压均无关，只与各个桥臂的偏差有关。

1.2 个体适应度计算

若一个电容器组在检修后更换了一台电容器，新电容器与被替换的电容器可能存在一定的电容量偏差，有时会导致初始不平衡度过大。此时，就需要调换不同桥臂的电容器，将不平衡电流控制在限定范围内，由于电容器数量巨大，这种调换方案的组合可以认为是无穷多。因此，满足工程需要即认为是可行的配平方案，对于配平方案的优劣从以下几点进行判断：

1.2.1 配平后的Iun

从保护可靠性的角度考虑，调整后的不平衡度越小越好，但电容器调换的工作量很大，特别是涉及电容器塔高处的电容器时，还具有安全隐患，所以实际中只要满足要求即可。可用式（3）对配平后的Iun进行评价。

式中：Ith为初始不平衡电流允许值；A为调节系数。

J1越小表示电容器配平越好，当Iun＞Ith时，J1迅速增加，当Iun=Ith时，J1始终为9，当Iun＜Ith时，J1变化较慢，J1符合对配平效果的评价要求，通过调节A可以调节曲线的变化速度。

1.2.2 需要调换的电容器数量

需要调换的电容器数量越大，则工作量越大，因此，配平方案需要调整的电容器数量越少越好。设可接受的调换数量为N0，方案的调换数量为N，则对于调换系数的评分如式（4）所示。

式中，B为调节系数。

N大于N0时，J2大于1 且迅速增大，N小于N0时，J2小于1 且变化较慢，可通过增加B来提高灵敏度。

1.2.3 需要调换的电容器位置

低处的电容器比高处的电容器更容易移动和操作，在效果相近的情况下，应有限调换低处的电容器。调换位置评分如式（5）所示。

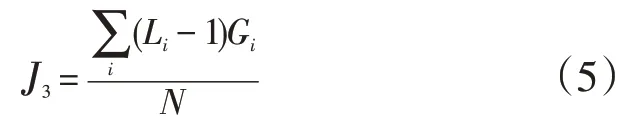
式中：L为层数，为不小于1 的整数；G为L层需要调换的台数。

基于上述3 点，用式（6）对配平方案进行评分。

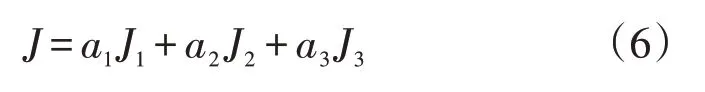
式中，a1、a2、a3为权重系数，用以调节3 个指标的权重，权重确定以后，J越小表示方案越好，权重越大表示对该指标变差的容忍度越低。

1.3 编码方式

首先将电容器组进行量化描述，见图2，每个位置P有4 个属性：所在的层数L，所在的串联段S，所在的桥臂M以及该位置的电容器单元U，U有2个属性：编号D和电容量C。

取如1.3.3各干燥层的样品（约5 g），分为3份，利用GB 5009.3—2016食品中水分的测定进行水分含量的测定，以湿基水分百分含量或干基水分含量表示。

图2 电容器组位置属性Fig.2 The attributes of position of capacitor bank

属性的具体含义见图3，P1至P4在相同的串联段，其S属性均为S1；P5至P8的S属性均为S2，S1串联段与S2串联段在L1层，故P1至P8的L属性均为L1；他们都在桥臂M1上，故M属性均为M1。一旦电容器组设置好以后，每个位置P的属性L、S、M均为固定值，只有电容器单元U可能发生变化。

图3 电容器位置组属性含义示意图Fig.3 Schematic diagram of the attributes of position of capacitor

1.4 染色体与基因

将电容器组的初始布置P01～P0n按照顺序形成初代染色体见图4，每个位置P即为一个基因，其按照某个顺序排列而成为一个染色体。

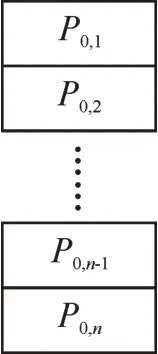
图4 染色体结构Fig.4 Structure of a chromosome

将电容器组中的电容器U随机布置x次，这x个染色体形成原始群落，见图5。

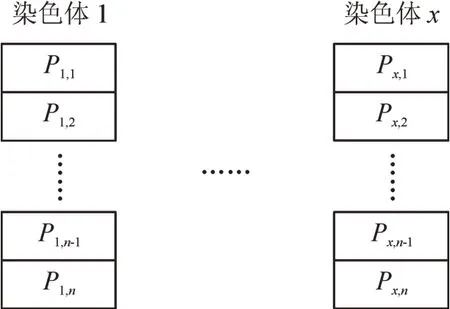
图5 原始群落Fig.5 Primitive community

由于实际中电容器的电容量不能变，只能改变其位置，因此本算法中只有交换操作，不涉及变异操作。

1.4.1 基因交换

原始群落中，随机选取2 个染色体，随机选择m个基因位置。

将染色体1 中随机位置基因的U提取并按照原有顺序组成交换序列1；并在染色体2 中寻找相同的U，按照其在染色体2 中的顺序组成交换序列2，将交换序列1 置于染色体2 的端部，将交换序列2 置于染色体1 的端部，即完成了一次基因互换，形成了2 个新染色体，见图6，该方法是一种典型的基因交换算法[24]。

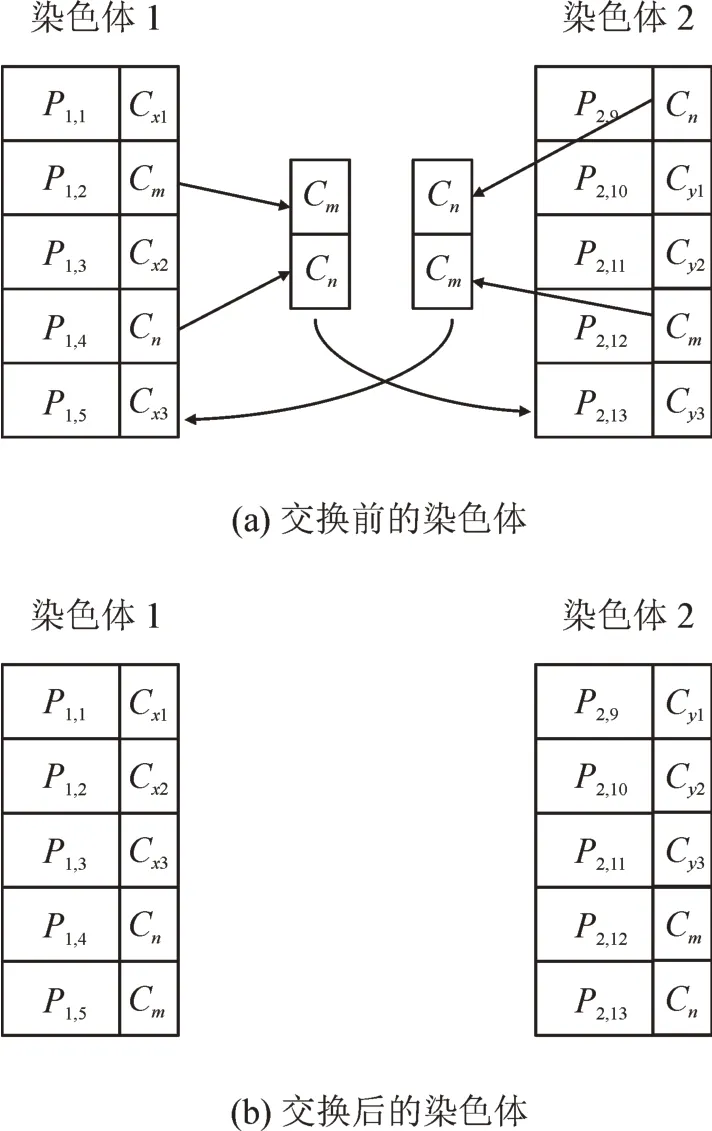
图6 染色体之间的基因交换Fig.6 Exchange of gene between 2 chromosomes

1.4.2 基因淘汰

通过基因交叉后最终形成x个新染色体，然后将新生成的染色体与原始群落染色体均进行个体适应度计算，将适应度最小的x个染色体作为新的原始群落，进行下一次基因交换，如此反复，直至新生成的染色体个体适应度达标，或者个体适应度不再降低为止。

图7 遗传算法调平的计算流程图Fig.7 Calculation flow chart of the leveling scheme of genetic algorithm

2 算法效果的验证

由式（2）可知，Iun仅与电容器的相对偏差有关，而与电压以及CU无关，假设一组电容器，分为2 个电容器塔，各9 层，每层8 台电容器，共有144 台电容器单元，采用1 并144 串的结构。电容器单元额定电容量为CU，服从以CU为期望值，1.8%CU为标准差的正态分布，随机生成144 个电容器，在电容量大于CU的电容器中，随机选择36 台构成桥臂C1，其他3 个桥臂由剩余的电容器随机组合构成，作为初始状态。初始状态的不平衡度Iun为0.76%，初始不平衡度不能超过0.5%。配平方案评分算法中，式（3）中A取4，式（4）中B取2。

2.1 厂内配平方案计算

厂内进行配平前，电容器单元未安装到组架上，对调整台数和位置无要求，希望方案的初始不平衡度越小越好，因此a2、a3设置为0，方案的评分收敛曲线见图8，收敛速度很快，迭代50 次时，方案的评分已经降低为10-8数量级，此时不平衡度为2.36×10-5%。

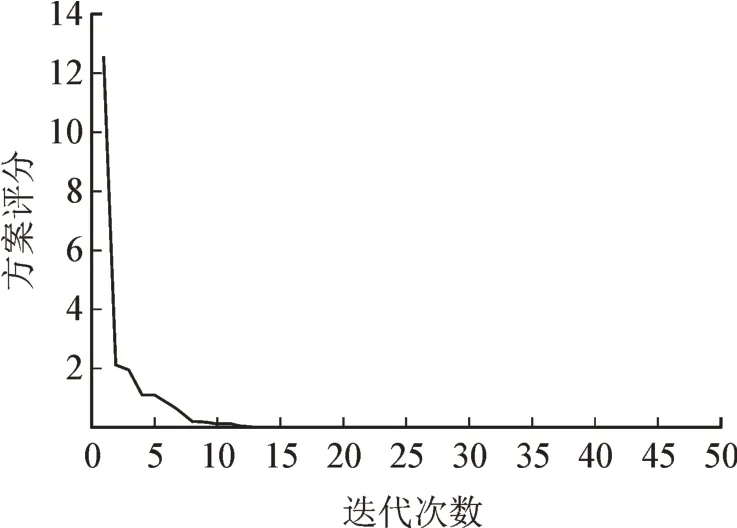
图8 厂内配平方案评分随迭代次数的变化曲线Fig.8 Variation curve of the score of leveling scheme in the factory with the number of iterations

2.2 现场配平方案计算

在工程现场，电容器已经安装上架，必须考虑调整的台数和位置，实现最经济、方便的方案。

2.2.1 希望调整数量较少

为了减少施工量，希望尽量减少调整的电容器的台数，则a1、a3取1，a2取10，允许的最大台数为10，调平方案的评分迭代见图9，调整后的不平衡度为0.27%，需要调整7 台电容器，其中第1 层3 台，第2 层2 台，第3 层2 台。

图9 倾向于调整数量少方案评分变化曲线Fig.9 Variation curve of scheme score favoring less adjustment

2.2.2 希望减少高空作业

若现场无合适的登高设备，则希望调平尽量在底层进行，则设a1、a2取1，a3取4，允许的最大台数为10，调平方案的评分迭代见图10，调整后的不平衡度为0.18%，需要调整8 台电容器，其中第1 层5 台，第2 层3 台。

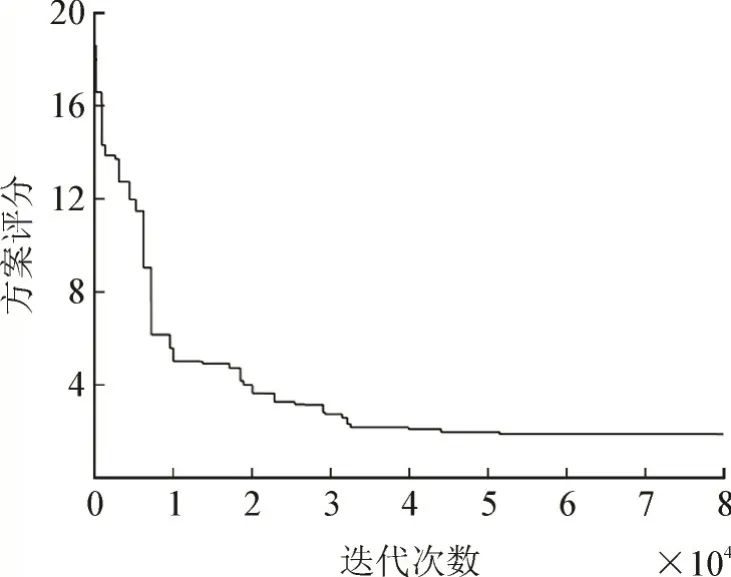
图10 倾向于低层调整的方案评分变化曲线Fig.10 Variation curve of scheme score favoring low level adjustment

由算例可知，在约束较少的厂内配平应用中，收敛仅需要数十次迭代，配平效果极好；而在现场使用中，增加了调试数量和位置的约束，收敛速度显著降低，需要大约5 万至10 万次迭代，普通计算机大约需要计算10～30 min，运算量较大，可以尝试加速收敛算法对其进行优化[25]。需要注意的是，由于基因的交换过程具有随机性，因此，同样的设置会得出不同的结果，需要不同的迭代次数，但最终都会得出一个相对符合要求的配平方案。

3 结语

根据工程经验与需求，设计了评价电容器组配平方案的量化方法，基于遗传算法的思想，设计了适用于电容器组描述的基因、染色体以及基因交换算法，用3 种不同的工况对算法效果进行了验证，得出如下结论：

1）根据不同的需要设置对不平衡度、调整数量以及调整层数的权重，所设计的算法可以计算出合适的配平方案。

2）可以根据实际需要调整对配平方案的评价算法，以实现对超出预期目标的容忍度的调节。

3）不考虑调整数量和调整层数时，算法收敛极快。增加对调整数量和调整层数的约束后，收敛变慢，运算量大幅度增加，完成计算可能需要10～30 min，甚至更长，会影响现场使用效果。

4）下一步可以考虑优化基因交换算法，减少无意义的基因交换以提高收敛速度，改善使用效果。