基于SABSO 算法的含分布式电源配电网故障定位
骆通,何晋,管恩齐,杨凡,曹鲁成,周石金
(1.云南民族大学电气信息工程学院,昆明 650000;2.国网山东省电力公司单县供电公司,山东 菏泽 274300)
0 引言
越来越多的风力发电、光伏发电和水利发电等分布式电源接入配电网[1-2],使得配电网由原来的单电源供电变为多个电源供电,配电网的结构发生变化,更加复杂[3-4]。当配电网的某个地方发生故障时,流过故障点的电流除了来自于系统电源外,还来自于分布式电源,功率也可能发生倒向,使故障定位的难度增加[5]。
目前故障定位的算法主要有两大类,一类是基于馈线终端装置(feeder terminal unit,FTU)的矩阵算法[6],矩阵算法容错较差,对FTU 上传的故障信息准确性要求比较高,如果FTU 上传的信息发生畸变,则容易导致误判,无法正确识别故障区段。另一类是基于馈线终端装置检测的智能算法,包括粒子群算法[7]、遗传算法[8]、蚁群算法[9]、蝙蝠算法[10]、神经网络算法[11]等。文献[7]采用的方法收敛速度快,但容易陷入局部最优。文献[8]对解空间进行协同搜索,提高了收敛效率。但交叉变异概率为定值,不能随个体适应度值的大小自动调整。文献[9]采用的方法需要设置合适的参数,否则收敛效果不好。文献[10]采用的方法同样有些依赖参数的调整,同时后期收敛速度可能会变慢。文献[11]采用的方法在识别双重故障进行故障定位时正确率不够高。
针对上述问题,提出了一种模拟退火算法和天牛群算法相结合的算法,并将此算法应用到含分布式电源配电网的故障定位中。利用Matlab 进行仿真,检验提出的算法,并与其他算法进行比较,结果证明了该算法在的优势。
1 算法原理
1.1 天牛群算法原理
天牛群优化算法[12]是2020 年提出的一种用于全局寻优的智能算法,结合甲虫觅食机制和群体优化算法,具有良好的鲁棒性和运行速度,本文借鉴此算法,将天牛须算法和粒子群算法相结合。天牛须算法[13-14]是2017 年提出的一种用于全局寻优的智能算法,来源于天牛寻找食物的过程,天牛须算法是模拟一只天牛寻找食物的过程,天牛的左右须可以感受到食物散发的气味浓度,天牛判断左须和右须感受到的浓度差别来决定下一步移动的方向,以此类推,直到找到食物为止。天牛须算法不需要了解具体公式,不需要梯度信息,就可以实现高效全局寻优。群体化后各天牛之间可以进行信息共享,使收敛速度加快。
天牛群算法的原理如下所示:
1)假设天牛群中天牛个数为N,待优化问题变量维数为D,初始化天牛群的位置为X、速度为V,且X和V都是N×D的矩阵,第i个天牛的速度向量为Vi=Vmax(V1,V2,V3,…,Vn),位置向量为Xi=(X1,X2,X3,…,Xn)并确定个体最优Pbest和全局最优Gbest。
2)利用式(1)来更新速度,并利用式(2)对速度进行归一化处理,求得天牛右须指向左须的朝向:


3)根据朝向,由式(3)可得第i个天牛的左须位置,由式(4)可得第i个天牛的右须位置:

式中,d为天牛左须和右须之间的间距。
4)根据第i个天牛的左须位置和右须位置,可求的天牛左须和右须的适应度函数值fl和fr,fl=f(xl),fr=f(xr),并按照式(5)来更新第i个天牛位置,公式为

式中,d表示步长。
5)判断迭代次数,如果迭代次数达到要求,则迭代完成,否则按照式(1)至式(5)继续迭代。
1.2 模拟退火算法
模拟退火算法[15]的基本思想来自物理退火过程,该过程主要由以下几个组成部分:加温过程、等温过程和冷却过程。
该算法的具体流程如下:
1)设置初始温度T0(根据具体情况充分大)、初始解状态X0、每个温度T值需要迭代的次数为L。
2)对k=1,2,3,…,L,重复第3)步至第6)步。
3)产生新的解状态X′。
4)计算增量ΔE,ΔE=E(X′)-E(X),其中E(X)为构造的评价函数。
5)如果ΔE小于0,则接受X′作为新的当前解,否则以概率exp(-ΔE/T)接受X′作为新的当前解。
6)如果满足终止条件,则输出当前解作为最优解,结束程序。
7)T渐渐降低,且T趋近与0,然后转第2)步。
1.3 基于模拟退火的天牛群算法
由于天牛须算法和粒子群算法结合仅仅是让天牛群体化,实现信息共享,增加其搜寻的效率,可以更加快速地找到最优的目标,但在一定程度上仍然不能避免其陷入局部最优。所以,在此基础上,引入模拟退火算法,可以避免其陷入局部最优。
该算法是以天牛群算法为主体算法,同时引入模拟退火机制。
其算法步骤如下:
1)初始化天牛群的位置和速度后,求得个体最优解和全局最优解,比较两个最优解并保留更优解,然后,确定初始温度T0,计算公式为

2)根据式(7)确定当前温度下各天牛的适应值。

3)根据式(8)、式(9)以一定的概率,从所有的天牛中确定全局最优的替代值。

4)接着按照式(1)-式(5)更新个体最优和全局最优,然后进行退温操作。

式中,lamda 为降温速率。
当算法满足迭代次数,则停止迭代,输出最优解,否则返回公式(7)继续计算。
算法的流程图见图1。

图1 SABSO算法流程图Fig.1 Flow chart of SABSO algorithm
2 基于模拟退火的天牛群算法在含分布式电源配电网故障定位的应用
配电网发生故障后,收集安装在配电网各线路开关处的FTU 在故障发生时上传的故障电流信息,进行二进制编码,然后计算开关函数和适应度函数,并通过算法逐次迭代,找到最优解,即故障位置。
2.1 编码方式
对FTU 上传的故障电流信息进行二进制编码,一般的单电源电路的线路故障电流信息可以用二进制编码“0”或“1”来表示,但是含有分布式配电网的线路故障则无法用二进制编码“0”或“1”来表示,因为分布式电源的并入,使得故障点的电流不仅仅来自于配电网的系统电源,还可以从分布式电源流入故障点。所以我们用“1”,“0”,“-1”来表示故障电流信息[16],假定从系统电源流向各区段的方向为正,这样可以得出:

式中,Ij(j=1,2,3,…,N)为第j个开关状态的编码,N为开关总个数。
2.2 开关函数
本文采用文献[17]中的开关函数,应用于含分布式电源配电网的故障定位,开关函数为

式中:“Σ”为逻辑或运算;M和N分别为以编号为j的开关为分界点的上游配电网和下游配电网中线路区段的数目;KS1为上游配电区域的系统电源是否接入配电网,KS2为下游配电区域的分布式电源是否接入配电网电源的开关系数,“0”代表没有接入,“1”代表接入;Xj,s1和Xj,s2分别为编号是j的开关到上游配电区域的系统电源或分布式式电源和到下游配电区域的分布式电源的路径上所经过的所有线路区段的状态值;Xj(n)和Xj(m)分别为以编号是j的开关为分界点的上游配电网和下游配电网中线路区段的状态值。
2.3 适应度函数
适应度函数对算法能否得到最优解即配电网能否准确定位起着决定性作用,文献[18]提出适应度函数,该适应度函数是单电源配电网故障定位常用的适应度函数,同时也适用于含分布式电源的多电源配电网的故障定位,具体公式为
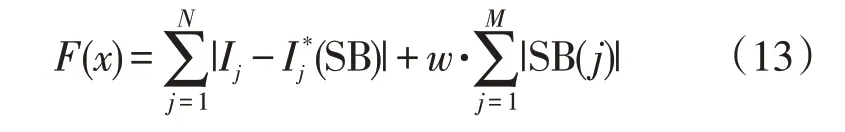
式中:Ij为FTU 上传的第j个开关的状态信息;I*j(SB)为第j个开关的期望状态;N为配电网开关总个数;M为配电网馈线总数;SB(j)为区段状态编码,“1”代表该区段有故障,“0”代表该区段没有故障;w为设置的系数,取值为[0,1]之间的正实数,本文取w=0.5。
3 算例分析
本文采用如图2 所示的典型33 节点含分布式电源配电网。其中S 代表系统电源,DG1、DG2、DG3代表3 个接入的分布式电源,K1、K2、K3代表3 个分布式电源与配电网的开关,0 表示分布式电源没有接入配电网,1 表示分布式电源接入配电网;1-33 为开关的节点编号,(1)-(33)为相对应的线路区段编号。本文采用Matlab2019a 来对基于模拟退火的天牛群算法进行编程,具体参数设置如下:种群数目N=100,维度为D=33,天牛加速因子w1=1.6 和w2=1.445,最大迭代次数M=50,初始温度T,Vmax=3,降温速率lamda=0.6,每个温度迭代N次,步长δ=10,两须之间的距离d=1,惯性常数eta=0.95。

图2 含DG的33节点配电网模型Fig.2 33-node distribution network model containing DG
3.1 单区段故障仿真
假设配电网在线路的不同位置发生单区段故障,在考虑分布式电源是否接入配电网以及各线路上FTU 上传的各分段开关的信息是否发生畸变等不同情况进行仿真,测试结果见表1。

表1 单重故障仿真结果Table 1 Simulation result of single fault
由表1 可以看出,当发生单区段故障时,无论FTU 上传的各分段开关的信息是否发生畸变,以及分布式电源是否接入配电网,模拟退火天牛群算法都可以准确识别出故障区域。
3.2 多区段故障仿真
现实生活中,两个区段及以上同时发生故障以及FTU 上传的各分段开关的信息发生畸变的概率很低,为了充分测试算法的性能,所以进行配电网多区段故障仿真,假设配电网在线路的不同位置发生多区段故障,在考虑分布式电源是否接入配电网以及各线路上FTU 上传的各分段开关的信息是否发生畸变等不同结果进行仿真,测试结果见表2。

表2 多重故障仿真结果Table 2 Simulation result of multiple faults
由表2 可以看出,当发生多区段故障时,无论FTU 上传的各分段开关的信息是否发生畸变,以及分布式电源是否接入配电网,模拟退火天牛群算法都可以准确识别出故障区域。
3.3 算法性能对比
在参数设置相同条件下,分布式电源接入情况为K1=1、K2=1、K3=1,分别采用模拟退火粒子群(SAPSO)算法、天牛群(BSO)算法和模拟退火天牛群(SABSO)算法对以下情况进行模拟仿真,对比图见图3。
1):馈线(8)发生故障,无信息畸变;
2):馈线(8)发生故障,6 号开关处FTU 上传的信息发生畸变;
3):馈线(8)(20)发生故障,无信息畸变;
4):馈线(8)(20)发生故障,6 号和18 号开关处FTU 上传的信息发生畸变。
从图3 可以看出,在以上4 种情况下,3 种算法均可以达到理想的适应度值。模拟退火天牛群算法的收敛速度明显快于模拟退火粒子群算法的收敛速度,也比天牛群算法的收敛速快。并且,随着故障难度的提升,模拟退火粒子群算法和天牛群算法的迭代次数都会有小幅度的增加,大致上,在单一故障的情况下,模拟退火天牛群算法在迭代4 次左右就可以寻得最优解,而天牛群算法和模拟退火粒子群算法则分别需要迭代6 次和10 次左右。而在多重故障的情况下,模拟退火天牛群算法依然可以在迭代4 次左右就可以寻得最优解,而天牛群算法和模拟退火粒子群算法则分别需要迭代7 次和12 次左右。
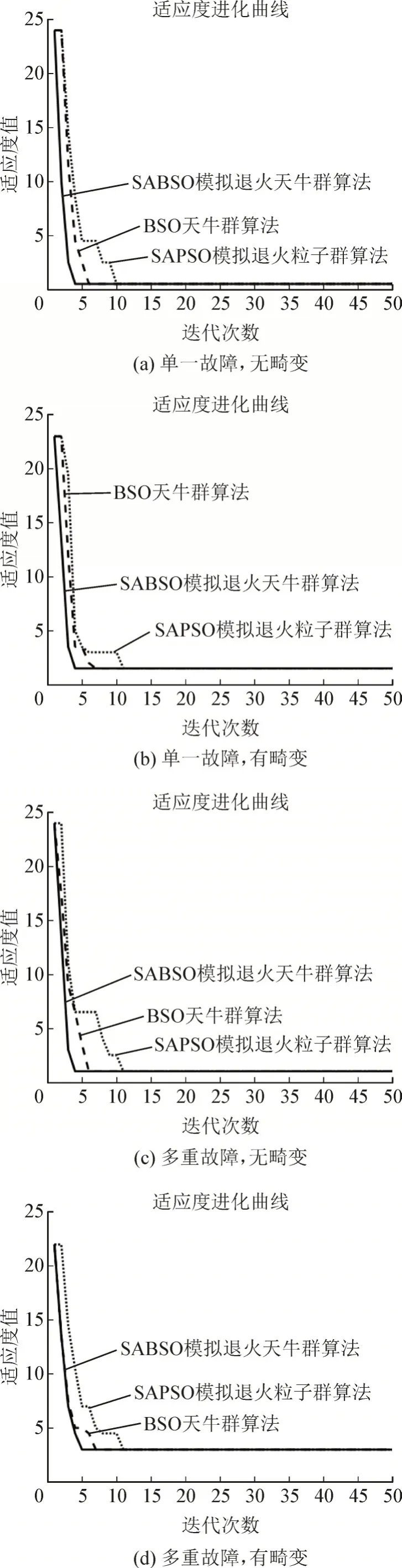
图3 算法仿真对比图Fig.3 Comparison diagram of algorithm simulation
3.4 算法准确率对比
针对图3 的4 种情况,分别用模拟退火粒子群(SAPSO)算法、天牛群(BSO)算法和模拟退火天牛群(SABSO)算法进行模拟仿真,每种情况均仿真20次,结果见表3。

表3 3种算法故障定位正确率对比Table 3 Comparison fault location accuracy of three algorithms
由表3 对比可得,SABSO 算法在故障定位中的准确性高,即使存在信息畸变,准确性也高,具有高容错性,比较可靠。相比于该算法,BSO 算法在故障定位中正确率也较高,但在信息畸变的多重故障情况下,正确率不如SABSO 算法,而SAPSO 算法随着故障难度的提升正确率在不断下降。
4 结语
本文利用模拟退火天牛群算法实现了对含分布式电源配电网的故障区间定位,并通过Matlab 验证了该算法在含分布式电源配电网故障定位中的优势。
该算法融合了天牛须算法的高效性,粒子群算法的信息交流以及模拟退火算法的可靠性,可以快速准确地求得全局最优解,避免陷入局部最优。在单区段和多区段发生故障甚至FTU 上传数据发生畸变等复杂情况下,通过Matlab 算例仿真,验证了该算法的有效性、快速性和容错性,这为含分布式电源配电网以及更复杂配电网故障定位的深入研究提供了新的思路。

