基于系统辨识的滑行艇回转运动模式研究

刘 曼，岳宗杰，于 博

渤海船舶职业学院，辽宁 兴城 125105

在船舶操纵性方面，国内外已经取得了很多成果[1-2]。通过查找文献，发现近些年对滑行艇操纵性方面进行研究的主要有：荷兰德尔福特科技大学、美国戴维逊水池、日本大阪府立大学、中国船舶科学研究中心、哈尔滨工程大学、江苏科技大学等。

70 年代以来，随着现代控制理论学科的不断发展，船舶专业的研究人员开始应用此门学科中的参数辨识技术来研究船舶操纵性。这种方法是通过实船或船模自航实验中测定的输入（操舵） 数据和输出（船舶各运动参数） 数据，对待辨识方程中的各系数进行辨识。近几年，系统辨识逐渐被应用于船舶实验研究领域[3-4]，辨识技术主要用来识别操纵性运动的水动力导数。但从国内外研究现状和趋势来看，对滑行艇回转运动模式系统辨识的研究仍不多。本文以滑行艇模型回转实验为基础，通过改变舵角和航速，运用系统辨识程序分析处理实验数据，建立滑行艇操纵性数学模型，同时运用编制的C#程序，对数学模型中的实验数据进行辨识，进而研究滑行艇的回转性能。

1 操纵性回转实验

1.1 模型简介

本实验以防滑行面飞溅（沿滑行艇中部舭部到艇体尾部横向方向安装防飞溅片） 的无人滑行艇为模型，实验模型的主尺度如下：艇长1.5 m，艇宽0.46 m，型深0.19 m，设计吃水0.13 m，设计排水量50 kg，设计航速5 kn。

该模型艇装有新型USV 智能控制体系，人机交互界面可以实时显示USV 的位置、姿态及环境感知信息。本艇以PAC（Programming Automatic Controller） 作为核心控制器，三维电子罗盘和DGPS 组成导航定位系统，通过无线数传电台传输数据。

1.2 实验方案

本次回转性实验是在室外水池进行的。本次实验为自航实验，整个实验过程均由PAC 作为控制器，速度舵角控制器控制舵角。通过变化电压，控制不同航速，改变舵角，进行不同航速、不同舵角下滑行艇的组合实验。艇模的航速、位置、艏向角等信息可以通过艇模上搭载的导航定位系统采集。

1.3 回转实验数据与分析

实验所得回转数据如表1 所示。

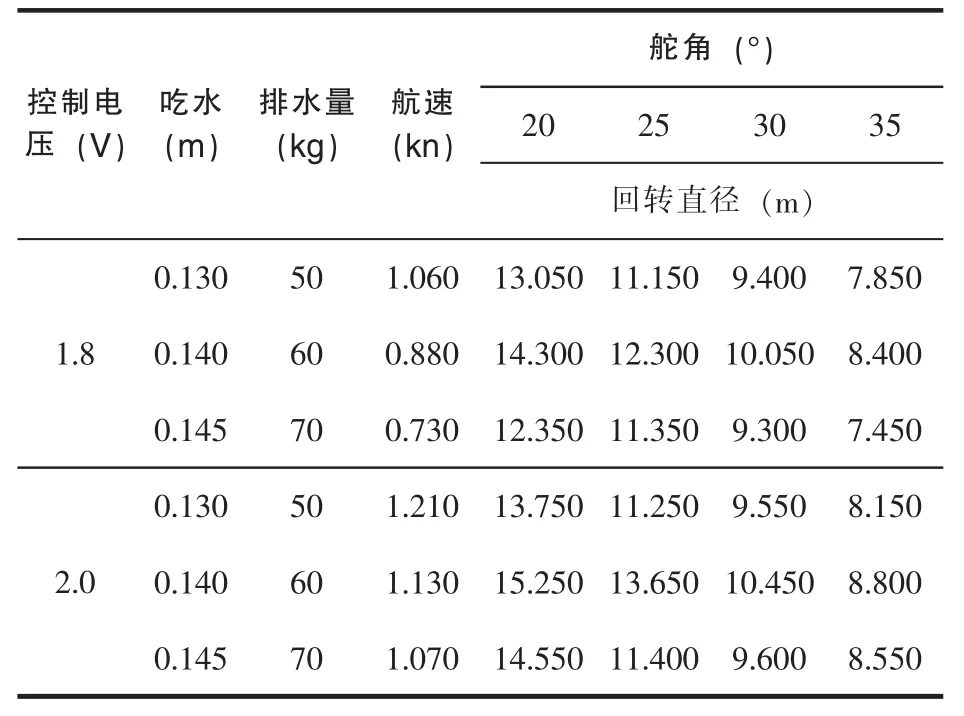
表1 回转实验数据

从表1 可以看出，航速随着控制电压的增大而逐渐增大。船模进入定常回转运动后，比直线运动时的速度小。吃水越大，航速越小。图1 给出了1.8 V 电压下，三种不同吃水状态的回转直径随舵角的变化。吃水从0.13 m 变化增大到0.14 m 的过程中，回转直径整体增大，且回转直径随舵角线性递减。吃水从0.14 m 增大0.145 m 的过程中，回转直径呈现减小趋势，但在25 度舵角时，该状态下的回转直径比最小吃水时对应的回转直径大。

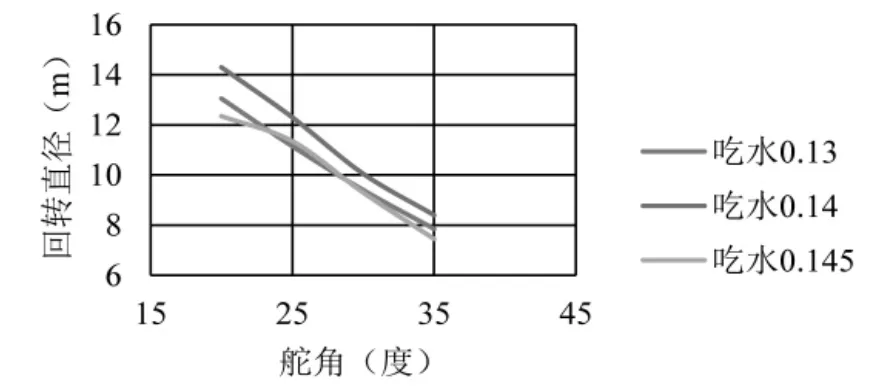
图1 回转直径随舵角变化曲线 （控制电压为1.8V）

图2 给出了控制电压为2 V 时，三种不同吃水状态下，回转直径随舵角的变化情况。吃水从0.13 m 增大到0.14 m 的过程中，对应的回转直径整体增大，且回转直径随舵角递减。吃水从0.14 m 增大到0.145 m 的过程中，回转直径整体呈现减小趋势。但随舵角的增大，三种不同吃水下的回转直径均呈现递减变化。

图2 控制电压下回转直径随舵角变化曲线 （控制电压为2V）

从以上两幅图可以看出，在电压不变的情况下，舵角越小，滑行艇回转直径越大；相反，舵角越大，船模回转直径越小，且回转直径随舵角基本呈线性关系变化。

2 滑行艇操纵性数学模型

2.1 数学模型

一个好的船舶操纵运动的数学模型，应尽可能准确地描述船舶的实际航行状态，且模型中的参数应尽可能少，同时，每一个参数应具有明确的物理含义。本文将选取两个数学模型，并将辨识结果进行对比，从而确定最优模型。

数学模型一：

参考劳贝公式，当舵展弦比大于1 时，船舶的定常回转直径：

式中，k1为随变化的参数，k2为随舵角δ变化的参数。

本模型船取 C=1.2，相对回转直径DL＝DS／L，将相对回转直径公式表示为：

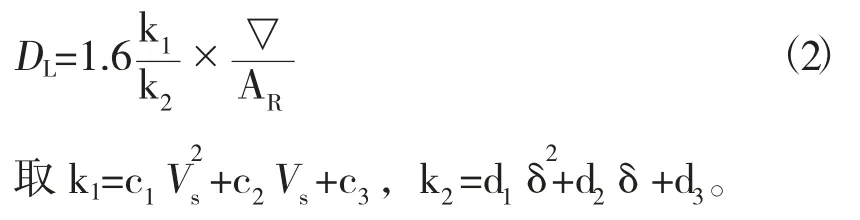
设回转运动目标函数为F，则回转辨识模型可以表示为：

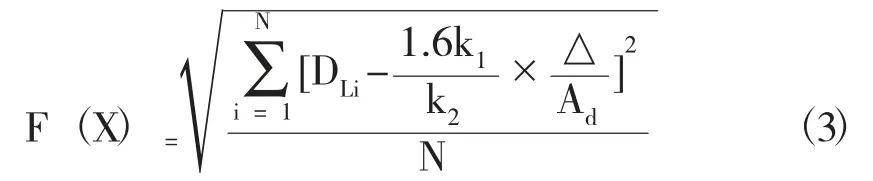
式中，DLi为第i 时刻的船模定常回转直径(m)，△为船模排水量（t），Ad为舵面积（m2），N 为实验采集数据组数。

经计算比较，可将约束条件设定为：

c1[0,0.1]，c2[0,1]，c3[0,1]，d1[0,10],，d2[0,10]，d3[0,10]。选定 c1，c2，c3，c4，d1，d2，d3为优化参数，并对其进行辨识。

数学模型二：

参考江田公式，高速船的船速效应：

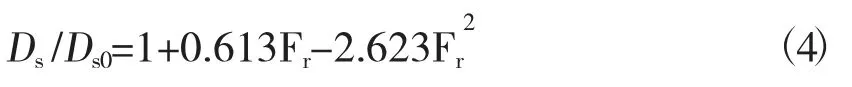
式中，Ds0为Fr≤0.25 时的回转直径。依据公式（4），根据实验数据中回转直径D与舵角δ成负相关的关系，采用拟合多项式的方式构造回转运动辨识数学方程，以保证辨识精度。

将相对回转直径公式表示为：

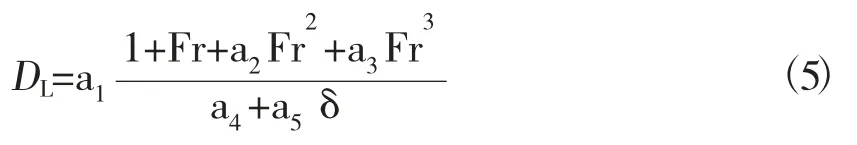
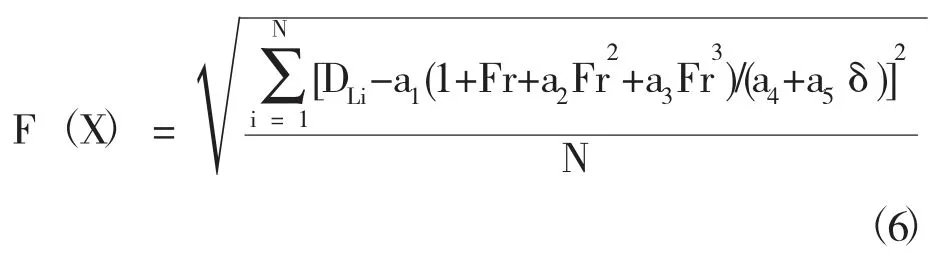
式中，a1，a2，a3，a4和 a5为参数，N 为实验采集数据组数。

经计算比较，可将约束条件设定为：

a1[0,0.1]，a2[0,1]，a3[0,1]，a4[0,10]，a5[0,10]。选定a1，a2，a3，a4，a5为优化参数，并对其进行辨识。

2.2 辨识方法

本文采用遗传算法确定参数，应用C#语言改编的“无人艇操纵运动系统辨识程序”，对待定参数进行辨识。计算工况设置如下：遗传算法种群数200，迭代次数2 000，交叉概率0.8，变异概率0.15，选择内层载波的方法进行计算。

数学模型一：舵面积Ad为0.026 4 m2，系统辨识输入量为航速、舵角δ、排水量和相对回转直径DLi，输出量为各辨识参数 c1，c2，c3，d1，d2，d3。

数学模型二：系统辨识输入量为δ、弗鲁德数Fr 和DLi，输出量为 c1，c2，c3，c4和 d1，d2，d3，d4。

2.3 系统辨识计算

将实验数据分别导入两种数学模型系统辨识程序中，设置算法参数后，进行辨识计算，选取最优结果。回转性系统辨识界面如图3 所示，得出辨识结果如下：

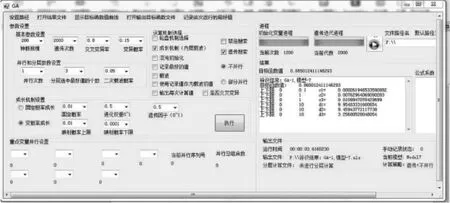
图3 回转性系统辨识界面

模型一：c1=0.000 262，c2=0.007 63，c3=0.010 995，d1=9.954833，d2=9.459438，d3=3.256805，根据结果得出回转直径表达式：

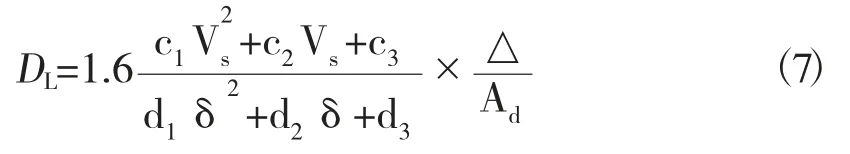
模型二：a1=0.058 386，a2=0.147 272，a3=0.836 367，a4=0.001 02，a5=0.017 654，根据结果得出回转直径表达式：

2.4 数据处理与分析

将辨识结果与实验数据进行对比，处理结果如图4 和图5 所示。

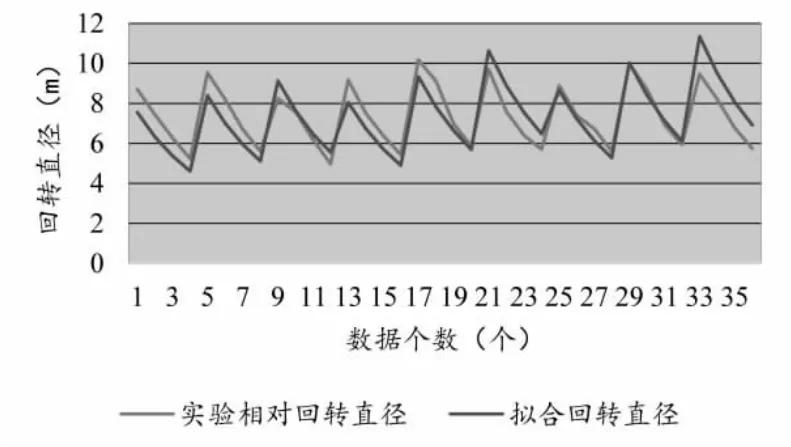
图4 第一组数据辨识结果与实验结果对比

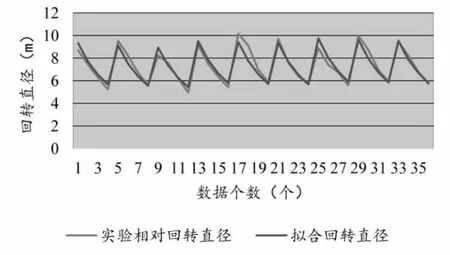
图5 第二组数据辨识结果与实验结果对比

对比图4 和图5 发现，数学模型一误差较大，而数学模型二除一组数据的辨识相对误差较大之外，其他数据的辨识相对误差绝对值均低于10%，说明采用该辨识模型得到的辨识结果与实验结果吻合度较好。产生这种结果的原因如下：

1） 该类型的具有防飞溅片的滑行艇，航速对回转直径的影响较为敏感，在模型一中，相对回转直径与航速的关系用二阶非线性方程表示，而在模型二中，相对回转直径与航速的关系用三阶非线性方程表示，故模型二与实验数据拟合性较好；

2） 由实验数据和定常回转直径随舵角变化关系曲线（图1，图2） 看出，定常回转直径随舵角基本呈线性关系变化，而模型一中取k2=d1δ2+d2δ+d3。，即相对回转直径与舵角呈二阶非线性关系变化，故模型一与实验数据误差较大；

3） 实验过程中回转直径测量存在一定的误差，且两次实验间隔时间较短，水面存在余波，对实验数据的精度存在一定的影响，故实验数据中存在一些误差较大的点。

综上，最终选择的模型艇回转运动数学模型如下：

3 结论

本文通过基于遗传算法的优化程序对滑行艇操纵性回转运动模式的相关参数进行了辨识，对比分析两种数学模型，选出了与实验数据拟合性较好的数学模型，辨识所得模型可以分析回转直径的变化情况，即对系统输出量未来的变化情况进行预测。

本文采取模型实验与系统辨识相结合的方法，可对同类型无人滑行艇的操纵性运动进行预报，同时可为同类型具有防滑行面飞溅片体的滑行艇艇型的设计和其操纵性方面研究提供借鉴。但由于浅水效应，且目前对此类滑行艇数学模型的理论研究不够深入，本文采用的数学模型均取自于经验公式，故所得两组辨识结果差别较大，对转化到滑行艇上的应用，还有待进一步研究。