对2022年全国乙卷理综第25题第2问的深入探究

于海滨

（东北师范大学附属中学，吉林长春 130021）

题.如图1（a）所示，一质量为m的物块A 与轻质弹簧连接，静止在光滑水平面上，物块B向A运动，t=0 时与弹簧接触，到t=2t0时与弹簧分离，第1次碰撞结束，A、B 的图像如图1（b）所示，已知从t=0到t=t0时间内，物块A 运动的距离为0.36v0t0.A、B 分离后，A 滑上粗糙斜面，然后滑下，与一直在水平面上运动的B再次碰撞，之后A 再次滑上斜面，达到最高点与前一次相同，斜面倾角为θ（sinθ=0.6），与水平面光滑连接，碰撞过程中弹簧始终处于弹性限度内，求

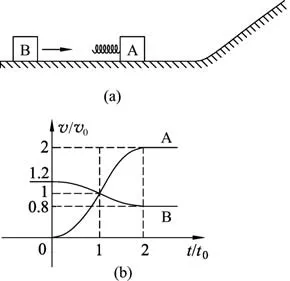
图1

（1）第1次碰撞过程中，弹簧弹性势能的最大值.

（2）第1次碰撞过程中，弹簧压缩量的最大值.

（3）物块A 与斜面间的动摩擦因数.

解析：通过第（1）问我们可以解得mB=5m，且弹簧弹性势能的最大值Epmax=0.6mv02，下面重点来看第（2）问.

解法1：采用微元法类比人船模型的处理方法.

5m·1.2v0·Δt=5mvB1·Δt+mvA1·Δt，

5m·1.2v0·Δt=5mvB2·Δt+mvA2·Δt，

5m·1.2v0·Δt=5mvB3·Δt+mvA3·Δt，

…

累积后可得5m·1.2v0·t0=5mxB+mxA，其中xA和xB分别是物块A 和B对地的位移，而xA=0.36v0t0，解得xB=1.128v0t0，因此弹簧压缩量的最大值Δxmax=xB-xA=0.768v0t0.

解法2：采用微元法结合运动的合成和分解知识.

解法3：利用质心的定义式.

图2

解法5：利用折合质量的思想.