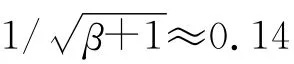漂浮于烧杯液体中的浮体微幅振荡问题
张元元
(广东省中山市中山纪念中学,广东中山 528454)
2022年5月24日第6届欧洲物理奥林匹克竞赛(Eu PHO)刚刚落下帷幕,其理论第1题是一道有关浮体微幅振荡问题.我们常见的浮体是指漂浮于广阔的液体表面的物体,当浮体受到不是太大的扰动时,在液面附近振荡的浮体的上表面始终位于液面之上,忽略浮体运动导致液体的运动,即忽略振荡的液体对浮体运动的影响.本届EuPHO 分析漂浮于烧杯液体中的浮体微幅运动,由于烧杯中液面有限,不能忽略振荡的液体对浮体运动的影响,与此同时,还要进一步判定烧杯中哪部分液体的运动起到主导作用,从而构建模型计算振荡运动的周期.
1 英文原题及中文翻译
A solid,uniform cylinder of heighth=10cm and base areaS1=100cm2floats in a cylindrical beaker of heightH=20cm and inner bottom areaS=102cm2filled with a liquid.The ratio between the density of the cylinder and that of the liquid isγ=0.70.The bottom of the cylinder is above the bottom of the beaker by a few centimeters.The cylinder is oscillating vertically,so that its axis always coincides with that of the beaker.The amplitude of the liquid level oscillations isA=1mm.
Find the period of the motionT.Neglect the viscosity of the liquid.
一高度h=10 cm、横截面积S1=100 cm2的固体均匀圆柱体漂浮在高度H=20 cm、内部横截面积S=102 cm2的圆柱形烧杯里的液体中.圆柱体的密度与液体密度的比值γ=0.70.圆柱体的底部位于烧杯底部上方几厘米处.当圆柱体在垂直方向振荡,其轴线始终与烧杯轴线重合.已知液体振荡的幅度A=1 mm.
试求振荡运动的周期T.忽略液体的粘度.
2 分析系统振荡情形以及构建系统振荡模型
2.1 系统静止时的相关参数
系统静止时的立体图以及侧视图如图1 所示,浮力与重力相平衡,有

图1 系统静止示意图

可知圆柱体浸没液体的深度h0为

由于圆柱体的底部位于烧杯底部上方几厘米处,烧杯的高度H=20 cm,我们可知圆柱体的顶部位于烧杯口部下方几厘米处,液面更低于烧杯口.
2.2 系统微幅振荡时的液面高度变化
当圆柱体在液面附近微幅振荡时,烧杯中液面也在上下微幅振荡.题中并未指明液体是否具有不可压缩性,在缺乏条件下,我们显然将液体视为不可压缩流体,这样我们进一步分析在实验室参考系中,液面高度的变化量为y1.不失一般性,当圆柱体从平衡位置向下移动x时,如图2所示,液体体积不变,有

图2 系统振荡示意图

可知液面高度的变化量y1为

式中参量β=50.液体振荡的幅度A=1mm 是指振荡过程中y1的极大值是1 mm,因此圆柱体偏离平衡位置的最大值xmax=0.02mm,说明系统振荡过程中液体的液面不仅低于圆柱体的顶部,更低于烧杯口,液体振荡时不可能有液体溢出烧杯.
2.3 系统微幅振荡时液体运动情形
系统振荡时,圆柱体上下振荡,液体的振荡情形较为复杂,不仅圆柱体侧面部分液体处于运动状态,圆柱体底部以下部分液体也处于运动状态.由(4)式可知液面向上运动的速度u与圆柱体向下运动的v之间的大小关系,即

圆柱体底部以上部分液体向下运动情形甚为复杂,其运动速度的上限值近似等于圆柱体运动的速度v.假设圆柱体底部以下液体的深度d=5cm,其动能上限值Ekb约为

由于液体具有不可压缩性,圆柱体侧面部分液体向上运动的速度均为u,其动能Ek为

Ekb与Ek的比值为

从结果可以看出Ekb≪Ek,忽略圆柱体底部以下液体运动是合理的,建立振荡模型时,仅考虑圆柱体侧面部分液体的运动.
2.4 系统微幅振荡时圆柱体受到的浮力作用
当圆柱体向下运动的加速度为a时,其侧面部分液体向上运动的加速度a*为

此时圆柱体浸没在液体中的深度y为

圆柱体受到的浮力写成如图3所示的形式是错误的,该浮力公式是针对液体加速度为0 的情形,对圆柱体侧面液体受力分析,有

图3 错误浮力示意图

可知圆柱体底部压强p与液面上方大气压强p0的差值为

圆柱体受到的浮力F为

3 分析微幅振荡运动的周期
3.1 动力学特征方程法
由于圆柱体振荡周期与系统振荡周期是一致的,选择圆柱体作为分析的对象,如图4所示,振荡过程中的动力学方程为
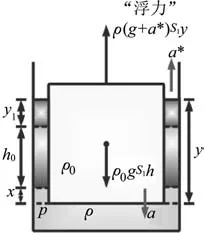
图4 圆柱体受力示意图

由(9)、(10)、(13)、(14)式可得
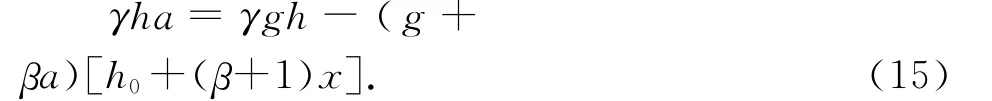
考虑到微幅振荡,x≪1,a≪1,略去二阶小量β(β+1)ax,(15)式简化后符合简谐运动的动力学特征方程,即

因此振荡的周期T为

3.2 能量特征方程法
忽略液体的粘度,系统是一保守系统,当系统振荡时,总的机械能E是恒定的.因此,我们也可以选择系统作为分析的对象,振荡过程中系统的动能Ek可表示为
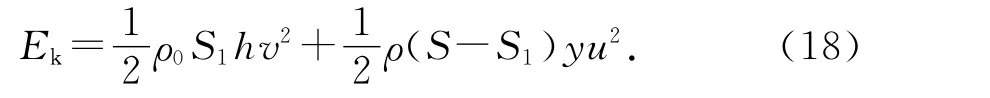
忽略高阶小量(β+1)x,动能Ek为

系统处于平衡位置时,系统的重力势能记为E0.当圆柱体从平衡位置向下运动的距离为x时,液面的高度上升了y1,根据割补法可知液体重力势能的增加量等于横截面积为S1、深度为x的液体势能增大到液体表面处横截面积为S-S1、深度为y1时液体的势能,该部分液体重心升高的高度hC为

考虑到圆柱体重力势能减小,此时系统的重力势能Ep可表示为

最终系统的重力势能Ep为

根据系统机械能守恒条件,即Ek+Ep=E,可知系统的能量方程为

(23)式关于变量x及其一阶导数v的方程符合简谐运动的能量特征方程,振荡周期T为
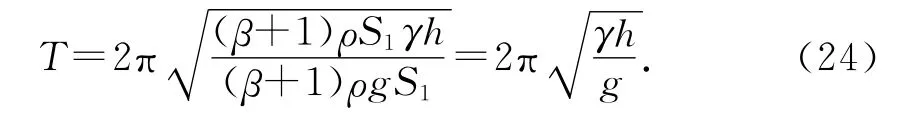
4 总结