圆视角下的动态三角形运动界限
广东省佛山市南海区狮山石门高级中学(528225) 陈基耿
动态三角形的运动变化问题是高考解三角形试题的基本问题,解三角形试题的命制过程和呈现形式,体现了三角形的运动变化过程,或从动态到唯一确定进行解三角形(求边长、角度、面积),或分析动态三角形的运动界限(取值范围或最值).教育部考试中心着力新高考试题改革[1-2],解三角形试题变化尤为深刻.近年全国卷新高考解三角形试题,问题情境新颖,给考生很大的挑战.考生由于未能对三角形进行恰当的构形,在缺乏几何直观的情况下,解答方向不明确,数理运算举步维艰.本文尝试在圆的辅助下,对三角形进行直观构形,分析新高考试题中动态三角形的运动变化规律,还原几类常见问题的命题设计思路,从直观角度探寻问题解答的策略.
一、有一个内角为定角的三角形的运动界限
有一个内角为定角的三角形是最常见的动态三角形模型.内角为定值体现为两种情况: ①内角为特殊角; ②内角的三角函数值为定值.这两种情况均易于在三角形的外接圆中进行构形,从直观上分析三角形的运动变化规律,确定三角形的运动界限.
例1ΔABC的内角A,B,C的对边分别为a,b,c,分析三角形的运动变化情况.
分析任意三角形都有外接圆,同弧所对圆周角等于圆心角的一半.如图1,在圆O内作等边三角形OAB,得圆心角因此圆周角为定值.三角形顶点C为动点,运动界限为圆的优弧

图1
例2ΔABC的内角A,B,C的对边分别为a,b,c,分析三角形的运动变化情况.
分析同弧所对圆周角等于圆心角的一半, 则圆周角等于半圆心角.如图2, 在直角三角形COP中, 点P为AC中点, 半径CO=3CP, 则半圆心角∠COP=B,所以三角形顶点B为动点,运动界限为圆的优弧

图2
借助外接圆中单定角三角形运动模型,易于分析三角形的边长、角、周长以及面积的取值变化界限.以下两道高考试题非常典型,第一问通过运算求解确定一个内角为定角,此时定角所在顶点在圆周上运动,第二问添加条件,确定三角形的运动界限.
真题1(2020年新高考Ⅱ卷第17 题)ΔABC中,sin2A-sin2B-sin2C=sinBsinC,(1)求A;(2)若BC=3,求ΔABC周长的最大值.
真题2(2019年高考新课标Ⅲ卷第18 题)ΔABC中,已知(1)求B; (2)若ΔABC为锐角三角形,且c=1,求ΔABC面积的取值范围.
分析首先求得如图3,在外接圆中构形,顶点B为动点,运动界限为圆的优弧若三角形为锐角三角形,则顶点B的运动界限为劣弧(不包括端点).再添加条件c=1,则BC边上的高为定值,如图4,由面积公式知三角形的面积由底边BC边长唯一确定.B1C和B2C是边长BC运动变化的上下界限.

图3

图4
值得注意的是,“三角形的高”和“一边在另一边的投影”是常见的两种比较隐蔽的条件,受到命题人的青睐.考生若能从直观上识别并构形,如同重构了命题人的“原图”,从命题人的角度分析思考问题,自是豁然开朗,事半功倍.
真题3(2020年新高考I卷第17 题)在②csinA=3,这三个条件中任选一个, 补充在下面问题中,若问题中的三角形存在,求c的值;若问题中的三角形不存在,说明理由.问题: 是否存在ΔABC,它的内角A,B,C的对边分别为a,b,c, 且____?
分析在例题1 的基础上, 由得则三角形的形状被唯一确定, 如图5.此时三角形外接圆半径未定, 则三角形大小未定.因此再选择条件②csinA=3,该条件的几何意义表示边b上的高为3,如图6,因此确定三角形的各边长,实现解三角形.

图5
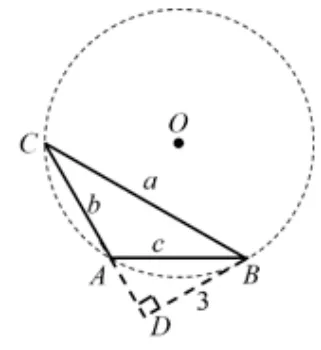
图6
真题4(2019年高考新课标I卷第17 题)ΔABC的内角A,B,C的对边分别为a,b,c, 设(sinB-sinC)2=sin2A-sinBsinC.

(1)求A;形状,实现解三角形.

图8

以上近年几道高考真题,均设计单定角三角形在外接圆中的运动变化模型.真题2 和真题3 均以“三角形的高”约束三角形的运动,实现解三角形.真题4 和真题5 设计的图形背景和思路是完全一致的,均以“边的投影”约束三角形的运动,实现解三角形.
二、与切割线或相交弦相关的三角形的运动界限
三角形两内角和差关系确定的动态三角形问题,可以在圆的辅助下,直观分析三角形的运动界限.三角形两内角和为定值,则第三角为定值,归结为上面第一种情况.三角形两内角差为定值,则三角形的运动变化常关联圆的切割线或相交弦运动变化问题.三角形某边分点处添加辅助线问题,则显式关联圆的相交弦问题.
例3ΔABC的内角A,B,C的对边分别为a,b,c,分析三角形的运动变化情况.
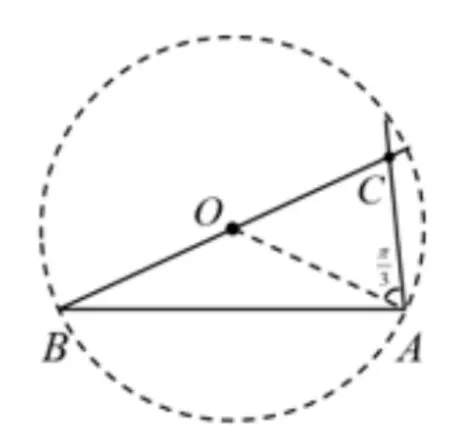
图9
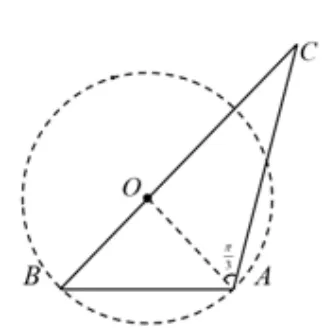
图10



图11
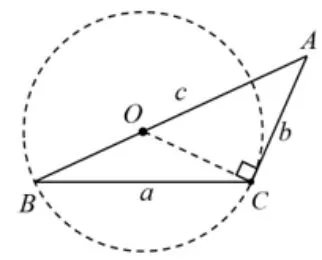
图12

后续,易于从函数导数或基本不等式的角度,分析该函数的最小值.

图13
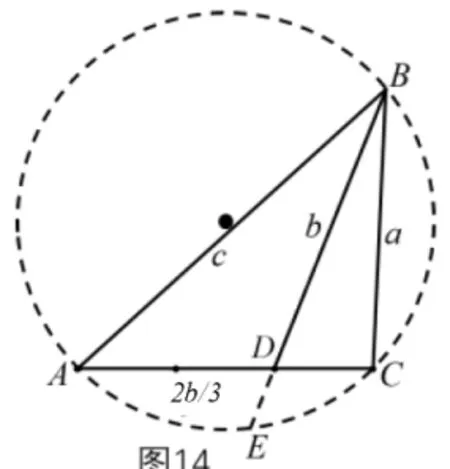
图14
真题7(2021年新高考I卷第19 题)记ΔABC的内角A,B,C的对边分别为a,b,c.已知b2=ac, 点D在边AC上,BDsin ∠ABC=asinC.(1)证明:BD=b; (2)若AD=2DC,求cos ∠ABC.
分析易于证得BD=b,结合AD=2DC,AC与BD为圆内的两条相交弦.根据相交弦定理(或相似三角形),有AD·CD=BD·ED,所以确定该三角形的构造背景为圆内的相交弦问题,两段弦长度关系确定,固定分点相交.直观上,两相交弦夹角的变化决定了ΔABC的运动变化,同时边a,c跟随变化.添加条件b2=ac,将约束相交弦的运动,也就约束了三角形的运动,确定三角形的形状,实现解三角形.
三角形运动变化的“因”,自然是解答问题的突破口.设∠ADB=θ,在ΔADB中,在ΔCDB中,两式 消 去cosθ, 得结 合b2=ac, 得6a2-11ac+3c2=(2a-3c)(3a-c)=0.后续易于解三角形.该题在外接圆的辅助下,也可延续从相交弦角度进行进一步分析,解答过程将更直观[3].
真题6 和真题7,在圆的辅助下对三角形进行构形,易于从直观上明确三角形运动变化的“因”,也就发现了问题解答的突破口.直观上明确解答问题的方向,数量上求解三角形的“界”.本文对解三角形试题的研究,充分体现圆视角下构形的优越性,还原命题设计思路,直观探寻问题解答策略.

