多思维切入 多方法应用*——以2022年新高考Ⅱ卷第12题为例

江苏省天一中学(214101)安恺凯

无锡市东北塘中学(214101) 沈丹丹

双变量范围问题一直是各类考试中的热门问题,这类问题知识层面广泛、思维视角发散、方法应用多样,即常涉及不等式、函数、方程等高中重点知识,又常涉及矩阵变换、偏导数、二次曲线的一般理论等高等数学知识.符合新高考突出考查关键能力、深入考查思维品质、加强试题选拔功能的命题导向,因此在新高考中亦然深受命题人青睐,2022年新高考Ⅱ卷的多选压轴题便是一个例证.对其解题思路与方法进行多角度的探究,有利于创新思维、开阔视野、加深理解,更好发挥新高考真题对日常解题教学的指导性.

1 试题呈现

试题(2022年全国新高考Ⅱ卷第12 题)若x,y满足x2+y2-xy=1,则( )

A.x+y≤1 B.x+y≥-2 C.x2+y2≤2 D.x2+y2≥1

2 思维方法

2.1 思维视角一 不等式思维

评注基本不等式是高中阶段得到和、积、平方和之间不等量关系的基本路径.只要教师在平时的教学活动中确切立足于四基,即引导学生理解基础知识、习得基本技能、感悟基本思想、积累基本活动经验,学生便不难由此路径获得结果.

解法2(配方法)由x2+y2-xy=1,得

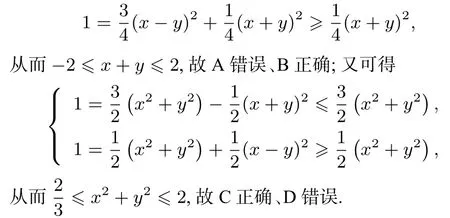
评注配方法处理主要是根据题目中代数式的结构特征,从不同视角来合理配方,再根据需求的代数式范围来确定放缩部分.对于用配方法求选项A、B 中一次式x+y的范围,须先将x+y通过平方转化为二次式,笔者在下面方法3中针对x+y给出另外一种转化为二次式的方法.

解法3(0 的妙用)由x2+y2-xy-1=0,可得

又可得

故A 错误、B 正确.

评注方法3 分别通过巧加0 和巧减0,将一次式“x+y”有效转为二次式,继而配方求得最值.

2.2 思维视角二 换元思维

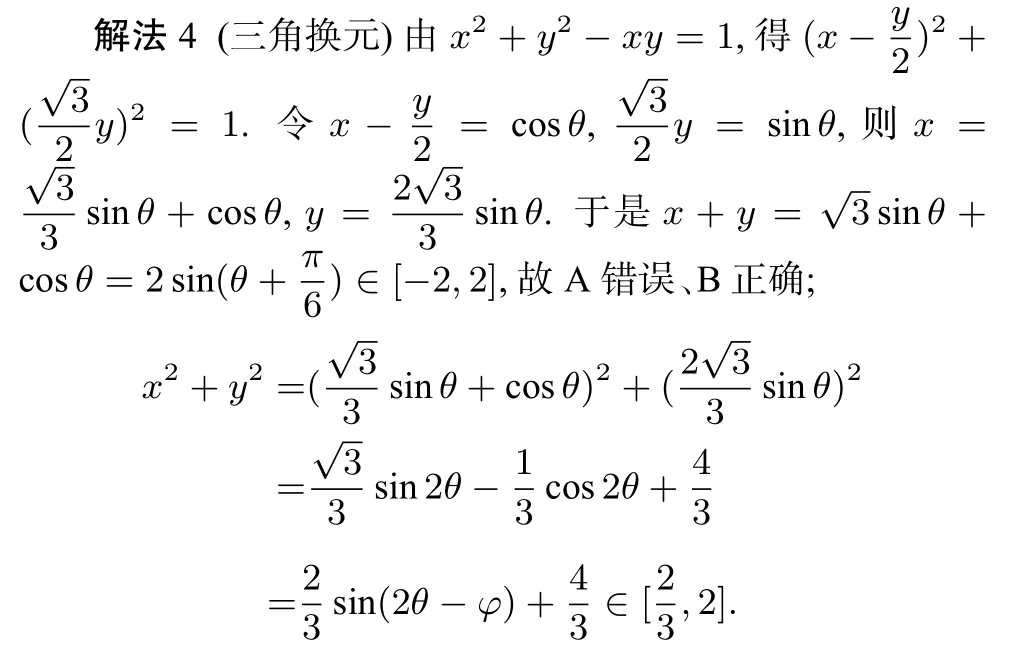
故C 正确、D 错误.

评注三角换元法首先结合题目条件中的关系式进行合理配方,使得对应的数式恒等1,从而引入三角函数,进行三角换元,继而合理的三角恒等变形以及三角函数性质的应用是解题关键.三角换元法是处理一些具有明显特征的双变量范围问题(这里两数之和为1)时比较常用的一种技巧方法.

解法5(和差换元)令x=a - b,y=a - b, 则x2+y2- xy=a2+3b2=1, 从而a ∈[-1,1],b ∈于是x+y=2a ∈[-2,2], 故A 错误、B 正确;x2+y2=2a2+2b2=2-4b2∈,故C 正确、D 错误.

评注和差换元法可以有效相除xy项,相当于坐标轴旋转.

从而x+y ∈[-2,2],故A 错误、B 正确;

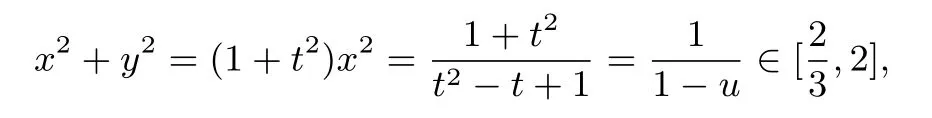
故C 正确、D 错误.

评注比值换元法结合线性换元引入参数,可以有效地将双变量问题转化为单变量问题,继而转化为对应的函数关系式,进而巧妙利用相应的函数单调性来分析与处理.

2.3 思维视角三 方程思维

解法7(判别式法)记x+y=m,x2+y2=n.若方程组有解,等价于方程3x2-3mx+m2-1=0 的判别式Δ=9m2-12(m2-1)≥0, 解得-2 ≤m≤2,故A 错误、B 正确;由于

亦等价于n≥2|n-1|,解得故C 正确、D 错误.

评注通过所求代数关系式的整体化处理,引入参数.对于A、B 选项,代入条件中的关系式进行合理消元,转化为关于x的方程,再结合方程有解的前提条件,通过判别式的构建来确定参数m的取值情况;对于C、D 选项,则用参数n分别表示双变量的平方和与积,再结合基本不等式,来确定参数n的取值情况.

2.4 思维视角四 坐标变换思维

解法8(极坐标变换)故C 正确、D 错误;又因为

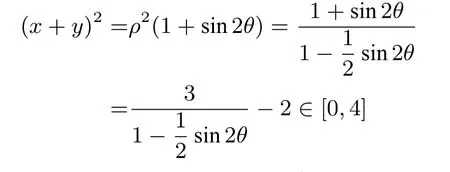
所以x+y ∈[-2,2],故A 错误、B 正确.

评注在极坐标下,二次曲线上点的坐标(ρ,θ)所满足的条件更容易表示,代数变化也更加直接.

解法9(矩阵旋转变换)考虑如下的变换(其几何意义是将坐标轴旋转):

评注通过旋转变换化简二次曲线是数学专业大一的解析几何课程教学内容之一,有兴趣的读者可参看相关教科书了解更多的细节.

2.5 思维视角五 高观点思维

解法10( 拉格朗日乘数法)记f(x,y)=x+y, 构造L(x,y,λ)=x+y+λ(x2+y2-xy-1).令

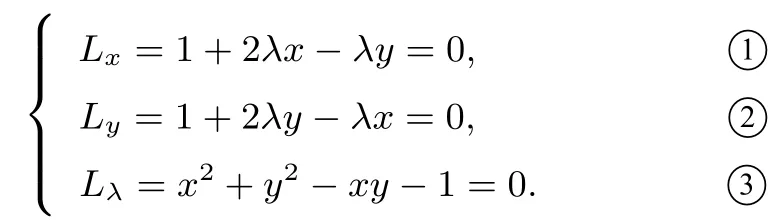
由①②可得x=y,代入③解得x=y=1 或x=y=-1.所以当x=y=1 时,f(x,y)取得最大值2;当x=y=-1时,f(x,y)取得最小值-2.故A 错误、B 正确.记g(x,y)=x2+y2,构造L′(x,y,λ)=x2+y2+λ(x2+y2-xy-1).

令

评注拉格朗日乘数法可以有效将约束条件x2+y2-xy=1 融入目标函数中,即将关于双变量(x,y)的条件最值问题转化为关于三变量(x,y,λ)的无条件最值问题,继而令偏导数为0 求得的点称为稳定点.对于数学素养较高、创新意识较好的学生,基于导数知识体系,来理解偏导数并非难事.若要继续判断稳定点是否为极大(小)值点,需要验证二阶偏导数组成的Hesse 矩阵在稳定点处的正定性,不适宜再向高中生推广,但这并不影响学生通过对全部稳定点处的函数值进行大小比较来求得最值.

解法11(不变量法)文献[1]指出,一般地,由二元二次方程Γ:Ax2+2Bxy+Cx2+2Dx+2Ey+F=0(A,B,C不能全为0)所表示的图形称为二次曲线,称

为Γ 的不变量.借助于不变量,可对Γ 进行如下分类:

①若I2＞0 且I1I3＜0,则Γ 为椭圆;

②若I2＜0 且I3≠0,则Γ 为双曲线;

③若I2=0 且I3≠0,则Γ 为抛物线.

解析对于二次曲线Γ:F(x,y)=x2-xy+y2-1=0,有因为I2＞0 且I1I3＜0, 所以Γ 为椭圆.由F(x,y)=F(-x,-y), 可得Γ 关于原点对称; 由F(x,y)=F(y,x), 可得Γ 关于y=x对称; 由F(x,y)=F(-y,-x), 可得Γ 关于y=-x对称.进而联立椭圆Γ 与对称轴方程, 可得椭圆的四个顶点分别为A(1,1),B(-1,-1),

由此可得, 如图1, 当直线y=-x+b与Γ 有公共点时,-2 ≤b≤ 2, 即-2 ≤x+y≤2, 故A 错误、B 正确.

图1

设Γ 上任意一点到原点距离为d, 则有即故C 正确、D 错误.

评注二次曲线方程在高等数学范畴内的不变量法给出了曲线类型的清晰明确的判断方式,但与高中解析几何知识体系相距较远,故不宜向学生介绍.然而,若教师在平时教学中确切做到由“知识立意”向“能力立意”转变,学生由此养成较好的独立思考能力,便不难通过二次曲线Γ 关于原点、直线y=x、y=-x对称的几何特征,以及二次曲线Γ 与对称轴的交点画出图像,继而由数形结合“秒杀”本题.

3 结束语

2022年新高考数学试卷学生普遍反馈颇有难度,反映出学生对新高考命题思路和考试方位的不适应性.新高考更注重对思维品质的考查,强调独立思考和创新意识;更加注重对关键能力的考查,强调发挥数学学科的选拔功能.在解题教学过程中,注重培养学生对一类问题多思维剖析,注重寻找一类问题的多种解法,能有效培养学生思维的创新型和发散性,能有效提高学生独立思考能力和深度思考能力,从而帮助学生更好适应新高考带来的变化.