例谈非对称极值点偏移问题

深圳市龙华区教育科学研究院附属外国语学校(518109) 钟文体

一、从极值点偏移问题谈起

已知函数f(x),设x1和x2是两个不相等的实数且满足f(x1)=f(x2),要求证明形如x1+x2＞m或x1+x2＜m的不等式.这类问题通常称为极值点偏移问题.极值点偏移问题近年来屡次出现在各地高考和模考试题中,是函数压轴题的一种重要类型.例如,2021年新高考I卷第22 题就是一道典型的极值点偏移问题.此类问题思维难度大,对分析和推理能力有较高的要求, 考察函数与导数知识的综合运用,涉及函数与方程,转化与化归等重要数学思想方法.专家和一线教师对极值点偏移问题作了大量研究,在中国知网可以检索到二百余篇关于这一主题的文献.经过大量的解题研究和长期的教学实践,此类问题已形成成熟的处理策略.常见的解题策略主要有以下三种: 构造对称差函数,齐次化方法,利用对数均值不等式[1-4].

不妨称上述极值点偏移问题为对称极值点偏移问题.与近年来对称极值点偏移问题的“火爆”形成鲜明对比的是非对称极值点偏移问题的“冷清”.先阐释何谓非对称极值点偏移问题.

已知函数f(x)和两个不相等的非零实数a和b.设x1和x2是两个不相等的实数且满足f(x1)=f(x2),要求证明形如ax1+bx2＞m或ax1+bx2＜m的不等式.

我们称这类问题为非对称极值点偏移问题.就笔者所知,似乎还没有相关文献专门研究非对称极值点偏移问题.为了弥补这一遗憾,笔者不揣浅陋,以例为纲,浅谈此类问题的解决方法,以期抛砖引玉.

二、非对称极值点偏移问题初探

我们以2021年新高考I卷第22 题的函数f(x)=x(1-lnx)为研究对象, 呈现非对称极值点偏移问题的一些解决方法.

问题(2021年新高考I卷第22 题改编)已知函数f(x)=x(1-lnx).设s ＜t且f(s)=f(t), 我们希望研究表达式s+λt的取值范围.

易知f′(x)=-lnx,于是f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,fmax=f(1)=1,其图象如图1 所示.由图象可知0＜s ＜1,1＜t ＜e 且s和t的单调性相反,即当s增大时,t减小;当s减小时,t增大.于是,当λ ＜0 时,s+λt随s的增大而增大,从而s+λt ＞λe(当s →0 时),s+λt ＜1+λ(当s →1 时).下面探究λ ＞0 的情形.

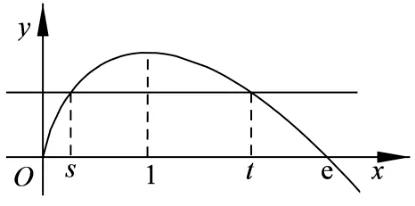
图1

1.证明3＜s+2t ＜2e.

为了降低问题的复杂度,我们先从λ=2 这一较简单的情形开始.

注不等式3＜s+2t ＜2e 是如何想到的? 让s →1,则由图1 可知t →1, 从而s+2t →3.再让s →0, 则由图1 可知t →e,从而s+2t →2e.于是,可以合理地猜测不等式3＜s+2t ＜2e 成立.2021年新高考I卷原题等价于证明2＜s+t ＜e,若已知这一结论,则很容易证明待证不等式.事实上,s+2t=(s+t)+t ＞2+t ＞2+1=3,s+2t=(s+t)+t ＜e+e=2e.若不使用中间结论2＜s+t ＜e,可用如下方法证明.

首先s+2t ＞3⇔s ＞3-2t,因3-2t ＞且3-2t ＜3-2×1=1,即3-2t ∈(0,1),又因f(x)在区间(0,1)上单调递增,故s+2t ＞3⇔s ＞3-2t ⇔f(s)＞f(3-2t).

注意到f(s)=f(t),故s+2t ＞3⇔f(t)＞f(3-2t).构造函数g(x)=f(x)-f(3-2x),, 只需证明g(x)＞0 即可.求导得

评注上述方法的思路源于求解对称极值点偏移问题的对称差函数方法,将关于s和t的双变量不等式问题转化为关于t的单变量不等式问题.实际上,也可以转化为关于s的单变量不等式问题,此时“充要条件链”为

具体细节留给读者.我们再用类似的思路证明不等式右边.

评注用类似的方法可以证明当λ ＞1 时, 1+λ ＜s+λt ＜λe.当然,也可以用已知结论2＜s+t ＜e 进行证明.下面探究λ ＜1 的情形.

评注条件似乎有点突兀,但它实际上是不等式λe ≤1+λ的解集.

因1+λ - λt ＞1+λ - λe=1- λ(e-1)≥且1+λ - λt ＜1+λ - λ=1,即1+λ-λt ∈(0,1),于是,根据f(x)在区间(0,1)上单调递增且f(s)=f(t),有如下“充要条件链”:

构造函数g(x)=f(x)-f(1+λ-λx),x ∈(1,e),只需证明g(x)＜0 即可.求导得

令h(x)=x(1+λ-λx)λ,求导得

h′(x)=(1+λ)(1+λ-λx)λ-1(1-λx),

评注让s →1,则t →1,故s+λt →1+λ,从而上界1+λ是最优的.我们自然会问,此时λe 是s+λt的下界吗? 即s+λt ＞λe 成立吗? 应用绘图软件GeoGebra 可知这并不成立.例如,取λ=0.5,用GeoGebra 求得函数f(x)=x(1-lnx)的图象与直线y=0.4 的两个交点的横坐标约为0.13 和2.28,故0.13+0.5×2.28=1.27＜0.5e≈1.36.

评注用已知结论2＜s+t ＜e 可以证明当λ ＞1 时,s+λt ＜λe 成立,但这种方法不能应用到λ ＜1 的情形,需要单独证明.

因k(0)=λe＞0,于是可分为以下两种情形讨论.

(1)若存在x′ ∈(0,1)使得k(x′)=0,则当x ∈(0,x′)时,k(x)＞0,h′(x)＞0,h(x)单调递增; 当x ∈(x′,1)时,k(x)＜0,h′(x)＜0,h(x)单调递减.因h(0)=0,故存在x0∈(0,x′)使得h(x0)=1.当x ∈(0,x0)时,h(x)＜1,g′(x)＞0,g(x)单调递增; 当x ∈(x0,1)时,h(x)＞1,g′(x)＜0,g(x)单调递减.又因从而g(x)＞0.于是待证不等式成立.

(2)若k(x)在(0,1)上恒大于零, 则h(x)在(0,1)上单调递增.因h(0)=0,h(1)=＞e-(e-1)=1,故存在x0∈(0,1)使得h(x0)=1.当x ∈(0,x0)时,h(x)＜1,g′(x)＞0,g(x)单调递增; 当x ∈(x0,1)时,h(x)＞1,g′(x)＜0,g(x)单调递减.又因从而g(x)＞0.于是待证不等式成立.

评注让s →0,则t →e,因此s+λt →λe,故上界λe是最优的.同样会问,当时,s+λt ＞λ+1成立吗? 应用绘图软件GeoGebra 可知这并不成立.例如,取λ=0.6,前面已经知道函数f(x)=x(1-lnx)的图象与直线y=0.4 的两个交点的横坐标约为0.13 和2.28, 故0.13+0.6×2.28=1.498＜1+0.6.

评注当λ ＜1 时如何找下界是一个比较困难的问题,一般情形留给感兴趣的读者进一步探究.

5.齐次化方法

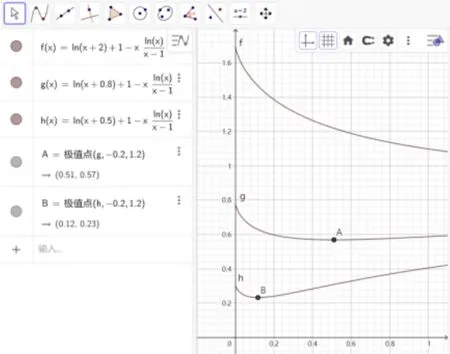
图2

三、更多的例子

上面呈现的方法具有一定的普适性,可以用类似的方法解决其它非对称极值点偏移问题,下面再举一些典型的例子.

类题2已知函数f(x)=ex - x.设s ＜ t且f(s)=f(t),证明s+2t ＜ln 2.

证明由f′(x)=ex-1 可知f(x)在区间(-∞,0)上单调递减, 在区间(0,+∞)上单调递增, 从而s ＜0,t ＞0.

通过上面的几个例子可以看到,本文的方法可以处理常见的非对称极值点偏移问题,求解思路很清晰,是一种可行的解题策略.当然,也许还有更好的方法,期待未来有更多的文献探讨这一问题.