载重车辆-伸缩缝耦合系统的垂向振动数值模拟方法

张 露 ，李 冰 ，王少华 ，李怀仙

（1. 西南交通大学机械工程学院， 四川 成都 610031；2. 西南交通大学轨道交通运维技术与装备四川省重点实验室，四川 成都 610031；3. 华北水利水电大学机械学院，河南 郑州 450045）

大型桥梁上使用的大位移伸缩缝属于定制产品. 受研发成本的限制，目前大位移伸缩缝的设计和检验均以静态性能指标为依据，对产品动态性能的试验研究应用较少，产品性能无法满足国内桥梁重载和大车流量的需求，使用寿命大幅缩减[1]. 同时由于缺乏大位移伸缩缝动态特性的研究和高效、精确的计算方法，现有的动态监测数据多用于滑动部件的磨损预测和位移监测[2-3]，基于振动特性的故障监测难于实现. 因此，急需对大位移伸缩缝动态特性数值模拟方法展开研究.

目前，国内外学者的研究多把大位移伸缩缝作为单独的系统进行研究，研究中使用正弦荷载模拟车辆载荷代替车辆的作用，分析了车速、缝宽、弹性元件刚度等参数对伸缩缝性能的影响规律[4-6]. 这类方法只适用于研究伸缩缝的振动规律，由于缺少车辆模型，往往不能准确地反映车辆荷载的冲击效应[7]. 因此，车辆与大位移伸缩缝的耦合作用问题值得考虑.

Sun 等[8]采用轮胎点接触模型建立一种考虑车辆作用的大位移伸缩缝实体单元有限元模型，分析了车速影响下大位移伸缩缝的振动特性，研究结果表明车辆荷载会引起大位移伸缩缝的显著动力响应. Friedl 等[9-11]提出了一种基于印迹恒定的平面弹簧轮胎模型，并基于该模型建立了车辆与大位移伸缩缝耦合系统的动力学方程，研究了车速和横梁位置对大位移伸缩缝垂向振动冲击系数的影响，但由于轮胎模型过于简单，需要考虑对轮胎力的修正问题. 丁勇等[12-13]提出了一种基于分布弹簧阻尼单元的车-桥-伸缩缝耦合系统动力学模型建模方法，模型中采用迭代方法求解轮胎的动态印迹长度，对车辆和桥梁的动态响应分析结果表明车辆轴载和桥梁内力的冲击效应高于我国现行桥梁规范的建议值. 吴延平等[14]基于刚性车轮建立了车辆-简支钢箱梁数值模型，验证了伸缩缝的存在会显著增大车辆的冲击效应. 以上的研究结果表明了车辆对伸缩缝有明显的冲击效应. 研究中有限元模型仿真求解方法精度高，但对计算资源的需要过高、计算效率低、难于推广. 数值模型求解速度快，但恒定印迹假设会造成耦合系统中轮胎力的冲击过大，迭代求解动态印迹的方法求解又效率偏低、且采用的轮胎力传递模型没有轮胎的刚性位移对印迹长度的影响，因此，需要对车辆-大位移伸缩缝耦合系统寻求更加细致化合理的方法.

本文以ZL1600 模数式大位移伸缩缝为研究对象，首先在分析轮胎载重车辆-伸缩缝耦合系统受力特点的基础上提出了一种考虑轮胎力真实激励特性的耦合动力学数值模型，并采用新型积分算法对数值模型进行求解，然后进行了轮胎载重车辆-伸缩缝耦合系统动态试验测试，通过仿真结果与试验测试结果对比验证动力学模型的有效性，最后分析了车辆对伸缩缝的冲击效应，为耦合系统性能的进一步研究提供基础.

1 车辆-大位移伸缩缝耦合系统垂向动力学模型

ZL1600 模数式大位移伸缩缝主要由边梁、中梁、横梁、中梁支承组件、横梁支承组件、位移箱锚固系统和防水密封条等组成. 车辆选用国产某型四轴轮胎载重车辆为计算实例. 车辆通过车轮与伸缩缝中梁顶面接触，中梁通过中梁弹性元件将垂向荷载传递给横梁，横梁通过横梁弹性元件将垂向荷载传递给桥梁梁体，耦合系统受力如图1 所示. 图中：F011、F021分别为梁体对第1 号横梁1 端和2 端的支反力；FHji为j号横梁对i号中梁的支反力；FIij为i号中梁对j号横梁的支反力；FTki为第k轴车轮作用于i号中梁的垂向载荷；kS1、cS1分别为1 轴悬架刚度和阻尼；kS2、cS2分别为后悬架刚度和阻尼；mC为车体质量；l1、l2、l3分别为1 轴、2 轴和后悬架中心至车体质心的距离；yH、yZ、yT、yC分别为横梁、中梁、轮胎轮心和车体质心的垂向位移；zC为车体质心的水平向位移；v为速度.

图1 车辆-伸缩缝耦合系统受力分析Fig. 1 Force analysis of the vehicle-expansion joint coupled system

1.1 车辆振动微分方程

四轴轮胎载重车辆采用十一自由度整车模型[15]，其中车体具有3 个自由度（垂向振动、侧滚运动和俯仰运动）. 每个平衡悬架具有2 个自由度（垂向振动和俯仰运动）. 前轴左、右车轮分别具有一个垂向振动自由度. 采用D’Alembert 原理建立车辆振动微分方程为

式中：MV、CV、KV分别为四轴车辆的质量矩阵、阻尼矩阵和刚度矩阵[15]；AV、VV、XV分别为四轴车辆的加速度矢量、速度矢量和位移矢量；RV为车辆垂向轮胎力矢量.

1.2 伸缩缝振动微分方程

大位移伸缩缝的中梁、横梁、中梁弹性元件、横梁弹性元件和剪切弹簧为重要的传力部件. 由于伸缩缝的剪切弹簧对伸缩缝的垂向振动特性影响很小[4]，因此以下的研究内容均忽略剪切弹簧. 大位移伸缩缝主要的结构参数如表1 所示.

表1 大位移伸缩缝主要结构参数Tab. 1 Main structural parameters of large displacement expansion joint

i号中梁（i= 1 ～NI，NI为中梁的根数）的振动位移变量为yZi(x,t) ，则其振动微分方程为

式中：EZ为中梁的弹性模量，下标Z、H 分别表示中梁和横梁；t为时间；δ（·）为Dirac 函数；FTLki、FTRki为第k轴左、右侧车轮作用于i号中梁的垂向载荷；NJ为横梁的根数；NK为车轴的根数；xj为j号横梁中心轴的横向坐标；xLk、xRk为第k根车轴左、右车轮的横向坐标.

中梁与横梁通过弹性元件连接，j号横梁对i号中梁的支反力为

式中：k1为中梁弹性元件的刚度；c1为中梁弹性元件的阻尼；yHj(zi,t) 为j号横梁在坐标zi处的振动位移；yZi(xi,t) 为i号中梁在坐标xi处的振动位移；zi为i号中梁中心轴的纵向坐标.

同理，可得j号横梁（j=1～NJ）振动位移量为yHj(z,t)，振动微分方程为

式中：EH为横梁的弹性模量；h为横梁端部弹性元件编号；z0h为h端横梁弹性元件的纵向坐标.

第i号中梁对第j号横梁的支反力为

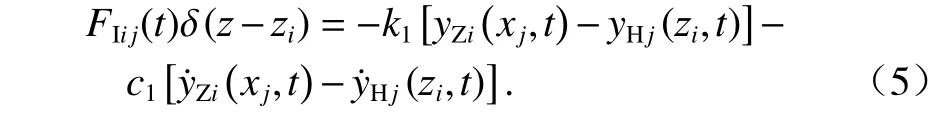
横梁与桥梁梁体通过横梁弹性元件连接，梁体对第j号横梁h端的支反力为

式中：k2为横梁弹性元件的刚度；c2为横梁弹性元件的阻尼.

采用Ritz 法[16]，引入中梁和横梁正则振型坐标qZie(t)和qHjf(t)，式（2）和式（4）的解为

根据模态正交性和Dirac 函数的性质，式（2）两边同时乘以YZie(x)后沿中梁长度L1取积分得

同理，式（4）两边同时乘以YHjf(z)后，沿横梁长 度LH取积分得

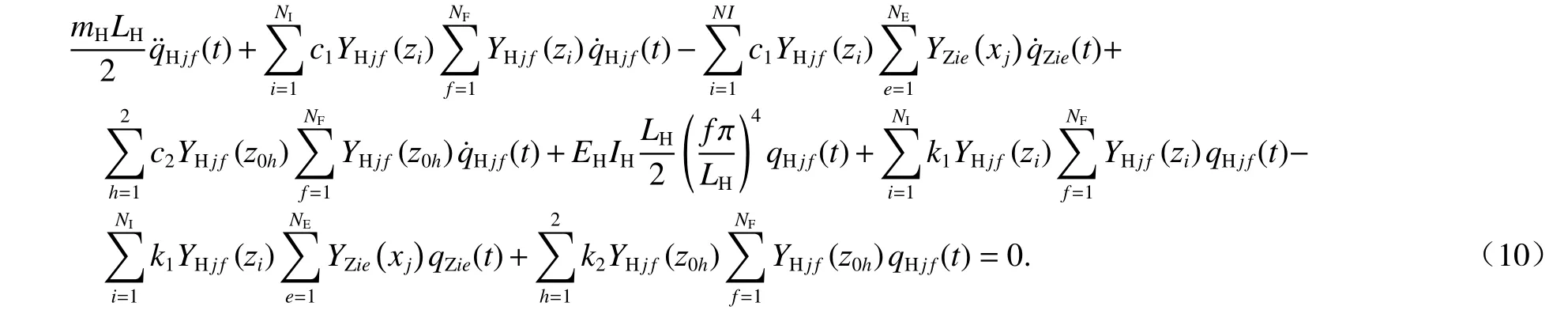
1.3 轮胎与中梁的接触关系

大位移伸缩缝的中梁垂直于路面中轴线布置，因此，轮胎与中梁的接触面具有非连续性的特点，需考虑轮胎印迹范围内局部脱空的情况. 为了准确地表达轮胎与中梁的接触关系，轮胎模型在弹性滚子模型[17-18]中加入了伸缩缝中梁顶面轮廓函数，轮胎与中梁接触关系如图2 所示，图中：y0(ZTk+ZAk) 为伸缩缝中梁顶面轮廓函数，ZTk为第k号轮胎轮心在总体坐标系中的纵向坐标，ZTk=vt，ZAk为第k号轮胎接触印内的局部纵向坐标，-r0≤ZAk≤r0，r0为轮胎自由半径.

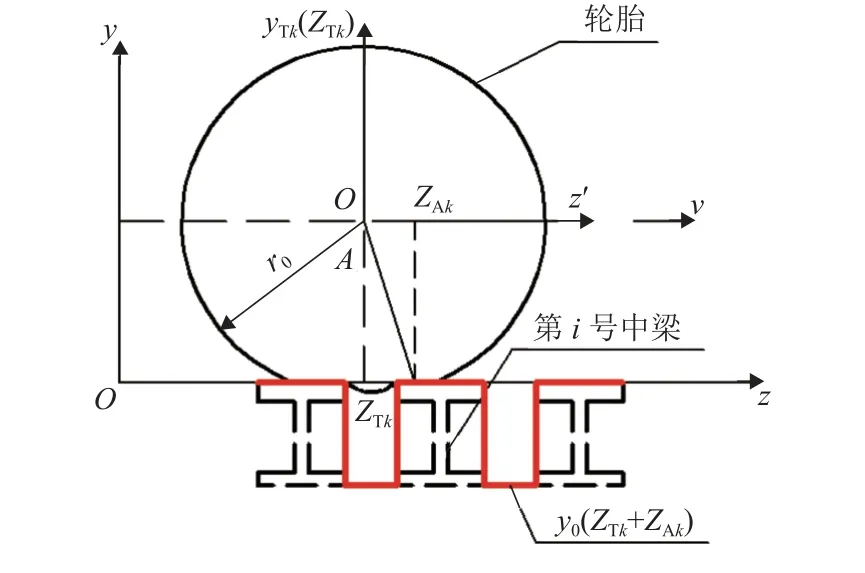
图2 轮胎与中梁接触关系Fig. 2 The contact relationship between the center beam and tire

弹性滚子模型考虑了轮胎的包容性[17]（即几何滤波和弹性滤波特性）、轮胎轴心振动和路面振动条件，能较好地模拟轮胎过缝的过程. 模型中第k号轮胎与伸缩缝第i号中梁各接触点的压缩量为

式中：yTks为车辆静止时第k号车轮的下压量，yTks=-GTk/kTks，GTk为第k号轮胎分配的车辆重力，kTks为第k号轮胎静垂直刚度.

根据伸缩缝中梁顶面的非连续性特点，y0(ZTk+ZAk)表示为

式中：BZ、HZ分别为中梁顶面宽度和中梁高度；BF为缝宽.

第k号轮胎与伸缩缝中梁之间的垂向轮胎合力为

式中：FTki(t)为k号轮胎作用于i号中梁的轮胎力，如式（14）.

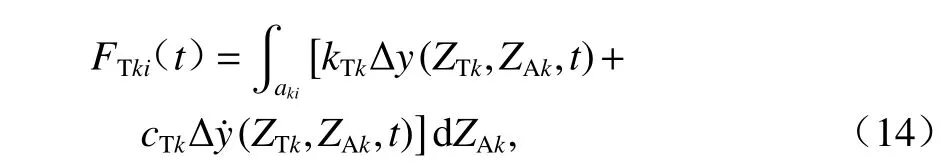
式中：kTk为轮胎垂直分布刚度；cTk为轮胎垂直分布阻尼；aki为第k号轮胎与伸缩缝第i号中梁的接触印迹长度.

由于轮胎的分布垂直刚度、阻尼测定较为困难，因此计算时采用简化公式[17]，轮胎的分布垂直刚度kT、阻尼cT为

式中：kTs、cTs分别为轮胎静垂直刚度、阻尼；ak为轮胎与接触面的接触印迹半长度，如式（16）.

式中：fa为轮胎在荷载作用下的胎面位移.

子午线轮胎在荷载作用下变形时存在带束层刚性位移现象[19-20]. 带束层刚性位移即滚动轴心偏离原轮胎中心的距离为fb，则轮胎在荷载作用下的下沉量ΔyA为

式中：r为轮胎滚动半径.

联立式（1）、（9）、（10）、（11）、（12）得到车辆-伸缩缝耦合系统的运动微分方程组. 采用求解效率高、稳定性好的新型快速积分法[16]，在MATLAB 软件中编制计算程序求解方程组.

2 动力学模型验证

为了得到测试结果来验证耦合系统数值模型仿真结果的有效性，对ZL1600 大位移伸缩缝展开了试验测试.

2.1 试验测试介绍

在成都某公司试验场完成试验. 大位移伸缩缝缝宽B为40 mm. 车辆选用国产某型四轴轮胎载重车辆，车辆参数见表2 所示. 伸缩缝由6 根横梁（H1～H6）和19 根中梁（Z1～Z19）组成. 在实际应用中，载重车辆一般行走于外侧货车道，因此试验中车辆右前轮从伸缩缝第5 根横梁上方位置驶过. 在Z1、Z10、Z13、Z19 号中梁位于H5、H6 号横梁和H4、H5 号横梁跨中处分别布置A、B 两组速度传感器，如图3 所示. 传感器频率范围10～1 000 Hz，灵敏度30 mV/(mm·s-1).

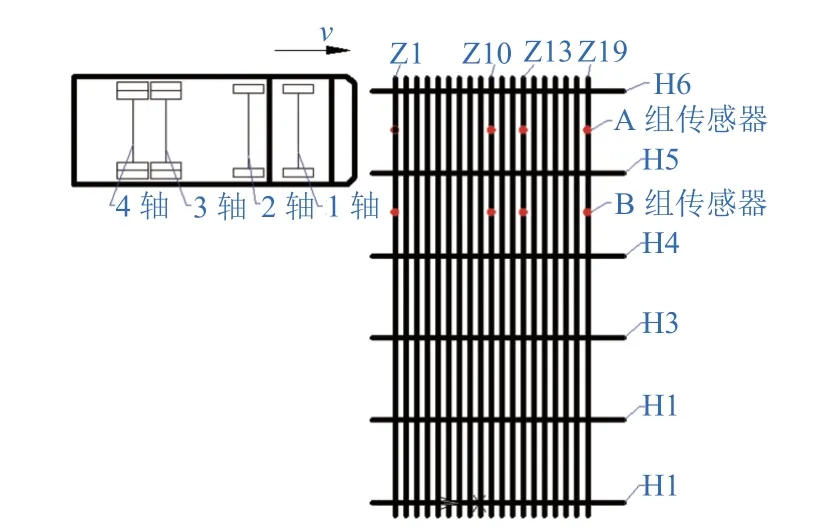
图3 传感器布置Fig. 3 Layout of the sensors

表2 四轴载重车辆动力学参数Tab. 2 Dynamic parameters of four-axle vehicle

2.2 伸缩缝中梁的动态响应验证

图4 为车辆以30 km/h 时车速驶过伸缩缝时Z1 号中梁A 组测点的速度时程曲线对比结果. 由图可知，仿真曲线与试验测试曲线振动趋势基本一致. 由于试验测试时实际车速低于试验设计车速30 km/h，因此，试验测试曲线中轮胎作用在1 号中梁的时间较仿真曲线有滞后.

图4 1 号中梁A 组测点的速度时程曲线（v = 30 km/h）Fig. 4 Speed time history curves of group A measuring points of No.1 middle beam（v = 30 km/h）

图5 为车辆以不同车速通过伸缩缝时Z1 号中梁A 组测点振动速度最大值对比结果. 由图可知：同一车速下1 轴和4 轴分别通过Z1 号中梁时测点的振动速度最大值仿真结果与试验测试结果基本一致，测点的振动速度最大值随速度的变化趋势也一致.

图5 1 号中梁A 组测点振动速度最大值对比Fig. 5 Comparison results of maximum speed at group A measuring points of No.1 middle beam

对中梁测点的速度时程曲线进行积分[21]，可以得到测点的位移时程曲线. 试验测试和仿真计算分别得到车辆以不同车速通过伸缩缝时Z1、Z10、Z13、Z19 号中梁测点最大下沉量对比结果见表3.由表可知：同一车速下各中梁A 组、B 组测点的最大下沉量仿真结果与试验测试结果最大偏差分别为7.8%、8.7%.

表3 中梁测点最大下沉量对比结果Tab. 3 Comparison results of maximum sinking displacement of center beam test points

3 车辆对伸缩缝的冲击效应分析

用冲击系数μ来表示车辆轮胎力对伸缩缝冲击效应的大小，如式（18）.

式中：FTmax为轮胎动态力最大值；FTs为静轮胎力.

图6 为车辆以80 km/h 驶过伸缩缝各中梁（Z1～Z19）及上桥（B2）时车辆轮胎力冲击系数. 由图可知：车辆驶过伸缩缝各中梁时，1、2 轴轮胎力冲击系数小于3、4 轴；车轮驶过伸缩缝上桥时轮胎力冲击系数最大，此处边梁与桥梁梁体端部连接处混凝土最容易发生破坏，与实际应用中梁体端部混凝土病害高发的情况一致.

图6 车辆驶过伸缩缝时轮胎力冲击系数（v = 80 km/h）Fig. 6 Impact factors of tire force when vehicle passing through expansion joint （v = 80 km/h）

图7 为车辆驶上伸缩缝时轮胎力最大冲击系数随车速变化的关系. 由图可知：车辆驶上伸缩缝时各轴轮胎力最大冲击系数随着车速的增大而增大，且3、4 轴轮胎力最大冲击系数增速高于1、2 轴；当车速为120 km/h 时，1、2 轴轮胎力的冲击系数最大值均为0.31，小于我国现行规范[21]的推荐值0.45，3、4 轴轮胎力的冲击系数最大值分别为0.62、0.67，均大于规范[21]的推荐值0.45.

图7 车辆驶上伸缩缝时的最大冲击系数与车速的关系Fig. 7 Relationships between maximum impact factor and speed when vehicle getting on the expansion joint

图8 为车辆驶过伸缩缝上桥时轮胎力最大冲击系数随车速变化的关系. 由图可知：车辆上桥时各轴轮胎力最大冲击系数随着车速的增大而增大；当车

图8 车辆驶上桥梁时的最大冲击系数与车速的关系Fig. 8 Relationship between maximum impact factor and speed when vehicle getting on the bridge

速为120 km/h 时，轮胎力的冲击系数最大值均为0.82，大于规范[21]的推荐值0.45.

4 结 论

本文提出了一种轮胎载重车辆-大位移伸缩缝耦合系统动力学模型，并通过试验测试结果对动力学模型的有效性进行了验证，在此基础上研究了车辆对大位移伸缩缝的冲击效应，研究结果表明：

1） 车辆-大位移伸缩缝耦合系统动力学模型能有效地仿真耦合系统动态响应，仿真得到的中梁振动速度时程曲线与试验测试值趋势相同，中梁测点的振动速度最大值仿真结果与试验测试值随速度的变化趋势表现出较好的一致性，中梁测点最大下沉量与试验测试值的最大偏差小于10.0%，可满足工程精度.

2） 车辆后双轴轮胎力的冲击系数大于前轴，且车辆对大位移伸缩缝末端边梁与桥梁连接处混凝土的冲击大于对伸缩缝中梁的冲击，实际应用中应考虑对此处桥面进行加强.

3） 车辆对大位移伸缩缝中梁和伸缩缝末端桥梁的轮胎力冲击系数均随车速的增大为增大，当车速为120 km/h 时，对两者的冲击系数最大值分别为0.67 和0.82，大于我国现行规范中的局部冲击系数取0.45 的建议值. 建议在伸缩缝和桥梁端部局部结构的设计中引入车辆冲击系数时应在现有规范推荐值的基础上进行适当的放大. 同时建议进一步优化大位移伸缩缝中梁与车道线的夹角以降低车辆的冲击效应.

本文所建立的轮胎载重车辆-大位移伸缩缝耦合系统动力学模型能可靠地求解耦合系统动态响应，为大位移伸缩缝的设计和动态特性研究提供了一种计算方法，后续可以针对各参数和病害状态对大位移伸缩缝的性能影响进行进一步的研究.