基于动态罚函数的铁路车流分配与径路优化模型
薛 锋 ,刘泳博 ,户佐安 ,陈逸飞
(1. 西南交通大学交通运输与物流学院,四川 成都 611756;2. 西南交通大学唐山研究生院,河北 唐山 063000;3. 西南交通大学综合交通大数据应用技术国家工程实验室, 四川 成都 611756)
路网的车流分配及径路安排是铁路运输组织的重要内容,其优化问题主要是指在现有的路网环境、设施设备及货流条件下,合理安排车流径路,使车流在路网中的运营指标到达最优. 铁路车流分配优化能够在满足运输需求的同时,确保路网中各设施设备协调配合,合理使用车流径路,进而提高整个路网的运输效率.
目前,不少学者对铁路车流分配及径路优化问题做过研究,并取得了丰硕的成果. 纪丽君等[1-3]基于多商品流理论建立了0-1 整数规划车流分配与径路优化模型;严余松等[4]通过机会约束理论与车流量波动,构建了列车编组计划与车流径路综合优化模型;王文宪等[5]利用0-1 非线性规划模型来解决重载直达车流的分配问题;Upadhyay 等[6]基于动态规划理论优化了列车径路模型;Borndörfer 等[7]从战略层面出发,在铁路网建立了以运行时间和延误最小为目标的非线性优化模型;Yaghini 等[8]使用混合整数规划模型求解列车径路问题;Khaled 等[9]以铁路网为基础,构建了以系统总费用最小为目标函数的列车径路优化模型. 铁路车流的分配属于组合优化中的NP-hard 问题,目前的研究大多采用CPLEX、LINGO 等进行求解[10],虽有学者采用现代启发式算法,如遗传算法、模拟退火算法等,但这些算法在求解的质量和算法参数控制方面各有差异,当遇到难约束问题时,算法初始解难以产生,影响算法的求解效率. 2014 年Mirjalili 等[11]提出灰狼优化算法(grey wolf algorithm,GWO). 该算法通过模拟狼群捕食猎物过程求解优化问题,具有原理简单、可调参数少、容易实现且全局搜索能力强的优点,在函数寻优、机器学习等方面得到了有效应用[12],但目前很少有学者用该算法求解铁路车流分配及径路优化问题.
本文在文献[2]的基础上,引入虚拟弧和动态多段映射惩罚函数对模型进行改进,优化其约束条件,解决模型中的难约束问题,使模型在应对不可行流时更加灵活. 同时,运用佳点集理论对传统灰狼算法初始种群的生成进行改进,并设计收敛因子的非线性变化策略,形成一种改进的灰狼算法(improved gray wolf algorithm,IGWO),用于求解基于动态罚函数的铁路车流分配及径路优化模型.
1 铁路车流分配的基本模型
1.1 基本模型的描述
铁路车流分配问题与多商品流问题类似,即铁路的每股车流视为一种商品,那么铁路网中所有车流的分配问题可以将其视为多种商品的网络配流问题[1]. 铁路车流分配问题的本质是在满足路网约束条件的前提下,以最小的成本将车流分配到路网中. 因此,基于多商品流的铁路车流分配及径路优化基本模型通常以货物走行公里为目标函数,结合铁路路网的线路能力要求、车流不可拆散原则等构建约束条件. 图1 是由5 个车站构成的简化网络,以此为基础描述铁路车流分配及径路优化基本模型的特点. 假定技术站1 到技术站5 的车流量OD (origindestination)为8 (单位:车),各弧段参数为(B,M),B为弧段容量,M为弧段里程,车流的绕行距离不得超过最短距离的两倍.

图1 简化路网Fig. 1 Simplified railway network
如图1 所示,从技术站1 到技术站5 的路径有4 条(1→2→5,1→3→5,1→5,1→4→5),其中,路径1→5 尽管为最短路径,但不满足弧段容量的约束,路径1→2→5 满足弧段容量约束,但不满足车流的绕行距离的限制. 因此,可行路径为1→3→5,1→4→5. 考虑以货物走行公里最小为目标,最优的车流径路为1→3→5. 需要注意的是,在车流分配的过程中,必须满足同一支车流不拆散的原则.
1.2 基本模型的假设和相关参数
考虑铁路车流分配及径路优化问题的完整性和简洁性[2],基本模型包含如下假设:
1) 模型目标函数仅考虑货物在弧段中能力的约束,不考虑通过支点站的走行、改编和能力限制;
2) 每支车流在通过支点站时流量不发生变化.
铁路网简化为无向图G=(V,E) ,V为站点的集合,E为弧段的集合. 站点i,j,s,t∈V,弧段 (s,t)∈E.Ni,j为始发站i到终点站j的车流量;Bs,t为弧段(s,t)的通过能力(单位:车);M(s,t)为弧段(s,t)的里程(单位:km). 引入0-1 型决策变量yij,st表示车流Ni,j是否经过弧段(s,t),即

1.3 基本模型的构建
根据铁路车流的不可拆分原则,考虑线路能力、运输服务水平等约束,以车流的总走行里程最小为目标,基于多商品流模型构建铁路车流分配及径路优化基本模型P 如式(1) ~ (5)所示.
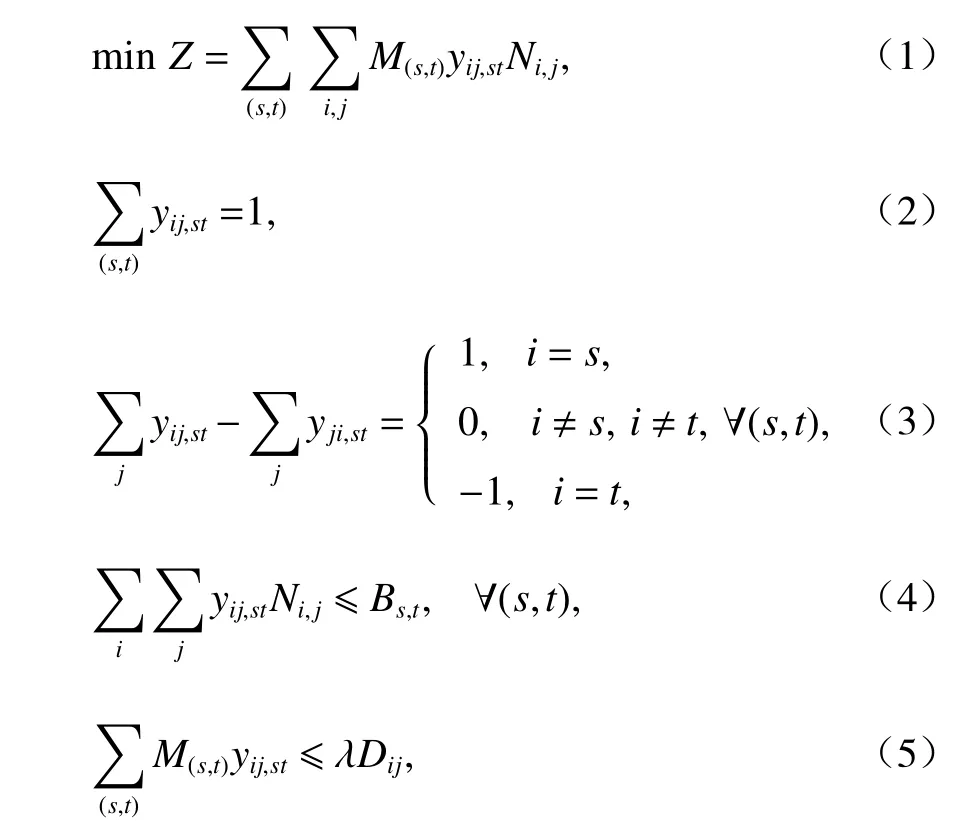
式中:Z为路网中所有车辆总的走行里程;Dij为车流Ni,j在没有能力限制下通行的最短距离;λ为最大绕行率,且 λ ≥1 .
式(1)为目标函数,表示路网中所有车辆总的走行里程最小. 式(2) ~ (5)为约束条件,式(2)体现了路网中的同一支车流不可拆分原则,式(3)为经过路网中的每个支点站的流量守恒约束,式(4)为路网中的弧段能力限制的约束,式(5)为运输服务水平约束,此处主要考虑走行距离,设置该约束可以避免少数车辆过度绕行.
2 基于动态罚函数的改进模型
铁路车流分配按照运输组织原则将多支车流分配到给定的路网中,包含具有NP-hard 特性的多商品流结构[13],属于带容量约束的径路问题(capacitated vehicle routing problem,CVRP)[14]. 为方便对CVRP 问题的求解,需要对模型进行针对性的改进,优化约束条件.
2.1 惩罚函数对模型的改进
惩罚函数具有结构简单、参数少的优点,是解决约束优化问题的一种有效方法. 借助惩罚函数可以将难约束吸收到目标函数中,便于问题求解[15]. 其惩罚策略为:对在无约束的求解过程中企图违反约束的迭代点给予很大的目标函数值,迫使无约束的迭代点向可行域靠近,或者一直保持在可行域内移动,直到收敛到原来约束最优化的极小值点.
分析模型P 可知,路网的弧段能力约束式(4)是问题的难约束,参考文献[15],并结合惩罚函数的思想,将弧段(s,t)分为真实弧和虚拟弧,并定义新的决策变量wij,st,若车流由于弧段能力限制,只能选择弧段(s,t)的虚拟弧运行,则wij,st取1,否则取0. 把新定义的变量加到目标函数中,构造增广目标函数:

式中:Z1为车流在真实弧中总的走行里程;σH(wij,st)为惩罚项,其中, σ 为惩罚力度,H(wij,st) 为惩罚因子.
当分配的车流满足弧段的容量约束时,虚拟弧上没有分配流量,H(wij,st) =0 ,目标函数不受额外惩罚;当分配的车流不满足弧段的容量约束,需要在虚拟弧上分配流量,此时H(wij,st) >0 ,目标函数受额外惩罚; σH(wij,st) 越大,惩罚越重. 要使Z极小,H(wij,st)应该充分小,当其趋近于0 时,Z的极小值逼近了Z1的极小值. 于是,有容量约束的铁路车流分配及径路优化问题即转化成了没有容量约束的优化问题. 基于惩罚函数的铁路车流分配及径路优化模型Q 如式(7)所示.
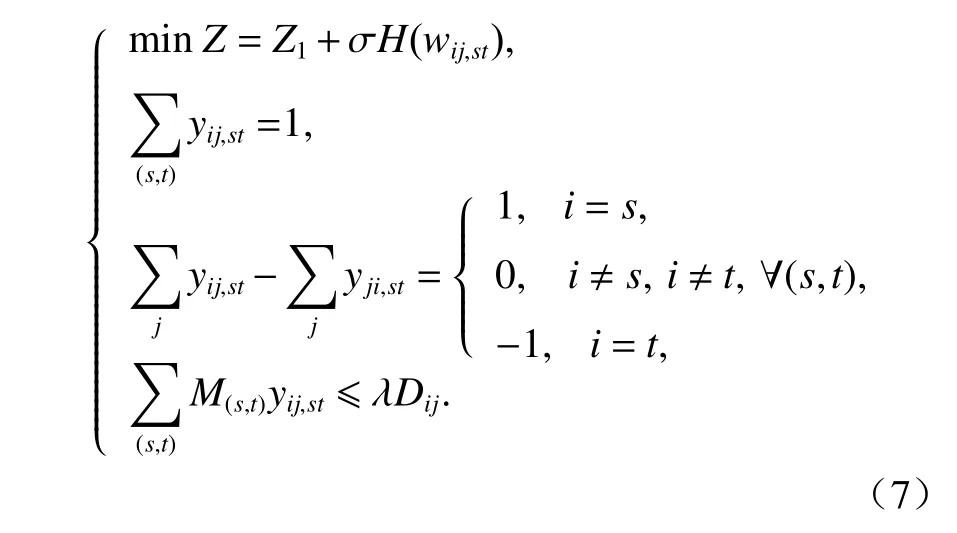
2.2 惩罚项的动态更新策略
2.2.1 惩罚力度的更新
在惩罚函数的应用过程中,需要选择合适的惩罚力度. 若惩罚力度过小,则会大大降低惩罚项对目标函数的影响,导致算法搜索时间作用于不可行域,严重影响算法求解效率;如果惩罚力度太大,则会造成增广目标函数Z过大,趋于病态,也会给模型的求解造成很大困难,甚至无法求解. 因此,选取合适惩罚力度的更新策略对算法的求解非常关键.
惩罚力度在优化过程中的变化依赖于当前群体中可行解所占的比例[16],本文在文献[16]基础上提出一种动态调整惩罚因子的策略. 第k次迭代过程中,惩罚力度的更新规则为

式中: ρk为在第k次迭代过程中,满足弧段容量约束的个体所占种群数量的比值.
惩罚力度的更新规则具有以下性质:
1) 函数结构简单,其参数不需要人为调整.
2) σk随着种群中可行解的比例而变化,种群中的可行解比例高,则 σk较小;反之,种群中的可行解比例低,则 σk较大. 该函数的初值并不是人为给出,是由当前种群的状态决定.
3) 在算法优化的过程中,如果 σk较大,则会有更多的可行解进入种群,此时的 σk将会随之减小;反之,如果 σk较小,则会有更多的不可行解进入种群, σk也将会随之增大. 由此可以看出,本文设计σk的更新函数是动态的,自适应的.
4) 在可行解的比值 ρk从0 变化到1 的过程中,前期 σk急剧减小,后期 σk减小缓慢,如此可以使算法从搜索可行解的过程中快速转移到最优目标函数的搜索.
5) 式(8)中的 ( 2k-1)/k是值域为[1, 2)的增函数,这样设计可以在算法迭代的初期降低惩罚函数的影响,从而保留较多的不可行解来增加种群的多样性,在后期增加惩罚函数的影响,从而保留较多的可行解来确保目标函数的寻优.
2.2.2 惩罚因子的更新
通过非固定阶段映射惩罚力度的方法可以解决约束优化问题,避免固定罚函数中惩罚因子难以确定的缺陷[17]. 基于该思路,结合文献[17]的多阶段映射罚函数的表达式,对优化模型Q 中的惩罚因子修正为
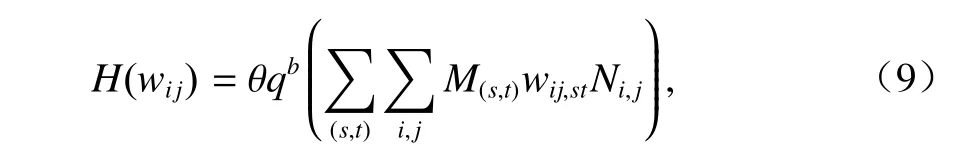
式中:q为对容量约束的违背程度,其值等于虚拟弧中总车流量与真实弧中总车流量的比值,如式(10)所示;b为惩罚函数的强度大小,如式(11)所示;θ为分段映射函数,通过和真实弧的流量对比确定多阶段映射罚函数各个区间的函数值,如式(12)所示.
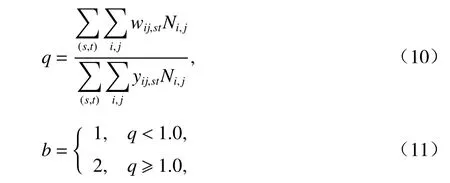

3 灰狼算法的改进
3.1 GWO
3.1.1 狼群的社会等级
灰狼算法在迭代过程中,根据适应度值的大小,将狼群划分 α 、 β 、 δ 、ω4 个等级,其中, α 、 β 、 δ 为适应度值排名前3 的头狼,剩余的狼群为ω. 计算过程中,狼群ω实现整个算法的寻优过程,3 只高等级的狼 α 、 β 、 δ 被假设拥有获取猎物位置的潜在能力,共同指挥狼群ω的移动,然后狼群ω将信息反馈给上层的3 只狼,由他们决定是否需要更新信息. 当达到算法的迭代次数时, α 、 β 、 δ 分别对应所求解问题的最优解、次优解、次次优解.
3.1.2 狼群的捕食过程
狼群捕食过程分为包围猎物和攻击猎物,狼群先通过包围猎物寻找到进行狩猎的最佳路线,然后对猎物进行攻击,最后达到捕食猎物的目的. 狼群的捕食过程用式(13) ~ (15)进行描述.
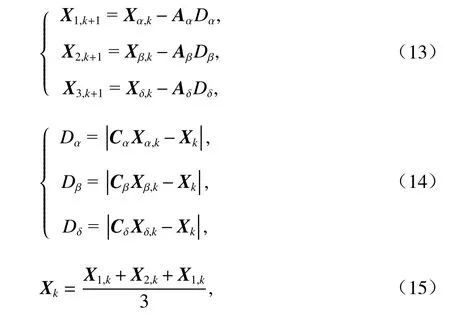
式中:X1,k、X2,k、X3,k分别为狼群ω相对3 只头狼 α 、 β 、δ在第k次迭代时的位置向量;Xm,k为头狼m在第k次迭代时的位置向量,m∈{α,β,δ};Dm为头狼m到狼群ω间的距离;Xk为第k次迭代时狼群ω的位置向量;Am、Cm为系数向量,分别为

其中:r1、r2为随机向量,且0≤ |r1| ≤1,0≤ |r2| ≤1;ak= 2(1-k/K),为收敛因子,K为最大迭代次数.
3.2 IGWO
3.2.1 初始种群的优化
对群智能算法而言,初始种群的好坏影响算法的求解效率和性能,多样性较好的初始种群有助于提高群智能算法的寻优能力. 根据文献[18]可知:均匀取点能够较好地保证初始种群的多样性,并且佳点集序列的取点方式比其他方式的取点更为均匀. 但是,GWO 在形成初始种群的过程中是通过随机数产生,无法保证初始种群的个体在搜索空间中均匀分布. 因此,为克服这一不足,本文采取佳点集序列的方式对GWO 初始种群的形成进行优化. 图2 给出了随机序列和佳点集序列在二维搜索空间(x,y) ( 1 00×100 )中生成的100 个个体的初始种群分布. 从图2 可以看出:佳点集方式形成的初始种群个体分布更加均匀,并且具有较好的多样性.
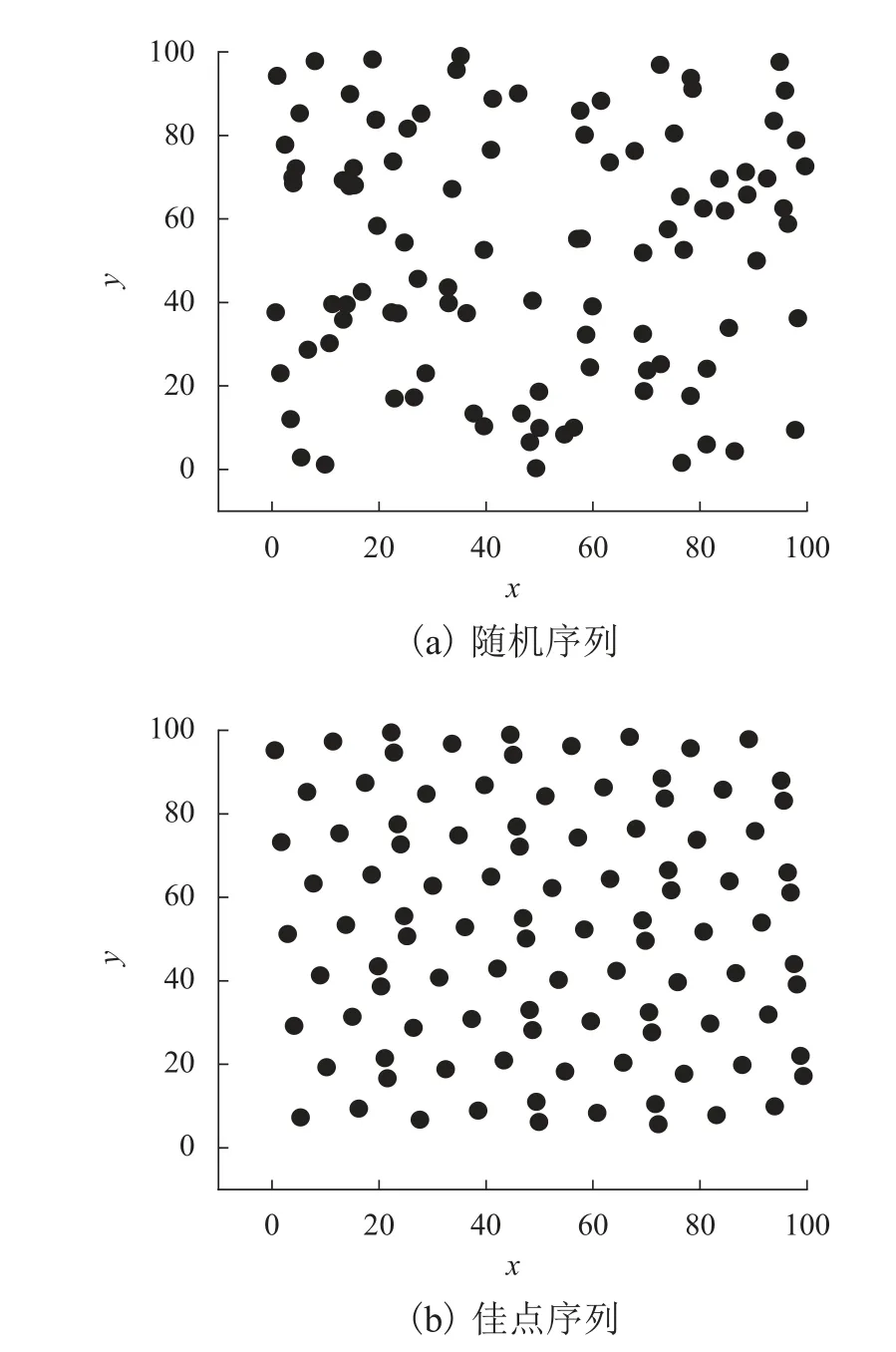
图2 两种方式下初始种群的分布Fig. 2 Distribution of initial population in two modes
3.2.2 收敛因子的改进策略
在GWO 算法中,随着算法的不断迭代,收敛因子ak从2 线性递减至0. 但是,线性变化的收敛因子不能很好地平衡算法的全局搜索能力和局部搜索能力[19]. 对此,本文根据余弦函数前期下降慢后期下降快的特点,设计一种基于余弦函数的收敛因子,如式(18)所示.

ak随着迭代次数呈非线性递减. 在迭代初期,ak下降较慢,算法保持较大的搜索步长,可以更好地寻找全局最优解;而到了后期,ak下降较快,搜索步长快速减小,从而使狼群更加集中,能够更加精确地寻找到局部最优解.
4 求解改进模型的IGWO 算法设计
4.1 编码策略
本文提出的IGWO 采用先路由后分组的策略生成多支车流的可行路径集,为了满足式(2)、(3),采用整数编码,编码规则为:将狼群中的第e个灰狼个体的位置向量Xe与各支车流序号形成映射关系,Xe= (xe,1,xe,2,···,xe,p,···,x1,n),xe,p为第e个灰狼个体第p个OD 车流在其所在的可行路径集中选择的径路编号,p= 1,2, · ··,n,n为OD 车流个数,然后按照车流的顺序依次访问所对应的可行路径集,可行路径集的大小由式(5)决定,每支车流在其所在的路径集中有且只能选择一条径路. 具体的编码操作如图3 所示,图中:mp为第p个OD 车流的可行路径集中的径路个数;x1,x2,···,xn为灰狼位置分量.
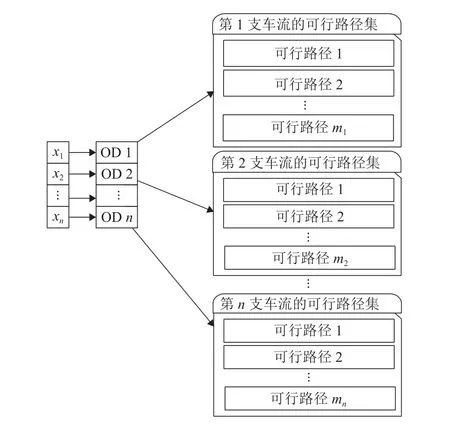
图3 编码操作Fig. 3 Encoding operation
4.2 求解步骤
IGWO 在求解模型Q 的步骤如图4 所示.
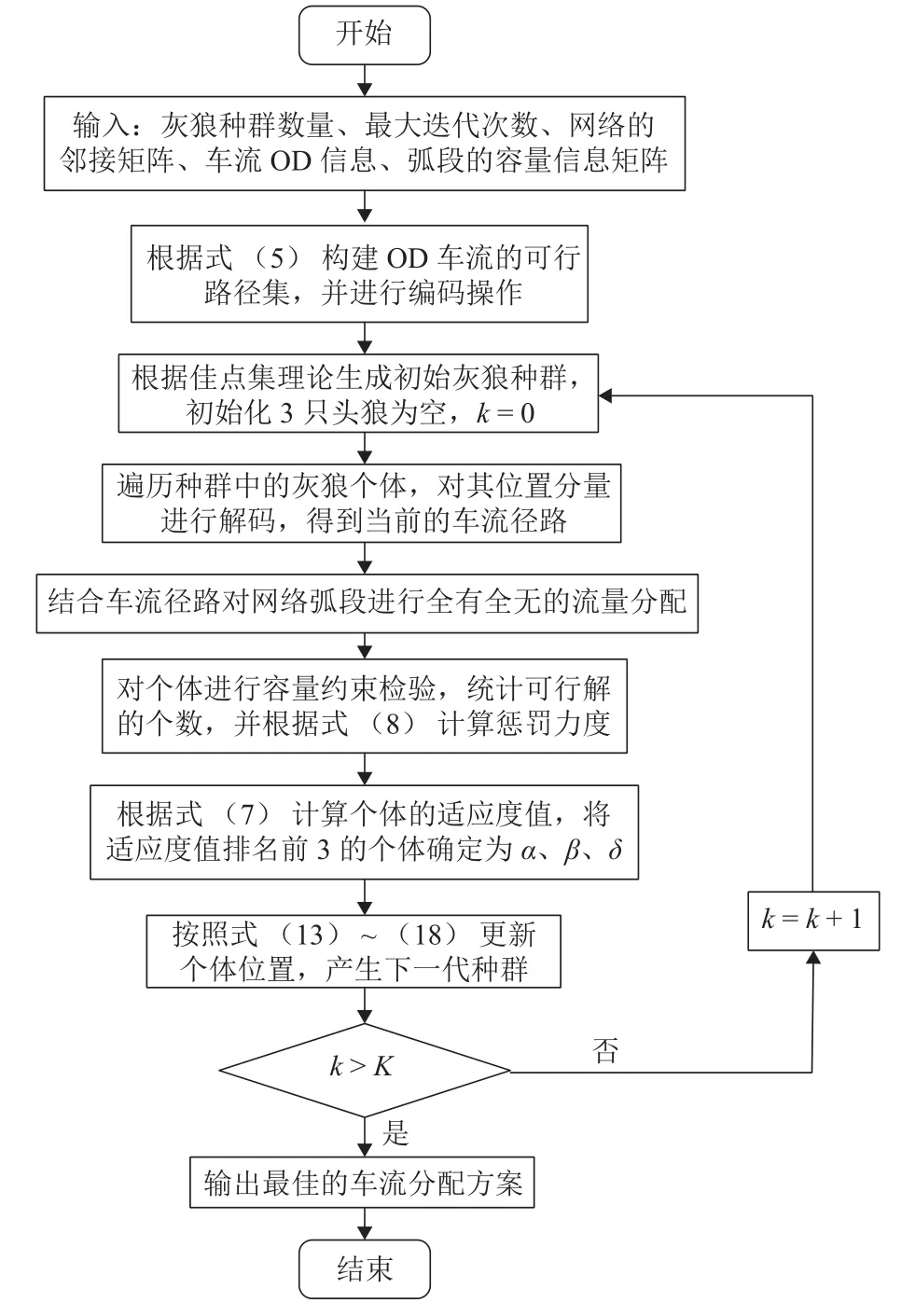
图4 IGWO 在求解模型Q 的流程Fig. 4 Flowchart of IGWO solving model Q
5 算例分析
5.1 基础数据
本文采用模拟的车流OD 数据,在区域铁路网[2]上对模型和算法进行验证. 模型涉及的站点和弧段的邻接关系如图5 所示,该路网由14 个支点站和20 条弧组成.
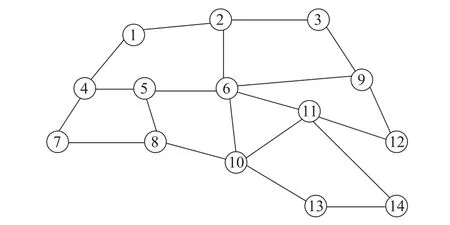
图5 某区域简化路网Fig. 5 Simplified railway network of a certain area
路网其他属性参数、各区段之间的里程以及线路的容量见表1. 线路的容量为该弧段上、下行车流年通过能力的总和,20 支模拟车流OD 量及发到站见表2.
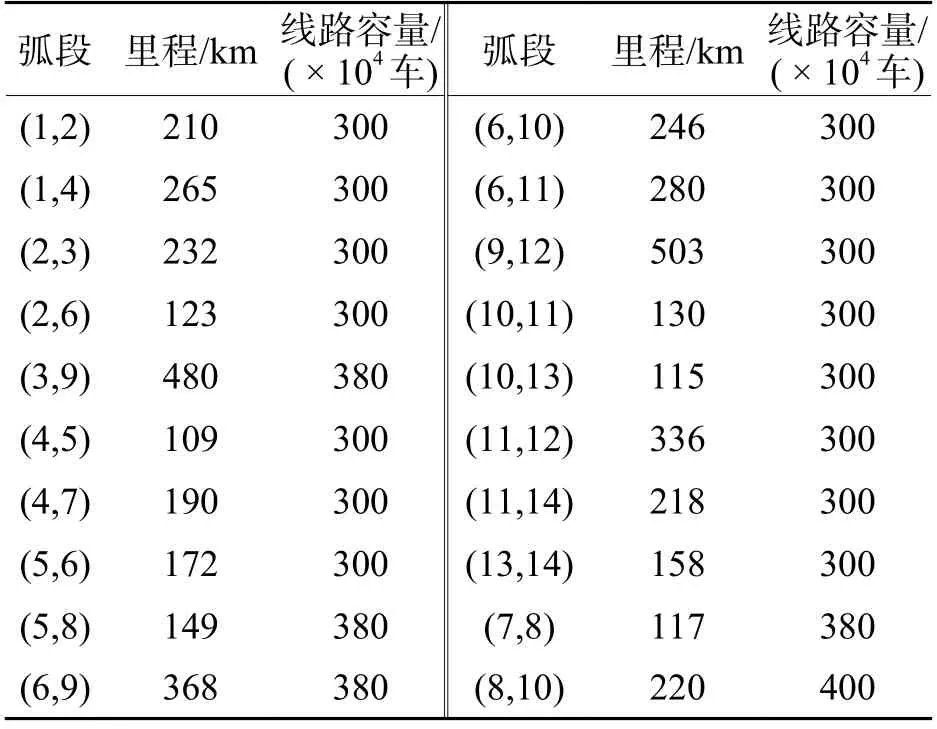
表1 路网相关参数Tab. 1 Railway network parameters
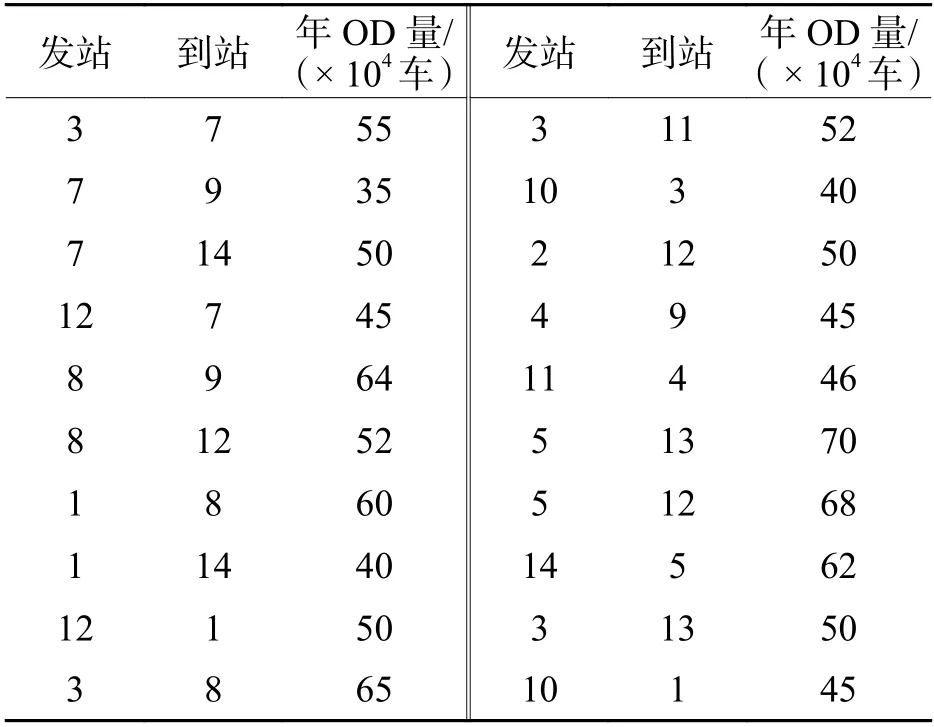
表2 年车流OD 量Tab. 2 Annual OD volume of cargo flow
5.2 模型求解
基于上述路网结构和参数,在处理器为i7-7 700 HQ 四核2.8 GHz 的个人计算机上,使用MATLAB 2018 进行编程求解. 算法的参数设置如下:种群规模为80,最大迭代次数为100 次,最大绕行率为2.经过37 s 的计算,各支车流优化后的走行径路如表3所示. 在20 支OD 车流中,按最短径路运输的有6 支车流,分别为N7,14、N10,3、N2,12、N14,5、N10,1、N14,5,其余车流因为线路容量的限制均发生了不同程度的绕行.
5.3 结果分析
5.3.1 弧段容量限制检验
为验证表3 中的最佳配流方案是否满足容量的约束,需要对各个弧段的流量进行统计. 经计算,各弧段的通过车流量及其通过能力占用情况如表4 所示. 在表4 中,部分弧段的能力利用率高达90%以上,如弧段(2,6)、(5,8)、(13,14)、(8,10),而弧段(4,5)、(5,6)、(9,12)的能力利用率低于50%,并且所有弧段车流的通过量均小于弧段能力的上限,满足模型中弧段容量限制约束.

表3 车流径路的优化方案Tab. 3 Optimization scheme of cargo flow route

表4 区间通过流量统计Tab. 4 Interval traffic statistics
5.3.2 改进前后模型的结果对比分析
为验证动态惩罚函数对模型求解的影响,应用GWO 和IGWO 分别对改进前、后的模型进行求解,对其求解10 次,并取车流总走行公里的均值,结果如表5 所示.
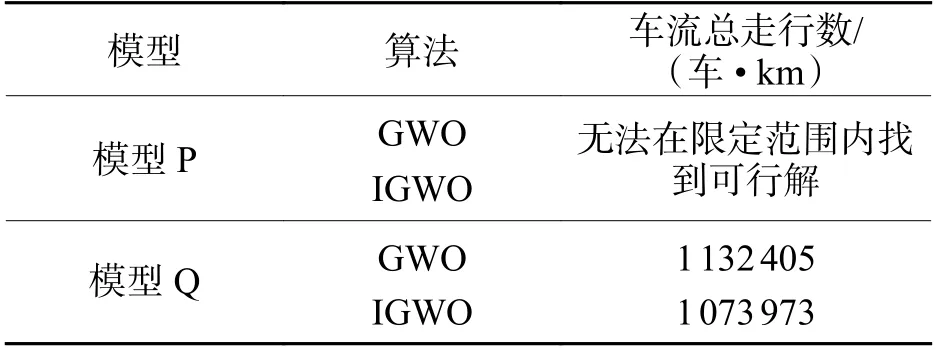
表5 改进前后模型的车流总走行公里Tab. 5 Cargo flow kilometers before and after improving model
从表5 可以看出:由于模型P中包含的弧段容量约束的限制,直接用GWO 和IGWO 难以在限定范围内找到可行解,这说明,群智能算法在直接求解难约束问题时有着自身的局限性.
对模型进行约束优化后,通过GWO 和IGWO可以求得满足约束条件的可行解,这说明本文基于惩罚函数提出的约束优化策略,克服了群智能算法在求解难约束问题时的局限性,并且可以应用于CVRP 问题的求解.
5.3.3 算法的性能分析
1) 解的质量
本文选取20 个OD 车流径路的平均绕行率、选择最短路径的OD 个数以及目标函数作为衡量两种算法解的质量指标,结果如表6 所示.

表6 两种算法的质量指标Tab. 6 Quality metrics for two algorithms
从表6 可以看出:相比于GWO,IGWO 路径平均绕行率下降了2.6%,车流总走行公里下降了5.2%,且IGWO 选择最短路径的OD 数也多于GWO.
2) 收敛性能
如图6 所示,IGWO 在算法迭代的初期就开始收敛,在第13 代的时候达到最优,其收敛速度与求解的结果均优于GWO.

图6 GWO 和IGWO 的求解示意Fig. 6 Solution illustration of GWO and IGWO
综上,本文提出的初始种群和收敛因子的改进策略在一定程度上避免了GWO 容易陷入局部最优的不足,使其在解空间的搜索能力上有了较大提高.
6 结 论
本文引入动态更新的惩罚函数对铁路车流分配及径路优化模型中的弧段容量约束进行优化,并设计改进灰狼算法对其进行求解,通过算例验证,得到以下结论:
1) 通过弧段容量限制的检验分析发现,本文基于惩罚函数提出的改进模型求得的配流方案满足弧段容量约束.
2) 通过对改进前后模型的结果分析发现,本文提出的对容量约束进行优化的策略可以有效解决GWO 无法处理难约束问题的不足,使其可以在限定的条件下找到满足约束条件的可行解.
3) 通过GWO 和IGWO 分别对改进后的模型进行求解可知,与GWO 的求解结果相比,IGWO 求得的配流方案使OD 车流的平均绕行率下降了2.6%,货物走行公里数下降了5.2%,并且收敛速度也优于GWO,从而体现了本文所提出的对GWO 改进策略的有效性.

