利用函数的性质求参数的取值范围
田素伟
(上海市泥城中学 201306)
函数和不等式是历年高考的重点和难点,近年来,数学高考中出现了一些重视基础、考查能力的新型试题,特别是在不等式恒成立或方程的问题中含参数的问题更是精彩纷呈,如何求这类问题中参数的取值范围?下面就常见的几种题型分别举例说明.
1 构造函数求参数的取值范围
例1 如果x∈[2,3]时,不等式2021x+a-2021ax2+1≥2022-x-a-2022-ax2-1恒成立,求实数a的取值范围.
解析由2021x+a-2021ax2+1≥2022-x-a-2022-ax2-1,可得
2021x+a-2022-x-a≥2021ax2+1-2022-ax2-1.
构造函数f(x)=2021x-2022-x,
由此可知f(x)=2021x-2022-x在(-∞,+∞)是增函数.
所以f(x+a)=2021x+a-2022-x-a,
f(ax2+1)=2021ax2+1-2022-ax2-1.
由2021x+a-2022-x-a≥2021ax2+1-2022-ax2-1可得f(x+a)≥f(ax2+1).
所以x+a≥ax2+1.
所以原题可化为:当x∈[2,3]时,不等式x+a≥ax2+1恒成立,求实数a的取值范围.
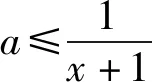
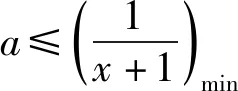
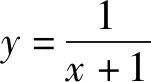
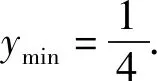
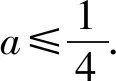
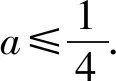
2 双变量问题先确定主变量求参数的取值范围
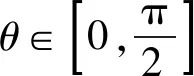
分析本题中有两个变量m和θ,题目中含有符号f,如何去掉f,利用函数的单调性即可.
解析由f(x)=x2021+x,显然f(x)为奇函数,且单调递增.
因为f(msinθ)+f(1-m)>0恒成立,
所以f(msinθ)>f(m-1)恒成立.
所以msinθ>m-1恒成立.
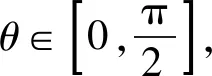
这里有两个变量m和t,因为t的取值范围已经确定,所以确定以t为主变量,把不等式转化为关于t的函数,设f(t)=mt-m+1,
(1)当m=0时,此时f(t)=1>0符合题意;
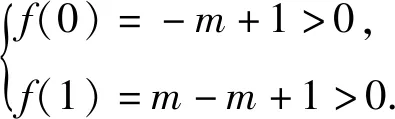
解得m<1且m≠0.
在进行完现场勘察后,根据所获得的实际情况以及相关资料,特别是安全要求和技术要求,来进行运维现场的危险源辨识、危险点预测等。所谓危险源辨识指的是系统分析作业现场的实际情况,对有危险隐患存在的位置、方式以及可能发生事故的规律和途径来进行分析和辨识。在实际的辨识危险源过程中,要进行责任制,安排专门的负责人和工作人员来细分责任。全面排查现场的各方面隐患,由负责人实施落实。
由(1)(2)可知:实数m的取值范围是(-∞,1).
评析本题利用函数的性质转化为关于两个变量m和t的不等式,因为t的取值范围已经确定,所以确定以t为主变量,把不等式转化为关于t的函数,一般情况下含两个变量m和t的不等式,如果其中一个变量的取值范围能确定,那么就以这个变量为主变量,另外一个变量作为参数.
3 在任意和存在性问题中求参数的取值范围
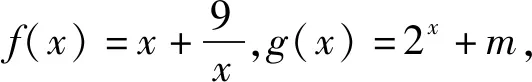
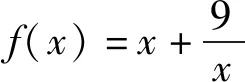
所以函数f(x)max=f(1)=10.
因为g(x)=2x+m在区间[2,3]上单调递增,
所以g(x)max=23+m=8+m.
所以10≤8+m.
所以m≥2.
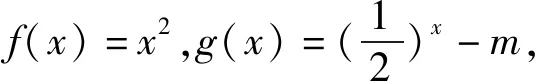
解析因为对∀x1∈[-1,3],∃x2∈[0,2],f(x1)≥g(x2),所以只需f(x)min≥g(x)min即可.
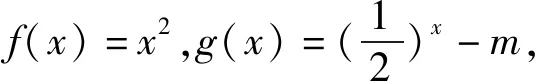
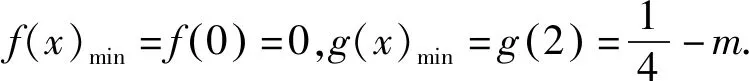
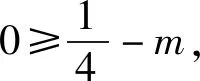
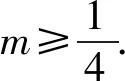
4 利用数形结合求参数的取值范围

分析首先通过函数图象变换作出f(x)的图象(如图1),因为关于f(x)的一元二次方程[f(x)]2+bf(x)+c=0最多只能解出2个f(x),若方程要恰有七个不相同的实数解,设[f(x)]2+bf(x)+c=0的两个根分别是f1(x),f2(x),所以两个函数值f1(x),f2(x)共对应7个不同的x,假设函数值f1(x)对应3个不同的x,f2(x)函数值共对应4个不同的x,设t=f(x),所以函数y=t与y=f1(x)图象的交点是3个,函数y=t和y=f2(x)的图象的交点是4个,由图象可知t=1或t=0时,即f1(x)=1,函数y=t与y=f1(x)图象的交点是3个,由图象可知0 解析首先通过函数图象变换作出f(x)的图象(如图1). 图1 因为关于f(x)的方程[f(x)]2+bf(x)+c=0最多只能解出2个f(x),若方程要恰有七个不相同的实数解,设[f(x)]2+bf(x)+c=0的两个根分别是f1(x),f2(x), (1)设当f1(x)=1,0 方程的两个根分别是t1,t2, 所以t1=1,t2∈(0,1). 所以由根与系数的关系可得t1+t2=-b. 所以t2=-t1-b,即t2=-1-b∈(0,1). 所以0<-1-b<1. 所以-2 (2)设当f1(x)=0,0 因为[f(x)]2+bf(x)+c=0,所以t2+bt+c=0. 方程的两个根分别是t1,t2,所以t1=0,t2∈(0,1). 所以由根与系数的关系可得t1+t2=-b. 所以t2=-b. 所以0<-b<1,即-1 所以实数b的取值范围是-2 分析根据条件先分析f(x)+f(-x)的结果,由此确定出g(x)=f(x)+1的奇偶性和单调性,再将问题转化为“已知g(2a-1)≤g(2-a2),求解a的取值范围”,根据单调性列出关于a的不等式并求解出结果. 解析由题可知x∈R且 所以f(x)+1=-[f(-x)+1]. 设g(x)=f(x)+1,所以g(-x)=f(-x)+1. 即g(-x)=-g(x). 又函数g(x)的定义域为R关于原点对称, 所以g(x)是奇函数. 由函数的性质可知: 所以f(x)在(0,+∞)上单调递增. 即g(x)在(0,+∞)上也单调递增且g(0)=0. 又因为g(x)为奇函数, 所以g(x)在R上单调递增. 不等式f(2a-1)+f(a2-2)≤-2 ⟺f(2a-1)+1≤-[f(a2-2)+1], 所以g(2a-1)≤-g(a2-2)=g(2-a2). 所以2a-1≤2-a2. 解得-3≤a≤1.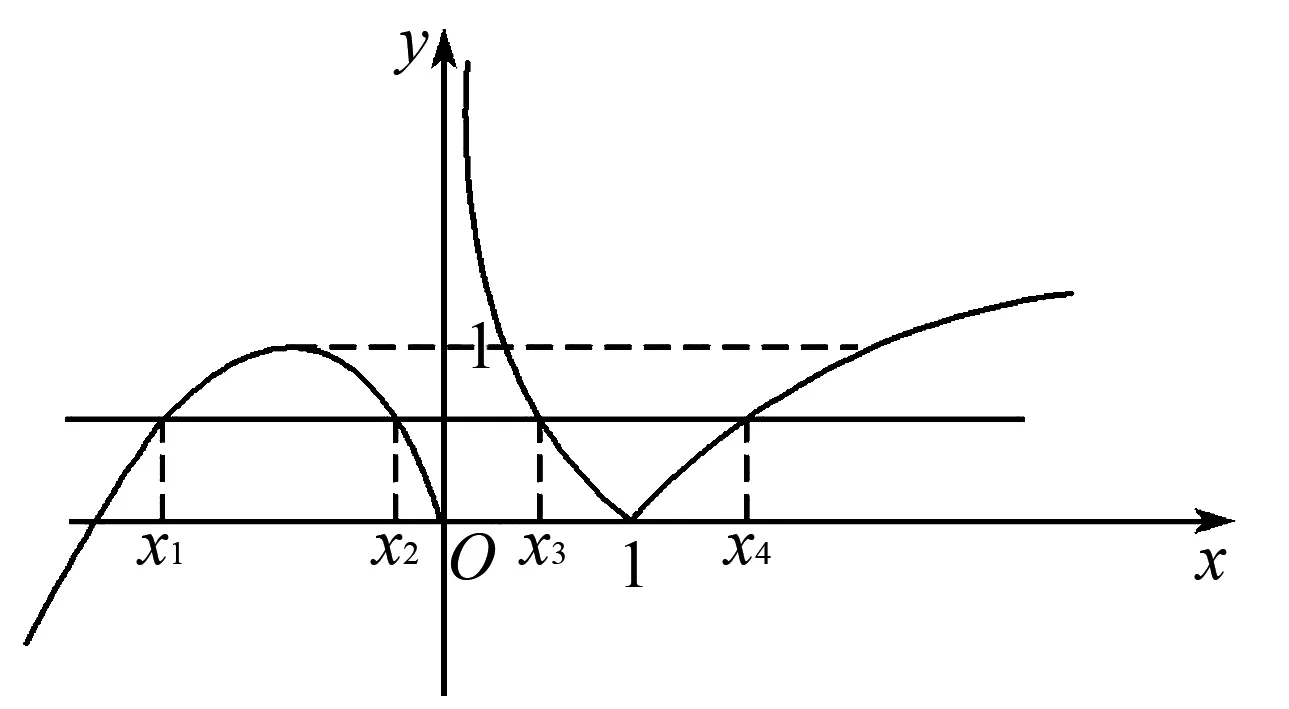
5 利用函数的奇偶性求参数的取值范围