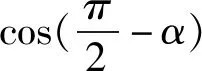从关联速度入手 让思维进阶发生
史剑辉
(安徽省灵璧中学 234200)
1 问题提出
如何对关联速度进行有效地复习教学,让深度学习真正发生在学生身上,使学生的思维能力在课堂上进阶呢?本文将从三个阶段,针对学生学习的实际情况,通过改变物理题设条件,实现思维的三层递进,达到培养学生物理核心素养、具备解决实际问题的能力.第一层次是几乎所有学生都知道的将合速度分解为沿绳(杆)方向的分速度和垂直于绳(杆)方向的分速度,两物体沿绳(或杆)方向分速度大小相等;第二层次是接触处两物体沿弹力方向的分速度相等;第三层次由能量守恒定律列方程求解.
2 思维进阶
2.1 绳物连接
例1(多选)如图1所示,做匀速直线运动的小车A通过一根绕过定滑轮的长绳吊起一重物B,设重物和小车速度的大小分别为vB、vA,则( ).
A.vA>vB
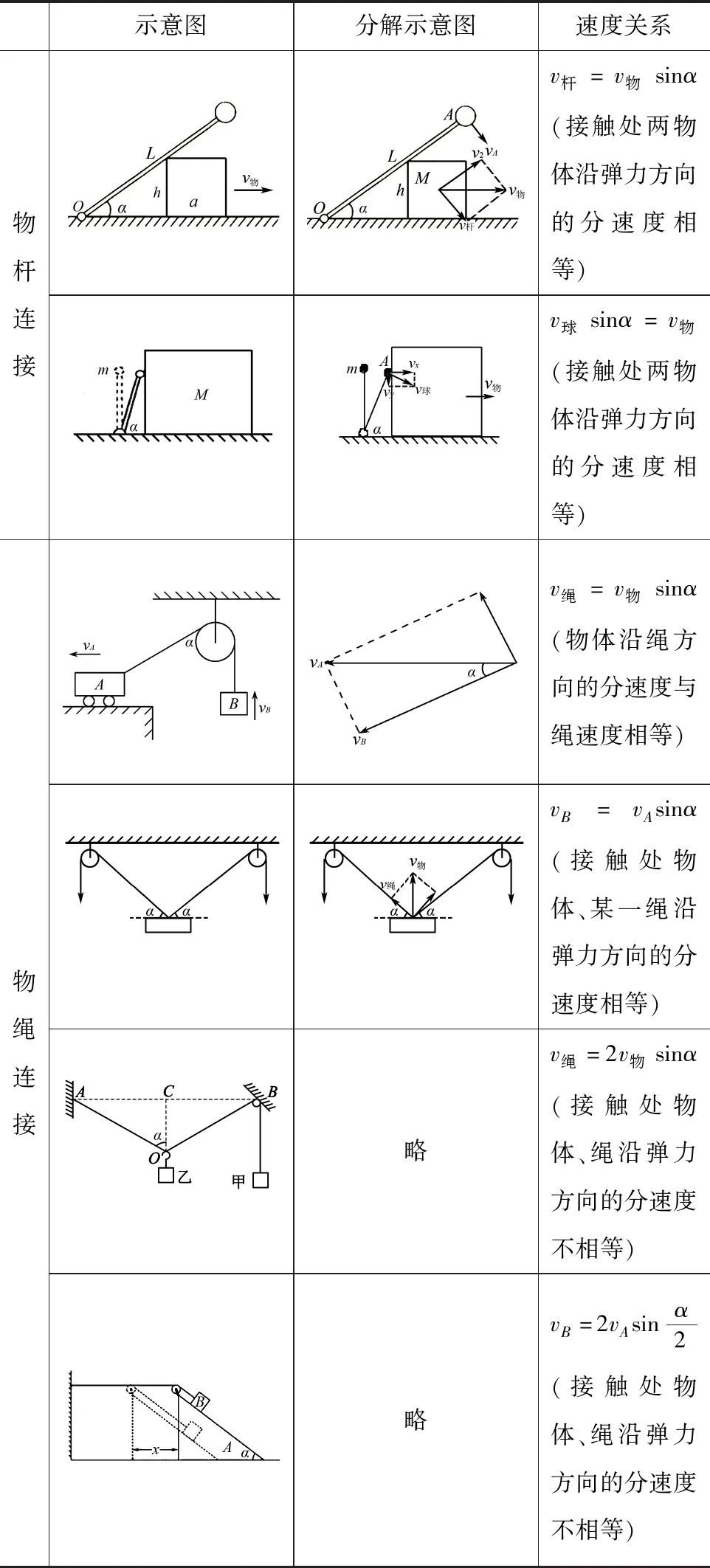
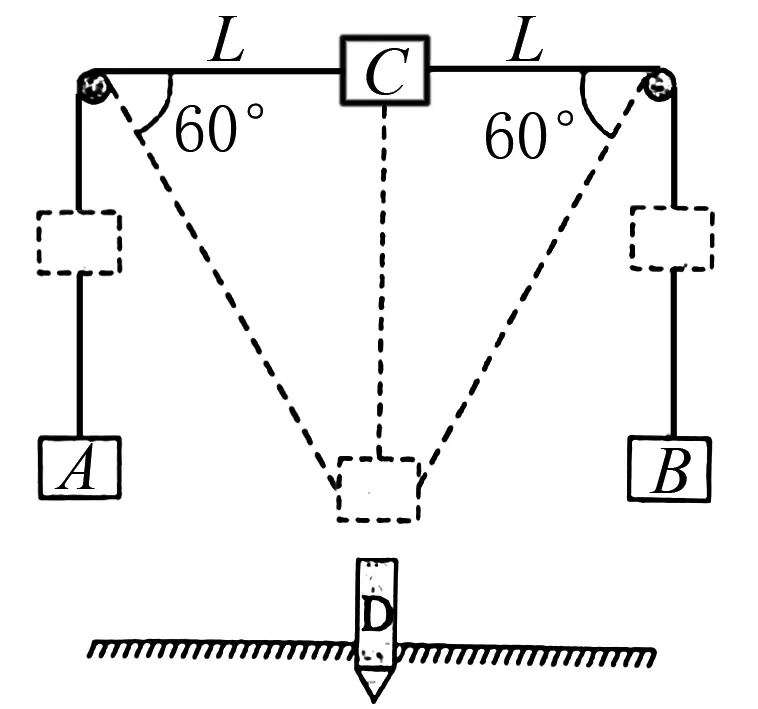
B.vA C.绳的拉力等于B的重力 D.绳的拉力大于B的重力 图1 图2 解析小车A向左运动的过程中,小车的速度是合速度,可分解为沿绳方向的分速度与垂直于绳方向的分速度,如图2所示,由图可知vB=vAcosθ,则vA>vB,小车向左运动的过程中θ角减小,vB增大,B向上做加速运动,故绳的拉力大于B的重力.选项A、D正确. 点评本题考查关联速度问题,旨在引出关联速度的概念和基本解题方法,引导学生绳(或杆)与物体接触时,若绳(或杆)与物体的运动方向不共线时二者的速度关系.学生们都会按套路“将合速度沿绳(或杆)方向和垂直绳(或杆)方向进行分解,两物体沿绳(或杆)方向分速度大小相等”求解.这是思维的第一阶段,用此方法也能完成好些试题,但这个结论具有广泛性吗? 例2 如图3所示,长为L的轻杆一端用铰链固定于O点处,另一端固定小球A,杆靠在质量为M、高为h的物块上.若物块以速度v向右运动且杆与物块始终保持接触,则当杆与水平方向的夹角为θ时,小球A的速率为( ). 图3 图4 (1)求C的质量; (2)若D在运动过程中受到的阻力F可视为恒力,求F的大小; (3)撤掉桩D,将C再次拉到图中实线位置,然后由静止释放,求A、B、C的总动能最大时C的动能. 图5 示意图分解示意图速度关系物杆连接v杆=v物sinα(接触处两物体沿弹力方向的分速度相等)v球sinα=v物(接触处两物体沿弹力方向的分速度相等)物绳连接v绳=v物sinα(物体沿绳方向的分速度与绳速度相等)vB=vAsinα(接触处物体、某一绳沿弹力方向的分速度相等)略v绳=2v物sinα(接触处物体、绳沿弹力方向的分速度不相等)略vB=2vAsinα2(接触处物体、绳沿弹力方向的分速度不相等) 归纳总结:关联速度问题本质上是能量守恒定律在运动的合成与分解中的具体应用,只有回归到能量守恒定律,问题才能迎刃而解了,背一些碎片化的结论,那都是不全面的. 将部分关联速度结论汇总如表1所示. 关联速度是运动板块中一类重要的物理问题,是运动合成与分解的典型代表,也是学生学习的重点、难点、甚至是痛点.本文针对学生学习的实际情况,通过改变物理题设条件,实现思维的三层递进,让学生在课堂上学习深度,实现思维进阶,如果学有余力的学生,教师还可设计不同类型的关连新情景,如:两线交点关连,照射关联等,还可用其他的方法拓展学生的视野,如:位移分解法(微元法)、导数法、等量分解法、相对运动法、转换参考系法、功能关系法等求解,在课余进一步提升自己的素养,提高物理解题能力.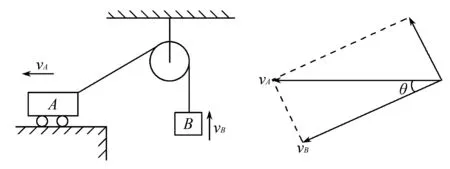
2.2 杆物连接

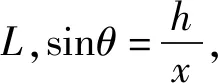
2.3 多绳物连接
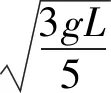
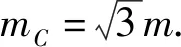
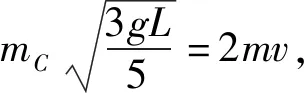
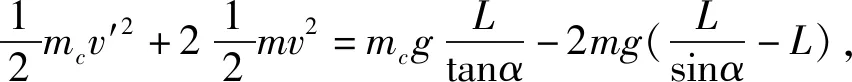
2.4 总结提升