数列求和之裂项相消法
2022-11-03 04:13李发明
数理化解题研究 2022年28期
李发明
(山东省泰安第一中学 271000)
数列问题在高考中常常是以求通项公式、求前n项和的考查形式出现.在数列求和问题中,裂项相消法占有举足轻重的地位.本文对裂项相消法的多种类型进行梳理和归纳.







所以an=n.

推广类似地,我们还可以求出通项公式为



或en=n·n!=(n+1)!-n!的数列的前n项和.
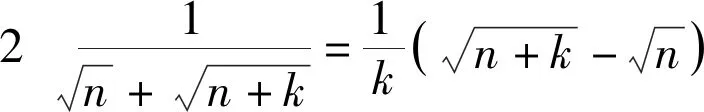







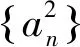





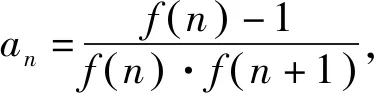


所以f(x)=2x+1.




(1)求数列{an}的通项公式;
解析(1)an=3n-1(过程略).
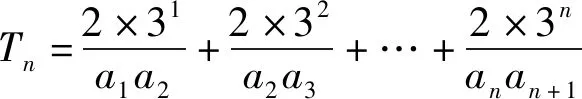

例4(2014年山东)已知等差数列{an}的公差为2,前n项和为Sn,且S1,S2,S4成等比数列.
(1)求数列{an}的通项公式;
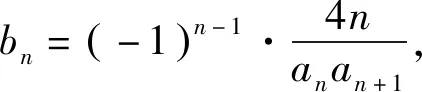
解析(1)因为{an}的公差为2,
所以Sn=a1n+n(n-1).
所以(2a1+2)2=a1(4a1+12).
解得a1=1.
所以an=2n-1.

当n为奇数时,
当n为偶数时,

练习4在公差不为零的等差数列{an}中,a1=2,且a1,a2,a4成等比数列.
(1)求数列{an}的通项公式;

解析(1)an=2n(过程略).

当n为奇数时,
当n为偶数时,

猜你喜欢
汽车实用技术(2022年7期)2022-04-20
客联(2021年4期)2021-09-10
福建中学数学(2021年8期)2021-03-01
中学生数理化(高中版.高考数学)(2019年10期)2019-11-08
中学生数理化·高三版(2017年1期)2017-04-20
教学月刊·中学版(教学参考)(2016年8期)2016-07-27
数学教学通讯·高中版(2016年4期)2016-05-27
消费电子(2014年3期)2014-03-22
中学生数理化·高一版(2008年1期)2008-11-15
中学数学杂志(高中版)(2008年2期)2008-07-31

