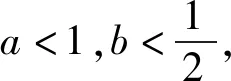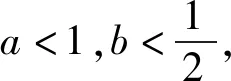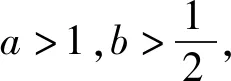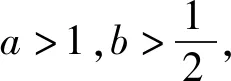利用函数思想比较大小
李文东
(广东省中山市中山纪念中学 528454)
函数思想是用运动和变化的观点,分析和研究数学中的数量关系,建立函数关系或构造函数,运用函数的图象和性质去分析问题、转化问题,从而使问题获得解决.利用函数思想解题指的是一种意识,一种解题时的思维习惯,具体说就是用变量和函数的观点来思考问题.对于比较大小问题,我们利用函数思想去思考,往往可以起到简化的作用.
1 把字母看作变量或把代数式看作函数
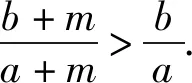
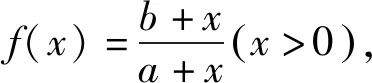
由于a>b>0,故b-a<0.
因此函数f(x)在(0,+∞)上单调递增.
故f(x)>f(0).
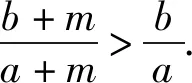
例2 设实数a,b,c满足a>b>1,c>1,则下列不等式不成立的是( ).

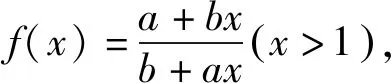
由a>b>1知,函数f(x)在(1,+∞)上单调递减.
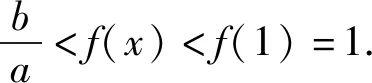
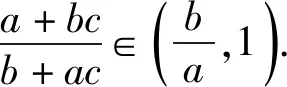
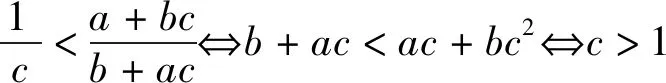
本题答案为D.
点评例1虽然用不等式的性质也很容易证明,但是利用函数的思想求解则是从另外一个角度看问题,这在例2中其优点就很明显,例2若是用不等式的知识求解就比较困难.
2 利用函数的性质比较大小
例3设a,b,c>0,且a2+b2=c2,n∈N*,且n≥3,试判断an+bn与cn的大小.

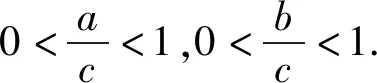

从而f(n) 即an+bn 例4(多选题) 若a>b>0,则下列不等式中一定成立的有 ( ). 故f(a)>f(b). 本题答案为AC. 点评本题构造函数的方法称为同构法,同构法是目前高考比较热门的比较大小的方法.数学中的同构式是指除了变量不同,而结构相同的两个表达式.许多比较大小的问题,通过等价变形,可以转化为同构式,然后构造函数,利用函数的单调性求解. 例5(多选题)下列不等关系正确的有( ). 故本题答案为ACD. A.c C.a 解析令x=0.01,则x∈(0,1). <0. 故f(x)在(0,1)上单调递减. 于是f(x) >0. 故g(x)在(0,1)上单调递增. 于是g(x)>g(0)=0.即a>c. 综上,b 点评本题中a,b,c非常接近,又涉及到对数和根式的运算,直接很难比较,三个数中的1.01,1.02,1.04非常接近,因此引入x=0.01构造函数来比较大小,比较巧妙! 例7(多选题)已知a>b>0,下列选项中正确的为( ). B.若a2-b2=1,则a-b<1 C.若2a-2b=1,则a-b<1 D.若log2a-log2b=1,则a-b<1 解法1 (特值法)取a=4,b=1可知A错误;取a=4,b=2可知D错误,故本题选BC. 对于C选项,由2a-2b=1⟹2a-b=1+2-b<2,得a-b<1,故C正确; 或设2a=x,2b=y,则 a=log2x,b=log2y,且x-y=1, 对于D选项,由log2a-log2b=1可知a=2b,故a-b=b不一定小于1,故D错误;故本题选BC. 令f(x)=x2,则f(a)-f(b)=1,注意到f(1)-f(0)=1,而f′(x)=2x,f″(x)=2>0,可见f(x)的增长速度越来越快,故a-b<1; 令f(x)=2x,则f(a)-f(b)=1,注意到f(1)-f(0)=1,而f′(x)=2xln2,f″(x)=2xln22>0,可见f(x)的增长速度越来越快,故a-b<1; 图1 图2 图3 图4 由图象易知本题选BC. 点评本题四种解法,解法1仅仅是作为选择题的解题策略,其对于BC的正确性并没有真正证明;解法2的解法极大地依赖代数变形,不同的选项其变形方式不一样;解法3和解法4则是从函数这个统一的角度去思考问题,解法3借助函数增长速度(二阶导函数的符号),解法4从数形结合的角度思考. 例8 已知实数a,b满足关系式a2=b2-b+1,则下列结论正确的是( ). 点评本题实数a,b满足关系式a2=b2-b+1虽然不是函数关系式,但是借助函数的思想(变化的观点)利用数形结合就很容易得到答案D,若是用不等式的知识则很难得出正确的答案.3 根据结构构造函数比较大小
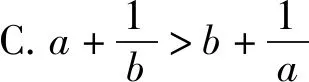



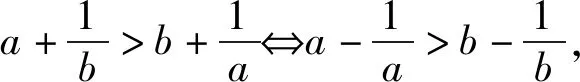
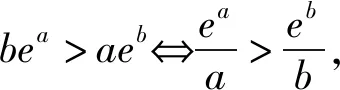



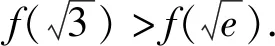
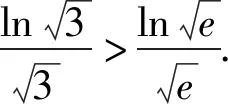
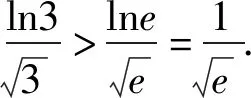




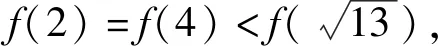
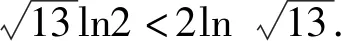







4 数形结合