基于时间序列迭代的输电线路覆冰厚度估计方法

(1. 国网四川省电力公司电力科学研究院，四川 成都 610041；2. 国网四川省电力公司营销服务中心，四川 成都 610041；3. 电子科技大学航空航天学院，四川 成都 611731；4. 电子科技大学信息与通信工程学院，四川 成都 611731)

0 引 言

在中国许多地区的输电线路都存在覆冰威胁[1]，特别是进入冬季之后，严重时最大覆冰厚度超过了80 mm[2]。输电线路覆冰问题如果没得到及时处理，会造成线路过荷载、输电线路断线、大面积闪络、电力设备损坏、杆塔倒塌等严重危害供电安全的问题[3]。每年由于线路覆冰导致的停电事故约占停电事故的四分之一，造成了巨大的经济损失[4—6]。

由于电网覆冰故障具有影响范围广、影响时间长、修复难度大等特点，其造成的损失已超过其他种类的自然灾害。有鉴于此，国内对电网冰灾做了大量的研究工作，在输电线路覆冰预测及防治领域取得很多重要成果。文献[7]基于架空输电线路轴向张力、二维倾角和风速风向、温度湿度等信息监测线路稳态覆冰状况，现场安装和运行情况证明了力学模型的有效性。文献[8]以绝缘子串悬挂点拉力和倾斜角为基本参量，考虑风偏因素，将导线力学参量归算到风偏平面，并通过风偏平面内竖直方向上的静力学受力平衡计算覆冰厚度的力学计算模型。文献[9]对直线杆塔两侧导线的覆冰厚度称重法力学模型进行了改进。文献[10]验证了直线塔覆冰厚度计算模型运用到线路地线上的有效性。文献[11]提出了一种等值覆冰厚度计算方法，且效果良好。

目前的大部分覆冰厚度计算模型复杂度高，参数量多,计算麻烦且普遍适用性有待提升。鉴于输电线路覆冰厚度获得方法仍有较大改进空间，下面提出一种基于时间序列迭代的输电线路覆冰厚度估计方法，并运用Python设计仿真实验以验证该方法的覆冰厚度计算准确性及其在拉力传感器承受导线长度变化情况下的科学性。

1 覆冰厚度计算方法

覆冰发生时拉力传感器会承受左右两侧部分电缆线及覆冰的重量，输电线路覆冰情况如图1所示。 悬垂绝缘子串左右两侧承受的导线长度分别为LLeft和LRight，总长度为L。

L=LLeft+LRight

(1)

图1 输电线路覆冰示意

悬垂绝缘子串的拉力分解情况如图2所示，拉力传感器垂直方向的分力为F×cosθ。

在下面的陈述中，对各参数进行如下定义：F为拉力传感器的拉力值；θ为绝缘子串的风偏角；L为拉力传感器承受的左右两侧导线的总长度；R为导线及覆冰的总半径；σ为导线及覆冰的等效线密度(即把覆冰和线路看为一个整体)；ρ为覆冰密度；g为重力加速度；下标0表示没有覆冰的初始时刻，下标n、n-1表示覆冰发生之后的第n个或n-1个时刻，即该物理量为对应参数在该时刻的值。

图2 悬垂绝缘子串的拉力分解

在覆冰发生后，依据t1、t2…tn时间顺序，多次收集拉力传感器的拉力值，例如间隔5 min或10 min，或根据覆冰增加趋势，动态调整测试间隔周期。随着拉力的增加，每次测量的覆冰厚度会增大。从n-1时刻到n时刻，覆冰厚度的增大值为Dn，如图3所示。

图3 输电线路覆冰后的横截面时序变化

在覆冰发生的n时刻，一方面，覆冰及导线的重力等于拉力传感器在垂直方向的分力；另一方面，覆冰及导线的重力等于n时刻新增加的冰重加上n-1时刻的导线及覆冰重量。考虑由于各种因素导致的相邻时刻L的变化，故覆冰线路的力学模型为

(Ln-1+ΔLn)+σn-1×(Ln-1+ΔLn)×g

(2)

在n-1时刻，覆冰及导线的重力等于拉力值的垂直分量，同时也等于“覆冰+线路”的等效密度与线路长度和g相乘，即

Fn-1×cosθn-1=σn-1×Ln-1×g

(3)

由式(2)和式(3)作差可以得到n时刻的前后时刻拉力变化量ΔFn。

ΔFn=Fn×cosθn-Fn-1×cosθn-1=

(Ln-1+ΔLn)+σn-1×(Ln-1+ΔLn)×g-

σn-1×Ln-1×g

(4)

由于相邻时刻时间间隔短，拉力传感器承受的导线长度L变化不大，甚至可以忽略，故可假设ΔLn≈0，前后时刻拉力变化量ΔFn为

(5)

在式(5)中只要确定了Ln-1即可求解出第n时刻覆冰厚度的增量Dn，但L在实际工程应用中很难准确测量。分析发现，可由式(5)和式(3)相比消去Ln-1，得到

在该铁路桥连续梁的施工过程中，温差和挂篮是该连续梁桥施工中的难点。温差对于连续桥梁的影响，通常突出体现在其能够影响桥梁内部结构，从而导致桥梁出现变形现象。连续梁施工过程中，由于箱梁顶面与底面散热较快，导致温度下降较快，而连续箱梁内部由于空气不流通，散热速度慢，温度也相对较高，导致连续箱梁内外部温度差较大，箱内因温度过高而发生膨胀，箱外因温度过低而发生收缩，最终导致连续梁变形。

(6)

通过等式基本运算，即可由式(6)求解出Dn的值。

(7)

当n=1，2，3，…N(N为计算终止时刻)时，测量对应时刻的拉力值与风偏角，根据式(7)即可求解到所有时刻的Dn。再将所有时刻的Dn累加可得覆冰总厚度D为

D=D1+D2+……+Dn

(8)

基于时间序列迭代的输电线路覆冰厚度估计方法具有严谨的数学推导，利用较少且易获得的参数(各时刻悬垂绝缘子串的拉力、悬垂绝缘子串的风偏角以及导线的初始线密度和半径)，即可建立一个效果良好的覆冰厚度模型，具有较好的普遍适用性和准确性。所提出的基于时间序列迭代的输电线路覆冰厚度估计方法的算法步骤如图4所示。

图4 算法步骤流程

2 覆冰厚度的仿真模型设计

线路覆冰是一个受多因素影响的复杂问题，且很多因素很难去测定，各种因素的变化又对覆冰厚度计算模型的准确度有一定的影响。在现有的力学模型估计覆冰厚度的方法中，一般设定拉力传感器所承受的导线长度L不变；但在实际的情况中，受风雪及覆冰情况的影响，L会有变化，这将导致线路覆冰厚度计算出现偏差。为了研究L变化对覆冰厚度计算模型准确度的影响，进行了如下仿真模型的设计。

2.1 输电线路导线参数

为了研究覆冰厚度计算方法的准确性，选择常见的导线型号LGJX-400/50，参数如表1所示，根据此导线参数利用Python进行仿真。

表1 导线LGJX-400/50参数

2.2 考虑L变化时的覆冰厚度真值计算模型

在未覆冰时，拉力传感器的值为F0，L为L0。为控制变量假设悬垂绝缘子串的风偏角θ保持不变，根据文献[10]可知风偏角θ的变化几乎为0，可以忽略。在覆冰发生的第i时刻，拉力传感器的值为Fi，L为Li，覆冰厚度为D。因为增加的覆冰重力与拉力传感器的增大值相等，故可得

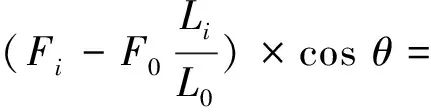
(9)

2.3 考虑L变化的基于时间序列迭代的覆冰厚度估计方法

在不忽略L变化的情况下，原方法中相邻时刻的覆冰厚度增加量Dn的计算公式变为

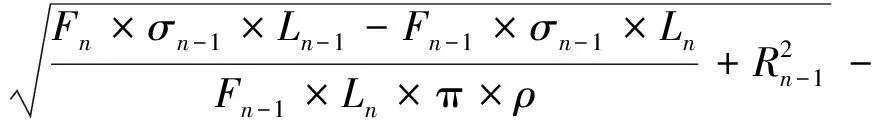
(10)

2.4 考虑L变化的等值覆冰厚度获得方法

在文献[11]中提出了一种输电线路等值覆冰厚度获得方法，通过测量输电线路覆冰前对悬垂绝缘子串的拉力、输电线路覆冰后对悬垂绝缘子串的拉力以及悬垂绝缘子串的风偏角，可以得到输电线路等值覆冰厚度Di为

(11)

考虑L变化后等值覆冰厚度Di为

(12)

3 覆冰厚度计算方法的仿真分析

根据表1中的导线参数，为控制变量设定θ为0，忽略风偏角影响，假定覆冰密度ρ为900 kg/m3，重力加速度g为9.8 N/kg，相邻杆塔间的输电导线长度为100 m，初始状态未覆冰时拉力传感器承受的左右两边导线长度之和L为100 m。输电线路的覆冰厚度取值一般为10 mm或15 mm[12]，为了数据更具有识别度，设定仿真覆冰厚度从0增加到50 mm。为验证基于时间序列迭代的输电线路覆冰厚度估计方法的准确性和科学性，在覆冰的过程中设置了4种不同的L变化场景：1)持续增加；2)先增加后减少；3)持续减少；4)先减少后增加。

3.1 L持续增加的场景

设定各时刻的覆冰厚度D分别为0、10 mm、20 mm、30 mm、40 mm、50 mm；设定各时刻L的值依次为100 m、102 m、104 m、106 m、108 m、110 m。根据式(6)可获得各时刻的拉力值F如表2所示。

表2 L持续增加场景下的拉力真值仿真结果

由表2可知，随着覆冰厚度D和拉力传感器承受导线长度L的增加，拉力值F在不断增大。根据获取的F值，按照提出的基于时间序列迭代的输电线路覆冰厚度估计方法(以下简称“迭代法”)计算覆冰厚度值DX，并得到相对误差ex=(DX-D)/D，结果如表3所示。

表3 L持续增加场景下的迭代法估计值仿真结果

考虑L的变化时，根据式(7)和式(9)可以得到该迭代法和文献[11]提出的输电线路等值覆冰厚度获得方法(以下简称“等值法”)的覆冰厚度计算结果DX与DY以及误差ex与ey，结果如表4所示。

表4 L持续增加场景下考虑L变化的仿真结果

从以上仿真结果可知，随着覆冰厚度的增加，在L持续增加的情况下，该迭代法的绝对误差和相对误差均有所增加，这主要是因为在未考虑L变化的情况下，由L的持续增加引起的误差变大。考虑L变化的情况下，迭代法和等值法的误差都明显减小，迭代法的相对误差接近于0。计算过程中取整或保留小数是造成误差的原因，等值法的绝对误差在持续增大但变化不大，其相对误差在持续减小。

3.2 L先增后减的场景

设定各时刻的覆冰厚度D分别为0、10 mm、20 mm、30 mm、40 mm、50 mm；设定各时刻L的值依次为100 m、102 m、104 m、102 m、100 m、98 m。覆冰开始后，L先增后减场景下的拉力真值仿真结果如表5所示；L先增后减场景下的迭代法估计值仿真结果如表6所示；L先增后减场景下考虑L变化的仿真结果如表7所示。

表5 L先增后减场景下的拉力真值仿真结果

表6 L先增后减场景下的迭代法估计值仿真结果

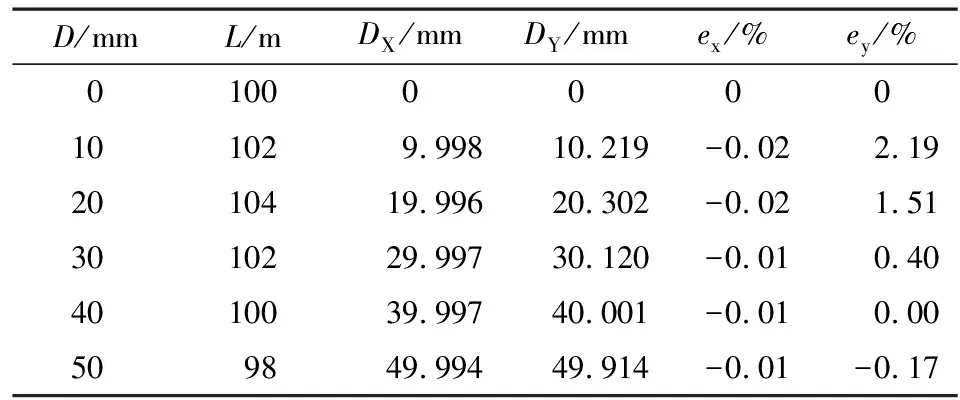
表7 L先增后减场景下考虑L变化的仿真结果

从仿真结果可知，随着覆冰厚度的增加，在L先增后减的情况下，当L减少时，F的增加量没有在L持续增加时大；该迭代法的绝对误差和相对误差均是先增大再变小；相对误差在L变化最大时达到最大为4.32%，在L变化最小即L变回L0时相对误差仅为-0.01%。考虑L变化的情况下，迭代法和等值法的误差都较小，迭代法的绝对误差接近0，等值法的绝对误差从2.19%减少至-0.17%。

3.3 L持续减少的场景

设定各时刻的覆冰厚度D分别为0、10 mm、20 mm、30 mm、40 mm、50 mm；设定各时刻L的值依次为100 m、98 m、96 m、94 m、92 m、90 m。覆冰开始后，L持续减少场景下的拉力真值仿真结果如表8所示；L持续减少场景下的迭代法估计值仿真结果如表9所示；L持续减少场景下考虑L变化的仿真结果如表10所示。

表8 L持续减少场景下的拉力真值仿真结果

表9 L持续减少场景下的迭代法估计值仿真结果

表10 L持续减少场景下考虑L变化的仿真结果

从仿真结果可知，随着覆冰厚度的增加，在L持续减少的情况下，该迭代法的绝对误差和相对误差的绝对值均在增加，且其变化幅度比L持续增加时大。这主要是因为在未考虑L变化的情况下，L的持续减小引起该误差变大。考虑L变化的情况下，迭代法的绝对误差和相对误差仍接近于0，等值法的绝对误差为负数且在持续减小，其相对误差的绝对值也在变小。

3.4 L先减后增的场景

设定各时刻的覆冰厚度D分别为0、10 mm、20 mm、30 mm、40 mm、50 mm；设定各时刻L的值依次为100 m、98 m、96 m、98 m、100 m、102m。覆冰开始后，L先减后增场景下的拉力真值仿真结果如表11所示；L先减后增场景下的迭代法估计值仿真结果如表12所示；L先减后增场景下考虑L变化的仿真结果如表13所示。

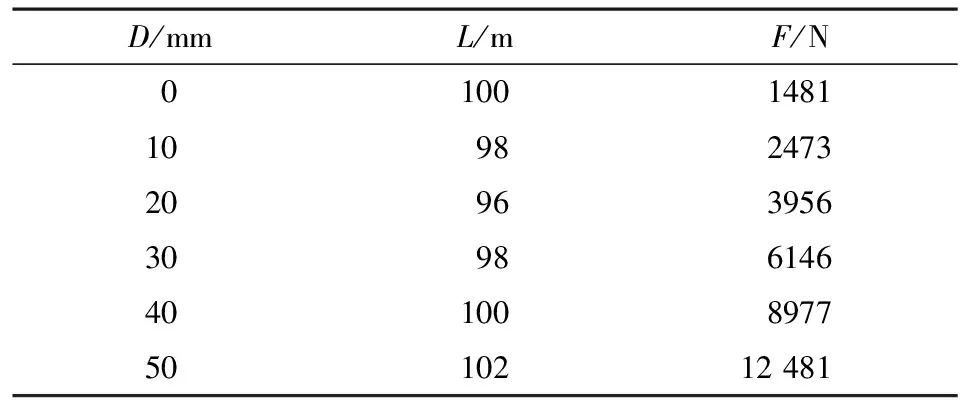
表11 L先减后增场景下的拉力真值仿真结果

表12 L先减后增场景下的迭代法估计值仿真结果

表13 L先减后增场景下考虑L变化的仿真结果

从以上仿真结果可知，随着覆冰厚度的增加，在L先减后增的情况下，与L先增后减的情况相反，该迭代法的绝对误差和相对误差先减小后增大，L越接近L0时相对误差的绝对值越小。考虑L变化的情况下，和前面场景类似，迭代法的效果优于等值法。

4 结 论

上面提出了一种基于时间序列迭代的输电线路覆冰厚度估计方法，并模拟在覆冰厚度逐渐增加的情况下，从拉力传感器承受的导线长度L持续增加、先增后减、持续减少和先减后增4种场景，验证了所提方法的有效性和科学性。结论如下：

1)在覆冰厚度小于20 mm时，在4种场景下该迭代法的相对误差的绝对值最大为4.46%，最大的绝对误差为0.892 mm；该误差在实际工程应用中影响不大，且能在L变化的影响下有效地估计覆冰厚度。在覆冰厚度超过20 mm时，该迭代法的最大相对误差绝对值为7.13%，优于现有的大多数力学方法，且在实际情况中覆冰超过20 mm的情况罕见。

2)在考虑L变化的情况下，该迭代法的表现优于目前先进的等值厚度计算方法，其未来应用空间将会更大。