多逆变器并网系统谐振混合阻尼参数设计

(四川水利职业技术学院电力工程学院，四川 崇州 611231)

0 引 言

为了实现“碳达峰、碳中和”目标，需要以风力发电、光伏发电为代表的可再生清洁能源替代传统化石能源[1]。高比例新能源并网必然需要多逆变器并网。具有良好滤波效果的LCL型滤波器被广泛用于新能源并网逆变器的输出滤波。该型滤波器自身存在谐振问题，同时多LCL型逆变器并网后还存在系统谐振问题。对于单台LCL型逆变器的谐振阻尼研究已经比较深入，取得了比较好的阻尼效果。然而，对于多LCL型逆变器并网系统谐振阻尼方法还在广泛研讨中。文献[2]通过对比仿真试验认为对于多逆变器谐振抑制而言，有源阻尼比无源阻尼更胜一筹。各种阻尼方法中被提及较多的方法有改进型有源阻尼法[3—6]、阻抗重塑法[7—10]和有源阻尼器[11—13]。改进型有源阻尼法不产生额外电能损耗，但是控制算法非常复杂。阻抗重塑法的实现需要陷波器与虚拟电阻配合，陷波器只能适应系统谐振频率非常小范围的波动；对于大型新能源电场中出现故障，需要调整电网结构因而改变系统阻抗的情况无法胜任。有源阻尼器将新增设备，增加投资，正在理论研究阶段，还未大规模投入使用。混合阻尼作为单台LCL型逆变器谐振抑制策略取得了良好效果[14—15]，并且电容支路串联无源阻尼电阻搭配电容支路电流反馈的混合阻尼策略研究的也比较成熟。因此，提出基于多台LCL型逆变器并网系统谐振抑制的混合阻尼参数设计，避免逆变器控制算法变得更加复杂，又不增加新的投资成本，符合工程经济需求。

1 单逆变器参数设计

1.1 电路拓扑

单逆变器电路拓扑如图1所示。图中：Udc为逆变器直流侧电压；S1—S4为电力电子器件；L1、C和L2组成LCL滤波器；Rd为LCL滤波器电容支流上无源阻尼电阻；Lg为电网等效电感；Hi1为电容支路反馈系数，即有源阻尼参数；Hi2为并网电流采集系数；Ug为电网电压；Gi(s)为电流控制器，采用准比例谐振(quasi proportional resonant,QPR)控制器，其表达式为

(1)

式中：Kp为比例系数；Kr为谐振系数；ωi为截止角频率；ω0为基波角频率。

1.2 参数设计

文献[16]对单台并网逆变器LCL滤波器参数、电容支路反馈系统和QPR控制器参数设计给出了具体的设计方法。其中，Hi1的取值约束条件如式(2)所示。

(2)

式中:fr为LCL滤波器谐振频率;fc为环路增益的截止频率;fSW为开关频率;PM为相位裕度;GM为环路增益的幅值裕度；Tfo为基波频率处环路增益的幅值；KPWM为调制系数。

图1 单台LCL型逆变器原理

对于阻尼电阻的取值，文献[17]以损耗为约束条件、滤波效果最好为目标，采用智能算法进行优化获取。文献[18]提出临界无源阻尼参数设计法，还给出了上述混合阻尼结构无源阻尼系数临界值为0.28。无源电阻Rd的计算式为

(3)

式中:ζPD为无源阻尼系数;ωr为LCL滤波器谐振角频率;C为LCL滤波器电容。

上述参数的取值是按研究人员的经验获得的，不一定是最优值。同时，参数取值的目的是保证单台逆变器并网稳定性和并网电能质量要求得到满足，对于多逆变器并网稳定性和并网电能质量而言，这些参数或许还有优化的空间。

2 多逆变器系统谐振机理

多逆变器并网的诺顿等效电路如图2所示。根据图1可以得到混合阻尼策略下单台LCL型逆变器的等效阻抗表达式，如式(4)。根据图2可以得到多逆变器并网时公共连接点(point of common coupling,PCC)的阻抗表达式，如式(5)；进而得到谐振时PCC点的阻抗表达式，如式(6)。由式(6)可得发生系统谐振时的谐振角频率表达式，如式(7)。

图2 诺顿等效电路

(4)

(5)

(6)

(7)

由式(7)可以看出，系统谐振只与LCL滤波器、电网等效电感有关，与电容支路串联电阻、有源阻尼参数无关。说明在仿真实验时，同一个系统谐振频率可以用于由不同串联电阻和有源阻尼参数组成的试验组进行试验。还有研究表明，多逆变器并联系统中存在多个谐振频率[19]，为了简化问题讨论难度，下面并不涉及多个并网谐振频率问题。

3 混合阻尼设计

3.1 动态电网阻抗下阻尼系数分析

文献[14]给出了单机逆变器并网无源阻尼和有源阻尼的阻尼系数ζPD、ζAD的表达式，如式(8)和式(9)所示。

(8)

(9)

由式(8)可知无源阻尼电阻Rd与无源阻尼系数ζPD成正比。无源阻尼系数ζPD与阻尼电阻Rd、电网等效电感Lg的关系如图3所示：随着电网等效电感Lg增加，无源阻尼系数ζPD将减小；不同无源电阻参数Rd对应无源阻尼系数ζPD的变化率不同，且随着电网等效电感增加而减小的变化率也不同。由式(9)可知有源阻尼参数Hi1与有源阻尼系数ζAD成正比。有源阻尼系数ζAD与有源阻尼参数Hi1、电网等效电感Lg的关系如图4所示：随着电网等效电感Lg增加，有源阻尼系数ζAD将减小；不同有源阻尼参数Hi1对应有源阻尼系数ζAD的变化率不同，且随着电网等效电感增加而减小的变化率也不同。

图3 ζPD、Rd、Lg的关系

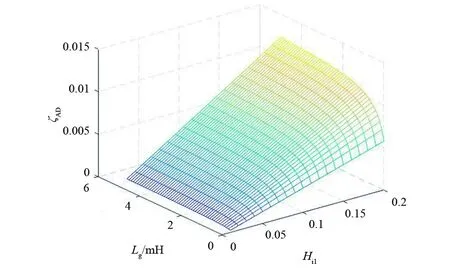
图4 ζAD、Hi1、Lg的关系

虽然，电网等效电感减小时阻尼系数将增大，但是电网等效电感增大时阻尼系数也将减小。在电网等效电感发生波动时，为了尽可能减小阻尼系数波动范围，阻尼系数变化率取值应尽可能小。将式(8)和式(9)对电网等效电感求微分得到电网等效电感发生变化时无源阻尼系数变化率kPD和有源阻尼系数变化率kAD。式(10)和式(11)说明无源阻尼系数变化率与无源阻尼电阻成正比，有源阻尼系数变化率与电容支路反馈系数成正比。因此，既要实现高阻尼系数，又要降低其对电网等效电感变化的波动，需要合理评估无源阻尼电阻参数和有源阻尼参数取值。

(10)

(11)

3.2 混合阻尼参数设计

混合阻尼的阻尼系数由无源阻尼系数和有源阻尼系数组成，如式(12)所示。

(12)

式(12)也说明无源阻尼和有源阻尼可以单独考虑。由于有源阻尼方法采用虚拟电阻技术，不会产生额外的能量损耗，单从阻尼系数的角度，电容支路反馈系数取值越大越好；但是，无源阻尼的阻尼电阻要产生电能损耗，它的取值还需进一步权衡，因此，先确定有源阻尼系数，再确定无源阻尼系数。混合阻尼参数的设计流程如图5所示。

针对图5中无源阻尼参数设计问题，文献[18]提出的临界无源电阻设计方法是针对单台逆变器并网的情况，无源电阻计算式中采用LCL滤波器谐振角频率无法体现多逆变器并网中并网逆变器数量带来的影响。多逆变器并网临界无源阻尼电阻的计算式可以采用式(8)，用系统谐振角频率替代LCL滤波器谐振角频率。阻尼系数并不是只针对谐振频率，采用并网电流总谐波率(total harmonic distortion,THD)与谐波系数(harmonic factor,HF)两个指标组成的综合电能质量指标，再考虑无源阻尼电阻损耗更符合混合阻尼在实际工程应用中的评价。

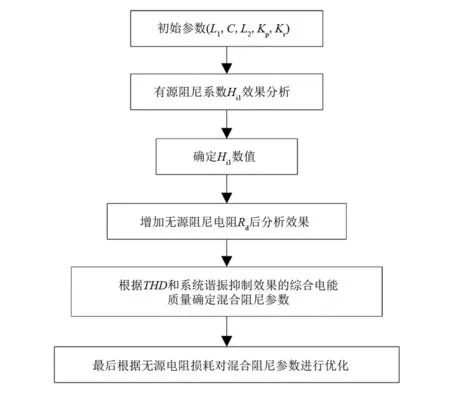
图5 混合阻尼参数设计流程

4 仿真实验研究

根据图1和图2在Matlab/Simulink上搭建3台LCL型逆变器并网仿真试验平台。逆变器参数如表1所示[16]。

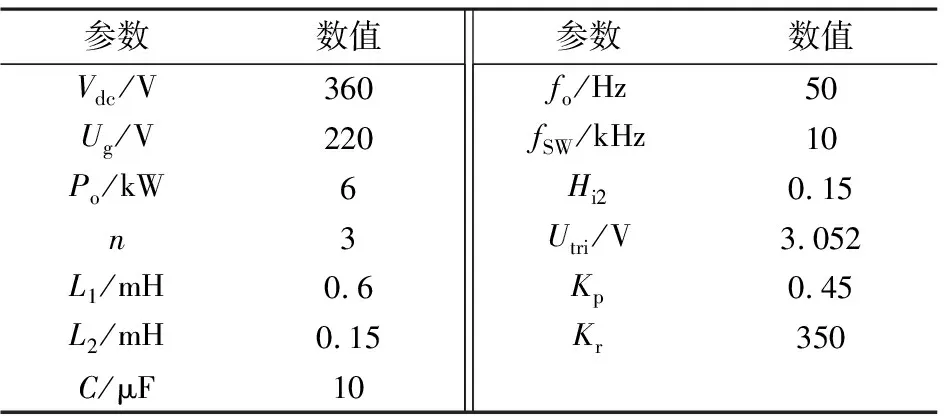
表1 逆变器参数

根据式(3)和式(8)分别计算单台逆变器并入弱电网可得无源阻尼电阻值约为2.0 Ω和2.6 Ω。根据式(8)计算3台逆变器并网无源阻尼电阻值约为3.2 Ω。在Hi1=0.1情况下电网等效电感Lg=0.2 mH的弱电网，没有电网背景谐波注入的并网电流幅频特性如图6所示。由图6可以看出，优化后临界无源阻尼电阻对于逆变器并入无背景谐波弱电网的阻尼效果要略微好一些。

对第一章内容中有源阻尼参数Hi1理论计算范围为0.009～0.200进行仿真验证后，确定其最小值为0.057才能保证逆变器稳定并网。进行8组仿真实验，Hi1取值分别为0.06、0.08、0.10、0.11、0.12、0.14、0.16、0.20。电网等效电感Lg=0.2 mH时，可计算系统谐振频率约为2758 Hz。仿真时，向系统注入3%基波幅值的2758 Hz谐波，得到如图7所示的仿真结果。从图7可以看出，各组有源阻尼参数对系统谐振都有抑制效果。Hi1数值越大，抑制效果越好，符合前述理论预期。但是综合THD和HF两个指标来看，Hi1=0.11是比较好的选择。

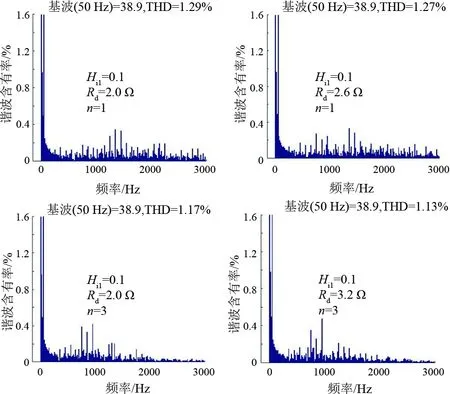
图6 无背景谐波下并网电流幅频特性

图7 各组有源阻尼参数下并网电流幅频特性

3台逆变器并网，注入3%基波幅值的2758 Hz谐波，串联无源阻尼电阻Rd分别取值0.5 Ω、1.0 Ω、1.5 Ω、2.0 Ω、2.5 Ω、3.0 Ω、3.2 Ω、3.5 Ω。仿真结果如图8所示。由图8可知，无源阻尼电阻越大，系统谐振抑制效果越好。优化后的临界无源阻尼电阻比优化前取得了更好的抑制效果。根据THD和系统谐振抑制效果的综合电能质量确定混合阻尼参数为Hi1=0.11，Rd=3.2 Ω。但是无源阻尼电阻值越小，损耗越小。从图9可以看出Rd=1.5 Ω为最优参数。

图8 各组新增无源阻尼参数下并网电流幅频特性

为了验证所设计的混合阻尼参数对电网等效电感发生变化时的抑制效果，再进行3组对比试验，试验结果如图10所示。除了所提方法设计的参数外，另一组参数来源于文献[15]所述方法。该方法要求无源阻尼电阻尽可能数值取小一点，有源阻尼参数Hi1尽可能取大一点，因此Rd=1 Ω，Hi1=0.2。第一组参数Lg=0.2 mH，谐振频率约为2758 Hz；第二组参数Lg=1 mH，谐振频率约为2242 Hz；第三组参数Lg=2 mH，谐振频率约为1950 Hz。图10显示，对于第一组试验，两种设计方法所得参数抑制效果相当，而对于第二组和第三组试验，所提方法设计的参数对系统高频谐振和低频谐波取得了更好的抑制效果。

图9 HF与Rd的关系

图10 不同Lg混合阻尼效果

注入电网背景谐波(频率2758 Hz，3%基波辐值)，在0.08 s时刻阻尼策略从无源阻尼(Rd=1.5 Ω)切换到所提混合阻尼(Rd=1.5 Ω，Hi1=1.1)，得到的并网电流波形如图11所示。该图显示所提混合阻尼对系统谐振抑制效果明显。同时，在阻尼策略切换过程中，逆变器并网稳定性和动态效果较好。

图11 并网电流波形

5 结 论

上面提出了一种基于多逆变器并网谐振抑制的混合阻尼设计方法，该方法根据无源阻尼系数和有源阻尼系数的特性先后确立有源阻尼参数和无源阻尼参数。相对单台逆变器而言，该方法可看作混合阻尼参数优化，避免增加逆变器控制复杂度。无需新增设备也有利于降低新能源发电成本。仿真实验结果表明用所提方法设计混合阻尼参数可以较好地抑制多逆变器系统谐振，并且对系统阻抗变化也具有良好的适应性。所提方法的特点总结如下：

1)相同阻尼效果条件下，所提方法降低了无源阻尼电阻的阻值，减小了电能损耗，为多逆变器并网无源阻尼电阻参数设计提供了理论依据；

2)相比有源阻尼，所提方法不仅优化了THD，还进一步降低了HF，取得了更好的综合抑制效果；

3)所提方法设计的混合阻尼参数可以良好地适应多逆变器并网阻抗动态变化，为解决系统局部故障、新建或改建系统谐振抑制方面提供了新思路。